Система линейных алгебраических уравнений
Рассмотрим систему линейных алгебраических уравнений
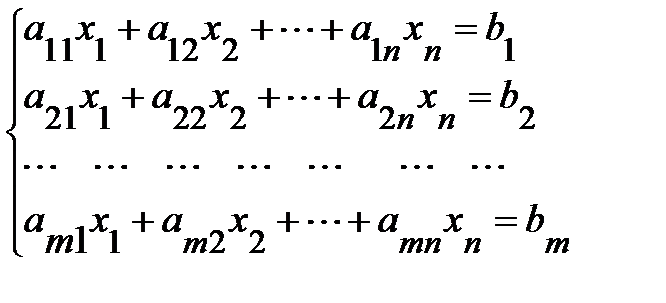, (1)
где а i j – числовые коэффициенты системы; b i - произвольные числовые константы, называемые свободными членами системы; х 1, х 2 ,…,х n – неизвестные величины, подлежащие определению.
Вводя матрицы А =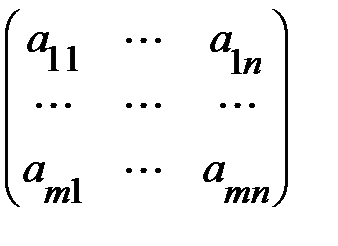 
; х = 
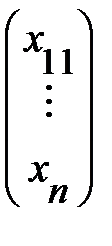; b =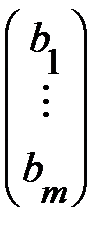 
,
систему (1) можно записать в матричном виде
Ах = b. (2)
Матрица А называется основной матрицей системы (1), а матрица
В =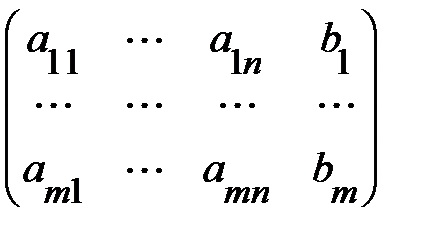 
называется расширенной матрицей системы (1).
Система (1), в которой число неизвестных n совпадает с числом m уравнений, называется крамеровской системой линейных уравнений:
m = n
Ax = b . (3)
В этом случае матрица А является квадратной матрицей n –го порядка.
Если определитель матрицы А в системе (3) отличен от нуля, то умножая матричное уравнение слева на обратную матрицу А-1, получим его решение
А - 1 Ах = А - 1 b Þ Ex = x = А - 1 b. (4)
Пример 16. Решить систему матричным методом
ì х1 + 2х2 – х3 = 8
í 2х1 – х2 + х3 = -3
î 3х1 + х2 – 2х3 = 11 .
Решение. Имеем матрицы
А =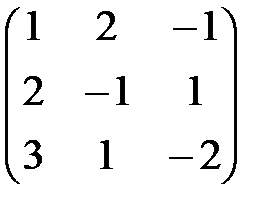 
; х = 
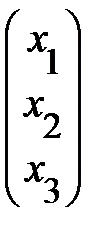; b =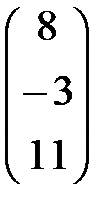 
.
Для применения формулы (4) необходимо вычислить обратную матрицу А - 1 (результат получен в примере 13). Окончательно получим
x = А - 1 b=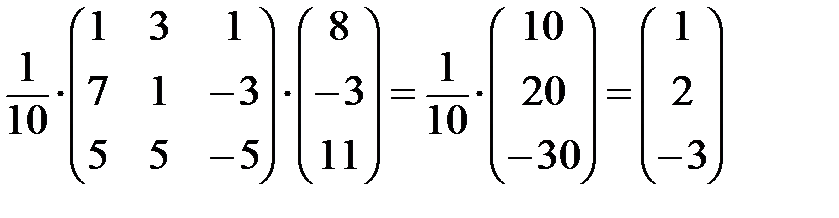 
, т.е.
х 1 = 1; х 2 = 2; х 3 = -3.
Если число неизвестных величин в системе (3) невелико, то для получения решения можно воспользоваться формулами Крамера
Х i = 
(5)
"i = 1, 2,…, n.
Пример 17. Решить систему по формулам Крамера
.
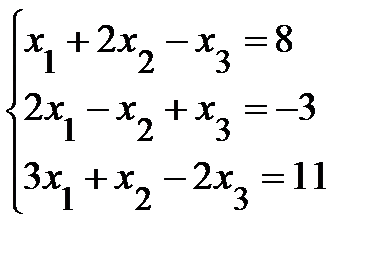Решение. Найдем определители:
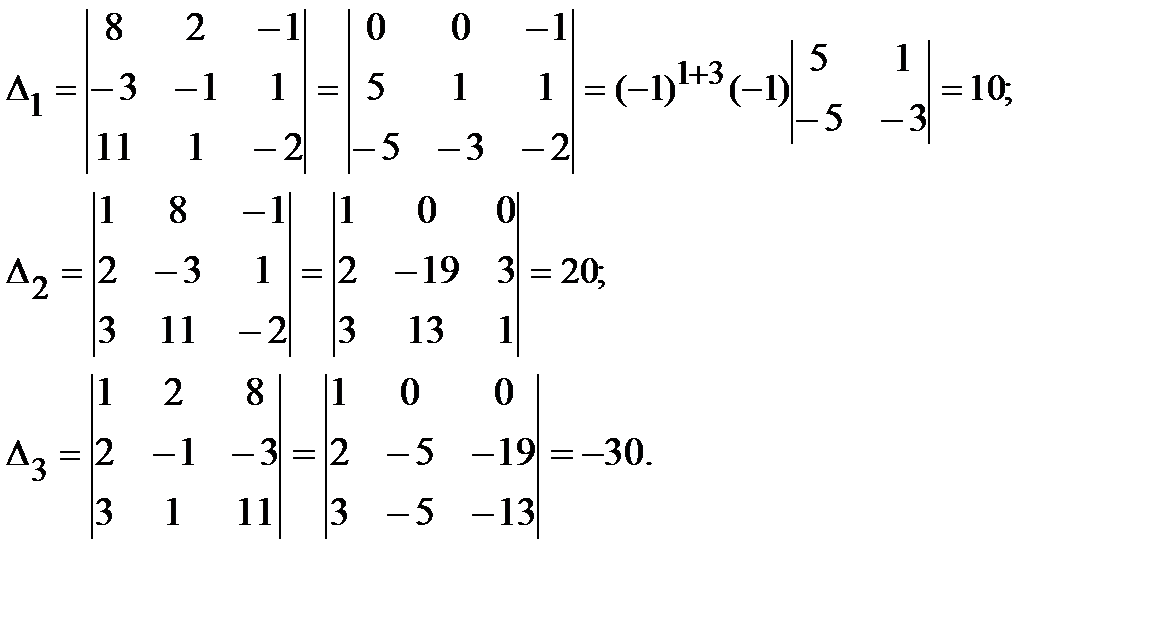
Определитель матрицы A вычислен нами ранее и равен D = det A = 10.
Применяя формулы Крамера (5), найдем решения системы:
х1=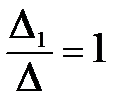 
; х 2 = 
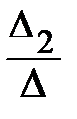= 2 ; х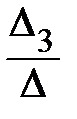3 = 
= -3.
Перейдем к решению систем линейных уравнений, заданных в общем виде (1), когда число n неизвестных величин х i i = 1,2, …, n необязательно совпадает с числом m уравнений системы.
Система линейных уравнений (1) называется однородной, если все её правые части равны нулю: b 1 = b 2 = …= b m = 0. В противном случае система (1) называется неоднородной.
Решением системы (1) называется набор таких чисел х 1 , х 2 , …, х n, которые обращают каждое уравнение системы в числовое тождество.
Если система (1) имеет хотя бы одно решение, то она называется совместной. Система, не имеющая ни одного решения, называется несовместной.
В частности, любая однородная система всегда совместна, так как одним из ее решений является нулевое (тривиальное) решение:
х 1 = х 2 = …= х n = 0.
Теорема Кронекера – Капелли
Система (1) линейных уравнений совместна тогда и только тогда, когда ранг основной матрицы r ( A ) равен рангу расширенной матрицы r ( B ):
r ( A ) = r ( B ) .
Если r ( A ) < r ( B ), то система (1) несовместна.
Если r ( A ) = r ( B ) = n (где n – число неизвестных), то система (1) имеет единственное решение.
Если r ( A ) = r ( B ) < n, то система (1) имеет бесчисленное множество решений.
Система, имеющая единственное решение, называется определенной; в противном случае система называется неопределенной.
Общий способ решения системы основан на последовательном преобразовании исходной системы к такой эквивалентной системе, для которой решения находятся достаточно просто. При этом с расширенной матрицей системы производятся действия, приводящие её к ступенчатому виду. Метод решения систем линейных уравнений таким способом называется методом Гаусса.
Пример 18 . Найти общее решение системы
.
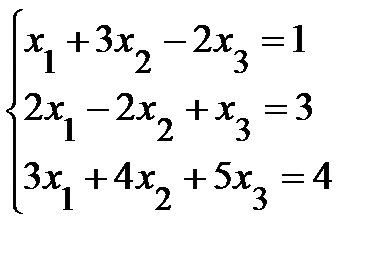Решение. Запишем расширенную матрицу и приведем ее к ступенчатому виду с помощью элементарных преобразований:
В =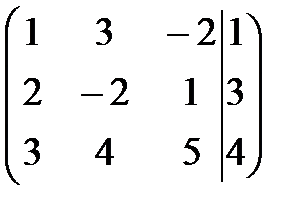 
~ 
~ 
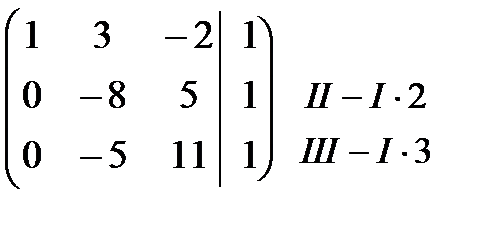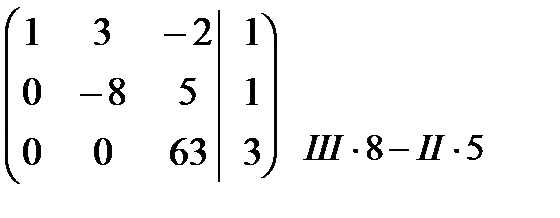= В 1.
Получим ранги r(А) = r(В 1) = 3, причем это число совпало с числом неизвестных n= 3 в данной системе. Это означает, что система имеет единственное решение. Для его нахождения запишем систему, эквивалентную данной:
.
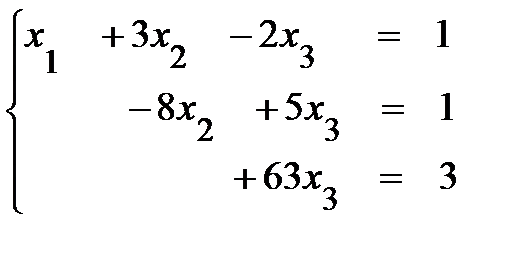Методом подстановки найдем решение этой системы:
х 1 =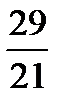 
; х 2 = 
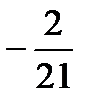; х 3 = 
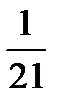; или Х = 
.
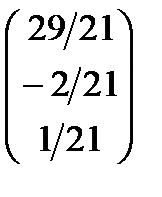Пример 19 . Найти общее решение системы уравнений
.
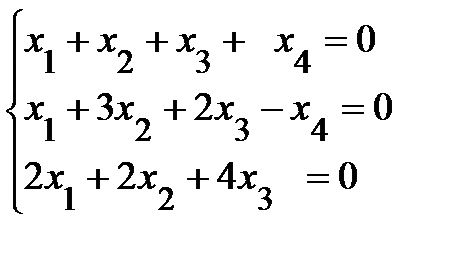Решение. Приведем матрицу однородной системы к ступенчатому виду
А =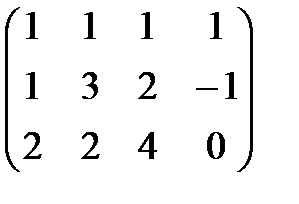 
~ 
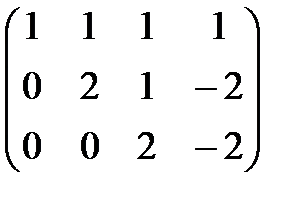= А1 .
Ранг эквивалентной матрицы А1 равен r (А 1) = 3, при этом число переменных n = 4 (замечаем, что n > r (А 1)). В этом случае какие-либо три переменные, например, х 1 , х 2 и х 3, будем называть базисными, а оставшиеся переменные, в данном случае это х 4 , будем называть свободными.
Запишем систему, эквивалентную данной
.
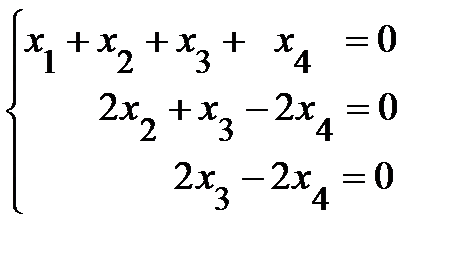Перенесем переменную х 4 в правую часть и получим
.
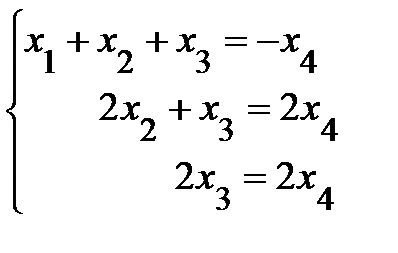Запишем основную А и расширенную В матрицы этой системы
А =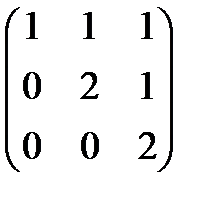 
; В =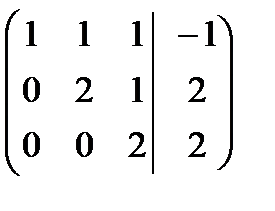 
.
Ранги этих матриц равны r (А) = r (В) = 3, причем n = 4 > r (А) = 3, поэтому система является неопределенной и имеет бесчисленное множество решений. Обозначим х 4= t и выразим базисные переменные
х 1=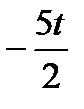 
; х 2= 
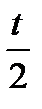; х 3 = t .
Общее решение исходной системы будет Х =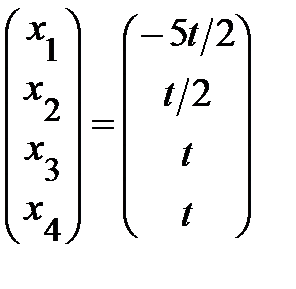 
.
При фиксированном значении t = t 0( t 0 – числовое значение) из общего решения можно выделить некоторое частное решение системы
Х 0 =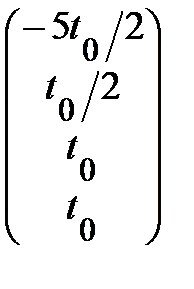 
.
Вопросы для самопроверки
1. Запишите систему линейных уравнений в развернутом и матричном виде.
2. Какая система называется крамеровской системой линейных уравнений?
3. Сформулируйте правило Крамера решения систем линейных уравнений.
4. Сформулируйте правило решения систем линейных уравнений матричным методом.
5. Какие преобразования матрицы называются эквивалентными?
6. Какие системы называются совместными?
7. Сформулируйте теорему Кронекера-Капелли.
8. Какие системы называются определенными (неопределенными)?
9. В чем заключается метод Гаусса решения систем линейных уравнений?
10. Что такое матрицы линейного преобразования?
11. Запишите линейное преобразование в матричной форме.
12. Запишите в матричной форме нахождение преобразования, обратного данному линейному преобразованию.
ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
Векторы и действия над ними
Следует различать два типа объектов, встречающихся в естествознании: скалярные и векторные величины.
Скалярные величины – это величины, которые характеризуются числовым значением. Например, скалярными величинами являются масса тела, давление, коэффициент трения и т.д.
Векторные величины – это величины, которые кроме числового значения характеризуются еще направлением. Примерами таких величин являются: скорость тела, сила, действующая на тело, импульс тела и т.д.
Вектором называется направленный отрезок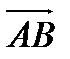 
с начальной точкой А и конечной точкой В, который можно перемещать параллельно самому себе.
Длиной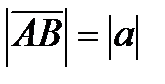 
вектора 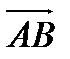= а называется число (неотрицательное), равное длине отрезка АВ, соединяющего точки А и В.
Нулевой вектор – вектор, начальная и конечная точки которого совпадают: =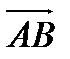 
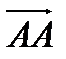= О . Его длина равна нулю ( |О| = 0 ), а направление для него не имеет смысла.
Единичный вектор е - вектор, длина которого равна 1 ( |е| = 1). 
Коллинеарные векторы – векторы, лежащие на одной прямой или на параллельных прямых. Векторы а , b и c , изображенные на рис. 1, коллинеарны.
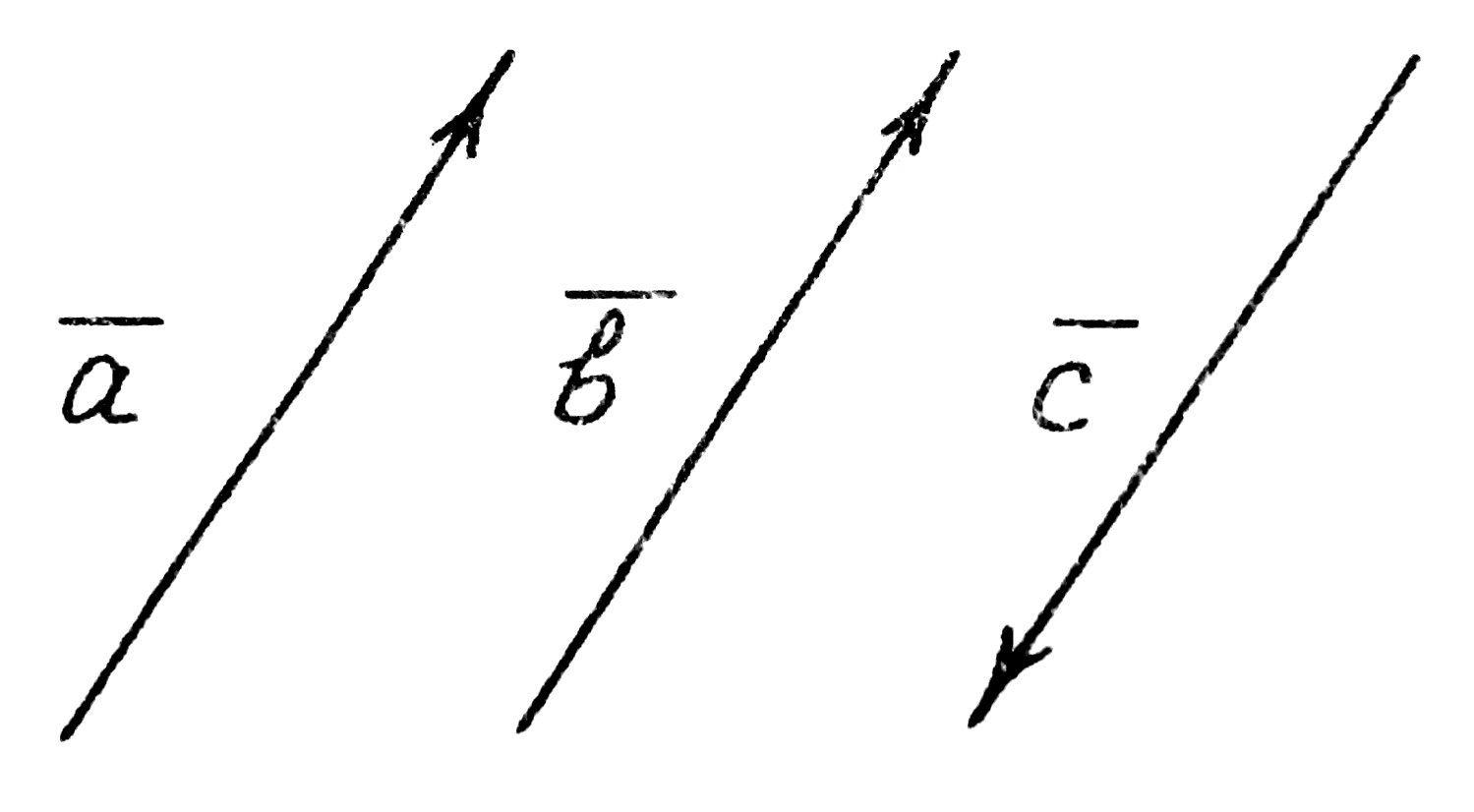
Рис. 1
Компланарные векторы – векторы, которые лежат в одной плоскости или в параллельных плоскостях.
Равные векторы – векторы, которые коллинеарны, имеют одинаковую длину и одинаковое направление.
Суммой а + b векторов а и b называется вектор, идущий из начала вектора а в конец вектора b, если начало вектора b совпадает с концом вектора а (т.е. вектор b приложен к вектору а) – это правило треугольника (рис. 2).
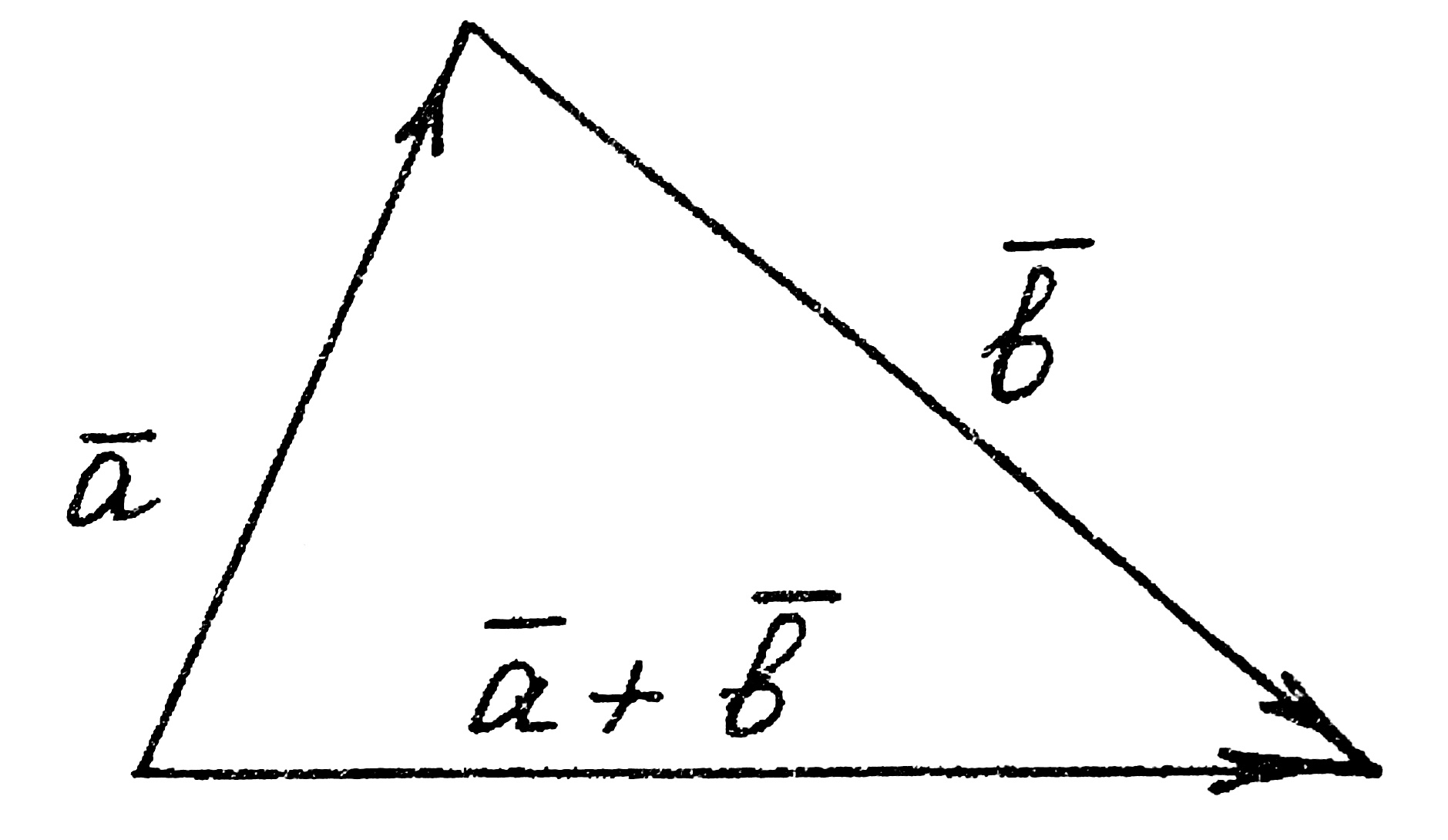
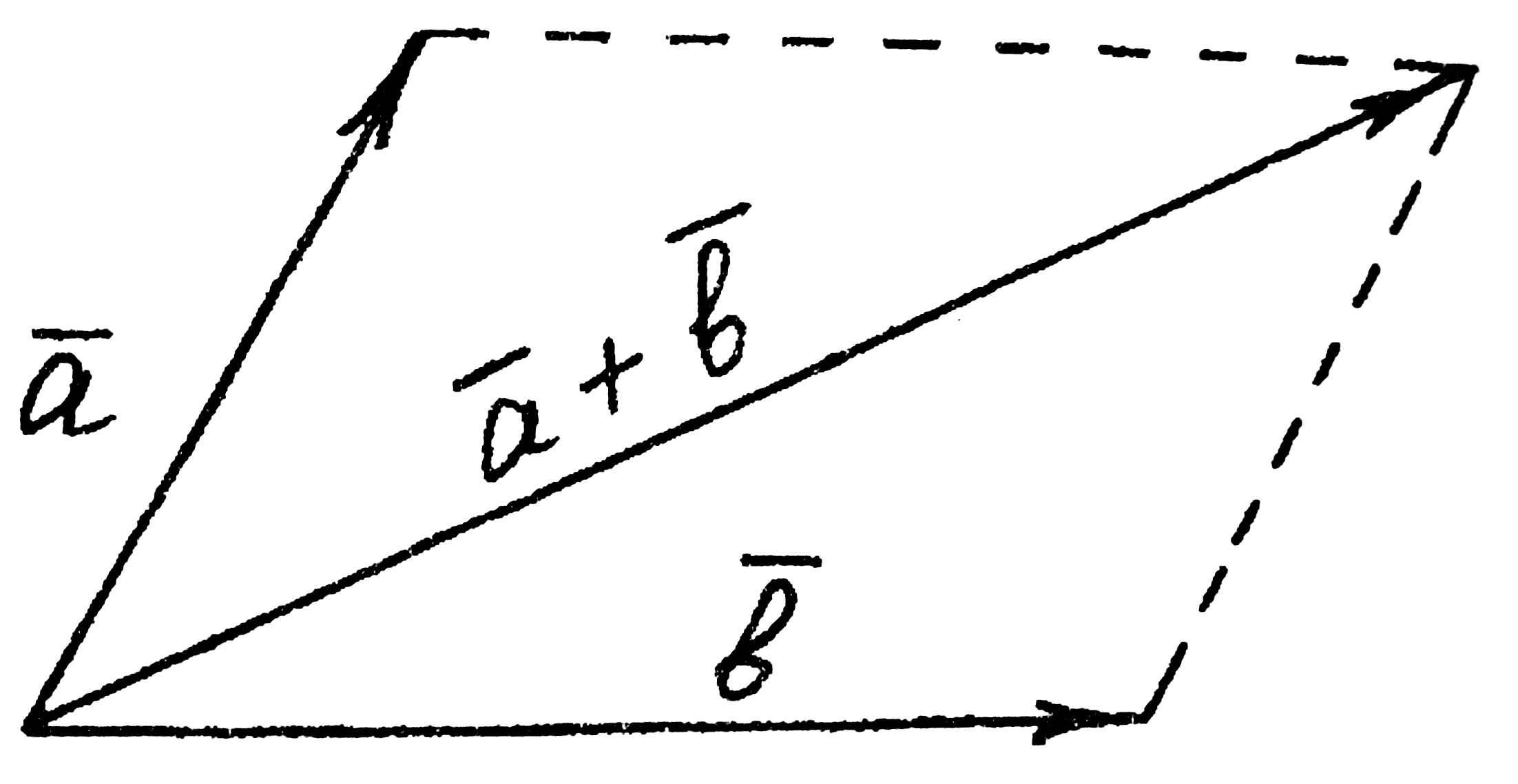
Рис. 2 Рис. 3
Если векторы а и b имеют общее начало и на них как на сторонах построен параллелограмм, то суммой а + b будет диагональ параллелограмма.
Правило вычитания векторов показано на рис. 3 .
Произведением lа (или аl) вектора а на действительное число l называется вектор b, коллинеарный вектору а, длина которого |lа½= |l|×|а|, а направление совпадает с вектором а , если l > 0 , или противоположно а, если l < 0.
Проекцией точки А на прямую l называется точка А*, в которой пересекается прямая l с плоскостью, перпендикулярной к l, проходящей через точку А (рис. 4).
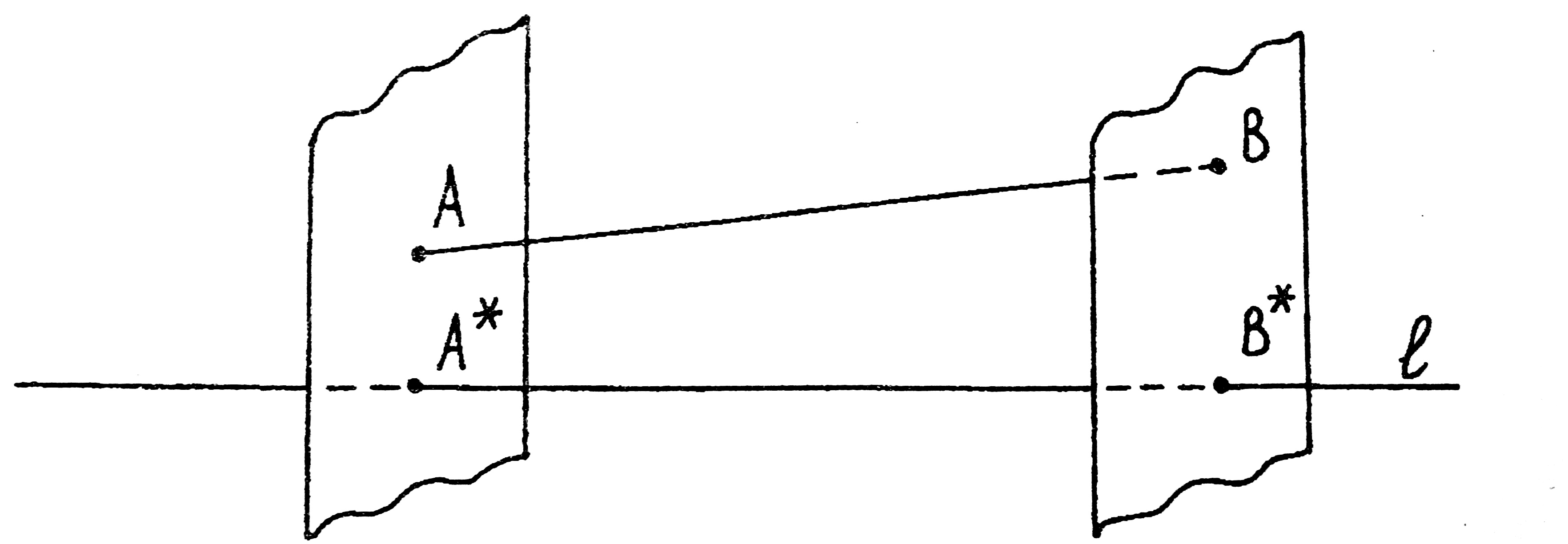
Рис. 4
Проекцией вектора а = 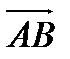(рис. 4) на направленную прямую l называется вектор 
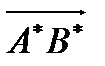, где А*и В* соответственно проекции точек А, В на прямую l.
Проекция вектора а = 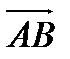на направленную прямую l будем обозначать символом 
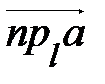(прlа ) .
Числовой проекцией |прlа| вектора а на направленную прямую l называется произведение длины вектора а на косинус угла a между вектором а и прямой l
|прlа| = |а|×cos ( а,l ) = |а|×cosa ( 0 £a£p ).
2. Линейное пространство. Линейная зависимость. Базис
Линейным пространством L называется множество элементов, для которых определены операции сложения двух векторов и умножения вектора на число, обладающие следующими свойствами
1. Для любых векторов а и b из линейного пространства
а + b = b + а (коммутативность сложения).
В символьной записи это свойство будет иметь вид
" a, b Î L Þ а + b = b + а .
2. " a, b ,с Î L Þ( а + b) + с = а + ( b + c) ( ассоциативность).
3. $ О Î L : " a Î L Þ а + О = а (существование нулевого вектора).
4. " a Î L $ (- а) Î L (противоположный вектор) : а + (-а) = О.
5. " l Î R, " a, b Î L Þ l (а + b ) = lа +lb.
6. " l 1, l 2 Î R , " a Î L Þ ( l 1 + l 2) а = l 1а + l 2а .
7. " l 1, l 2 Î R , " a Î L Þ ( l 1×l 2) а = l 1(l 2 а ).
8. " a Î L Þ 1×а = а .
Линейными пространствами, в частности, являются: множество действительных чисел; множество векторов на плоскости или в пространстве; множество всех функций, определенных на каком-нибудь отрезке и т.д.
Определение 21. Линейной комбинацией векторов а1, а2, …, аn называется
сумма с1 а1 + с2а2 + …+ сnаn, где коэффициенты
с1, с2, …, сn– действительные числа.
Определение 22. Совокупность векторов а1, а2, …, аn линейного
пространства называется линейной зависимой, если их
линейная комбинация равна нулю
с1 а1 + с2 а2 + …+ сn аn = 0
и при этом хотя бы один из коэффициентов с1, с2, …, сn
отличен от нуля.
Определение 23. Совокупность векторов а1, а2, …, аn называется
линейно независимой, если равенство
с1 а1 + с2 а2 + …+ сn аn= 0
выполняется лишь в случае, когда все коэффициенты
с1, с2, …, сn равны нулю.
Утверждение 1. Необходимым и достаточным условием линейной зависимости двух векторов на плоскости является их коллинеарность.
Утверждение 2. Необходимым и достаточным условием линейной зависимости трех векторов в пространстве является их компланарность.
Определение 24. Базисом в линейном пространстве L называется
упорядоченная система А ( А = { а1, а2, …, аn })
максимально возможного числа векторов {а1, а2, …, аn},
удовлетворяющая условиям:
1) совокупность векторов а1, а2, …, аn линейно независима;
2) любой вектор a Î L в системе векторов А единственным
образом представляется в виде их линейной комбинации
а = х1 а1 + х2 а2 + …+ хn аn.
Числа ( х1, х2, …, хn ) называются координатами вектора а в базисе
{ а1, а2, …, аn }.
Размерность линейного пространства L определяется максимальным числом n линейно независимых векторов и обозначается dim L (dim L = n ). Если это число конечно, то такое пространство L называется конечномерным.
Любая пара неколлинеарных векторов а1, а2 на плоскости является базисом множества всех векторов, лежащих на плоскости.
Любая тройка некомпланарных векторов а1, а2, а3 в трехмерном пространстве является базисом множества всех векторов, лежащих в этом пространстве.
В случае декартовой прямоугольной
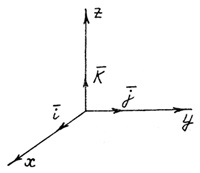системы координат в трехмерном
пространстве в качестве базисных выбирают
единичные векторы
i = (1,0,0), j = (0,1,0), k = (0,0,1) ,
которые:
а) линейно независимы;
б) имеют длину, равную единице, т.е. |i| = |j| = |k| = 1;
c) по направлению совпадают с направлением осей
Рис. 5 координат OX , OY , OZ.
Векторы i, j ,k называются ортами и образуют базис.
Любой произвольный вектор а в этом трехмерном базисе может быть представлен в виде линейной комбинации а = х i + у j + z k или а = ( х, у, z ), где х, у, z - координаты ветора а в базисе { i, j, k }.
3. Собственные значения и собственные векторы матрицы.
Характеристическое уравнение
Во многих областях науки и техники, например, электро- и радиотехнике, механике, экономике, в теории кодирования и обработки сигналов широко используется понятие «собственное значение» и «собственный вектор».
Определение 25. Число l называется собственным значением, а ненулевой вектор х называется собственным вектором матрицы А, задающей линейное преобразование, если они связаны между собой соотношением
А х = lхÛ ( А-l Е ) х = О. ( 8 )
Это матричное уравнение задает систему однородных линейных уравнений:
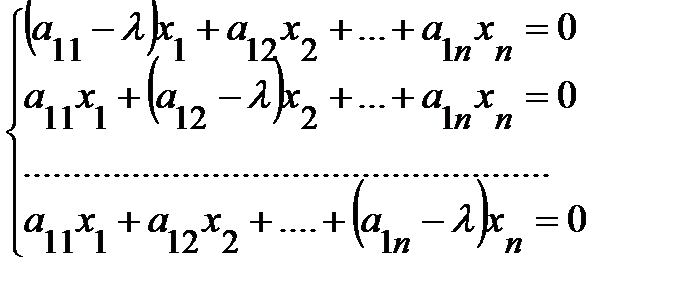, ( 9 )
которая имеет ненулевое решение в том случае, когда ее определитель |А-l Е| равен нулю.
Определение 26. Характеристическим уравнением квадратной матрицы А называется уравнение
|А-l Е| = 0 .
Пример 24. Найти собственные значения и собственные векторы линейного
преобразования с матрицей А =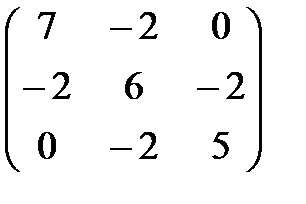 
.
Решение. Составим характеристическое уравнение |А-l Е| = 0 Þ
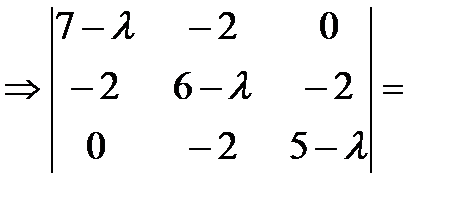(7 -l)[(5 -l)(6 -l) - 4] + 2 × (-2)(5 -l) =
= -l3 + 18l2- 99l + 162 = 0 Þ (l-3 )(l- 15l + 54) = (l- 3)(l- 6)(l- 9) = 0.
Таким образом нашли собственные значения линейного преобразования с матрицей А, равные: l1 = 3, l2 = 6, l3 = 9.
Найдем собственный вектор, соответствующий собственному значению
l1=3. Подставим l = 3 в систему ( 9 ) и получим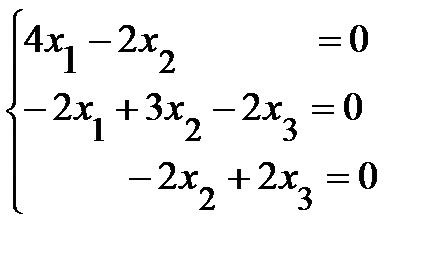 
.
С помощью элементарных преобразований получим систему, эквивалентную
данной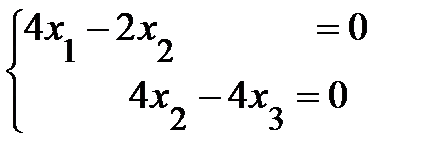 
, ранг которой r = 2. Так как число неизвестных в
системе n = 3 >r = 2, то в качестве базисных выберем переменные х1 и х2, а свободной переменной будет х3 . Полагая х3= 2t, где t – произвольное число, из последней системы найдем: х2 = 2t , х1 = t.
Таким образом собственному значению l1 = 3 соответствует собственный
вектор Х 1 =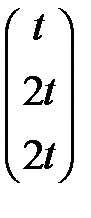 
. Аналогично, собственным значениям l2 = 6 и l3 = 9 соответствуют собственные векторы Х 2 = 
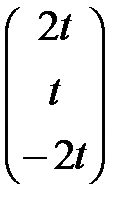и Х 3 = 
.
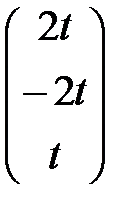Дата: 2018-11-18, просмотров: 521.
