При выполнении контрольных работ студент должен руководствоваться следующим.
1. Не следует приступать к выполнению контрольных работ до решения всех задач, рекомендованных в настоящем пособии.
2. Контрольные работы выполняются по УМД одного года издания. Замена издания другим в процессе изучения курса высшей математики не допускается.
3. Контрольная работа выполняется в обычной ученической тетради. Она должна быть аккуратно и четко написана. Для замечаний преподавателей на каждой странице оставляются поля шириной 3…4 см. Все страницы нумеруются. На обложку тетради наклеивают заполненный адресный бланк, а на первую страницу тетради - титульный бланк.
4. Решения задач в контрольных работах сопровождается исчерпывающими, но краткими объяснениями. Задачи располагаются в порядке номеров, указанных в заданиях; перед решением задачи выписывается полностью ее условие.
5. На рецензию одновременно высылается не более одной работы.
6. По получении из института прорецензированной работы студент обязан выполнить указания, сделанные рецензентом. В случае, если контрольная работа не зачтена, студент обязан в этой же тетради (после заключения рецензента) внести все исправления, решить заново задачи, указанные рецензентом, и представить работу на повторную рецензию.
7. Контрольная работа выполняется самостоятельно.
8. В конце работы указывается использованная литература.
9. Контрольная работа подписывается с указанием даты выполнения.
10. Контрольные работы, выполненные без соблюдения изложенных выше правил или по чужому варианту, не зачитываются и возвращаются.
Сдача экзаменов
К сдаче экзаменов допускаются студенты, имеющие на руках выполненные и зачтенные контрольные работы. Экзамены сдаются устно.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО РАЗДЕЛАМ КУРСА
ЛИНЕЙНАЯ АЛГЕБРА
1. Матрицы. Основные определения. Действия с матрицами
Определение 1. Прямоугольная таблица чисел или иных математических
выражений, состоящая из m строк и n столбцов
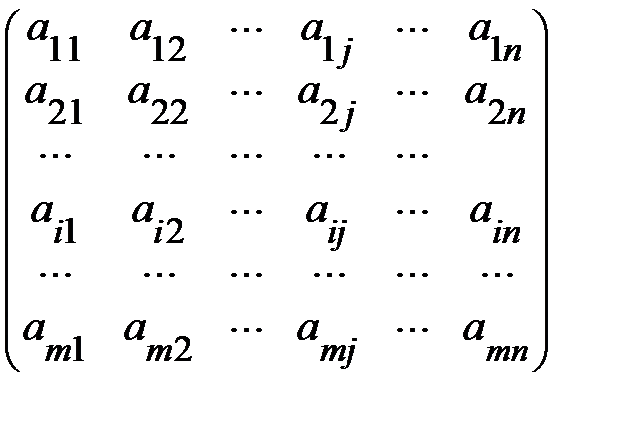-i - я строка 
- j - й столбец
называется матрицей.
Числа а ij , из которых составлена матрица, называются элементами матрицы.
Определение 2 . Матрица, состоящая из одной строки, называется
матрицей – строкой.
Определение 3. Матрица, состоящая из одного столбца, называется
матрицей – столбцом.
Определение 4. Матрица, у которой число строк совпадает с числом
столбцов, называется квадратной.
Пример 1.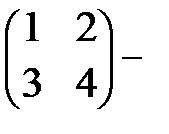 
квадратная матрица 2 – го порядка;
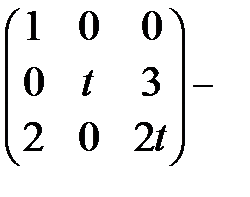квадратная матрица 3 – го порядка.
Обозначение: матрицы, как правило, обозначаются большими латинскими буквами А, В, С, …, или с указанием их размера m ´ n: А m ´ n , В m ´ n, … , а элементы матрицы обозначаются маленькими буквами а ij , в ij , с ij, … с индексами, указывающими на номер строки i и столбца j, в которых расположен указанный элемент.
Определение 5. Матрица, у которой все элементы с индексами i¹j (вне
главной диагонали) равны нулю, называется диагональной.
Пример 2.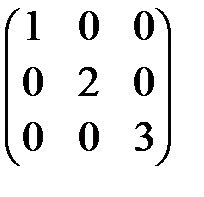 
; 
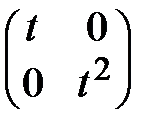- диагональные матрицы.
Определение 6. Единичной называется матрица Е с единицами на главной
диагонали:
Е =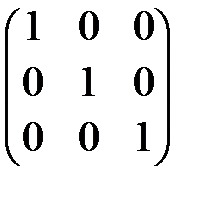 
.
Определение 7. Матрица, у которой все элементы равны нулю, называется
нулевой и обозначается О.
Определение 8. Матрицы А и В называются равными, если они имеют
одинаковые размеры и при этом элементы матриц А и В,
расположенные на одинаковых местах, равны между собой:
а i j = b i j "i , j .
Действие (или операция), согласно которому все строки некоторой произвольной матрицы А преобразуются в столбцы, а все столбцы этой матрицы преобразуются в строки, называется транспонированием. Транспонированная матрица обозначается А Т.
Определение 9. Матрица АТ, элементы которой а Т i j= а ij "i , j ,
называется транспонированной.
Пример 3. Если матрица А =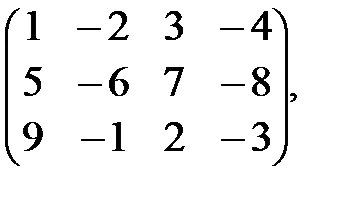 
то АТ =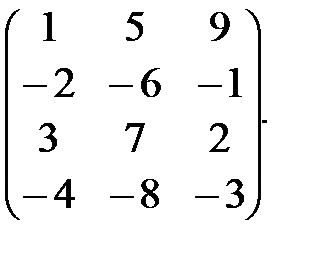 
Определение 10. Симметричной называется квадратная матрица, у
которой а ij = а ji"i , j (т.е. элементы, расположенные
симметрично относительно главной диагонали, равны).
Пример 4.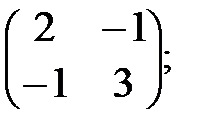 
.
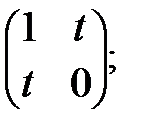
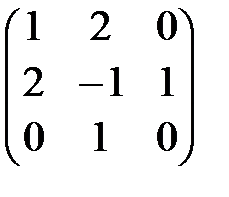Определение 11. Суммой матриц А и В одинаковых размеров называется
матрица С тех же размеров, элементы которой
с ij = а i j + в i j "i, j.
Пример 5.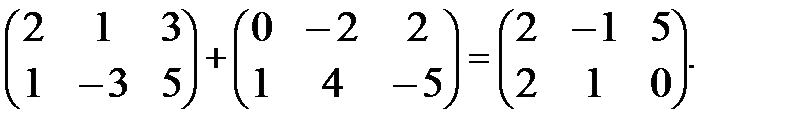 
Свойства сложения матриц
1. А + В = В + А (коммутативность).
2. (А + В) + С = А + ( В + С) (ассоциативность).
3. А + О = О + А = А .
Определение 12. Произведением матрицы на число l называется матрица В
тех же размеров, что и матрица А, причем b ij = l а ij "i , j .
Пример 6. 3×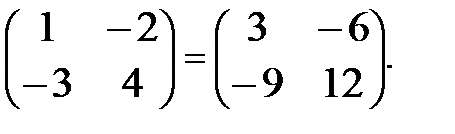 
Свойства умножения матрицы на число
1. l(mA) = (lm)A (ассоциативность).
2. l(A+ B) = lA + lB (дистрибутивность).
3. (l + m)A = lA + mA (дистрибутивность).
Пример 7. 2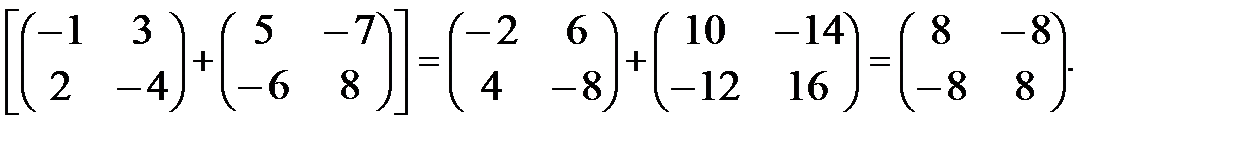 
Определение 13. Произведением двух матриц А и В называется матрица С,
у которой элемент с ij равен сумме произведений каждого
элемента i –й строки матрицы А на соответствующие
элементы j –го столбца матрицы В
c i j=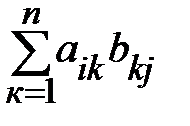 
(i = 1,2, …,m; j = 1,2, … , n).
Замечание 1. Умножение двух прямоугольных матриц возможно только в том случае, когда число столбцов левой матрицы равно числу строк правой матрицы, т.е.
А m ´ k × B k ´ n = C m ´ n .
Замечание 2. Произведением двух квадратных матриц А и В одинакового размера является квадратная матрица С того же размера.
Пример 8. Найти произведение АВ, если А =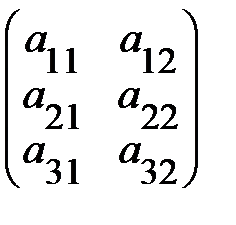 
и В = 
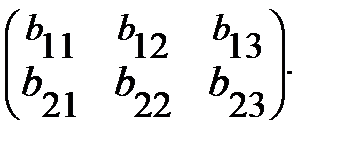
Решение. АВ =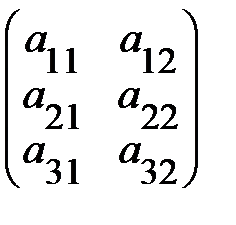
= 
.
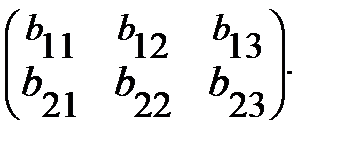
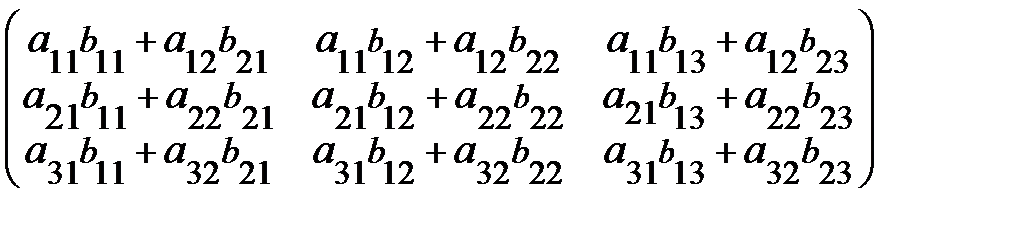Свойства умножения матриц
1. (АВ)С = А(ВС) (ассоциативность).
2. (А + В)С = АС + ВС (дистрибутивность).
3. АВ ¹ ВА (вообще говоря) – отсутвие коммутативности.
4. АО = О; ОА = О .
5. АЕ = А ;ЕА = А.
Определение 14. Матрицы А и В, для которых АВ = ВА называются
коммутирующими (или перестановочными).
Дата: 2018-11-18, просмотров: 456.
