ЛИНЕЙНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ

Ордена Трудового Красного Знамени федеральное государственное

бюджетное образовательное учреждение высшего образования

Московский технический университет связи и информатики

Кафедра теории вероятностей и прикладной математики

Учебно-методическое пособие

по курсу

ВЫСШАЯ МАТЕМАТИКА

Часть 1

ЛИНЕЙНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

для студентов-заочников 1 курса

(направления: 11.03.02, 15.03.04)

1 семестр

Москва 2017

План УМД на 2017/18 уч.г.

Учебно-методическое пособие

по курсу

ВЫСШАЯ МАТЕМАТИКА

Часть 1

ЛИНЕЙНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

Составители: А.В. Власов, доцент

В.С. Юдин, доцент

Издание утверждено на заседании кафедры. Протокол № 8 от 20.04.17 г.

Рецензент А.Г. Кюркчан, профессор

ВВЕДЕНИЕ

Студенты-заочники первого курса технических факультетов МТУСИ в течение первого семестра по курсу «Высшая математика» изучают две самостоятельные части:

«Линейная алгебра и аналитическая геометрия»;

«Высшая математика».

По этим курсам выполняются контрольные работы и сдается экзамен.

Настоящее учебно-методическое пособие и контрольная работа относятся к первой части курса.

Пособие не заменяет учебников по высшей математике. Оно содержит разъяснения о порядке изучения программного материала; в нем кратко освещены отдельные вопросы, которые могут встретить затруднение при самостоятельном изучении, приведены методы решения некоторых типовых задач и вопросы для самопроверки. Изучать курс следует по литературе, перечисленной в настоящем учебно-методическом пособии.

Бюджет времени (в часах) студента–заочника для изучения первой части курса «Высшая математика» в первом семестре:

Аудиторная работа		Самостоятельная работа		Итого
Лекции	Упражнения	Изучение курса	Выполнение контрольных работ
6	10	72	20	108

РАБОЧАЯ ПРОГРАММА

ОПРЕДЕЛИТЕЛИ

1. Определители и их основные свойства.

2. Системы линейных уравнений. Правило Крамера. Линейные однородные системы и их нетривиальные решения.

ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ

3. Понятие о линейном пространстве, размерности, линейных подпространствах, евклидовом (линейном со скалярным произведением) пространстве, норме, ортогональности.

4. Матрицы и действия над ними. Обратная матрица. Матричная запись системы линейных алгебраических уравнений и ее решения. Собственные значения и собственные векторы матриц; характеристическое уравнение.

ВЕКТОРЫ

5. Скалярные и векторные величины. Линейная комбинация векторов, базисы на плоскости и в пространстве, декартов базис.

6. Проекция вектора на ось. Разложение по ортогональному базису. Скалярное, векторное, смешанное произведение векторов, их основные свойства и выражения через декартовы координаты сомножителей. Физические приложения векторов и действия над ними.

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ

9. Линии и их уравнения. Порядок алгебраических линий. Примеры составления уравнения линий на плоскости по ее геометрическим свойствам.

10. Прямая линия. Различные виды уравнений прямой и их применение. Применение векторов к решению простейших задач на плоскости.

11. Кривые второго порядка. Определения, канонические уравнения, основные характеристики.

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ

12. Поверхности, линии и их уравнения. Порядок алгебраической поверхности. Поверхности вращения.

13. Плоскость и прямая линия. Различные виды их уравнений. Применение векторной алгебры для решения основных задач.

14. Поверхности второго порядка. Канонические уравнения поверхностей и исследование их форм методом сечений. Понятия о плоскостях сечения круговых цилиндра и конуса.

СПИСОК ЛИТЕРАТУРЫ

1. Пискунов Н.С. Дифференциальное и интегральное исчисление. Т. 2. Изд. 13-е. - М.: Наука, 1985.

2. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. Изд. 6-е. - М.: Наука, 1987.

3. Привалов И.И. Аналитическая геометрия. – СПб.: Лань, 2005.

4. Ефимов Н.В. Краткий курс аналитической геометрии. – М.: Физматлиз, 2004.

5. Данко П.Е., Попов А.Г., Кожевникова Т.Я., Данко С.П. Высшая математика в задачах и упражнениях. Ч. 1. - М.: «Оникс, Мир образования», 2007.

6. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. - М.: Дрофа, 2005.

ТЕМАТИКА ЛЕКЦИЙ

1. Элементы линейной алгебры. Определители. Числовые матрицы и действия над ними. Обратная матрица (2 ч.).

2. Системы линейных уравнений. Элементы векторной алгебры (1 ч.).

3. Аналитическая геометрия на плоскости. Прямая на плоскости. Основные кривые 2-го порядка (краткий обзор) (1 ч.).

4. Аналитическая геометрия в пространстве. Плоскость и прямая в пространстве. Основные поверхности 2-го порядка (краткий обзор) (2 ч.).

ТЕМАТИКА УПРАЖНЕНИЙ

1. Матрицы и действия сними. Определители и их вычисление. Обратная матрица. Ранг матрицы.

2. Системы линейных уравнений. Решение систем уравнений матричным методом, по формулам Крамера, методом Гаусса. Исследование систем уравнений на совместность. Линейные преобразования.

3. Действия с векторами. Собственные числа и собственные векторы. Скалярное, векторное и смешанное произведения векторов.

4. Уравнения прямой на плоскости. Кривые 2-го порядка.

5. Плоскость и прямая в пространстве.

ОБЩИЕ УКАЗАНИЯ

Самостоятельная работа над учебником

Самостоятельная работа над учебником является основным видом работы студента-заочника.

В самостоятельной работе следует руководствоваться следующими положениями.

1. Изучать курс высшей математики следует систематически в течение всего учебного процесса. Изучение в сжатые сроки перед экзаменом не дает глубоких и прочных знаний.

2. Все выкладки и вычисления необходимо проделывать на бумаге. Чтение учебного пособия следует сопровождать изучением конспекта, в котором записываются определения основных понятий курса, формулы, теоремы, а также воспроизводятся соответствующие чертежи и графики. На полях конспекта следует отмечать вопросы, выделенные студентом для консультации с преподавателем.

3. Работая по основному учебнику, рекомендованному в настоящем пособии, студент должен обращаться к указанной дополнительной литературе. Это необходимо в тех случаях, когда основной учебник не дает полного ответа на некоторые вопросы программы. Кроме того, в дополнительной литературе, разработанной в основном преподавателями МТУСИ, учтен профиль университета, приведено много примеров и задач, облегчающих последующее изучение специальных дисциплин.

Решение задач

Приступая к решению задач, следует после изучения очередного раздела по учебнику внимательно рассмотреть примеры решения типовых задач по данному пособию, а затем переходить к самостоятельному решению рекомендованных задач. В тех случаях, когда это возможно, следует дать чертеж, поясняющий содержание задачи. Решение следует сопровождать краткими, но исчерпывающими пояснениями. Решение каждой задачи должно доводиться до окончательного ответа и по возможности приводиться в общем виде.

Числовые данные подставляются в формулу в конце решения задачи. В промежуточные вычисления не следует вводить приближенные значения корней, число p и т.д.

3. Выбор варианта

Вариант выбирается в соответствии с двумя последними цифрами студенческого билета. Например, если номер студенческого билета 810221, то вариант будет иметь номер 21.

Сдача экзаменов

К сдаче экзаменов допускаются студенты, имеющие на руках выполненные и зачтенные контрольные работы. Экзамены сдаются устно.

ЛИНЕЙНАЯ АЛГЕБРА

1. Матрицы. Основные определения. Действия с матрицами

Определение 1. Прямоугольная таблица чисел или иных математических

выражений, состоящая из m строк и n столбцов

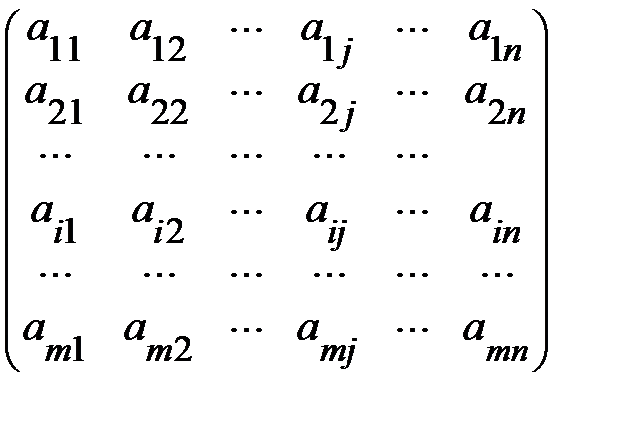-i - я строка

- j - й столбец

называется матрицей.

Числа а _ij , из которых составлена матрица, называются элементами матрицы.

Определение 2 . Матрица, состоящая из одной строки, называется

матрицей – строкой.

Определение 3. Матрица, состоящая из одного столбца, называется

матрицей – столбцом.

Определение 4. Матрица, у которой число строк совпадает с числом

столбцов, называется квадратной.

Пример 1. 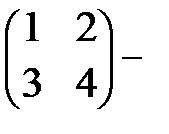квадратная матрица 2 – го порядка;

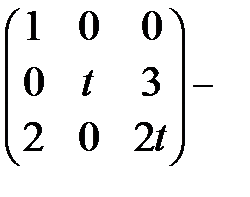квадратная матрица 3 – го порядка.

Обозначение: матрицы, как правило, обозначаются большими латинскими буквами А, В, С, …, или с указанием их размера m ´ n: А _m _´ _n , В _m _´ _n, … , а элементы матрицы обозначаются маленькими буквами а _ij , в _ij , с _ij, … с индексами, указывающими на номер строки i и столбца j, в которых расположен указанный элемент.

Определение 5. Матрица, у которой все элементы с индексами i¹j (вне

главной диагонали) равны нулю, называется диагональной.

Пример 2. 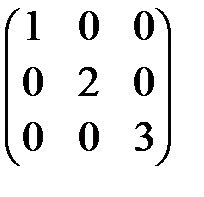; 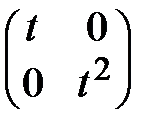- диагональные матрицы.

Определение 6. Единичной называется матрица Е с единицами на главной

диагонали:

Е = .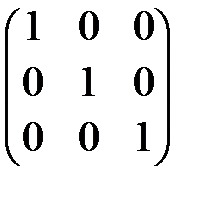

Определение 7. Матрица, у которой все элементы равны нулю, называется

нулевой и обозначается О.

Определение 8. Матрицы А и В называются равными, если они имеют

одинаковые размеры и при этом элементы матриц А и В,

расположенные на одинаковых местах, равны между собой:

а _i _j = b _i _j "i , j .

Действие (или операция), согласно которому все строки некоторой произвольной матрицы А преобразуются в столбцы, а все столбцы этой матрицы преобразуются в строки, называется транспонированием. Транспонированная матрица обозначается А ^Т.

Определение 9. Матрица А^Т, элементы которой а ^Т _i _j= а _ij "i , j ,

называется транспонированной.

Пример 3. Если матрица А = 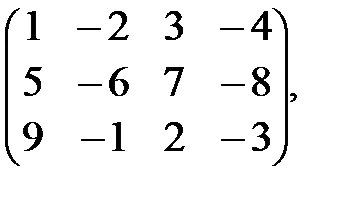то А^Т =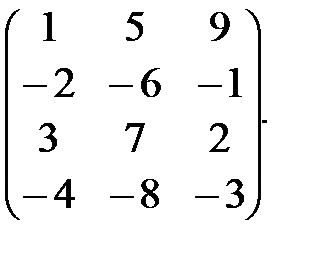

Определение 10. Симметричной называется квадратная матрица, у

которой а _ij = а _ji"i , j (т.е. элементы, расположенные

симметрично относительно главной диагонали, равны).

Пример 4. .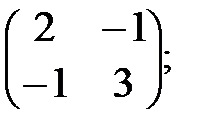

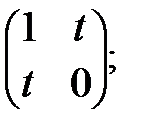
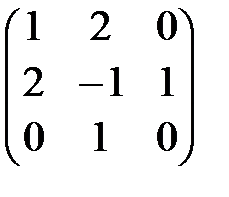Определение 11. Суммой матриц А и В одинаковых размеров называется

матрица С тех же размеров, элементы которой

с _{ij =} а _{i j} + в _{i j}"i, j.

Пример 5.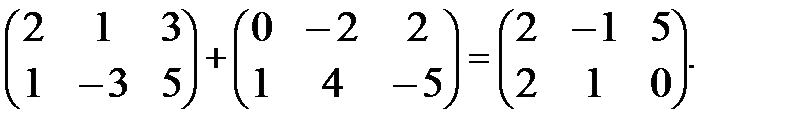

Свойства сложения матриц

1. А + В = В + А (коммутативность).

2. (А + В) + С = А + ( В + С) (ассоциативность).

3. А + О = О + А = А .

Определение 12. Произведением матрицы на число l называется матрица В

тех же размеров, что и матрица А, причем b _ij = l а _ij "i , j .

Пример 6. 3×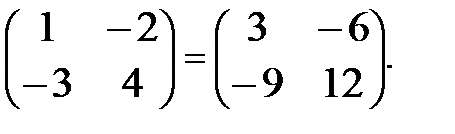

Свойства умножения матрицы на число

1. l(mA) = (lm)A (ассоциативность).

2. l(A+ B) = lA + lB (дистрибутивность).

3. (l + m)A = lA + mA (дистрибутивность).

Пример 7. 2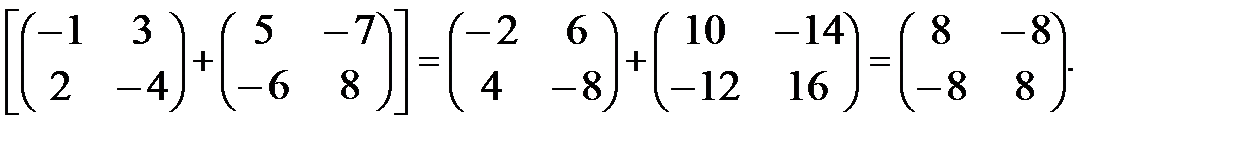

Определение 13. Произведением двух матриц А и В называется матрица С,

у которой элемент с _ij равен сумме произведений каждого

элемента i –й строки матрицы А на соответствующие

элементы j –го столбца матрицы В

c _i _j= 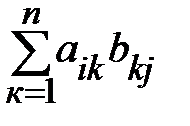(i = 1,2, …,m; j = 1,2, … , n).

Замечание 1. Умножение двух прямоугольных матриц возможно только в том случае, когда число столбцов левой матрицы равно числу строк правой матрицы, т.е.

А _m _´ _k × B _k _´ _n = C _m _´ _n .

Замечание 2. Произведением двух квадратных матриц А и В одинакового размера является квадратная матрица С того же размера.

Пример 8. Найти произведение АВ, если А = 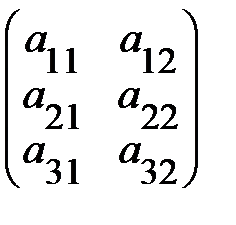и В =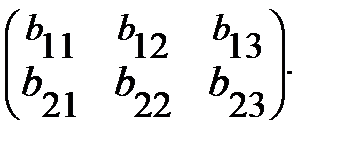

Решение. АВ =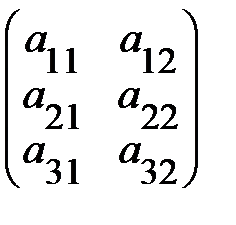

= .

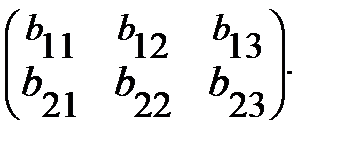
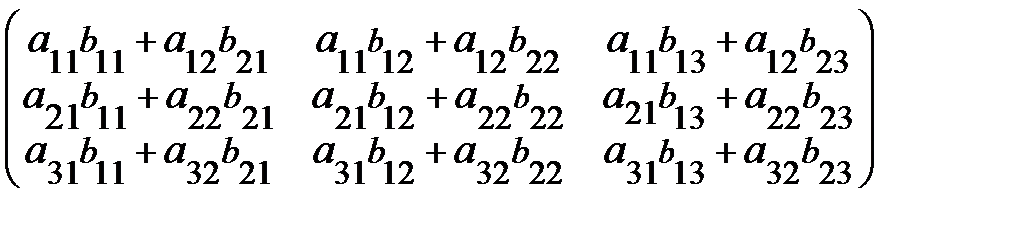Свойства умножения матриц

1. (АВ)С = А(ВС) (ассоциативность).

2. (А + В)С = АС + ВС (дистрибутивность).

3. АВ ¹ ВА (вообще говоря) – отсутвие коммутативности.

4. АО = О; ОА = О .

5. АЕ = А ;ЕА = А.

Определение 14. Матрицы А и В, для которых АВ = ВА называются

коммутирующими (или перестановочными).

Вопросы для самопроверки

1. Какие матрицы называются равными, диагональными, транспонированными, симметрическими, перестановочными?

2. Сформулируйте свойства сложения матриц.

3. Сформулируйти правило умножения двух матриц. В чем состоит условиие, необходимое для существования произведения матриц?

4. Сформулируйте свойства умножения матриц.

5. Как определяется обратная матрица? В чем состоит условие, необходимое для существования обратной матрицы?

6. Какие существуют правила для вычисления определителей 3-го порядка?

7. Что называется минором некоторого элемента определителя 3-го (произвольного) порядка?

8. Что называется алгебраическим дополнением некоторого элемента определителя третьего (произвольного) порядка?

9. Напишите разложение определителя 3-го порядка по 3-й строке и по 3-му столбцу.

10. Сформулируйте свойства определителей.

11. Что называется рангом матрицы и как он вычисляется?

ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ

Векторы и действия над ними

Следует различать два типа объектов, встречающихся в естествознании: скалярные и векторные величины.

Скалярные величины – это величины, которые характеризуются числовым значением. Например, скалярными величинами являются масса тела, давление, коэффициент трения и т.д.

Векторные величины – это величины, которые кроме числового значения характеризуются еще направлением. Примерами таких величин являются: скорость тела, сила, действующая на тело, импульс тела и т.д.

Вектором называется направленный отрезок 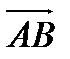с начальной точкой А и конечной точкой В, который можно перемещать параллельно самому себе.

Длиной 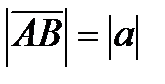вектора 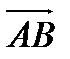= а называется число (неотрицательное), равное длине отрезка АВ, соединяющего точки А и В.

Нулевой вектор – вектор, начальная и конечная точки которого совпадают: 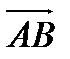= = 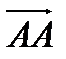О . Его длина равна нулю ( |О| = 0 ), а направление для него не имеет смысла.

Единичный вектор е - вектор, длина которого равна 1 ( |е| = 1).

Коллинеарные векторы – векторы, лежащие на одной прямой или на параллельных прямых. Векторы а , b и c , изображенные на рис. 1, коллинеарны.

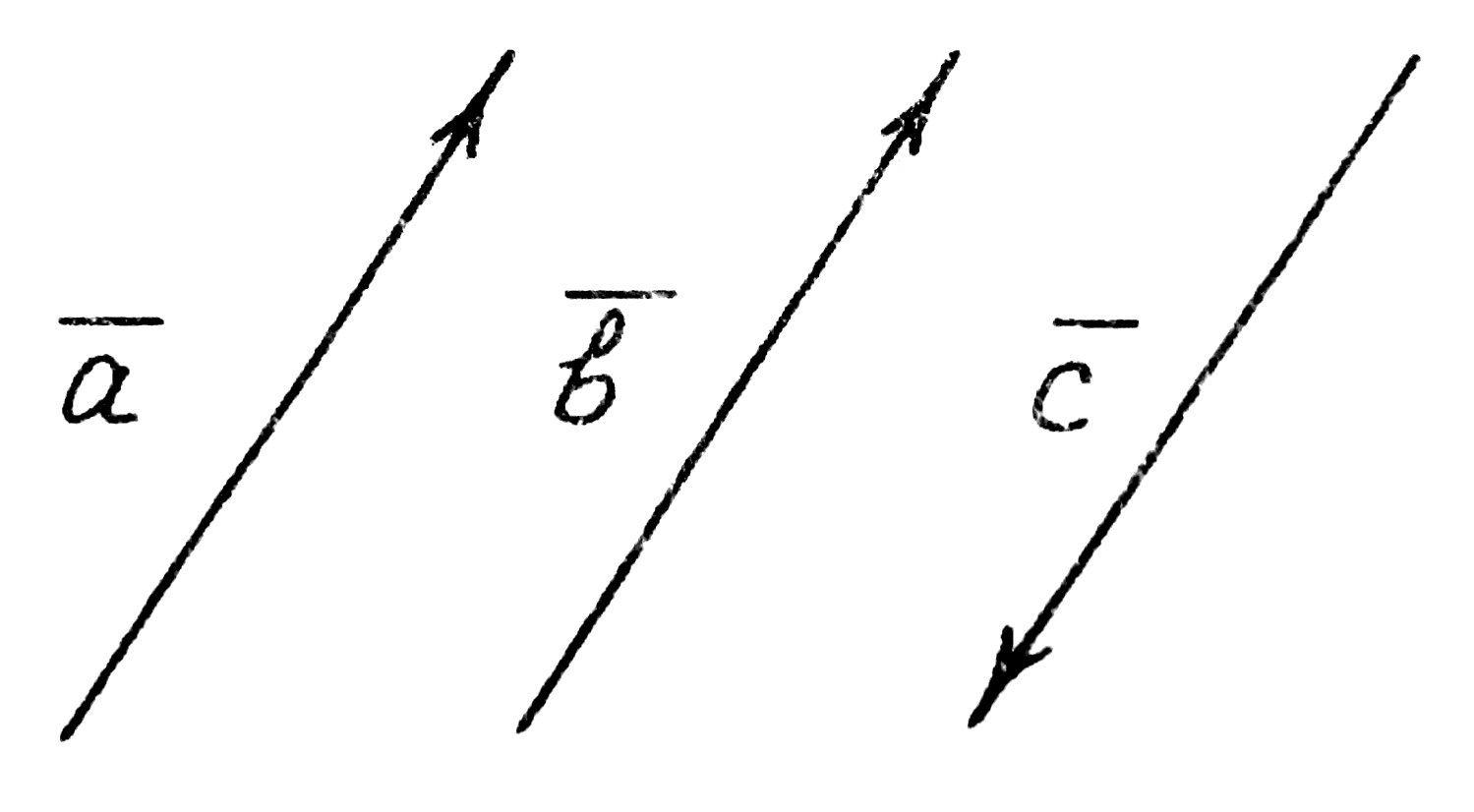
Рис. 1

Компланарные векторы – векторы, которые лежат в одной плоскости или в параллельных плоскостях.

Равные векторы – векторы, которые коллинеарны, имеют одинаковую длину и одинаковое направление.

Суммой а + b векторов а и b называется вектор, идущий из начала вектора а в конец вектора b, если начало вектора b совпадает с концом вектора а (т.е. вектор b приложен к вектору а) – это правило треугольника (рис. 2).

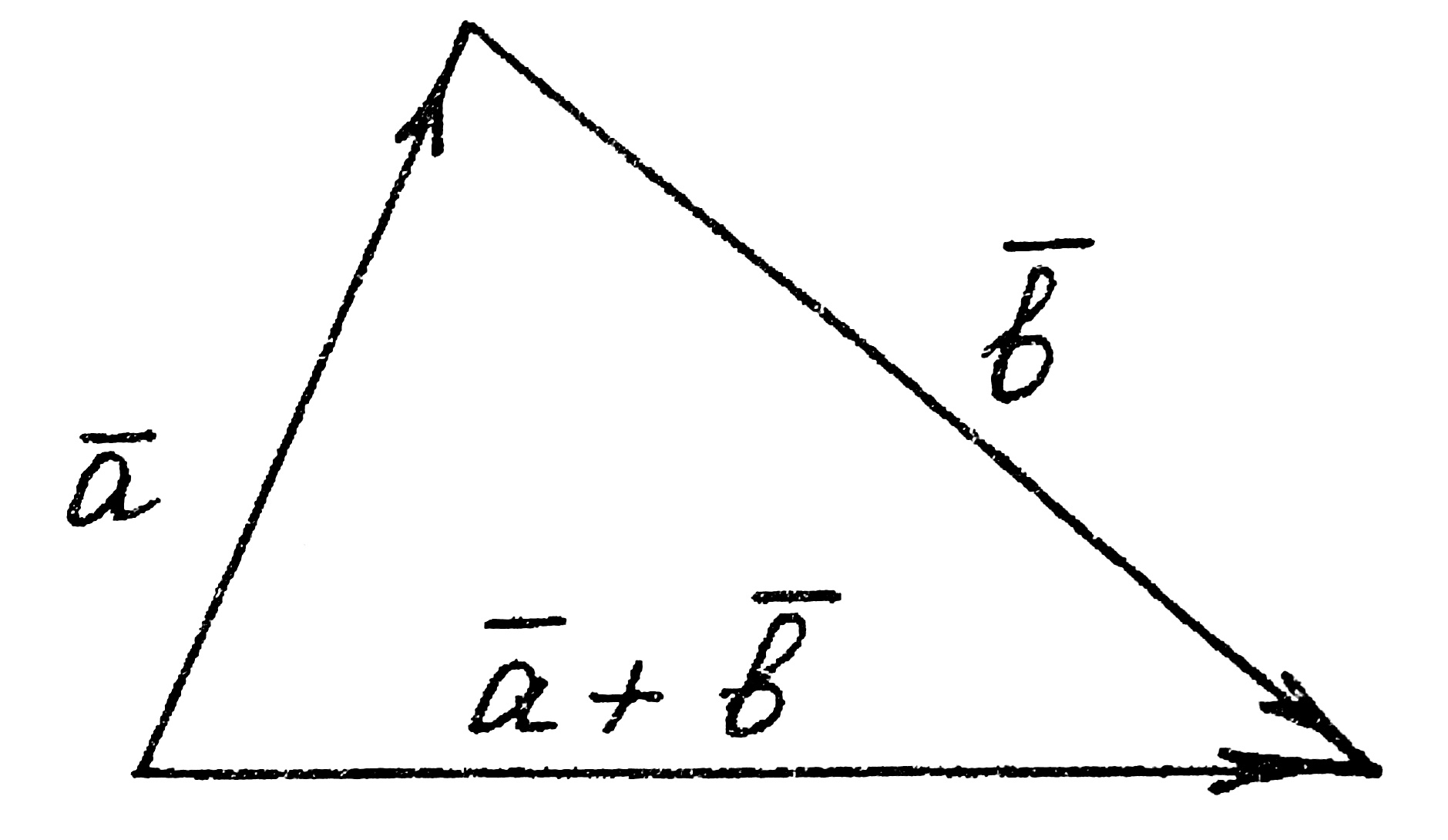
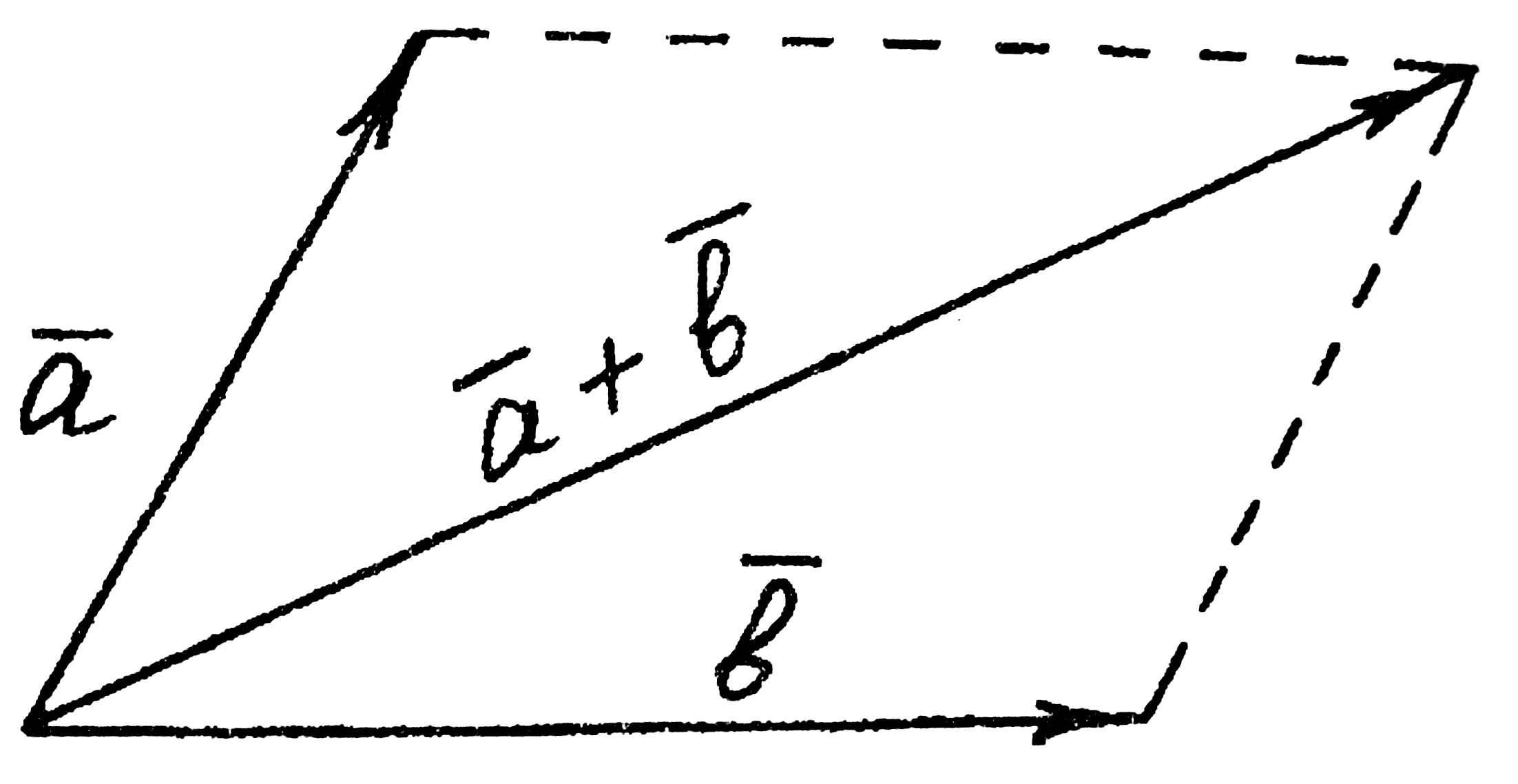
Рис. 2 Рис. 3

Если векторы а и b имеют общее начало и на них как на сторонах построен параллелограмм, то суммой а + b будет диагональ параллелограмма.

Правило вычитания векторов показано на рис. 3 .

Произведением lа (или аl) вектора а на действительное число l называется вектор b, коллинеарный вектору а, длина которого |lа½= |l|×|а|, а направление совпадает с вектором а , если l > 0 , или противоположно а, если l < 0.

Проекцией точки А на прямую l называется точка А^*, в которой пересекается прямая l с плоскостью, перпендикулярной к l, проходящей через точку А (рис. 4).

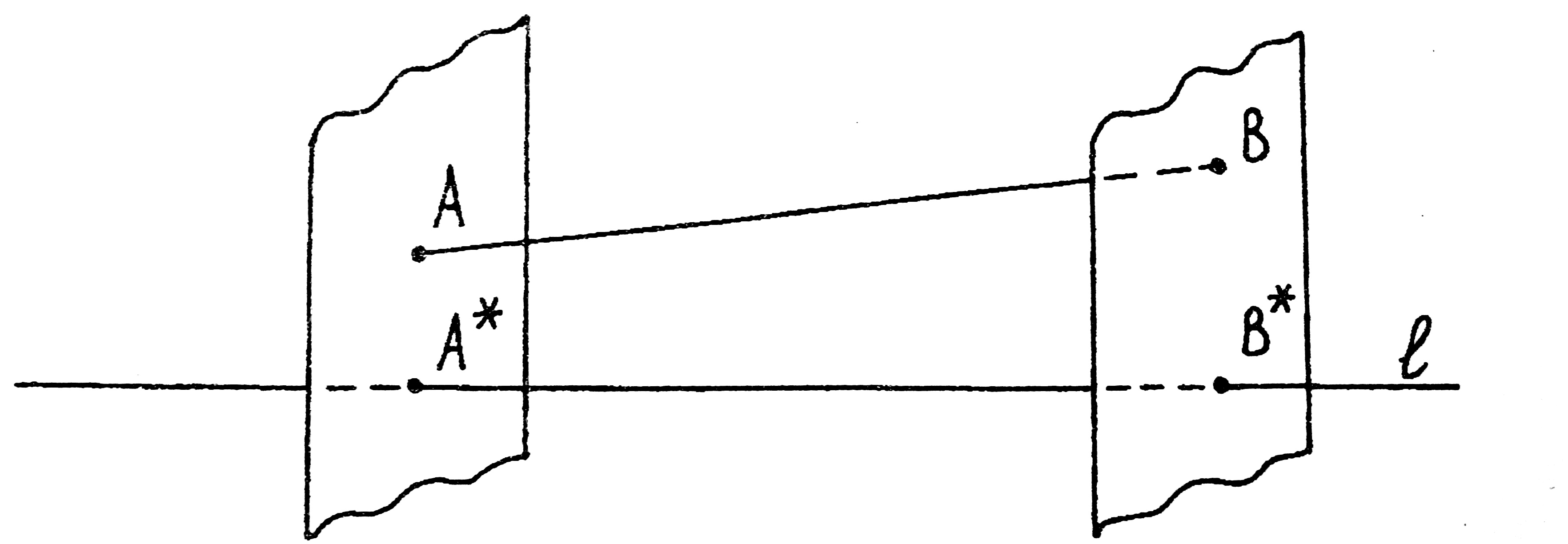
Рис. 4

Проекцией вектора а = 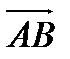(рис. 4) на направленную прямую l называется вектор 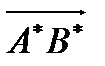, где А^*и В^* соответственно проекции точек А, В на прямую l.

Проекция вектора а = 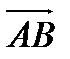на направленную прямую l будем обозначать символом 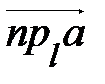(пр_lа ) .

Числовой проекцией |пр_lа| вектора а на направленную прямую l называется произведение длины вектора а на косинус угла a между вектором а и прямой l

|пр_lа| = |а|×cos ( а,l ) = |а|×cosa ( 0 £a£p ).

2. Линейное пространство. Линейная зависимость. Базис

Линейным пространством L называется множество элементов, для которых определены операции сложения двух векторов и умножения вектора на число, обладающие следующими свойствами

1. Для любых векторов а и b из линейного пространства

а + b = b + а (коммутативность сложения).

В символьной записи это свойство будет иметь вид

" a, b Î L Þ а + b = b + а .

2. " a, b ,с Î L Þ( а + b) + с = а + ( b + c) ( ассоциативность).

3. $ О Î L : " a Î L Þ а + О = а (существование нулевого вектора).

4. " a Î L $ (- а) Î L (противоположный вектор) : а + (-а) = О.

5. " l Î R, " a, b Î L Þ l (а + b ) = lа +lb.

6. " l₁, l₂Î R , " a Î L Þ ( l₁ + l₂) а = l₁а + l₂а .

7. " l₁, l₂Î R , " a Î L Þ ( l₁×l₂) а = l₁(l₂а ).

8. " a Î L Þ 1×а = а .

Линейными пространствами, в частности, являются: множество действительных чисел; множество векторов на плоскости или в пространстве; множество всех функций, определенных на каком-нибудь отрезке и т.д.

Определение 21. Линейной комбинацией векторов а₁, а₂, …, а_n называется

сумма с₁ а₁ + с₂а₂ + …+ с_nа_n, где коэффициенты

с₁, с₂, …, с_n– действительные числа.

Определение 22. Совокупность векторов а₁, а₂, …, а_n линейного

пространства называется линейной зависимой, если их

линейная комбинация равна нулю

с₁ а₁ + с₂а₂ + …+ с_n а_n = 0

и при этом хотя бы один из коэффициентов с₁, с₂, …, с_n

отличен от нуля.

Определение 23. Совокупность векторов а₁, а₂, …, а_n называется

линейно независимой, если равенство

с₁ а₁ + с₂а₂ + …+ с_nа_n= 0

выполняется лишь в случае, когда все коэффициенты

с₁, с₂, …, с_n равны нулю.

Утверждение 1. Необходимым и достаточным условием линейной зависимости двух векторов на плоскости является их коллинеарность.

Утверждение 2. Необходимым и достаточным условием линейной зависимости трех векторов в пространстве является их компланарность.

Определение 24. Базисом в линейном пространстве L называется

упорядоченная система А ( А = { а₁, а₂, …, а_n })

максимально возможного числа векторов {а₁, а₂, …, а_n},

удовлетворяющая условиям:

1) совокупность векторов а₁, а₂, …, а_n линейно независима;

2) любой вектор a Î L в системе векторов А единственным

образом представляется в виде их линейной комбинации

а = х₁ а₁ + х₂а₂ + …+ х_n а_n.

Числа ( х₁, х₂, …, х_n ) называются координатами вектора а в базисе

{ а₁, а₂, …, а_n }.

Размерность линейного пространства L определяется максимальным числом n линейно независимых векторов и обозначается dim L (dim L = n ). Если это число конечно, то такое пространство L называется конечномерным.

Любая пара неколлинеарных векторов а₁, а₂ на плоскости является базисом множества всех векторов, лежащих на плоскости.

Любая тройка некомпланарных векторов а₁, а₂, а₃ в трехмерном пространстве является базисом множества всех векторов, лежащих в этом пространстве.

В случае декартовой прямоугольной

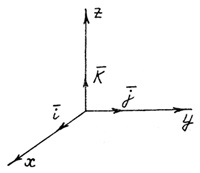системы координат в трехмерном

пространстве в качестве базисных выбирают

единичные векторы

i = (1,0,0), j = (0,1,0), k = (0,0,1) ,

которые:

а) линейно независимы;

б) имеют длину, равную единице, т.е. |i| = |j| = |k| = 1;

c) по направлению совпадают с направлением осей

Рис. 5 координат OX , OY , OZ.

Векторы i, j ,k называются ортами и образуют базис.

Любой произвольный вектор а в этом трехмерном базисе может быть представлен в виде линейной комбинации а = х i + у j + z k или а = ( х, у, z ), где х, у, z - координаты ветора а в базисе { i, j, k }.

3. Собственные значения и собственные векторы матрицы.

Характеристическое уравнение

Во многих областях науки и техники, например, электро- и радиотехнике, механике, экономике, в теории кодирования и обработки сигналов широко используется понятие «собственное значение» и «собственный вектор».

Определение 25. Число l называется собственным значением, а ненулевой вектор х называется собственным вектором матрицы А, задающей линейное преобразование, если они связаны между собой соотношением

А х = lхÛ ( А-l Е ) х = О. ( 8 )

Это матричное уравнение задает систему однородных линейных уравнений:

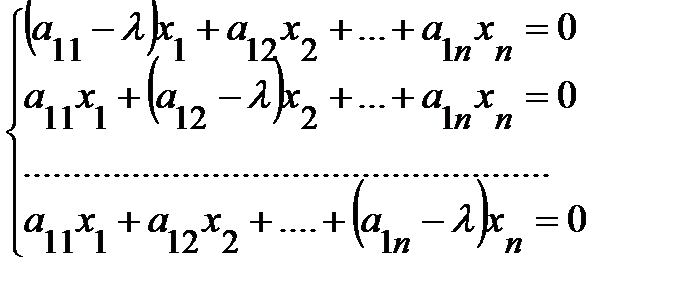, ( 9 )

которая имеет ненулевое решение в том случае, когда ее определитель |А-l Е| равен нулю.

Определение 26. Характеристическим уравнением квадратной матрицы А называется уравнение

|А-l Е| = 0 .

Пример 24. Найти собственные значения и собственные векторы линейного

преобразования с матрицей А = .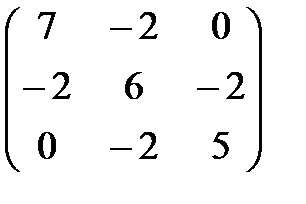

Решение. Составим характеристическое уравнение |А-l Е| = 0 Þ

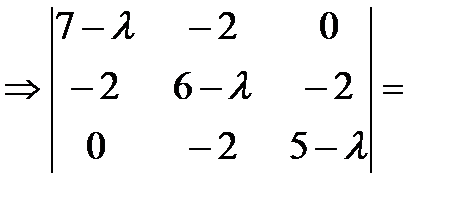(7 -l)[(5 -l)(6 -l) - 4] + 2 × (-2)(5 -l) =

= -l³ + 18l²- 99l + 162 = 0 Þ (l-3 )(l- 15l + 54) = (l- 3)(l- 6)(l- 9) = 0.

Таким образом нашли собственные значения линейного преобразования с матрицей А, равные: l₁ = 3, l₂ = 6, l₃ = 9.

Найдем собственный вектор, соответствующий собственному значению

l₁=3. Подставим l = 3 в систему ( 9 ) и получим .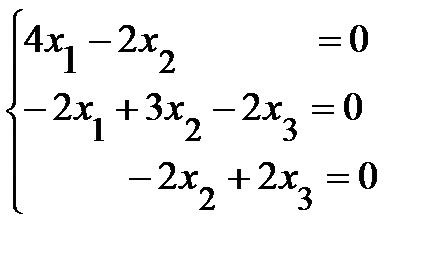

С помощью элементарных преобразований получим систему, эквивалентную

данной 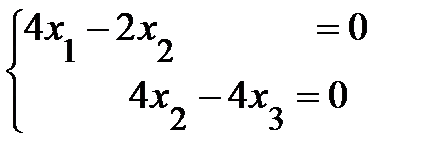, ранг которой r = 2. Так как число неизвестных в

системе n = 3 >r = 2, то в качестве базисных выберем переменные х₁ и х₂, а свободной переменной будет х₃ . Полагая х₃= 2t, где t – произвольное число, из последней системы найдем: х₂ = 2t , х₁ = t.

Таким образом собственному значению l₁ = 3 соответствует собственный

вектор Х ₁ = 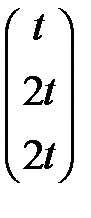. Аналогично, собственным значениям l₂ = 6 и l₃ = 9 соответствуют собственные векторы Х ₂ = 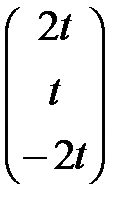и Х ₃ = .

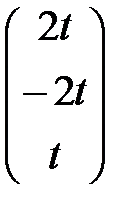АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

Вопросы для самопроверки

1. Что такое эллипс и каково его каноническое уравнение?

2. Что такое гипербола и каково ее каноническое уравнение?

3. Что такое парабола и каково ее каноническое уравнение?

4. Что такое эксцентриситет и каким он может быть у эллипса, у

гиперболы, у параболы?

5. Какие из кривых второго порядка имеют асимптоты и каковы их

уравнения?

6. Какая линия называется алгебраической и как определяется ее порядок?

2. Аналитическая геометрия в пространстве

Плоскость и прямая линия

Вопросы для самопроверки

1. Объясните смысл параметров в уравнениях

; .

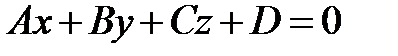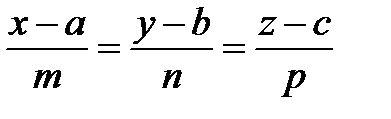2. Напишите уравнения:

а) плоскости ХОZ;

б) осей ОУ, ОХ, ОZ.

3. Каково взаимное расположение прямой

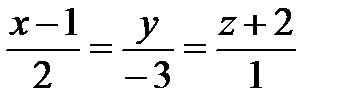
и плоскости 3х + 2у – 5 = 0?

2.3 Поверхности 2-го порядка

Студент должен уметь распознавать указанные в таблице две поверхности 2-го порядка по их каноническим уравнениям, используя при этом метод сечений.

Таблица 2

Каноническое уравнение	Название	Схематический чертеж
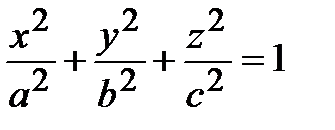
	Трехосный эллипсоид
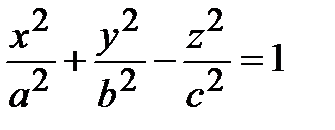
	Однополостный гиперболоид
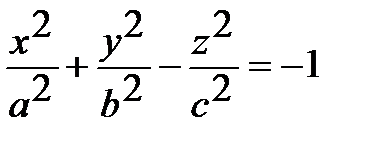
	Двуполостный гиперболоид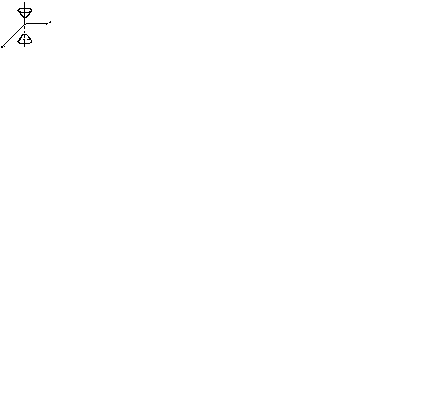
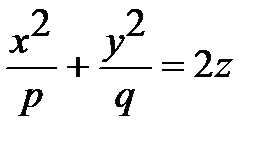
	Эллиптический параболоид
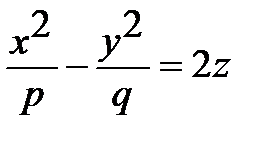
	Гиперболический параболоид
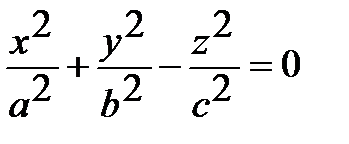
	Конус 2-го порядка

Следует, также, обратить внимание на цилиндры 2-го порядка

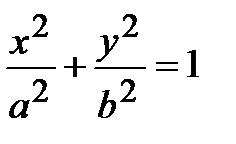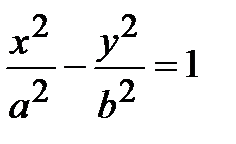; ; у²= 2рх

и на поверхности вращения 2-го порядка. Например, если в уравнении однополостного гиперболоида

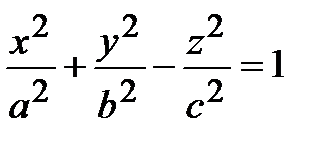
Положить а = b, то в сечении поверхности плоскостью z = h будут получаться окружности

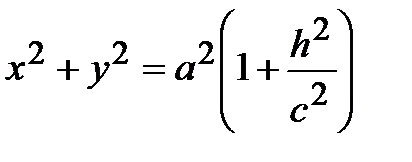следовательно, в этом случае поверхность является однополостным гиперболоидом вращения (он получается вращением гиперболы

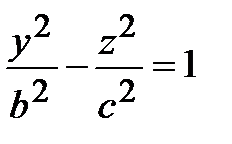вокруг оси ОZ).

Пример 32. Составить уравнение поверхности, образованной вращением линии x² - pz² = 4 вокруг оси OZ. Подобрать значение параметра р так, чтобы точка А(1,2,-1) лежала на этой поверхности. Указать название полученной поверхности и сделать её эскиз.

Решение. Уравнением вращения линии F(x,z) = 0 вокруг оси OZ является уравнение

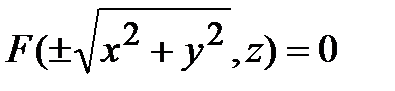так как при вращении вокруг оси OZ в уравнении без изменения остается координата z , а х заменяется на 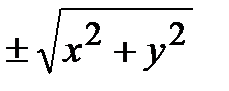(аналогичный факт имеет место и по отношению к поверхностям, получаемым вращением плоских линий вокруг других координатных осей).

Таким образом, в рассматриваемом примере получим уравнение

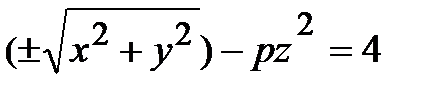или x² + y² – pz² = 4.

Найдем параметр р , учитывая требования задачи. Координаты точки А должны удовлетворять найденному уравнению поверхности. Подставляя координаты точки в уравнение, получим 1+ 4 - р = 4 Þр = 1. Тогда искомое уравнение примет вид

x²+ y²– z² = 4 или в канонической форме .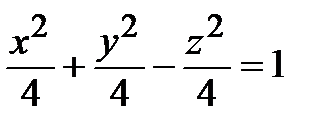

Это уравнение описывает однополостный гиперболоид вращения.

Пример 33. Построить поверхность, определяемую уравнением:

9 x² + 4 y²+ 36 z² -18x - 16y +216 z + 313 = 0.

Для выполнения задания необходимо:

а) привести данное уравнение поверхности к каноническому виду;

б) определить вид поверхности и ее расположение относительно системы координат;

с) записать название поверхности и сделать чертеж.

Решение. Группируем члены уравнения, содержащие одинаковые переменные:

(9 x²- 18 x) + (4 y²- 16 y) + (36 z²+ 216 z) + 313=0 Þ

9( x²- 2 x) + 4( y²- 4 y) + 36( z²+ 6 z) + 313=0.

Выделяем полный квадрат в каждой скобке:

9((x²- 2x +1) - 1) + 4((y²- 4y+ 4) - 4)+36((z²+ 6z + 9) - 9) + 313 = 0 .

Получим 9((x-1) ²-1) + 4((y-2) ²- 4) + 36((z+3) ²-9) + 313 = 0 Þ

9(x-1) ²-9 + 4(y-1) ²-16 + 36(z+3) ²-324 + 313=0 Þ

9(x-1) ²+ 4(y-2) ²+ 36(z+ 3) ² = 36 .

Разделим обе части уравнения на свободный член и получим каноническое уравнение эллипсоида с центром в точке О₁(1,2,-3)

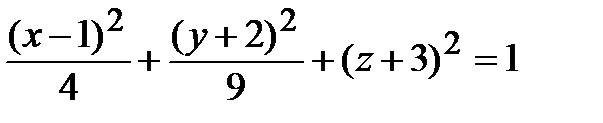Для построения этого эллипсоида сделаем в уравнении замену переменных

x-1= x₁, y-2 = y₁, z +3 = z₁ .

В новых переменных уравнение эллипсоида примет вид:

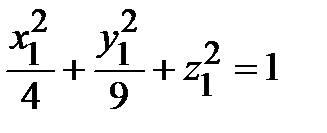Сделаем чертеж. Для этого через центр эллипсоида O₁(1,2,-3) проведем оси

O₁X₁, O₁Y_1,O₁Z₁ , и в этой системе координат построим эллипсоид

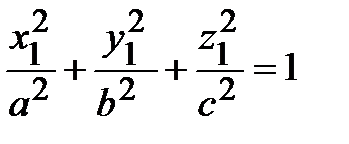, где a = 2 , b = 3 , c = 1 (рис. 7).

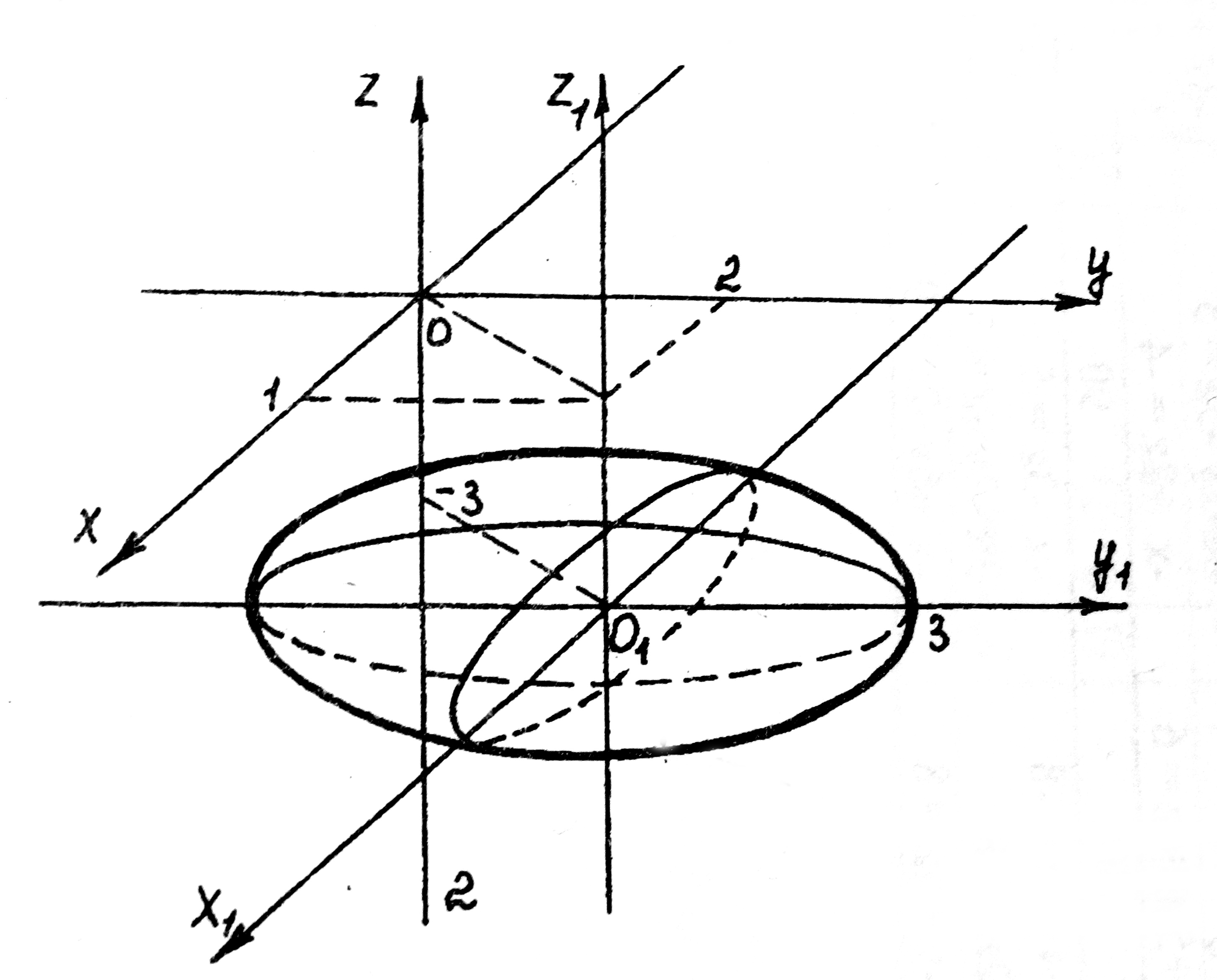
Рис. 7

Вопросы для самопроверки

1. Какие поверхности заданы уравнениями:

4x²+9y²+z²= 36 ;

4x²+9y²-z²= 36 ;

4x²+9y²-z²= -36 ;

3x²+4y²= z² ;

3x²- 4y²= z²;

x²+ y²= z ;

x²+ z²= 1;

x²– z²= 0 ;

y²= 4x .

2. Составить уравнение поверхности, образованной вращением прямой

у = kх вокруг оси ОХ.

3. Какую поверхность в пространстве описывает алгебрарическое уравнение 2-го порядка, содержащее лишь две переменные?

Контрольная работа № 1

Вариант 0

1. Решить систему линейных уравнений матричным методом и по формулам Крамера.

Варианты		Варианты
10	-5x +4y -3z = 6 -6x - 2y +5z = 9 4x - y - 3z = -8	60	-3x + 4y +5z = -4 -5x +5y +5z = -5 2y - z = 3
20	-2y +3z = -8 3x +y +3z = 1 -x +y +z = -3	70	3x - 4y - 4z = - 6 5x + 3y + z = - 8 4x + 2y - 3z = -3
30	-y - 5z = 2 -5x +y +2z = - 4 -5x +5y +4z = 6	80	3x +4y -z = -8 y - 2z = -8 -3x -y +3z = 8
40	-4x -6y -z = -1 -x -2y -5z = 5 -x +2z = -4	90	-x -3z = 5 3x -2y -z = 3 -x +6y -2z = 9
50	x +4y +z = 7 -3x +2y +z = -1 5x -2y -2z = 5	00	-x -3y = 5 -3x +y +z = -2 -2x +y +3z = 5

2. Даны координаты вершин треугольника АВС. Требуется:

1) вычислить длину стороны ВС;

2) составить уравнение стороны ВС;

3) вычислить длину высоты, проведенной из вершины А;

4) составить уравнение этой высоты.

Варианты	10	20	30	40	50
А(x₁;y₁;) В(x₂;y₂;) С(x₃;y₃;)	(-5, -3) (-7, -9) (-13, -17)	(-19, -10) (6, -15) (14, -9)	(10, 15) (-14, -13) (-17, -9)	(16, 8) (-11, 4) (-15, 1)	(19, -1) (-4, -7) (-16, -16)
Варианты	60	70	80	90	00
А(x₁;y₁;) В(x₂;y₂;) С(x₃;y₃;)	(4, -8) (-9, -4) (-13, -7)	(-19, -7) (-5, -15) (4, -3)	(-6, 6) (-4, 0) (5, -12)	(19, -4) (13, 8) (17, 5)	(-10, 4) (-18, 5) (-10, -1)

3. Даны координаты вершин пирамиды А₁А₂А₃А₄. Средствами векторной алгебры найти:

1) угол между ребрами А₁А₂ и А₁А₄;

2) площадь грани А₁А₂А₃;

3) объем пирамиды А₁А₂А₃А₄;

4) уравнение плоскости основания пирамиды А₂А₃А₄;

5) уравнение высоты пирамиды, проведенной из вершины А₁.

Варианты	10	20	30	40	50
	(7, 2, -9) (3,-5,-5) (7,-8,-9) (1, 5, -7)	(6,-4,-5) (6,-7,-9) (-2, 2,-5) (6, 3, -5)	(3, 3, 6) (1, 3, 6) (1,-3, 3) (10,-1,10)	(-6, -7, 1) (-3, -5, 7) (1, -1, 7) (-6, -7, 6)	(3, 3, -5) (4, 5, -7) (9, 6, -3) (-4, -3, 1)
Варианты	60	70	80	90	00
	(-7, 8, 2) (-1, 5, 4) (-5, 10, 1) (-7, 8, 1)	(2, 4, 4) (-4,-3, -2) (5, 2, -2) (-2, -4, 5)	(-2, -1,-7) (2,-1,-7) (-2,-1, -6) (-4,-3,-8)	(1, 5, -1) (10, 3, 5) (1, 5, -9) (7, 5, -1)	(-1, 5, 5) (-3, 6, 3) (-1, 5, 2) (6, 9, 1)

4. 1) Составить уравнение поверхности, образованной вращением линии вокруг оси ОZ.

2) Подобрать значение параметра p так, чтобы точка А(x₀;y₀;z₀) лежала на поверхности.

3) Сделать схематический чертёж.

Варианты	Данные	задачи
	Уравнение линии в плоскости х = 0	А(x₀;y₀;z₀)
10	рy² = z	(1, 0,-1)
20	рy² + 2z² = 2	(1,-1, 0)
30	y² = рz² +р	(1, 3, 2)
40	y² + рz² = 6р	(1, 2, -1)
50	рy² + z² = 6	(1,-1, 2)
60	y² = z² + р	(4, 3, 5)
70	рy² = рz + 4	(1,-2, 1)
80	рy² + z² = 4р	(2, 1,-2)
90	рy² + z² = 4	(0, 1, 1)
00	y² + z² = 6р	(2, -1, 1)

Вариант 1

1. Решить систему линейных уравнений матричным методом и по формулам Крамера

Варианты		Варианты
01	3x + 4y - 2z = 1 x + 5y + z = 0 2x + 4y + 3z = 8	51	2x - 5y + z = 1 4x + 2y - 3z = 1 x - y + z = 2
11	3x + 2y + z = 1 2x - 3y + 2z = 9 x - 8y - 5z = -7	61	3x + 3y - 2z = 4 5x - 7y + 4z = 0 x + 2y - z = 3
21	2x - y - z = 0 2x + 4y - z = 15 3x - z = 5	71	x + 2y - 2z = 3 5x + 4y - 3z = 4 3x + y - 4z = 7
31	x + 2y - 3z = -3 2x - 3y + z = - 13 3x + y + 2z = 4	81	5x - y + 8z = 7 2x + 2y - 3z = 9 x + 3y + 2z = 1
41	x - 2y + 2z = -14 2x - y + z = -4 4x + y + 2z = 7	91	2x - 3y - 4z = -1 x + y + 5z = 0 3x + 2y + 4z = 8

2. Даны координаты вершин треугольника АВС. Требуется:

1) вычислить длину стороны ВС;

2) составить уравнение стороны ВС;

3) вычислить длину высоты, проведенной из вершины А;

4) составить уравнение этой высоты.

Варианты	01	11	21	31	41
А(x₁;y₁;) В(x₂;y₂;) С(x₃;y₃;)	(-4. 3) (-10, 6) (2, -10)	(-16, 13) (14, 3) (20, 11)	(10, 11) (-6, 14) (-2, 17)	(4, 9) (-9,-2) (-18, 10)	(8,-5) (-7,-10) (9, 2)
Варианты	51	61	71	81	91
А(x₁;y₁;) В(x₂;y₂;) С(x₃;y₃;)	(-10, 20) (-5,-5) (-15, 19)	(17,-19) (9, 15) (-15, 19)	(10,-6) (-3,-6) (7, 18)	(10,-16) (1,-18) (-11,-9)	(11,-15) (-3, 8) (1, 5)

3. Даны координаты вершин пирамиды А₁А₂А₃А₄. Средствами векторной алгебры найти:

1) угол между ребрами А₁А₂ и А₁А₄;

2) площадь грани А₁А₂А₃;

3) объем пирамиды А₁А₂А₃А₄;

4) уравнение плоскости основания пирамиды А₂А₃А₄;

5) уравнение высоты пирамиды, проведенной из вершины А₁.

Варианты	01	11	21	31	41
А₁(x₁;y₁;z₁) А₂(x₂;y₂;z₂) А₃(x₃;y₃;z₃) А₄(x₄;y₄;z₄)	(3, 1,-3) (3,-6,-3) (9,-6,-9) (2,-3, 5)	(-2,-4,-7) (-6,-8,-9) (-2, 1,-7) (-2,-8,-4)	(-1, 4,-4) (-4, 4,-8) (-9, 8,-3) (-5, 5, 4)	(4,-7, 8) (8,-3, 10) (2,-3, 4) (-2, 1, 8)	(-1,-3,-1) (1,-6,-7) (7,-9,-1) (1, 3, 8)
Варианты	51	61	71	81	91
А₁(x₁;y₁;z₁) А₂(x₂;y₂;z₂) А₃(x₃;y₃;z₃) А₄(x₄;y₄;z₄)	(5, 3, 1) (5, 3,-4) (-1,-6,-1) (-4, 1, 7)	(-2,-10,-1) (-1,-8, 1) (-6,-3, 3) (-5,-4, 1)	(2,-5,-7 ) (-4,-3, 2) (-2,-1,-9) (-6, 1,-7)	(8, 3,-5) (6, 7,-1) (8, 3,-10) (2,-3,-2)	(-1, 8, 3) (1, 8, 3) (-1, 4, 6) (1,-1,-3)

4. Построить поверхность, определяемую заданным уравнением

Вариант	Уравнение поверхности
01	x²+2x +2y² +4y -z² = 0
11	x² –4x + 4y² –8y + z² = 0
21	0,5x² +0,25y² –2z +2 = 0
31	x²–2x+y²–4y +z²–6z = 0
41	x²–6x +y²–2y–z² –4z = 0
51	x² + y² –2х – 4y = 0
61	x² – 4x – y² – 2y = 0
71	x² – 4x + 2z = 0
81	x² -3x -y² + 4y -2z² = 0
91	x² – 4x +y² – 2y – z = 0

Вариант 2

1. Решить систему линейных уравнений методом Гаусса

Варианты		Варианты
02	3x + 2z + u = –5 –4x–3y +5z–2u =–1 –2x–4y+6z+u = 4 –x–3y+ 7z – u =–6	52	x–3y + 4z +2u = –3 –y –5z –3u = 5 2x +2y –z +u = –2 2x +y –6z –2u = 4
12	2y +3z –u = 9 –2x –6y +z +2u =–2 –2x –5y –3z +u =–8 –2x –4y +4z +u = 8	62	–2x +4y +4z +u =–4 5x –5y –3z +u = –3 3y +3z +u = –2 –2x +7y+7z+4u =–6
22	–x +3y +2z+3u = –7 –4x +6y –6z –2u =8 –2x +5y –u = 3 –6x+11y–6z–3u=11	72	6x –3y –6z –3u = 6 –3x –4y +6z –u = 6 6x +4y –4z +2u = 4 3x +2z + u = 9
32	4x +4y –z –2u = 5 –3y +3z –u = 5 –2x –y –z –u = –7 4x +y +2z –3u = 11	82	–5x+2y +4z+3u =–3 –3x –4y +6z –u = 6 4x –5y –3z –3u = 5 x –9y +2z –5u = 6
42	6x +y –z +u = –8 5x +4y +z –3u = 4 –x –2y +4z +2u = 5 11x +5y –2u = –4	92	4x –2y +z +2u = –7 –3x –5y –z –2u =–9 y –6z +3u = 6 –3x –2y–7z +u = –2

2. Даны координаты вершин треугольника АВС. Требуется:

1) вычислить длину стороны ВС;

2) составить уравнение стороны ВС;

3) вычислить длину высоты, проведенной из вершины А;

4) составить уравнение этой высоты.

Варианты	02	12	22	32	42
А(x₁;y₁;) В(x₂;y₂;) С(x₃;y₃;)	(20, -7) (-19, 15) (-7,-1)	(0, 4) (7,-10) (15,-16)	(-12, 19) (3, 3) (15,-2)	(-18, 8) (12, 8) (16, 11)	(17, 18) (8, 11) (-7,-9)
Варианты	52	62	72	82	92
А(x₁;y₁;) В(x₂;y₂;) С(x₃;y₃;)	(-14, 1) (-7,-10) (-3,-7)	(14,-9) (-10,-12) (0, 12)	(-18, 20) (0, 9) (-12,-7)	(14, 3) (15, -2) (-9,-12)	(-4,-9) (15,-12) (12,-16)

3. Даны координаты вершин пирамиды А₁А₂А₃А₄. Средствами векторной алгебры найти:

1) угол между ребрами А₁А₂ и А₁А₄;

2) площадь грани А₁А₂А₃;

3) объем пирамиды А₁А₂А₃А₄;

4) уравнение плоскости основания пирамиды А₂А₃А₄;

5) уравнение высоты пирамиды, проведенной из вершины А₁.

Варианты	02	12	22	32	42
А₁(x₁;y₁;z₁) А₂(x₂;y₂;z₂) А₃(x₃;y₃;z₃) А₄(x₄;y₄;z₄)	(2,-5, 2) (-4,-3,-7) (-2, 2, 6) (4, 1, 5)	(2,-3, 2) (-2,-3, 5) (8,-1, 5) (-5,-9,-4)	(4, 4,-7) (4,-2, 1) (10,1,-5) (4,-7,-7)	(-4, 5,-7) (2, 5, 1) (-4, 9,-7) (-5, 3,-9)	(-1, 8,-9) (8, 2,-7) (8, 8,-9) (-1, 7,-9)
Варианты	52	62	72	82	92
А₁(x₁;y₁;z₁) А₂(x₂;y₂;z₂) А₃(x₃;y₃;z₃) А₄(x₄;y₄;z₄)	(-3, 4, 2) (5, 3, 6) (3, 10, 9) (5, 3,-2)	(5, 5, 2) (3, 5, 2) (6, 1, 10) (5, 5,-7)	(-3,10,-2) (-5, 8,-1) (5, 9,-6) (3, 3, 4)	(5, 4, 1) (6, 4, 1) (5, 4, 4) (3, 7, 7)	(1,-4, 3) (2,-4, 3) (8, 2, 9) (1,-4, 7)

4. 1) Составить уравнение поверхности, образованной вращением линии вокруг оси ОХ.

2) Подобрать значение параметра p так, чтобы точка А(x₀;y₀;z₀) лежала на поверхности.

3) Сделать схематический чертёж.

Варианты	Данные	задачи
	Уравнение линии в плоскости y = 0	А(x₀;y₀;z₀)
02	px –2 = z²	(2;-2; 2)
12	x + p = z²	(1; 3; 2)
22	px² = z²	(1; 0; -1)
32	px = z²	(2; -2; 2)
42	px² = z² – 4	(2; -5; 1)
52	5x² + pz² = 10	(2; 3; 3)
62	p – x² = z²	(2; 1; 1)
72	px² + z² = 4	(0; 1; 1)
82	px² + z² = 0	(1;-2; 1)
92	px + 4 = z²	(1;-1; 2)

Вариант 3

1. Решить систему линейных уравнений матричным методом и по формулам Крамера

Варианты		Варианты
03	x +2y –2z = –1 –3x +2y +4z = –9 3x –4y –z = 7	53	–3x –2y +3z = –5 –3x +2y – z = –9 5x –3y –3z = 6
13	2x +y +4z = 5 –3x –y +2z = 2 –x – 4z = –3	63	6x +3y = 9 5x +2y +2z = 9 –5x +4y –5z = –6
23	–5x –3y +6z = –2 5x +3y –4z = 4 –6x –2y +3z = –5	73	3x –6y –3z = 9 4x +5y –3z = –3 –x –4y +6z = –7
33	–x +4y +z = –8 4x –4y +3z = 1 –2x +5y –3z = –5	83	4x +3y –4z = 1 –6x –3y +3z = –6 –y –z = 0
43	5x +2y +4z = 8 5x +y +3z = 7 3x –2y –2z = 4	93	5x + y = 6 5x +3y +3z = –1 –x –4y –4z = 7

2. Даны координаты вершин треугольника АВС. Требуется:

1) вычислить длину стороны ВС;

2) составить уравнение стороны ВС;

3) вычислить длину высоты, проведенной из вершины А;

4) составить уравнение этой высоты.

Варианты	03	13	23	33	43
А(x₁;y₁;) В(x₂;y₂;) С(x₃;y₃;)	(-11, 0) (4, 0) (-5, 12)	(4, -16) (-14,-17) (-19,-5)	(8, 4) (-2, 14) (2,17)	(12, 17) (9, 1) (13, 4)	(18, 17) (-5, 16) (-13, 10)
Варианты	53	63	73	83	93
А(x₁;y₁;) В(x₂;y₂;) С(x₃;y₃;)	(3, -2) (0, 20) (15, 12)	(-3,-2) (19, 18) (3,-12)	(7, 2) (2, 7) (14, 16)	(-5, 2) (1,-20) (-19,-5)	(16, 13) (20,-20) (-4,-2)

3. Даны координаты вершин пирамиды А₁А₂А₃А₄. Средствами векторной алгебры найти:

1) угол между ребрами А₁А₂ и А₁А₄;

2) площадь грани А₁А₂А₃;

3) объем пирамиды А₁А₂А₃А₄;

4) уравнение плоскости основания пирамиды А₂А₃А₄;

5) уравнение высоты пирамиды, проведенной из вершины А₁.

Варианты	03	13	23	33	43
А₁(x₁;y₁;z₁) А₂(x₂;y₂;z₂) А₃(x₃;y₃;z₃) А₄(x₄;y₄;z₄)	(2, -1, 2) (8,-8,-4) (-1,-7,4) (8,-7,-5)	(-5, 2, 1) (-1, 3,-7) (-9,-6, 2) (-7, 5,-5)	(-6, 8, 2) (-2, 6,-2) (-6, 4,-1) (-4, 8, 2)	(-3,-2,-3) (5,-6,-4) (-7, 2, 4) (-9, 1,-5)	(8, 3, 3) (6,-3, 6) (2, 9,-4) (4,-5, 2)
Варианты	53	63	73	83	93
А₁(x₁;y₁;z₁) А₂(x₂;y₂;z₂) А₃(x₃;y₃;z₃) А₄(x₄;y₄;z₄)	(-4, 3,-1) (-6, 4,-3) (-4, 3,9) (-4, 7,-1)	(3,-1,2) (7, 6, 6) (1, 3, 6) (4,-5,-6)	(-2, 3, 3) (-1, 5, 1) (-8, 5, 6) (-8, 6, 5)	(-1,-1,-3) (-6,-1,-3) (3,-9,-4) (2, 5,-1)	(-5,-5, 1) (-5,-5, 9) (-7,-9, 5) (2, 1,-5)

4. Построить поверхность, определяемую заданным уравнением

Варианты	Уравнение поверхности
03	x² +2x +y² –2y –2z = 2
13	4x² –8x –9y² –36y –72z² = –184
23	x² -6x + 4y² +16y + 9 = 0
33	x² + y² –2z = 1
43	x +y² = 4
53	x² -4x +y² +2y = z
63	4x² –4x –9y² –6y = z
73	x²+6x+2y²–18y–8z = –49
83	6y +4z +20 = z²
93	y² +z² + 2z = 0

Вариант 4

1. Решить систему линейных уравнений методом Гаусса

Варианты		Варианты
04	2x -y + 3z -2u = 1 x - z + 2u = 6 x + y - z + u = 4 3x - y + z - u = 0	54	4x +2y +3z +2u = 5 3x +3y +5z -u = 3 -5x -6y -6z-u = -9 -2x-3y -z -2u = -6
14	3x + 2z + u = –5 –4x–3y +5z–2u =–1 –2x–4y+6z+u = 4 –x–3y+ 7z – u =–6	64	4x +4y –z –2u = 5 –3y +3z –u = 5 –2x –y –z –u = –7 4x +y +2z –3u = 11
24	–x +3y +2z+3u = –7 –4x +6y –6z –2u =8 –2x +5y –u = 3 –6x+11y–6z–3u=11	74	-4x+5z +2u = 9 -4x -y –4z -2u =-8 -x +3y -5z +u = -6 -4x -5y +z = 1
34	2y +3z –u = 9 –2x –6y +z +2u =–2 –2x –5y –3z +u =–8 –2x –4y +4z +u = 8	84	x–3y + 4z +2u = –3 –y –5z –3u = 5 2x +2y –z +u = –2 2x +y –6z –2u = 4
44	-4x-2y-5z +u = -3 -2x +6y +4z +u = 0 4x -y +6z -2u = -3 -3y +z -u = -6	94	x +y -4z +2u = 7 2x -6y +2u = -8 -x -5y -5z +u = -9

2. Даны координаты вершин треугольника АВС. Требуется:

1) вычислить длину стороны ВС;

2) составить уравнение стороны ВС;

3) вычислить длину высоты, проведенной из вершины А;

4) составить уравнение этой высоты.

Варианты	04	14	24	34	44
А(x₁;y₁;) В(x₂;y₂;) С(x₃;y₃;)	(-17,-9) (-3,-6) (3,-14)	(12,-13) (-13, 12) (-19, 20)	(-3, 11) (11, 8) (-7,-16)	(0,11) (13, 12) (10, 16)	(-7, 6) (20,-3) (14,-11)
Варианты	54	64	74	84	94
А(x₁;y₁;) В(x₂;y₂;) С(x₃;y₃;)	(5, 12) (-5,-8) (7, 1)	(15,-19) (17, 20) (-19,-7)	(19, 1) (-17, 3) (19,-12)	(6,-16) (4, 13) (0, 16)	(1, 4) (14,-9) (19, 3)

3. Даны координаты вершин пирамиды А₁А₂А₃А₄. Средствами векторной алгебры найти:

1) угол между ребрами А₁А₂ и А₁А₄;

2) площадь грани А₁А₂А₃;

3) объем пирамиды А₁А₂А₃А₄;

4) уравнение плоскости основания пирамиды А₂А₃А₄;

5) уравнение высоты пирамиды, проведенной из вершины А₁.

Варианты	04	14	24	34	44
А₁(x₁;y₁;z₁) А₂(x₂;y₂;z₂) А₃(x₃;y₃;z₃) А₄(x₄;y₄;z₄)	(-2,-1,2) (1,-7, 4) (-2, 2, 6) (-4, 8, 8)	(-3,-6,-5) (-9,-9, 1) (5,-2,-6) (-5,-8,-4)	(-3,-7,-6) (3,-5, 3) (-1,-1,-3) (-9,-5,-9)	(2,-7,-3) (8,-7, 5) (-4,-10,-9) (-6,-7, 3)	(-4, 1,-2) (-4,-3,-2) (-7, 3, 4) (-5, 1,-2)
Варианты	54	64	74	84	94
А₁(x₁;y₁;z₁) А₂(x₂;y₂;z₂) А₃(x₃;y₃;z₃) А₄(x₄;y₄;z₄)	(2, 1,-8) (1, 1,-8) (4,-2,-2) (8,-1,-5)	(2, 1,-5) (2, 5,-5) (-2, 5, 2) (-4,-1,-2)	(-4,-6,-3) (2,-9,-9) (-2,-4,-2) (-1,-4,-9)	(9,-1,-5) (6, 5, 1) (5,-4,-5) (7, 3,-9)	(-4,-5, 4) (-4,-5,-8) (-5,-7, 2) (5,-7, -2)

4. 1) Составить уравнение поверхности, образованной вращением линии вокруг оси ОZ.

2) Подобрать значение параметра p так, чтобы точка А(x₀;y₀;z₀) лежала на поверхности.

3) Сделать схематический чертёж.

Варианты	Данные	задачи
	Уравнение линии в плоскости Х = 0	А(x₀;y₀;z₀)
04	y ² - 2 = z ²	(3; -2; 3)
14	рy ² + z² = 4	(1; 2; 1)
24	у ² + 2 = pz ²	(1; 0; 1)
34	рy² = z ²	(2; 2; -2)
44	p + y² = z ²	(-1; 1; 2)
54	5y ²+ pz ² = 10	(-1; 1; -1)
64	у ² + z ² = p	(-2; 1; 1)
74	рy ² + z ² = 4	(-1; 1; 0)
84	рy ² = z ²	(3; 2; 3)
94	рy ² +4 = z ²	(-5; 2; 1)

Вариант 5

1. Решить систему линейных уравнений методом Гаусса

Варианты		Варианты
05	-x -5y +2u = -4 4x +y -3z -u = -2 x +4y +4z +u = 0 -y +4z +3u = -4	55	-3x -5y -z -3u = 8 -5x +y -4z -u = 5 -4x +y -4z -u = 4 -7x-4y-5z-4u = 12
15	5y -z +3u = 9 -x -y -4z +u = 6 2x -2y -2z -2u = 0 -x+4y-5z+4u =-15	65	3x +y +u = -9 x +3y -z +2u = -3 x +3y -z +2u = -3 4x +4y-z +3u = -12
25	4x -4y -z +u = -4 -3x+2y-3z+2u =-9 -5x +2y +2u = -1 x-2y -4z +3u = -13	75	2x -z +2u = -9 -3x+4y+6z+2u =-5 -2x +4y +4z -u = 0 -5x+8y+10z+u =-5
35	-3x -y +z +2u = 7 -4x -3y -3z-u = -8 -3x-2y +2z -2u = 2 -7x-4y-2z +u = -1	85	2x +y -2z -u = 0 -2x -3y +2 u = -1 -3x-2y+2z +u = -2 -2y -2z +u = -1
45	4x -2y +4z -u = 0 x +3y +4z +2u = -2 -x +5y +z -2u = 6 5x +y +8z +u = -2	95	-3x+3y-2z+2u =-3 -x -2y +4z -2u = 6 2x +3y -5z -u = -7 x +y -z -3u = -1

2. Даны координаты вершин треугольника АВС. Требуется:

1) вычислить длину стороны ВС;

2) составить уравнение стороны ВС;

3) вычислить длину высоты, проведенной из вершины А;

4) составить уравнение этой высоты.

Варианты	05	15	25	35	45
А(x₁;y₁;) В(x₂;y₂;) С(x₃;y₃;)	(19, 7) (16, 18) (10, 10)	(13,-3) (-10, 8) (2, 13)	(1,-2) (3,-18) (-9,-13)	(-15, 11) (-18,-11) (12, 5)	(19,-4) (-6,-19) (-9,-15)
Варианты	55	65	75	85	95
А(x₁;y₁;) В(x₂;y₂;) С(x₃;y₃;)	(-11, 3) (15, 10) (-5, -5)	(-2, -19) (2, -7) (-6, -1)	(-18, 17) (5, 16) (-10,-4)	(17, 0) (-2,-18) (-11,-6)	(-14, 4) (-15, 7) (-3, 16)

3. Даны координаты вершин пирамиды А₁А₂А₃А₄. Средствами векторной алгебры найти:

1) угол между ребрами А₁А₂ и А₁А₄;

2) площадь грани А₁А₂А₃;

3) объем пирамиды А₁А₂А₃А₄;

4) уравнение плоскости основания пирамиды А₂А₃А₄;

5) уравнение высоты пирамиды, проведенной из вершины А₁.

Варианты	05	15	25	35	45
А₁(x₁;y₁;z₁) А₂(x₂;y₂;z₂) А₃(x₃;y₃;z₃) А₄(x₄;y₄;z₄)	(9,-3,3) (2,3,9) (-2,-3,3) (7,-7,7)	(2,-5,1) (-4,-3,10) (2,-5,-5) (-4,-8,-1)	(3,5,-5) (7,-3,-6) (-3, 8, 1) (9,-1,-2)	(-5, 5, 4) (-5, 5,-4) (-7, 9, 8) (-3,-4,-2)	(8,-4, 3) (8,-7, 3) (8,-4, 6) (5, 2,-3)
Варианты	55	65	75	85	95
А₁(x₁;y₁;z₁) А₂(x₂;y₂;z₂) А₃(x₃;y₃;z₃) А₄(x₄;y₄;z₄)	(-2,-2,-2) (-3,-4,-4) (-2,-6,-2) (-2,-6,-5)	(-5,-3,-1) (2, 1, 3) (-6, 1, 7) (-4,-7, 7)	(1, 2, 6) (-5,-4, 3) (-1, 4, 7) (9, 6, 7)	(-1,-5, 9) (1,-9, 5) (-7,-8, 3) (1,-4, 7)	(-7, 4,-7) (-7, 4,-1) (-3,-4,-6) (-1,-2,-4)

4. Построить поверхность, определяемую заданным уравнением

Вариант	Уравнение поверхности
05	-4x +y² -6y + 17 = 0
15	у ² - 2y + z² = 0
25	x²-6x+4y²+9z²+36z= 99
35	16x²+3y² +16z² -48 = 0
45	2x² +y² +4y +2z² = 4x-4z-7
55	x² -9y² -3z² = 0
65	х² +4y² -2z² = 0
75	x²+2x+2y²+4y+4z²+1= 0
85	x² +y² +2z² -2 -4z = 0
95	9x²-18x+16y²+64y+36z²-216z +253= 0

Вариант 6

1. Решить систему линейных уравнений матричным методом и по формулам Крамера

Варианты		Варианты
06	x -4y +z = 4 -3x + z = 8 -6x -y -4z = 5	56	5x -5y +3z = -9 5x +3y = 8 x -4y -3z = 6
16	3y +3z = -6 5x -5y -z = -4 2x -y +5z = -8	66	-2x +4y +z = -5 -2x -6y -z = -3 3x -3y +z = -7
26	x -2y +2z = -1 x -y -z = 1 -2x -4y -3z = 9	76	-3x +6y -5z = -5 -4x -5y +z = -9 -4x -2z = -8
36	-6x +3y -5z = 8 -5x -3y +z = 6 -5x -2y -5z = -4	86	-2x +4y -2z = -4 4x +3y -3z = 4 -x +2y -6z = 3
46	4x +5y -z = 4 x -y +2z = 1 5x +5y +4z = 1	96	y +5z =-7 -4x -5y +3z = -5 -6x -5y -5z = -3

2. Даны координаты вершин треугольника АВС. Требуется:

1) вычислить длину стороны ВС;

2) составить уравнение стороны ВС;

3) вычислить длину высоты, проведенной из вершины А;

4) составить уравнение этой высоты.

Варианты	06	16	26	36	46
А(x₁;y₁;) В(x₂;y₂;) С(x₃;y₃;)	(-2,-10) (3, 10) (0, 6)	(3,-6) (-8,-4) (10, 20)	(9,-2) (-1,-17) (-6,-5)	(13, 8) (19, 5) (15, 2)	(-7, 5) (8,-11) (13, 1)
Варианты	56	66	76	86	96
А(x₁;y₁;) В(x₂;y₂;) С(x₃;y₃;)	(-6,-19) (-7,-17) (11, 7)	(-16,-7) (7,-16) (-5, 0)	(7, 9) (2, -6) (-4,-14)	(5,-18) (10,-13) (-2,-4)	(6,-3) (15,-1) (6,-13)

3. Даны координаты вершин пирамиды А₁А₂А₃А₄. Средствами векторной алгебры найти:

1) угол между ребрами А₁А₂ и А₁А₄;

2) площадь грани А₁А₂А₃;

3) объем пирамиды А₁А₂А₃А₄;

4) уравнение плоскости основания пирамиды А₂А₃А₄;

5) уравнение высоты пирамиды, проведенной из вершины А₁.

Варианты	06	16	26	36	46
А₁(x₁;y₁;z₁) А₂(x₂;y₂;z₂) А₃(x₃;y₃;z₃) А₄(x₄;y₄;z₄)	(3, 5, 5) (3, 5, 10) (9,-4, 3) (-7, 5, 5)	(-4,-2,-5) (-6,-1,-3) (-4,-5,-1) (-6, 4,-2)	(3, 3,-7) (5, 9, 2) (-3,5,-4) (9,9,-10)	(-5, 4,-7) (-3,-5,-1) (3,-4,-3) (1, 7,-1)	(-3,-1,-5) (-1,-7,-8) (-7, 7, 3) (-4,-3,-3)
Варианты	56	66	76	86	96
А₁(x₁;y₁;z₁) А₂(x₂;y₂;z₂) А₃(x₃;y₃;z₃) А₄(x₄;y₄;z₄)	(-8, 9,-5) (-2, 3, 2) (-4, 9,-2) (-8, 6,-9)	(-2,-5,-5) (1,-9,-5) (-2, 7,-5) (4, 1,-2)	(-1, 3,-8) (-7, 5, 1) (-3, 2,-6) (-3, 6,-2)	(-7,-6,-7) (5,-6,-7) (-7,-9,-7) (-3,-6,-4)	(3,-6,-6) (7, 2, 2) (5,-10,-2) (-3,-8,-3)

4. 1) Составить уравнение поверхности, образованной вращением линии вокруг оси ОУ.

2) Подобрать значение параметра p так, чтобы точка А(x₀;y₀;z₀) лежала на поверхности.

3) Сделать схематический чертёж.

Варианты	Данные	задачи
	Уравнение линии в плоскости х = 0	А(x₀;y₀;z₀)
06	у = рz²	(-1; 5; 2)
16	2y² + рz² = 2	(1; 0; -1)
26	рy² + р = z²	(2; 3; 1)
36	y² + рz² = 6р	(1; -1; 2)
46	y² + рz² = 6	(2; -1; 2)
56	y²+ р = z²	(4; 5; 3)
66	рy +4 = рz²	(1; 1; 2)
76	y² + рz² = 4р	(2; -2; 1)
86	y² + рz² = 4	(-2; 1 –1)
96	y² + z² = 6р	(2; 1; -1)

Вариант 7

1. Решить систему линейных уравнений методом Гаусса

Варианты		Варианты
07	4x -2y +4z -u = 0 x +3y +4z +2u = -2 -x +5y +z -2u = 6 5x +y +8z +u = -2	57	2x +y -2z -u = 0 -2x -3y +2 u = -1 -3x-2y+2z +u = -2 -2y -2z +u = -1
17	x +y -4z +2u = 7 2x -6y +2u = -8 -x -5y -5z +u = -9	67	-3x+3y-2z+2u =-3 -x -2y +4z -2u = 6 2x +3y -5z -u = -7 x +y -z -3u = -1
27	-3x+3y-2z+2u =-3 -x -2y +4z -2u = 6 2x +3y -5z -u = -7 x +y -z -3u = -1	77	4x -4y -z +u = -4 -3x+2y-3z+2u =-9 -5x +2y +2u = -1 x-2y -4z +3u = -13
37	-4x+5z +2u = 9 -4x -y –4z -2u =-8 -x +3y -5z +u = -6 -4x -5y +z = 1	87	4x +2y +3z +2u = 5 3x +3y +5z -u = 3 -5x -6y -6z-u = -9 -2x-3y -z -2u = -6
47	-3x -y +z +2u = 7 -4x -3y -3z-u = -8 -3x-2y +2z -2u = 2 -7x-4y-2z +u = -1	97	2x -z +2u = -9 -3x+4y+6z+2u =-5 -2x +4y +4z -u = 0 -5x+8y+10z+u =-5

2. Даны координаты вершин треугольника АВС. Требуется:

1) вычислить длину стороны ВС;

2) составить уравнение стороны ВС;

3) вычислить длину высоты, проведенной из вершины А;

4) составить уравнение этой высоты.

Варианты	07	17	27	37	47
А(x₁;y₁;) В(x₂;y₂;) С(x₃;y₃;)	(-8, 9) (-15, 0) (-12,-4)	(3, 10) (-15, 1) (5,-14)	(-18,-15) (-7,-17) (14, 11)	(-12,-9) (-2,-9) (-5.-5)	(-12, 5) (14, 7) (5, 19)
Варианты	57	67	77	87	97
А(x₁;y₁;) В(x₂;y₂;) С(x₃;y₃;)	(9,-3) (1, 9) (13, 4)	(14,-4) (-11,-12) (-6, 0)	(5,-16) (-9,-13) (-1, -19)	(3,-20) (-7, 5) (-10, 9)	(4,-9) (-6, 11) (0, 3)

3. Даны координаты вершин пирамиды А₁А₂А₃А₄. Средствами векторной алгебры найти:

1) угол между ребрами А₁А₂ и А₁А₄;

2) площадь грани А₁А₂А₃;

3) объем пирамиды А₁А₂А₃А₄;

4) уравнение плоскости основания пирамиды А₂А₃А₄;

5) уравнение высоты пирамиды, проведенной из вершины А₁.

Варианты	07	17	27	37	47
А₁(x₁;y₁;z₁) А₂(x₂;y₂;z₂) А₃(x₃;y₃;z₃) А₄(x₄;y₄;z₄)	(3; 2; 2) (3; 5;-2) (2;-6; 6) (9; 8; 5)	(2; 8; 4) (-2; 4; 6) (8; 5;-2) (2; 8;-7)	(-1;-7; 3) (3;-5;-1) (1;-10; 9) (5; 2; 1)	(6; 7; 10) (8; 10; 7) (7; 6;-1) (-3; 4; 5)	(-2;-4; 6) (4;-6;-3) (2;-6; 2) (2;-5;-2)
Варианты	57	67	77	87	97
А₁(x₁;y₁;z₁) А₂(x₂;y₂;z₂) А₃(x₃;y₃;z₃) А₄(x₄;y₄;z₄)	(-7; 3;-10) (2; 5;-4) (-4; 9;-8) (-3;-1;-3)	(-4;-3;-1) (-3; 1;-9) (-4;-3; 9) (-6;-2; 1)	(-7; 2;-1) (1;-6;-5) (-1; 9; 5) (-7; 2;-5)	(4;-2; 2) (8;-2; 2) (-2;-9; 8) (4; 4; 2)	(3;-4; 2) (7;-2;-2) (5;-5; 4) (-3; 2; 5)

4. Построить поверхность, определяемую заданным уравнением

Варианты	Уравнение поверхности
07	x² -2x +2y² -8y +3z² +6z =10
17	x² -8x + y² + 10y +z² -12z -4 = 0
27	8x² - 4y² +2z² - 48 = 0
37	3x² +24x -4y² -8y +6z² -36z + 122 = 0
47	-x² -4x +2y² +4y +3z² -24z +52 = 0
57	2x² -12x +2y² -10y +2z² +8z +1 = 0
67	x² -2x +y² -4y +z² -4 = 0
77	4x² +16x -9y²-54y +36z² -72z -65 = 0
87	2x²-12x -6y²-24y +3z² -24z +30 = 0
97	x²+8x-6y²+12y +3z² +1 = 0

Вариант 8

1. Решить систему линейных уравнений методом Гаусса

Варианты		Варианты
08	x -y +3z +2u = 9 -x +5y -z +2u = 7 x -4y -3z +3u = -8	58	-4x+5z +2u = 9 -4x -y –4z -2u =-8 -x +3y -5z +u = -6 -4x -5y +z = 1
18	-6x +3y +3u = 3 -5x+2y+4z-3u =-8 5x -y -2z -2u = -2 -11x +5y +4z = -2	68	5x -2y +3z -u = 8 4x + 2z -u = 9 -x +5y -5z -u = 2
28	2x +2y -3z +u = 3 -x -4y -5z -u = 7 x +4y -u = 9 -5z -2u = 16	78	4x +2y +3z +2u = 5 3x +3y +5z -u = 3 -5x -6y -6z-u = -9 -2x-3y -z -2u = -6
38	x +y -4z +2u = 7 2x -6y +2u = -8 -x -5y -5z +u = -9	88	-5x -y -3z -u = 7 -2x +5y -2z +u = 1 y -3z -u = 0
48	4x -4y -3z -3u =-7 -2x+2y-4z -u = -8 -5x+2y-2z-2u =-6 2x-2y-7z-4u = -15	98	-4x-2y-5z +u = -3 -2x +6y +4z +u = 0 4x -y +6z -2u = -3 -3y +z -u = -6

2. Даны координаты вершин треугольника АВС. Требуется:

1) вычислить длину стороны ВС;

2) составить уравнение стороны ВС;

3) вычислить длину высоты, проведенной из вершины А;

4) составить уравнение этой высоты.

Варианты	08	18	28	38	48
А(x₁;y₁;) В(x₂;y₂;) С(x₃;y₃;)	(6, 12) (-16,-19) (8, 13)	(-17, 13) (-1, 20) (14, 0)	(18, 2) (-4, 3) (-16,-6)	(7, -9) (-5, 0) (10, 20)	(16, 1) (-18, -2) (-15,-6)
Варианты	58	68	78	88	98
А(x₁;y₁;) В(x₂;y₂;) С(x₃;y₃;)	(-13, 6) (-16, 7) (-7, 19)	(19, 3) (-13, -1) (-1,-17)	(19, -13) (-9, 4) (12,-16)	(-1, 13) (-3,-12) (-18,-4)	(-1, 7) (-9, 16) (18,-20)

3. Даны координаты вершин пирамиды А₁А₂А₃А₄. Средствами векторной алгебры найти:

1) угол между ребрами А₁А₂ и А₁А₄;

2) площадь грани А₁А₂А₃;

3) объем пирамиды А₁А₂А₃А₄;

4) уравнение плоскости основания пирамиды А₂А₃А₄;

5) уравнение высоты пирамиды, проведенной из вершины А₁.

Варианты	08	18	28	38	48
А₁(x₁;y₁;z₁) А₂(x₂;y₂;z₂) А₃(x₃;y₃;z₃) А₄(x₄;y₄;z₄)	(3, 2, 3) (1,-4,-6) (1, 6, 7) (9,-4,10)	(5, 5, 2) (5, 8, 2) (7, 1,-2) (7,-1,-1)	(-5,-2,-5) (2,-8, 1) (4,-2,-5) (-5, 4,-5)	(-1,-4, 5) (2,-4, 9) (-1,-4, 9) (-1, 2, 5)	(-9,-2,-5) (-2, 2,-9) (-8,-2,-5) (-9,-2, 6)
Варианты	58	68	78	88	98
А₁(x₁;y₁;z₁) А₂(x₂;y₂;z₂) А₃(x₃;y₃;z₃) А₄(x₄;y₄;z₄)	(-4,-7,-2) (-2,-1, 7) (-4,-7,-8) (-10,-9, 7)	(-3, 3, 5) (3, 9, 2) (3,-6, 7) (-1, 6,-1)	(3,-8, 7) (3,-8,-3) (5,-6, 6) (-3,-2, 4)	(5,-5,-1) (4, 3,-5) (3,-5,-1) (-1,-3,8)	(-2,-8,-3) (-6,-1,-7) (-2,-8,-2) (4,-6, 6)

4. 1) Составить уравнение поверхности, образованной вращением линии вокруг оси ОУ.

2) Подобрать значение параметра p так, чтобы точка А(x₀;y₀;z₀) лежала на поверхности.

3) Сделать схематический чертёж.

Варианты	Данные	задачи
	Уравнение линии в плоскости х = 0	А(x₀;y₀;z₀)
08	у + 1 = pz²	(1; 1; 2)
18	2y² + pz² = 2	(1; 0;-1)
28	py² + p = z²	(-1; 5; 2)
38	y² + pz² = 6p	(1;-1; 2)
48	y² + pz² = 6	(-2; 1; -1)
58	y² + p = z²	(4; 5; 3)
68	py + 4 = pz²	(2; 3; 1)
78	y² + pz² = 4p	(2;-2; 1)
88	y² + pz² = 4	(2;-1; -2)
98	y² + z² = 6p	(2; 1;-1)

Вариант 9

1. Решить систему линейных уравнений матричным методом и по формулам Крамера

Варианты		Варианты
09	-y -3z = 7 x +6y +z = -8 -4x +6y -z = -1	59	2x + z = 1 5x +5y +6z = 4 -5x +y -z = -3
19	5x -y = 9 2x -3y +z = -1 -4x +2y +z = -8	69	6x +2y +2z = 4 -2x +5y -5z = 6 -5x -y -5z = 6
29	-5x +2y +4z = -3 4x +6y = 8 x +6y +5z = -4	79	4x +4y +6z = -6 6x +3y -5z = 8 2x -3y -4z = 9
39	-x +3y +2z = -3 -3y -2z = 2 -x -6y -3z = 5	89	-5x +y -6z = 1 5y -2z = 8 6x -3y +3z = -9
49	-x +5y +z = -1 2x -6y +3z = 8 -3x +2y -5z = -6	99	-x -5y -2z = -4 x - 6y -3z = -2 -5x -3y -2z = -6

2. Даны координаты вершин треугольника АВС. Требуется:

1) вычислить длину стороны ВС;

2) составить уравнение стороны ВС;

3) вычислить длину высоты, проведенной из вершины А;

4) составить уравнение этой высоты.

Варианты	09	19	29	39	49
А(x₁;y₁;) В(x₂;y₂;) С(x₃;y₃;)	(14, -14) (11, 7) (14, 11)	(14, 17) (-3, 1) (9, 17)	(-14,-6) (9,-12) (6,-16)	(-18,-11) (-4, 7) (-16, -2)	(-11,-14) (17, 15) (2, -5)
Варианты	59	69	79	89	99
А(x₁;y₁;) В(x₂;y₂;) С(x₃;y₃;)	(12,-19) (14,-8) (18,-11)	(5, 14) (-3, -5) (-7, -2)	(6, 5) (-8, 2) (-14, 10)	(-6, 0) (-12,-2) (12, 16)	(12, 5) (4, -4) (-8, 5)

3. Даны координаты вершин пирамиды А₁А₂А₃А₄. Средствами векторной алгебры найти:

1) угол между ребрами А₁А₂ и А₁А₄;

2) площадь грани А₁А₂А₃;

3) объем пирамиды А₁А₂А₃А₄;

4) уравнение плоскости основания пирамиды А₂А₃А₄;

5) уравнение высоты пирамиды, проведенной из вершины А₁.

Варианты	09	19	29	39	49
А₁(x₁;y₁;z₁) А₂(x₂;y₂;z₂) А₃(x₃;y₃;z₃) А₄(x₄;y₄;z₄)	(-5; 4;2) (4;2;8) (-3;7;8) (3;5;-2)	(-3;-1;7) (-5;-5;3) (-3;-7;7) (1;3;5)	(10;-5;2) (4;2;-4) (2;-6;6) (6;-9;9)	(-5;6;-7) (1;4;-4) (1; 6; 1) (1; 3;-5)	(-7;-7; 1) (-7;-4;-3) (-3;-8;-7) (-10;-1;7)
Варианты	59	69	79	89	99
А₁(x₁;y₁;z₁) А₂(x₂;y₂;z₂) А₃(x₃;y₃;z₃) А₄(x₄;y₄;z₄)	(3; 1;-5) (3;1;-10) (5;-8; 1) (1; 4; 1)	(6;-1; 5) (3;-7; -1) (-2;-5; 4) (6;-3; 5)	(-3;-4;-1) (-6;-10;1) (-6;-4;-5) (1;-6; 3)	(-1; 1;-3) (-2; 5; 5) (-5;-3;-1) (-3; 4;-9)	(-6; 2;-3) (3; 2;-3) (-5;10;-7) (-4; 3;-5)

4. 1) Составить уравнение поверхности, образованной вращением линии вокруг оси ОZ.

2) Подобрать значение параметра p так, чтобы точка А(x₀;y₀;z₀) лежала на поверхности.

3) Сделать схематический чертёж.

Варианты	Данные	задачи
	Уравнение линии в плоскости у = 0	А(x₀;y₀;z₀)
09	x² = pz - 2	(-1; 1;-1)
19	x² = z + p	(1; 1;-2)
29	x² = pz²	(0; 1;-1)
39	x² = pz	(1; 2;-5)
49	x² - pz² = 4	(3;-2; 3)
59	px² + 5z² = 10	(1; 2; 1)
69	x² = p - z²	(1; 0; 1)
79	x² + pz² = 4p	(-2; 2;2)
89	x² + pz² = 0	(2; 1;-1)
99	x² = pz + 4	(3; 2; 3)

Учебно-методическое пособие

по курсу

ВЫСШАЯ МАТЕМАТИКА

Часть 1

ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ

Ордена Трудового Красного Знамени федеральное государственное

бюджетное образовательное учреждение высшего образования

Московский технический университет связи и информатики

Кафедра теории вероятностей и прикладной математики

Учебно-методическое пособие

по курсу

ВЫСШАЯ МАТЕМАТИКА

Часть 1

ЛИНЕЙНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

для студентов-заочников 1 курса

(направления: 11.03.02, 15.03.04)

1 семестр

Москва 2017

План УМД на 2017/18 уч.г.

Учебно-методическое пособие

по курсу

ВЫСШАЯ МАТЕМАТИКА

Часть 1

ЛИНЕЙНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

Составители: А.В. Власов, доцент

В.С. Юдин, доцент

Издание утверждено на заседании кафедры. Протокол № 8 от 20.04.17 г.

Рецензент А.Г. Кюркчан, профессор

ВВЕДЕНИЕ

«Линейная алгебра и аналитическая геометрия»;

«Высшая математика».

По этим курсам выполняются контрольные работы и сдается экзамен.

Настоящее учебно-методическое пособие и контрольная работа относятся к первой части курса.

Аудиторная работа		Самостоятельная работа		Итого
Лекции	Упражнения	Изучение курса	Выполнение контрольных работ
6	10	72	20	108

РАБОЧАЯ ПРОГРАММА

ОПРЕДЕЛИТЕЛИ

1. Определители и их основные свойства.

2. Системы линейных уравнений. Правило Крамера. Линейные однородные системы и их нетривиальные решения.

ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ

ВЕКТОРЫ

Дата: 2018-11-18, просмотров: 924.

12 3 4 5 6 7 8 9 Следующая ⇒