В случае, когда MathCAD не может найти решение, появляется сообщение об ошибке (элемент блока выделяется красным цветом). Причинами могут быть следующие:
- достигнута точка, из которой не может быть получено более точное приближение к решению;
- достигнута точка, из которой невозможно выбрать подходящее направление спуска, т.е. направление, вдоль которого ищется следующее приближение. В связи с этим продолжать итерации невозможно;
- достигнут предел точности вычислений. Дальнейшие вычисления не увеличивают точность решения вследствие влияния ошибок округления.
Для приближенного решения нелинейных уравнений применяется встроенная функция Minerr(), аналогичная по формату функции Find (). В качестве примера рассмотрим ее использование для решений окружности и прямой. Найдем точки их пересечения с помощью решающего блока Given – Minerr:
· Зададим точки начального приближения:
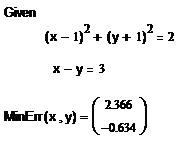
· Применим вычислительный блок Given – Minerr(). Данный вычислительный блок выдает решение в виде вектора, корни системы уравнений в данном случае имеют приближенное значение. Это связано с немого иным условием окончания методами приближения вычислительного блока Given – Minerr() по сравнению с блоком Given – Find(), который выдает точное решение системы. Уравнения в блоке Given – Minerr() записываются через жирное равно (Ctrl + =):

Использование функции Lsolve().
Для решения системы линейных уравнений, коэффициенты которых можно записать в виде матрицы А и свободные члены в виде вектора В, целесообразно использовать встроенную функцию lsolve ( A , B ). Она возвращает вектор неизвестных скалярных величин, удовлетворяющих данной системе линейных уравнений.
Формат функции: lsolve(Матрица системы, Вектор правых частей)
Например, дана система линейных уравнений:
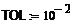 |
Для решения системы уравнений выполним следующие действия:
· Зададим точность вычислений:
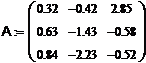
· Составим матрицу системы. Для этого запишем в матрицу все коэффициенты, стоящие перед неизвестными. Тогда матрица системы будет выглядеть следующим образом:
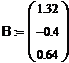
· Составим вектор правых частей. Для этого запишем в вектор правые части всех уравнений сверху вниз:
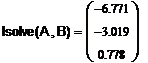
· После того как были проведены вышеперечисленные действия, применим функцию lsolve(Матрица системы, Вектор правых частей):
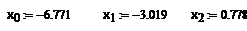
Значит
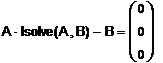
· Также необходимо проверить правильность решения. Для этого перенесем элементы правой части каждого уравнения в левую часть с противоположным знаком, следовательно, в правой части должны получится 0:
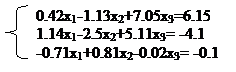
Дата: 2018-09-13, просмотров: 7676.