Для того, чтобы решить ОДУ высокого порядка с помощью функций Rkfixed(), Rkadapt(),Bulstoer(), следует сперва преобразовать ОДУ к системе ОДУ первого порядка.
ОДУ n- порядка сводится к системе n уравнений 1-го порядка.
Алгоритм приведения ОДУ высшего порядка к системе ОДУ первого порядка:
· Пусть дано уравнение второго порядка:
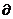
· Проведем некоторые преобразования:
Пусть у будет равна y0, у` = у1 .
Составим систему уравнений:
Ø Так как у = у0, у` - производная от у, а у` = у1, то у0` = y1. запишем последнее равенство в систему.
Ø Так как у` = у1, y`` - производная от у`, то у1` = y``. Рассмотрим выражение 
. Перепишем его в ином виде 
. Получилось ОДУ первого порядка. Запишем производную от у1 и остаток выражения по разные стороны от знака равенства и внесем результат в систему. В конечном итоге получена система ОДУ первого порядка:
Данная система ОДУ решается при помощи встроенных функций Rkfixed(), Rkadapt(),Bulstoer(). Пример решения системы ОДУ первого порядка описан в параграфе 7.2.2.1.
7.2.3. Использование дополнительных функций
Функция rkfixed() не всегда является быстродействующей, хотя приводит к искомому результату. Однако имеются случаи, когда результат можно получить точнее. Если известно, что решение дифференциального уравнения является “жесткой” функцией (решение неустойчивое, с разрывами, асимптотами), то следует использовать функции Stiffb(), Stiffr().
Форматы функций Stiffb() (метод Булирша – Стейна для решения жестких систем ОДУ) и Stiffr() (метод Розенборка для решения жестких систем ОДУ) следующие:
Stiffb(y,x1,x2,npoints,D,J)
Stiffr(y,x1,x2,npoints,D,J),
где y – вектор начальных значений в начальной точке;
x1 – начальная точка расчета;
x2 – конечная точка расчета;
npoints – число шагов численного метода;
D – векторная функция задающая систему ОДУ (пример сохдания этой функции описан в параграфе 7.2.2.1.)
J(x,y) – функция, возвращающая матрицу n 
(n+1). Первый столбец содержит производные 
D/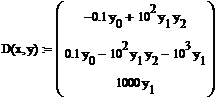 
x, остальные строки и столбцы представляют собой матрицу Якоби ( 
D/ y 
)
Рассмотрим работу алгоритма на примере. Дана система:
· Составим вектор начальных условий:
· Проведем некоторые преобразования:
Пусть у будет равна y0. Тогда у` = у1, у`` = у2 и так далее.
· Составим систему уравнений:
Ø Так как у = у0, у` - производная от у, а у` = у1, то у0` = y1. запишем последнее равенство в систему.
Ø Так как у` = у1, y`` - производная от у`, то у1` = y``. Рассмотрим выражение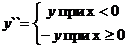 
. Перепишем его в ином виде . Получилось ОДУ первого порядка. Запишем производную от у1 и остаток выражения по разные стороны от знака равенства и внесем результат в систему. такие же действия проведем со второй и третьей производными. В конечном итоге получена система ОДУ первого порядка. Запишем данную систему в матрицу D
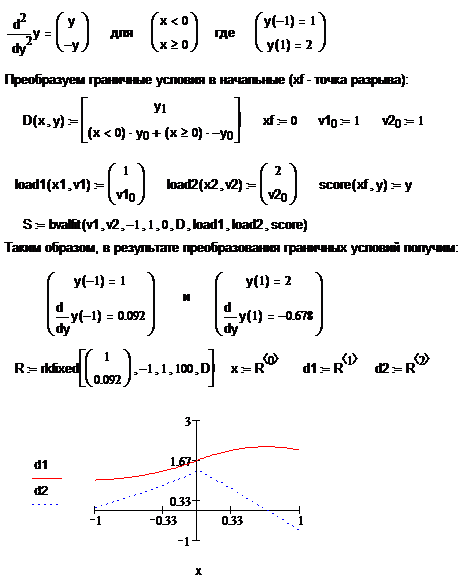
· Составим матрицу Якоби:
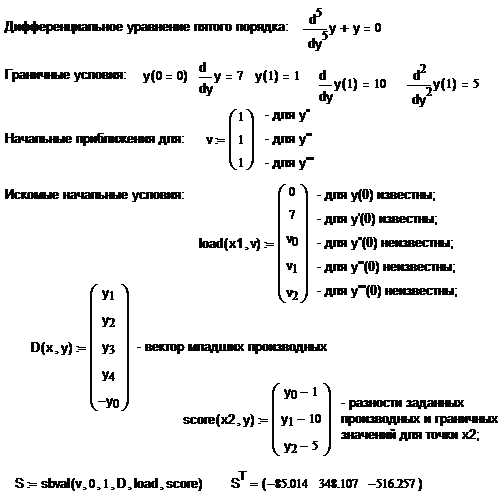
· Применим функцию Stiffb():
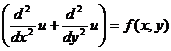
· Результатом вычисления (как и функций класса rkfixed()) будет матрица, содержащая в первом столбце значение х, во втором – значения у при определенных значениях х, далее – значения производных функции (по возрастанию степени).
· Решение системы можно представить графически. Для этого на оси 0х отложить значения х (первый столбец матрицы), а по оси 0у отложить значения функций и производных функции в точках х:
При решении краевых задач с граничными условиями часто выполняют преобразования граничных условий к начальным. Такое преобразование дает возможность функции группы rkfixed() использовать для решения некоторых дифференциальных уравнений с частными производными (ДУЧП).
Функция bvalfit() выполняет преобразования граничных условий, заданных на интервале поиска решения и возвращает вектор начальных условий в неизвестной точке х1.
Она имеет формат:
Bvalfit(v1,v2,x1,x2,xf,D,load1,load2,score)
Где: v1 – вектор, содержащий неполные граничные условия для x1;
v2 – вектор, содержащий неполные условия для x2;
x1 и x2- начальные и конечные точки интервала, на котором решается ДУЧП;
xf- точка на интервале (х1,х2), в которой искомая функция при поиске решения от х1 и х2 имеет одинаковые значения;
D- n-мерный вектор младших производных:
load1 – искомый вектор граничных значений для точки х1;
load2 – искомый вектор граничных значений для точки х2;
score – n-мерный вектор значений функции и ее производных в точке xf. Если score(xf,y)=y, то все значения производных справа и слева совпадают.
Рассмотрим использование функции на примере.
Решить уравнение:
При заданных начальных условиях:
Пример 7.2. Решить уравнение:
Функция sbval() вычисляет недостающие начальные условия в точке х1 и тем самым преобразует краевую задачу в задачу Коши. Она имеет формат
sbval(v,x1,x1,D,load,score),
где: v – вектор для начальных значений младших производных (задаются как начальные приближения для искомых производных в точке х1);
x1, x2 – начальное и конечное значение интервала поиска решения;
D – n-мерный вектор младших производных;
load – вектор начальных условий для точки х;
score – разность производных и их граничных значений в точке х2.
Пример 7.3. Решить дифференциальное уравнение с граничными значениями:
После нахождения искомых начальных условий можно задачу решать с помощью функций группы rkfixed().
Для решения дифференциального уравнения в частных производных типа уравнения Пуассона
- 
используется функция relax(a,b,c,d,e,f,u,rjac), возвращающая квадратную матрицу в которой:
- расположение элементов матрицы соответствует расположению сетки внутри квадратной области;
- значение элемента матрицы аппроксимирует значение искомого решения.
Для обеспечения сходимости решения используется релакционный метод. Эту функцию целесообразно использовать, если граничные значения на концах области отличны от нуля. Если все граничные значения на концах области равны нулю, то необходимо использовать функцию multigrid(). Пример использования функции relax():
Дата: 2018-09-13, просмотров: 4915.
