Составим алгоритм использования данных функций:

Дана система ОДУ:

Примечание: если исходная система дана в ином виде, следует привести её к виду, указанному вначале главы 7.2.2.

· Составим вектор D. В векторе D определяется правая часть системы ОДУ. Здесь следует сказать несколько слов о форме записи вектора D . Первый параметр вектора D – неизвестный аргумент, относительно которого задана функция Y. Второй параметр – вектор Y (приглядитесь, элементами вектора D являются элементы вектора у. Это важно: вектор у составлен путем замены y₀(t)=y(t), y₁(t)=y^`(t), y₂(t)=y``(t)….).

· Составим вектор начальных приближений (имеет ту же размерность, что и D(t,y)):

Заметьте, записано не у₀, а у0 (т.е. у0 не является элементом вектора у).

· Запишем интервал. Интервал задается вторым и третьим параметрами встроенной функции:

· Зададим количество шагов (четвертый параметр функции):

· Используем функцию:

Замечание: описываемые функции возвращают массив значений в котором:

Ø Первый столбец – вектор неизвестных (узлы сетки);

Ø Второй столбец – вектор функции (значения функции в узлах сетки);

Ø Третий и последующие столбцы – вектора производных функции.

· По данным данного массива можно построить графики функции и ее производных:

Используем функцию Bulstoer() :

· Строим график:

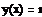
Используем функцию Rkadapt() :

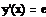
· Строим график:

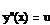
Примечание: следует строго соблюдать регистр написания функции.

Решение ДУ высших порядков

В MathCad 2001 можно решать ДУ высших порядков как с помощью вычислительного блока Given-Odesolve(), так и путем сведения их к системам уравнений первого порядка. Рассмотрим эти два способа решения ДУ высших порядков подробнее.

Использование функции Given-Odesolve()

Формат записи внутри вычислительного блока:

· ОДУ должно быть записано в стандартной форме, т.е. относительно старшей производной;

· Начальные условия должны иметь простую форму:

……

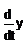
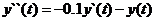
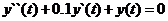
· Все равенства записываются через жирное равно (Ctrl + =);

· Знак ' ставится с помощью сочетания клавиш (Shift + F7) или клавишей `. вместо знака ` можно использовать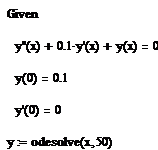

Рассмотрим использование вычислительного блока на примере решения ОДУ второго порядка. Дано уравнение:

· Представим данное уравнение в стандартном виде:

· Даны начальные условия:

y (0) = 0.1

y `(0) = 0

· Запишем данные в вычислительный блок:

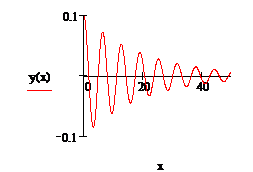
· Решением ОДУ является функция. Покажем данную функцию на графике: