При проведении научно-технических расчетов часто используются таблицы вида y(x), полученные экспериментальным путем.

 В этих таблицах каждому значению х соответствует определенное значение функции у(x).

 Ставится задача построить функцию, проходящую через точки (х, у) на определенном отрезке (задача интерполяции) и за его пределами (задача экстраполяции), спецификации задачи может отвечать различным требованиям:

· Функция должна проходить через точки (x_i, y_i), то есть f(x_i)=y_i . В этом случае говорят о интерполяции данных, заданных таблицей, функцией f(x) во внутренних точках между узлами сетки, или экстраполяции (функции предсказания) за пределами интервала содержащего все x_i.

· Функция должна некоторым образом приближать y(x_i) необязательно проходя через узлы сетки. В данном случае речь идет о регрессии.

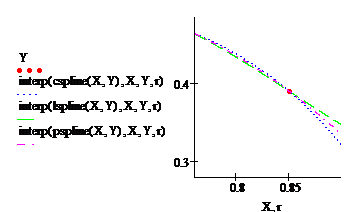
Для построения интерполяции или экстраполяции MathCad имеет ряд встроенных функций, позволяющих соединить узлы сетки кривой какой – либо степени гладкости.

Линейная интерполяция

При выполнении линейной интерполяции MathCAD соединяет смежные точки табличной функции прямыми линиями, представляя функцию в виде ломаной линии. Тогда по такой функции можно определить любые промежуточные значения в заданном интервале. Эти вычисления выполняются встроенной функцией linterp(). Она имеет формат

linterp(vx,vy,t)

где vx – вектор, состоящий из значений х, заданных в таблице исходных данных (замечание: элементы вектора х должны располагаться в порядке возрастания)

   vy – вектор состоящий из значений у заданных в таблице исходных данных (замечание: определенному);

t – аргумент, при котором нужно найти промежуточное значение y. Вектор vx должен содержать вещественные значения, расположенные в порядке возрастания.

При небольшом числе узловых точек (менее 10) линейная интерполяция оказывается довольно грубой. При ней даже первая производная функции аппроксимации испытывает резкие скачки в узловых точках. Для целей экстраполяции функция linterp() не предназначена и за пределами области определения может вести себя непредсказуемо.

Построим график функции используя линейную интерполяцию. Алгоритм построения графика состоит из нескольких этапов:

· Пусть дана таблица исходных данных:

·
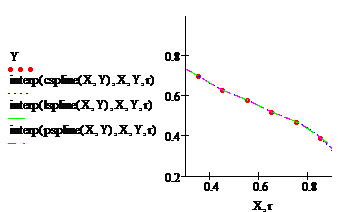
Определение вектора неизвестных (берется из таблицы данных. В нашем случае Х можно записать в виде ранжированной переменной, потому что нетрудно увидеть зависимость между последующим и предыдущим значением каждого из Х):

· Определение вектора Y (берется из таблицы данных):

· Встроенная функция linterp() вычисляет значение в конкретной точке (последний параметр функции), но так как нам необходимо построить график, то мы заменим параметр t неизвестной (например, r), не имеющей дискретного значения, и подставим эту переменную в нижний местозаполнитель декартовой системы координат (плоский график). построим график, отформатируем его по своему усмотрению:

A(r):= linterp(X,Y,r)

Чтобы вычислить значение графика в какой – либо точке, необходимо поставить вместо r число. Замечание: данные действия необходимо производить вне графической зоны.

Пример: Вычислим значение функции, построенной с помощью линейной интерполяции в точке 2.1: