Добавить исследование систем однородных уравнений

Исследовать неоднородную СЛАУ – это значит установить является ли она совместной и если является, то найти выражение для общего решения системы. Для того чтобы неоднородная СЛАУ была совместна – необходимо и достаточно, чтобы ранг расширенной матрицы совпадал с рангом матрицы.

Порядок выполнения работы .

1.Ввести матрицу системы и вектора правых частей.

2.Получить расширенную матрицу системы (augment(A,b1))

3.Вычислить ранг основной и ранг расширенной матрицы.

4.Сформулировать вывод о существовании решения (система совместна?)

5.Привести расширенную матрицу совм. системы к ступенчатому виду (rref(Ar))

6.Определить базисные и свободные переменные.

7.Записать эквивалентную систему и разрешить ее относительно базисных переменных.

8.Записать общее решение системы.

9.Найти частное решение системы.

Исследуем СНЛУ.

· Дана СНЛУ:

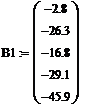· Составим матрицу системы:

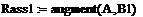
· Запишем вектор правых частей:

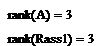
· Получим расширенную матрицу используя, оператор augment(матрицы, подлежащие слиянию). Дадим новой матрице имя Rass1:

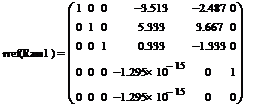
· Вычислим ранг основной и расширенной матрицы и сравним их. Если ранги совпадают, то система совместна. Для нахождения ранга матрицы используем оператор rank(матрица):

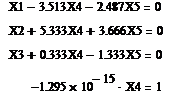
Ранг расширенной и исходной матриц совпадают, следовательно, система совместна.

· Приводим расширенную матрицу к ступенчатому виду (путем простых алгебраических преобразований ниже и выше главной диагонали получаем 0). Для приведения матрицы к ступенчатому виду используем оператор rref(матрица):

Матрица приведена к ступенчатому виду. Элементы (4,4) и (5,4) очень близки к нулю, следовательно, примем их значения = 0.

· Определим базисные и свободные переменные.

Базисные переменные: x1, x2, x3.

Свободные переменные: х4, х5.

· Подставим в ступенчатую матрицу неизвестные (элементы матрицы являются коэффициентами при неизвестных, а последний столбец матрицы – вектор правых частей):

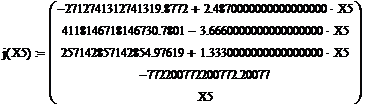
· Решим полученную систему уравнений с помощью вычислительного блока. Заглядывая наперед можно сказать, что неизвестная х5 не получит численного значения, поэтому после оператора Find (список неизвестных) необходимо поставить оператор символьного вывода:

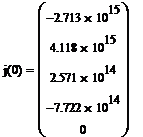
· Запишем общее решение системы:

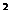
Каждой строке в векторе j(х5) соответствует одна переменная (от х1 до х5, снизу вверх соответственно).

· Найдем частное решение системы. Частное решение будет получено при конкретном (частном) значении х5 (например: х5 = 0):

Смысл вычислений, проведенных в последнем пункте, состоит в вычислении значений переменных х1, х2, х3, х4 при заданном значении х5 (в данном случае х5 = 0).