Метод Крамера состоит из следующих действий:

Составим матрицу системы.

· Составим вектор правых частей.

· Проверяем неравенство детерминанта матрицы системы нулю (необходимо, потому что далее производится деление на детерминант матрицы системы [деление на ноль запрещено]. Если детерминант матрицы системы равен нулю, то можно сделать вывод, что система имеет множество решений). Если детерминант матрицы не равен 0, то выполняем следующие действия:

· Для вычисления первой, второй и третьей неизвестной подставляем вектор правых частей в первую, вторую или третью колонку матрицы системы соответственно.

Ø Вычисляем детерминант полученной матрицы.

Ø Делим полученный детерминант на детерминант матрицы системы.

Ø Записываем, найденную неизвестную, в вектор.

Посмотрим на примере как данную последовательность действий реализовать с помощью MathCad 2001:

· Дана система:

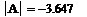· Найдем матрицу системы:

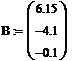
· Проверим неравенство детерминанта матрицы системы 0:

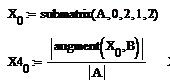
Детерминант матрицы системы не равен 0, следовательно, система имеет единственное решение.

· Преобразуем матрицу системы, подставляя вектор правых частей вместо первого, второго и третьего столбца (используем функции submatrix(Матрица, начальная строка, конечная строка, начальный столбец, конечный столбец) и Augment(Матрица, Матрицы, ..)). Затем делим детерминант, полученной матрицы, на матрицу системы. Заносим результат в вектор:

- Для первой неизвестной:

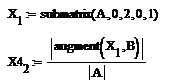
- Для второй неизвестной:

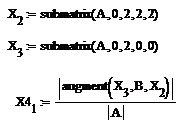
- Для третьей неизвестной:

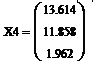
· Выводим вектор неизвестных:

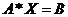
· Сделаем проверку:

Получился практически нулевой столбец, что говорит о правильно проведенных вычислениях.

Использование матричного метода.

Сущность матричного метода.

Система в матричном виде выглядит как . В результате цепочки преобразований, получим решение системы (замечание: записывается , а не . Потому что при умножении матриц должно выполняться условие: число строк равно числу столбцов и никак иначе):

Назовем результат проведенных действий формулой метода и посмотрим на примере как данную последовательность действий реализовать с помощью MathCad 2001:

· Дана система:

· Составим матрицу системы:

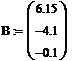
· Составим вектор правых частей:

· Применим формулу матричного метода:

· Выведем вектор неизвестных:

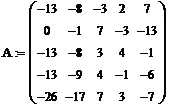
· Сделаем проверку:

Получился практически нулевой столбец, что говорит о правильно проведенных вычислениях.