В интегрированной среде MathCAD имеются средства для отыскания корней уравнения с одной и многими переменными. Для этой цели используются встроенные функции. Рассмотрим некоторые из них подробней.
7.1.1. Функция root (f(z),z,a,b)
Функция root ( f ( z ), z , a , b ) возвращает скаляр z, при котором выражение или скалярная функция f(z) обращается в ноль на интервале [a,b]. Варьируя начальное приближение z, MathCAD будет пытаться найти такое значение функции, при котором функция f(z)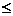 
TOL, где TOL – встроенная переменная, указывающая заданную степень точности (по умолчанию TOL=10 
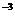). Если интервал [a,b] не указан, то перед использованием функции root() используют метод секущей. Начальное приближение, заданное пользователем, становится первым приближением при поиске корня. Если процесс сходится, то итерация заканчивается, когда значение f(x) становится меньше TOL. Если процесс расходится и MathCAD не может найти корень, итерация прекращается и выдается сообщение – “Cannot evaluate this accurately at one or more of the values you specified” – «Не могу это вычислить точно по одной или более переменным, которые вы указали».
Некоторые рекомендации использования функций root():
- для изменения точности поиска корней, можно изменить значение встроенной переменной TOL. Если уменьшить TOL, то число итераций функции root() будет увеличиваться, но решение будет точнее. Если увеличить TOL, то число итераций уменьшается и корень будет найден грубее. Изменить TOL можно непосредственно в рабочем документе (например, TOL:=0.0001) или через меню Math/Options/Built – in Variables tab;
- для поиска нескольких корней можно менять интервал [a,b] или начальные приближения. В этом случае целесообразно воспользоваться графиком функции f(x). Точки пересечения кривой f(x) с осью х графически определяют значение и число корней;
- если функция root() имеет малый наклон около искомого корня, можно или уменьшить TOL, или заменить функцию f(x)=0 на функцию g(x)=0, где g(x)= f(x)/f’(x);
- для выражения f(x) с известным корнем a, т.е. f(a)=0, нахождение дополнительных корней эквивалентно поиску корней уравнения h(x)=0, где h(x)=f(x)/(x-a). Этот прием полезен для отыскания корней, расположенных близко друг к другу.
Рассмотрим примеры использования функции root ()
Построим алгоритм нахождения корней уравнения с помощью встроенной функции root().
· Пусть дан полином 3-й степени. Запишем его в виде:
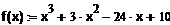
· Зададим точность.
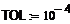
· построим график функции f(x). Для этого выполним следующие действия:
Ø зададим ранжированную переменную х (ранжир выбирается произвольно):
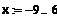
Ø Создадим двумерный график (Shift + 2).
Ø Введем значения в местозаполнители следующим образом:
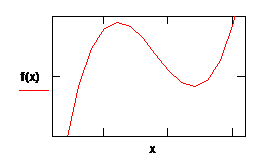
Ø Отформатируем график:
Ø График построен
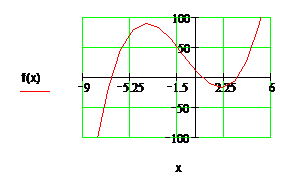
· Теперь необходимо выбрать отрезок, на концах которого функция принимает значения разных знаков (т.е. отрезки, на которых функция единожды пересекает ось абсцисс). Например, отрезок [-9; -5.25] или [-1.5; 2.25].
· После того как были проведены все вышеперечисленные действия, можно применить функцию root(полином, переменная, начало отрезка, конец отрезка).
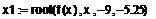
· Для просмотра результата необходимо ввести x1= и нажать клавишу Enter. В результате получим равенство:
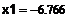
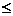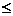Функция root () может быть использована для поиска корней двух уравнений от одной переменной. Например, пусть даны два уравнения y1=f(x) и y2=g(a,x) и требуется найти их действительные корни, т.е. точки пересечения. Составим новую функцию S(a,x)= root(f(x)-g(a,x),x) и найдем корни. Составим дискретный аргумент -1 x 1 с шагом 0.01. Построим графики функций f(x) и g(x,a) для различных a.
· Для этого запишем уравнения в виде:
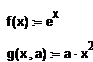
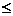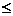· Составим дискретный аргумент -1 x 1 с шагом 0.01:
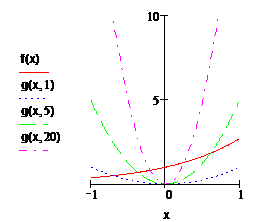
· Построим график функций причем коэффициент а в функции g(x,a) примет значения 1, 5, 20. Чтобы построить на одном графике несколько функций, необходимо записать эти функции в местозаполнитель слева через запятую:
Теперь вычислим аналитически корни системы, имея ввиду, что коэффициент а изменяется от 1 до 20 с шагом 1. Для того чтобы решить систему двух уравнений необходимо свести систему к одной функций. Известно, что решением системы уравнений являются точки пересечения этих уравнений на графике. Следовательно:
f(x)=g(a,x)
тогда, решением системы также будет выражение f(x)-g(a,x)=0 (перенесли функцию g(a,x) в левую часть.). Далее выполним следующие действия:
· зададим ранжированную переменную а:
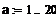
· зададим начальное приближение. В качестве начального приближения возьмем начало отрезка [-1; 1]. Т.е.
х0 = -1
· построим итерационный процесс по формуле:
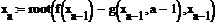
Данный процесс на каждом шаге рассчитывает каждый последующий корень на основе предыдущего. Таким образом, мы найдем все 20 корней системы уравнений, каждый корень системы соответствует одному значению коэффициента а. Значит решение системы можно записать в виде таблицы:
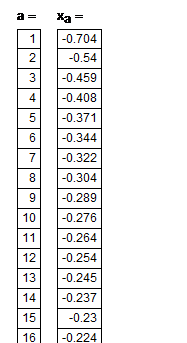
Функция Polyroots()
Если f(x) представляет собой полином и его коэффициенты, начиная со свободного члена, можно представить в виде вектора v, то для поиска одновременно всех корней полинома можно использовать функцию polyroots(v).
Построим алгоритм нахождения корней полинома с помощью встроенной функции polyroots(). Функция polyroots() находит все возможные корни уравнения и выводит их пользователю в виде вектора.
Рассмотрим пример использования функции polyroots ().
· Пусть дан полином 3-й степени. Запишем его в виде:
· Зададим точность:
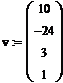
· Запишем коэффициенты полинома в вектор v, начиная с коэффициента, стоящего у неизвестного низшей степени, т.е. x0. Тогда вектор v примет вид:
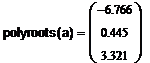
· После того, как были проведены все вышеперечисленные действия можно применить встроенную функцию polyroots(вектор коэффициентов).
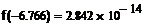
· Чтобы сделать проверку, необходимо в исходную функцию поочередно подставить корни уравнения. Т.е.:
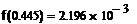
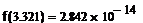
Если вычисления проведены правильно, то в результате проверки значение функции в корнях уравнения должны быть равны 0 или числам близким к 0 (все зависит от заданной точности).
Дата: 2018-09-13, просмотров: 8831.
