Функциональный ряд вида
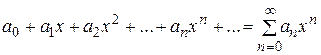 (2.5)
(2.5)
называется степенным.
Если ряд (2.5) расходится хотя бы в одной точке, то существует такое число R,
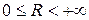 , что
, что
1) для 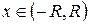 ряд (2.5) сходится;
ряд (2.5) сходится;
2) для 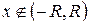 ряд (2.5) расходится.
ряд (2.5) расходится.
Это число R называется радиусом сходимости степенного ряда, а интервал 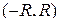 - интервалом сходимости. Радиус сходимости ряда (2.5) удобно находить:
- интервалом сходимости. Радиус сходимости ряда (2.5) удобно находить:
1) по формулам 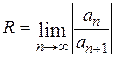 или
или 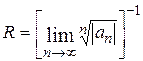 , если пределы существуют;
, если пределы существуют;
2) При помощи признаков Даламбера и Коши.
Полезно запомнить следующие свойства степенных рядов:
- на любом отрезке, целиком принадлежащем интервалу сходимости, степенной ряд сходится абсолютно и равномерно;
- на любом отрезке, целиком принадлежащем интервалу сходимости, степенной ряд можно почленно интегрировать любое число раз;
- в любой точке интервала сходимости степенной ряд можно почленно дифференцировать любое число раз.
Напомним, что на интервале 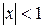
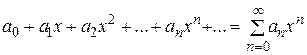
(сумма геометрической прогрессии).
Пример 2.7. Найти сумму ряда
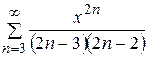
Легко убедиться, что интервал сходимости ряда - 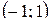 . На этом интервале
. На этом интервале 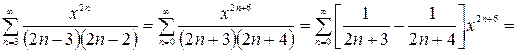
= 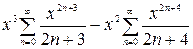 (2.6)
(2.6)
Ряды, стоящие в правой части (2.6), можно получить интегрированием рядов
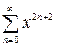 ,
, 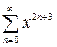 ; при этом
; при этом
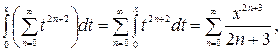

Заметим, что 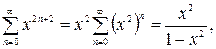
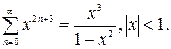 Значит,
Значит, 
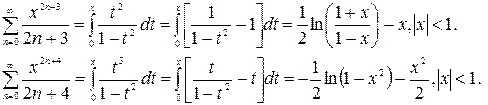 (2.7)
(2.7)
Поэтому, с учетом (2.6), (2.7),имеем
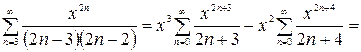
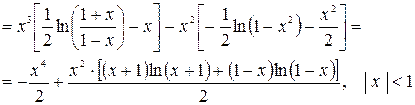
Пример 2.8. Найти сумму ряда
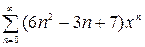
При последовательном дифференцирование ряда 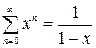 на интервале сходимости |x|<1 получим:
на интервале сходимости |x|<1 получим:

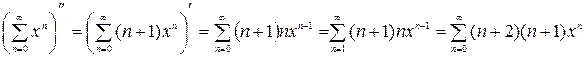 .
.
Значит, 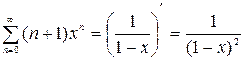 ,
,
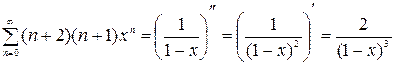 .
.
Представим многочлен 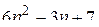 в виде:
в виде:  ,
,
где A, B, С – неопределённые коэффициенты, которые найдём, решив систему:
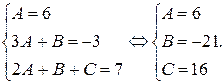
Поэтому
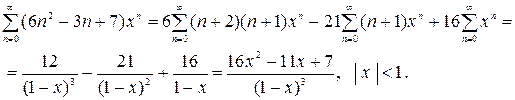
Разложение функций в ряды.
Если функция 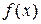 определена вместе со своими производными в некоторой окрестности точки
определена вместе со своими производными в некоторой окрестности точки 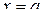 , то она разложима в ряд Тейлора:
, то она разложима в ряд Тейлора:
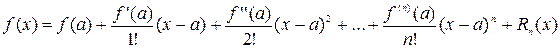
 (2.8)
(2.8)
при условии, что остаток ряда
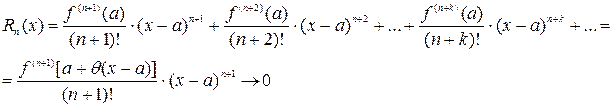
(стремится к нулю) при 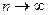 . Здесь
. Здесь 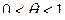 , а остаток записан в форме Лагранжа.
, а остаток записан в форме Лагранжа.
Разложение (2.8), в частности, имеет место в промежутке 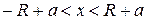 , если функция
, если функция 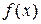 имеет в нём ограниченные производные всех порядков, то есть если
имеет в нём ограниченные производные всех порядков, то есть если 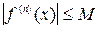 при всех
при всех 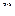 .
.
При а = 0 ряд Тейлора имеет вид:
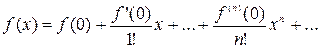


и называется рядом Маклорена.
Основными табличными разложениями являются:
1) 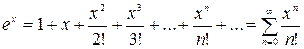 ,
, 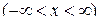 ,
,
2) 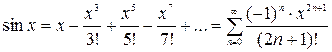
 ,
, 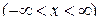 ,
,
3) 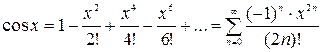 ,
, 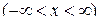 ,
,
4) 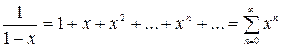 ,
, 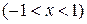 ,
,
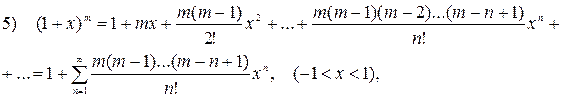
6) 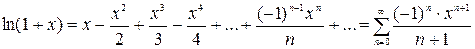 ,
, 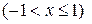 ,
,
7) 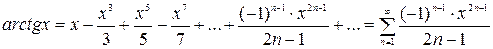 ,
,
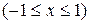 .
.
Используя эти разложения, можно довольно просто находить разложения многих других функций.
Пример 2.9. Разложить в функцию 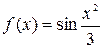 в ряд Маклорена.
в ряд Маклорена.
Решение. Полагаем 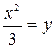 . Тогда
. Тогда
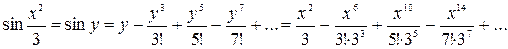
Разложение имеет место при всех х.
Иногда разложение функции в ряд получается суммированием табличных рядов.
Пример 2.10. Разложить в ряд функцию 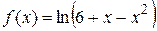
Решение:
Так как 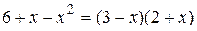 , то
, то 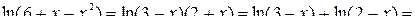
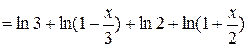 , при
, при 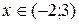
Учитывая, что 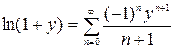 ,
, 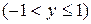 , получим:
, получим:
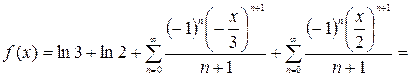
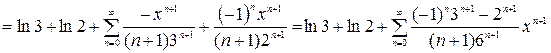 .
.
Разложение имеет место при
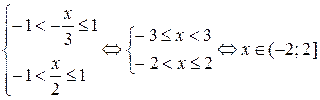
Для разложения функции в ряд Тейлора в окрестности точки а (то есть, по степеням (х-а)), находят коэффициенты непосредственно, т.е. вычисляют значения производных, либо преобразуют функцию.
Пример 2.11. Разложить в ряд функцию 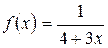 по степеням (х+2) и указать интервал сходимости полученного разложения.
по степеням (х+2) и указать интервал сходимости полученного разложения.
Решение.
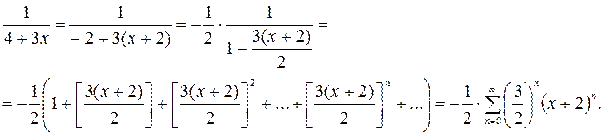
Полученное разложение верно для всех х , удовлетворяющих неравенству:
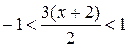 или
или 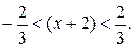
Вычитая из каждой части неравенства по 2 , получаем:
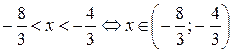
область сходимости ряда к своей функции. 
Задача 1. Вычислить неопределенные интегралы.
1.1. 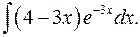 1.2.
1.2. 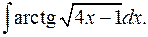
1.3. 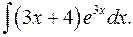 1.4.
1.4. 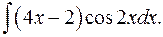
1.5. 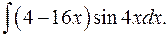 1.6.
1.6. 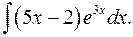
1.7. 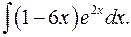 1.8.
1.8. 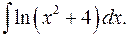
1.9. 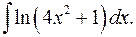 1.10.
1.10. 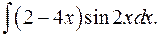
1.11. 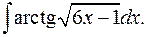 1.12.
1.12. 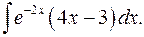
1.13. 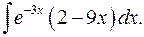 1.14.
1.14. 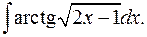
1.15. 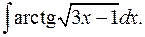 1.16.
1.16. 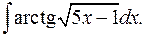
1.17. 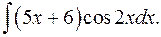 1.18.
1.18. 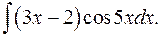
1.19. 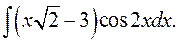 1.20.
1.20. 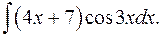
1.21. 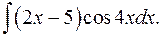 1.22.
1.22. 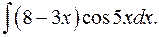
1.23. 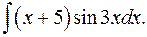 1.24.
1.24. 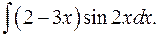
1.25. 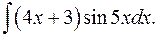 1.26.
1.26. 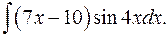
1.27. 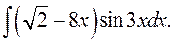 1.28.
1.28. 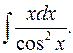
1.29. 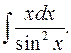 1.30.
1.30. 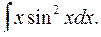
1.31. 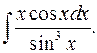
Задача 2. Найти неопределенные интегралы.
2.1. 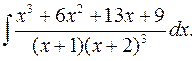 2.2.
2.2. 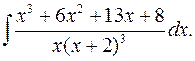
2.3. 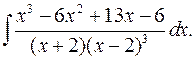 2.4.
2.4. 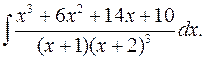
2.5. 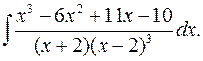 2.6.
2.6. 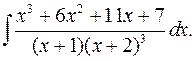
2.7. 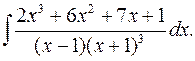 2.8.
2.8. 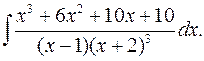
2.9. 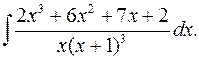 2.10.
2.10. 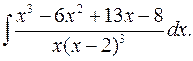
2.11. 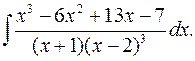 2.12.
2.12. 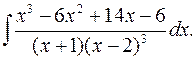
2.13. 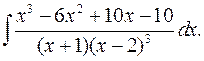 2.14.
2.14. 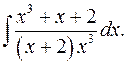
2.15. 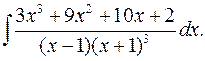 2.16.
2.16. 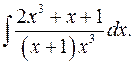
2.17. 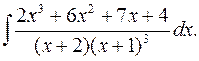 2.18.
2.18. 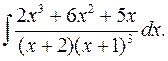
2.19. 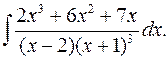 2.20.
2.20. 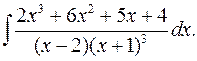
2.21. 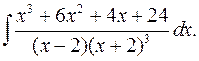 2.22.
2.22. 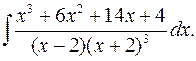
2.23. 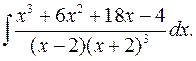 2.24.
2.24. 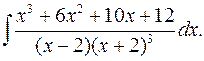
2.25. 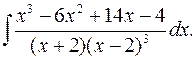 2.26.
2.26. 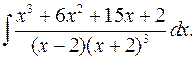
2.27. 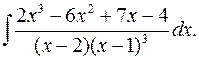 2.28.
2.28. 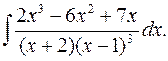
2.29.  2.30.
2.30. 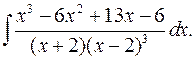
2.31. 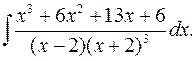
Задача 3. Вычислить площади фигур, ограниченных графиками функций.
3.1. 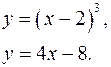 3.2.
3.2. 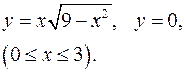
3.3. 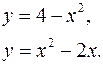 3.4.
3.4. 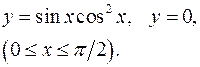
3.5. 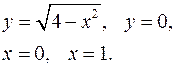 3.6.
3.6. 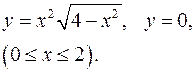
3.7. 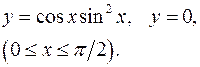 3.8.
3.8. 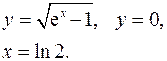
3.9. 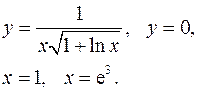 3.10.
3.10. 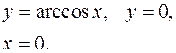
3.11. 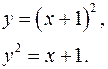 3.12.
3.12. 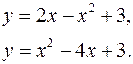
3.13. 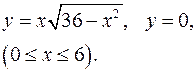 3.14.
3.14. 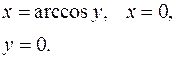
3.15. 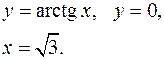 3.16.
3.16. 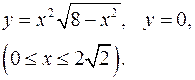
3.17. 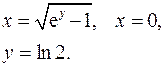 3.18.
3.18. 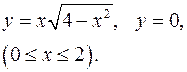
3.19. 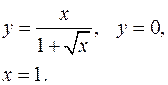 3.20.
3.20. 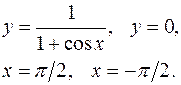
3.21. 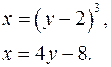 3.22.
3.22. 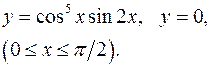
3.23. 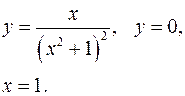 3.24.
3.24. 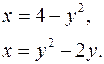
3.25. 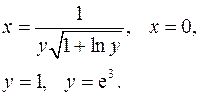 3.26.
3.26. 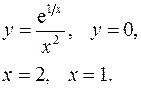
3.27. 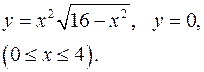 3.28.
3.28. 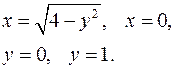
3.29. 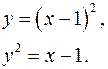 3.30.
3.30. 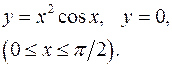
3.31. 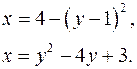
Задача 4. Найти общий интеграл дифференциального уравнения. (Ответ представить в виде 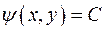 .)
.)
4.1. 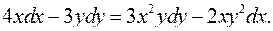 4.2.
4.2. 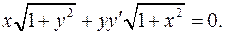
4.3. 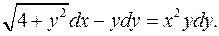 4.4.
4.4. 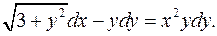
4.5. 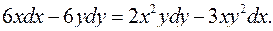 4.6.
4.6. 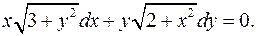
4.7. 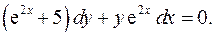 4.8.
4.8. 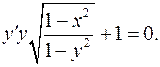
4.9. 
4.10. 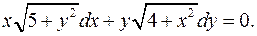
4.11. 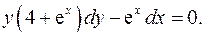 4.12.
4.12. 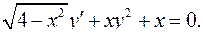
4.13. 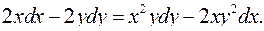
4.14. 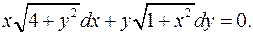
4.15. 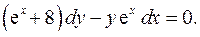 4.16.
4.16. 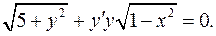
4.17. 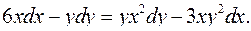 4.18.
4.18. 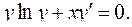
4.19. 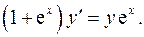 4.20.
4.20. 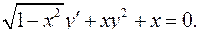
4.21. 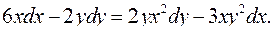 4.22.
4.22. 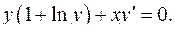
4.23. 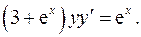 4.24.
4.24. 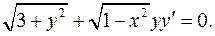
4.25. 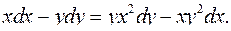 4.26.
4.26. 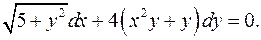
4.27. 
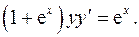 4.28.
4.28. 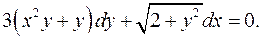
4.29. 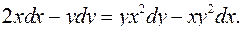 4.30.
4.30. 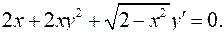
4.31. 
Задача 5. Найти решение задачи Коши.
5.1. 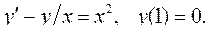 5.2.
5.2. 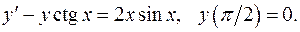
5.3. 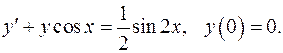
5.4. 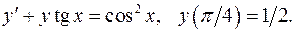
5.5. 
5.6. 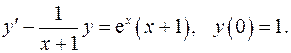
5.7. 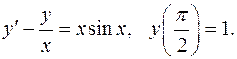 5.8.
5.8. 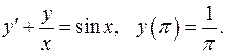
5.9. 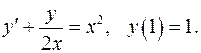 5.10.
5.10. 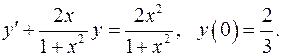
5.11. 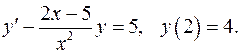 5.12.
5.12. 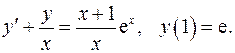
5.13. 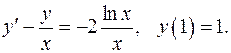 5.14.
5.14. 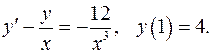
5.15. 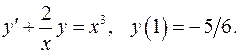 5.16.
5.16. 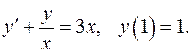
5.17. 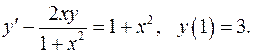 5.18.
5.18. 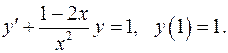
5.19. 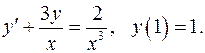 5.20.
5.20. 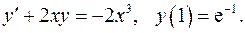
5.21. 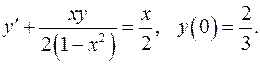 5.22.
5.22. 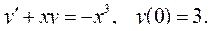
5.23. 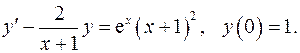
5.24. 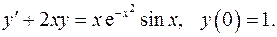
5.25. 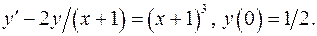
5.26. 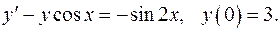
5.27. 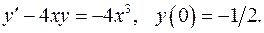 5.28.
5.28. 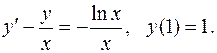
5.29. 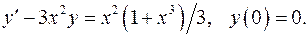
5.30. 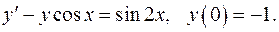
5.31. 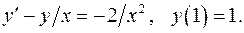
Задача 6. Найти общее решение дифференциального уравнения.
6.1. 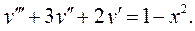 6.2.
6.2. 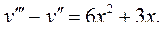
6.3. 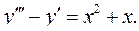 6.4.
6.4. 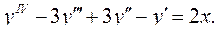
6.5. 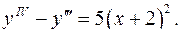 6.6.
6.6. 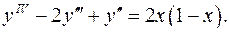
6.7. 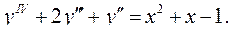 6.8.
6.8. 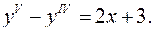
6.9. 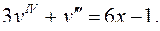 6.10.
6.10. 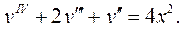
6.11. 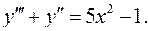 6.12.
6.12. 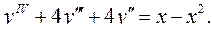
6.13. 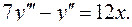 6.14.
6.14. 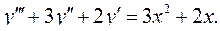
6.15. 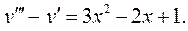 6.16.
6.16. 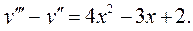
6.17. 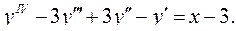 6.18.
6.18. 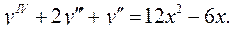
6.19. 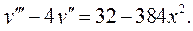 6.20.
6.20. 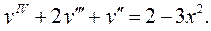
6.21. 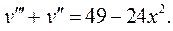 6.22.
6.22. 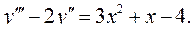
6.23. 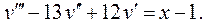 6.24.
6.24. 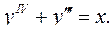
6.25. 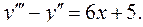 6.26.
6.26. 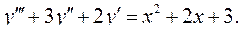
6.27. 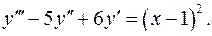 6.28.
6.28. 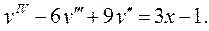
6.29. 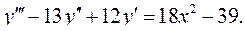 6.30.
6.30. 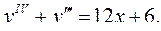
6.31. 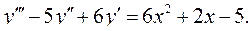
Задача 7. Найти сумму ряда.
7.1. 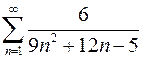 . 7.2.
. 7.2. 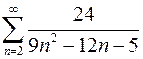 .
.
7.3. 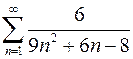 . 7.4.
. 7.4. 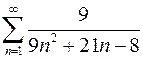 .
.
7.5. 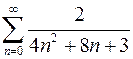 . 7.6.
. 7.6. 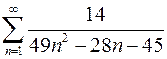 .
.
7.7. 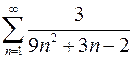 . 7.8.
. 7.8. 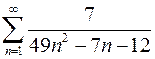 .
.
7.9. 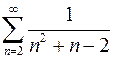 . 7.10.
. 7.10. 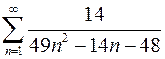 .
.
7.11. 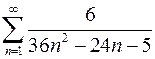 . 7.12
. 7.12 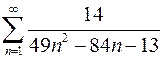 .
.
7.13 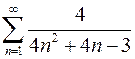 . 7.14
. 7.14 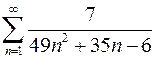 .
.
7.15. 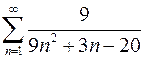 . 7.16
. 7.16 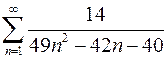 .
.
7.17. 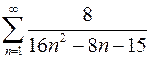 . 7.18.
. 7.18. 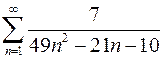 .
.
7.19. 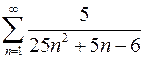 . 7.20.
. 7.20. 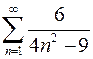 .
.
7.21. 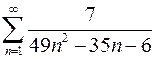 . 7.22.
. 7.22. 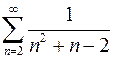 .
.
7.23. 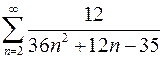 . 7.24.
. 7.24. 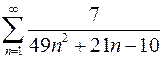 .
.
7.25 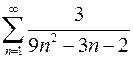 . 7.26.
. 7.26. 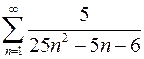 .
.
7.27.  . 7.28.
. 7.28. 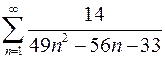 .
.
7.29. 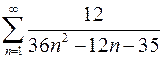 . 7.30.
. 7.30. 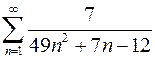 .
.
7.31. 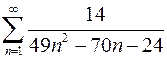 .
.
Задача 8. Исследовать на сходимость ряд.
8.1. 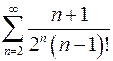 . 8.2.
. 8.2. 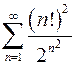 .
.
8.3. 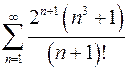 . 8.4.
. 8.4. 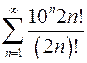 .
.
8.5. 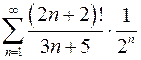 . 8.6.
. 8.6. 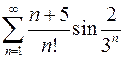 .
.
8.7. 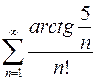 . 8.8.
. 8.8. 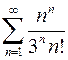 .
.
8.9. 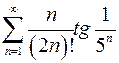 . 8.10.
. 8.10. 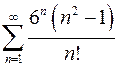 .
.
8.11. 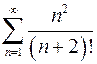 . 8.12.
. 8.12. 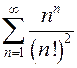 .
.
8.13. 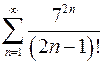 . 8.14.
. 8.14. 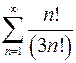 .
.
8.15. 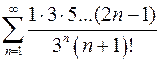 . 8.16.
. 8.16. 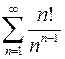 .
.
8.17. 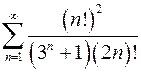 . 8.18.
. 8.18. 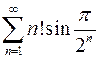 .
.
8.19. 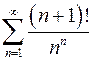 . 8.20.
. 8.20. 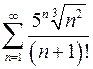 .
.
8.21. 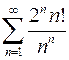 . 8.22.
. 8.22. 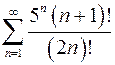 .
.
8.23. 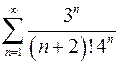 . 8.24.
. 8.24. 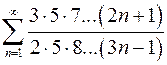 .
.
8.25. 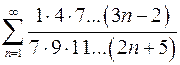 . 8.26.
. 8.26. 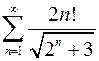 .
.
8.27. 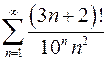 . 8.28.
. 8.28. 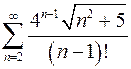 .
.
8.29. 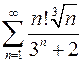 . 8.30.
. 8.30. 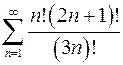 .
.
8.31. 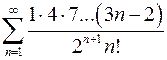 .
.
Задача 9. Найти область сходимости функционального ряда.
9.1. 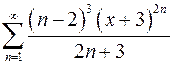 . 9.2.
. 9.2. 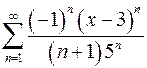 .
.
9.3. 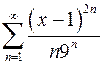 . 9.4.
. 9.4. 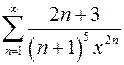 .
.
9.5. 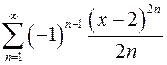 . 9.6.
. 9.6. 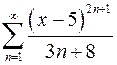 .
.
9.7. 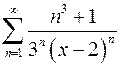 . 9.8.
. 9.8. 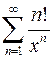 .
.
9.9. 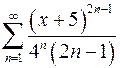 . 9.10.
. 9.10. 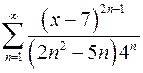 .
.
9.11. 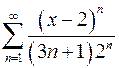 . 9.12.
. 9.12. 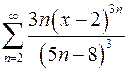 .
.
9.13. 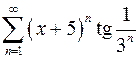 . 9.14.
. 9.14. 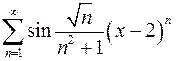 .
.
9.15. 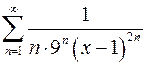 . 9.16.
. 9.16. 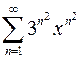 .
.
9.17. 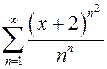 . 9.18.
. 9.18. 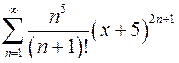 .
.
9.19. 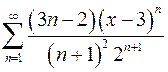 . 9.20.
. 9.20. 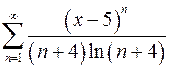 .
.
9.21. 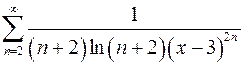 . 9.22.
. 9.22. 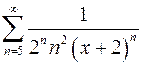 .
.
9.23. 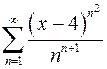 . 9.24.
. 9.24. 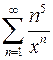 .
.
9.25. 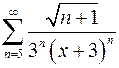 . 9.26.
. 9.26. 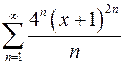 .
.
9.27. 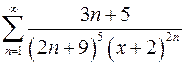 . 9.28.
. 9.28. 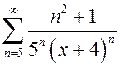 .
.
9.29. 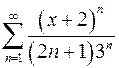 . 9.30.
. 9.30.  .
.
9.31. 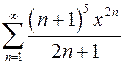 .
.
Задача 10. Разложить функцию в ряд Тейлора по степеням 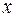 .
.
10.1. 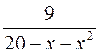 . 10.2.
. 10.2. 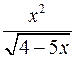 .
.
10.3. 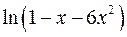 . 10.4.
. 10.4. 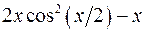 .
.
10.5. 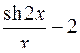 . 10.6.
. 10.6. 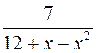 .
.
10.7. 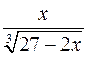 . 10.8.
. 10.8. 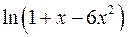 .
.
10.9. 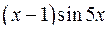 . 10.10.
. 10.10. 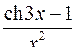 .
.
10.11. 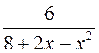 . 10.12.
. 10.12. 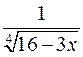 .
.
10.13. 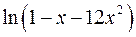 . 10.14.
. 10.14. 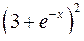 .
.
10.15. 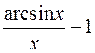 . 10.16.
. 10.16. 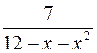 .
.
10.17.  . 10.18.
. 10.18. 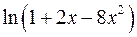 .
.
10.19. 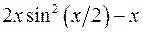 . 10.20.
. 10.20. 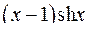 .
.
10.21. 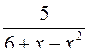 . 10.22.
. 10.22.  .
.
10.23. 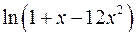 . 10.24.
. 10.24. 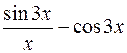 .
.
10.25. 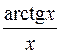 . 10.26.
. 10.26. 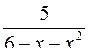 .
.
10.27. 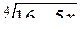 . 10.28.
. 10.28. 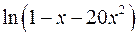 .
.
10.29. 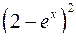 . 10.30.
. 10.30. 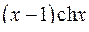 .
.
10.31. 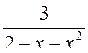 .
.
ЛИТЕРАТУРА
1. Шипачев В.С. Высшая математика. Учебник для вузов. М.: Высшая школа, 2005.
2. Письменный Д.Т. Конспект лекций по высшей математике. М.: Айрис-Пресс, 2005.
Дата: 2018-12-21, просмотров: 327.