Площадь криволинейной трапеции, ограниченной кривой, заданной функцией 
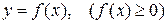, прямыми 
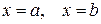и отрезком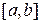 
Оси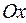 
, вычисляется по формуле:
.
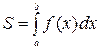Площадь криволинейной трапеции, верхняя граница которой задана параметрически, вычисляется так:
,
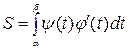где верхняя граница: х=j(t), y=y(t), a£t£b.
Площадь фигуры ограниченной двумя непрерывными линиями (рис. 1) равна
,
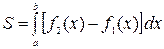где S – площадь криволинейной трапеции, ограниченной графиками функций y=f1(x) и y=f2(x), (f1(x)³f2(x)), прямыми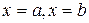 
(a<b).
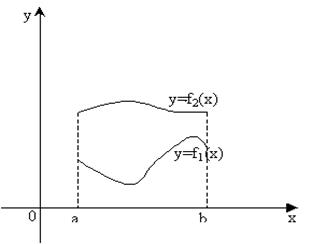
рис.5.1.
Площадь криволинейного сектора в полярной системе координат
,
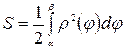здесь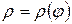 
- кривая, заданная в полярной системе координат, a£j£b.
Вычисление длины дуги кривой.
,
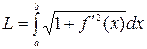где L – длина кривой, заданной уравнением y=f(x), a£x£b.
,
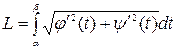где L – длина кривой, заданной параметрическими уравнениями х=j(t), y=y(t), a£t£b.
,
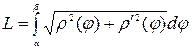где L – длина кривой, заданной в полярной системе координат уравнением r=r(j), a£j£b.
Формулы объемов тел вращения
,
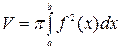где V – объем тела, полученного вращением криволинейной трапеции 0£y£f(x), a£x£b вокруг оси Ох.
,
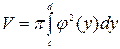где V – объем тела, полученного вращением криволинейной трапеции 0 £ x £ j ( y ), c £ y £ d вокруг оси Оy.
Формулы площадей поверхностей вращения
,
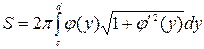где S – площадь поверхности, образованной вращением кривой, заданной уравнением x=j(y), с£у£d, вокруг оси Оу.
,
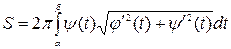где S – площадь поверхности, образованной вращением кривой, заданной параметрическими уравнениями x=j(t), y=y(t), a£t£b.
,
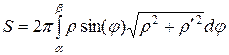где S – площадь поверхности, образованной вращением кривой, заданной уравнением в полярных координатах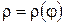 
, a£j£b.
Пример5.1 Найти площадь фигуры ограниченной линиями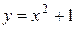 
и 
.
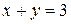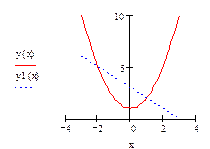
Решение: На рис. 2 представлена фигура площадь которой требуется найти.
Найдем точки пересечения параболы и прямой для этого решим следующую систему уравнений:
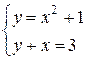Þ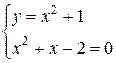 
При решении квадратного уравнения системы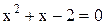 
, получаем два корня х1=-2, х2=1.
рис. 2.
f1(x)= x2+1, f2(x)=3-x (т.к. прямая лежит выше параболы в рассматриваемой области).
Теперь можно вычислить площадь фигуры: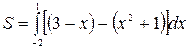 
= 
= = 
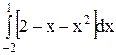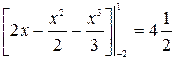
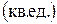
Пример 5.2 Найти площадь фигуры, ограниченной кривыми:
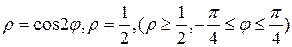
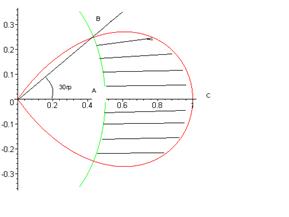рис.3.
В силу симметричности заштрихованной фигуры, ее площадь
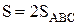Найдем угол, который образует луч ОВ с полярной осью:
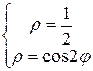
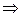
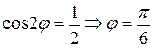
Согласно формуле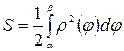 
, имеем:
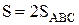=2 
= 
= 
= 
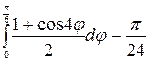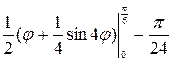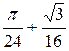
Пример 5.3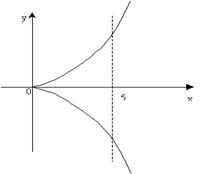 
Найти длину дуги полукубической параболы 
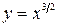от х=0 до х=5 (рис. 4).
Решение: Кривая симметрична относительно оси Ох. Найдем длину верхней ветви кривой. Из уравнения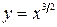 
находим 
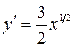. Далее, применяя формулу 
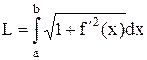получим
= 
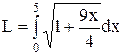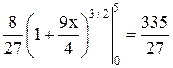(ед.)
рис.4.
Пример 5.4 Найти длину дуги кривой, заданной параметрически:
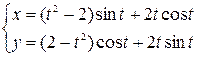
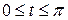
Решение.
Воспользуемся формулой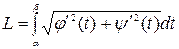 
. Для чего найдем
= 
= 
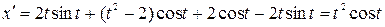
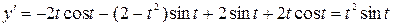
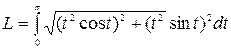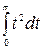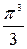
Пример 5.5 Найти объем тела, образованного вращением вокруг оси Oy плоской фигуры, ограниченной кривыми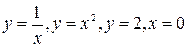 
Решение.
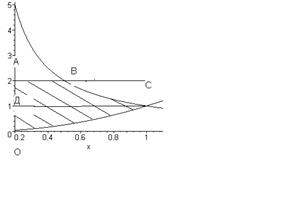
рис5
Так как плоская фигура вращается вокруг оси Oy , то за независимую переменную надо выбрать y.Применим формулу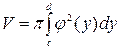 
Искомый объем есть сумма объемов двух тел, одно из которых получено вращением вокруг оси Oy криволинейной трапеции ОДС, другое – вращением криволинейной трапеции АВСД
Поэтому
= 
= 
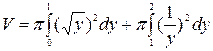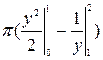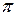
Пример 5.6 Найти площадь поверхности, образованной вращением кардиоиды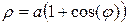 
(см. рис.6) вокруг полярной оси.
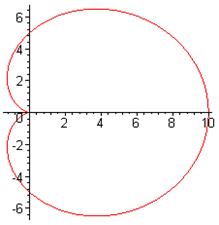
рис.6
Решение: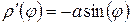 
, 
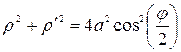Þ по формуле
= 
= = 
= 
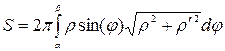
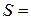
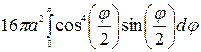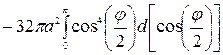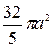(ед. кв.)
II. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.
Дата: 2018-12-21, просмотров: 216.
