Интегралы вида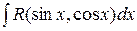 
, где R –рациональная функция от двух переменных, сводится к интегралам от рациональных функций одной переменной при помощи универсальной тригонометрической подстановки:
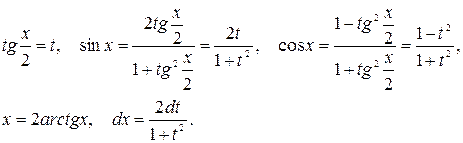(3.1)
Однако в большинстве случаев предпочтительнее воспользоваться рассмотренными ниже частными подстановками:
1).Если 
- нечетная функция относительно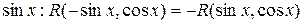 
, то интеграл вычисляется с помощью подстановки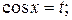 
2).Если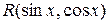 
- нечётная функция относительно 
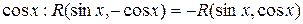, то используется подстановка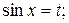 
3).Если 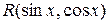- четная функция относительно 
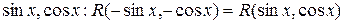, то интеграл вычисляется с помощью подстановки 
;
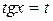Интегралы вида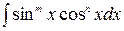 
вычисляются следующим образом:
При n – нечётном положительном числе применима подстановка 
, если m – нечётное положительное число, то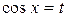 
, если же m , n – чётные положительные числа, тогда используют формулы:
Интегралы вида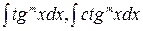 
, m – целое положительное число, решаются при помощи замены 
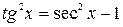или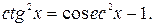 
Интегралы вида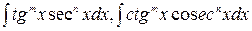 
, где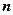 
- целое положительное число, вычисляются при помощи замены :
.
Для интегралов вида
используются рекуррентные формулы :
.
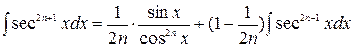
При вычислении интегралов вида
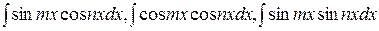
используют известные соотношения:
.
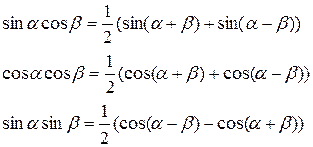Пример 3.1 Вычислить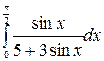 
.
Решение.
Используем универсальную подстановку:
= 
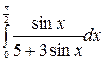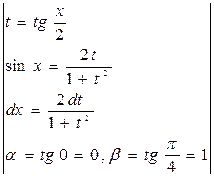
= 4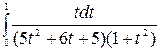 
.
Разложим подынтегральную рациональную дробь на простейшие и получим:
4 = -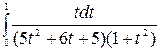 
=
=- 
= 
=
= 
.
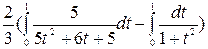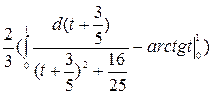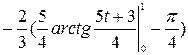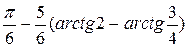Пример3.2 Вычислить 
.
Решение.
= 
.
Подынтегральная функция четная относительно 
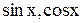, поэтому используем подстановку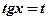 
= 
= 
= = 
= = 
= 
.
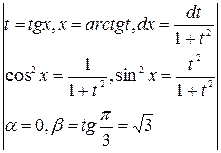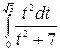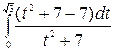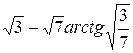Пример 3.3 Найти 
.
Решение.
Подынтегральная функция нечетна относительно 
. Сделаем замену 
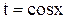. Тогда
= 
= 
= 
=
= 
= 
= 
.
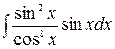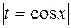Интегрирование простейших иррациональных функций.
Интегралы вида
(4.1)
где R-рациональная функция своих аргументов
m 1, n 1, m 2, n 2,… целые числа, вычисляются с помощью подстановки 
, (4.2)
где S-общий знаменатель дробей: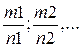 
При вычислении интегралов вида: 
, где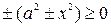 
удобно использовать тригонометрические подстановки:
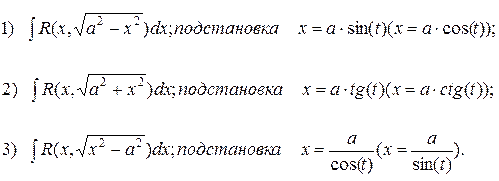
Выражение вида
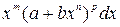, где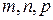 
- рациональные числа, 
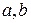- действительные числа, называется биномиальным дифференциалом.
Интеграл от биноминального дифференциала
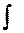
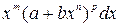
сводится к интегралу от рациональной функции только в следующих случаях:
1). 
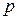-целое, подстановка вида (4.2);
2). 
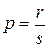– дробное и 
- целое, тогда интеграл от биномиального дифференциала рационализируется подстановкой: 
(первая подстановка Чебышева);
3). 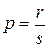– дробное и 
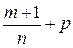- целое, тогда применяется подстановка 
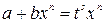(вторая подстановка Чебышева).
Пример 4.1. Вычислить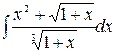 
Решение.
= 
= 
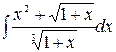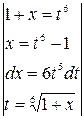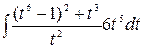=6 
= = 
.
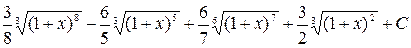Пример 4.2 Вычислить 
.
Решение.
= 
= 
=
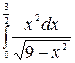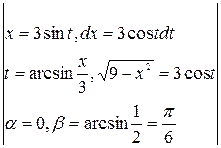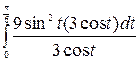=9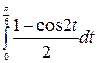 
= 
= 
.
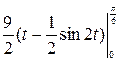Пример 4.3 Вычислить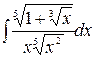 
.
Решение.
= 
,
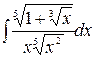по условию 
. Число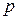 
дробное, а 
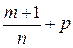=-1-целое. Поэтому будем использовать вторую подстановку Чебышева.
= 
=
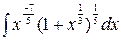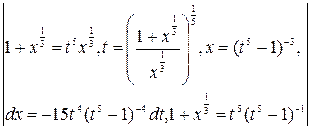=-15 
=-15 
=- 
=- 
.
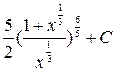Приложения определенных интегралов.
Дата: 2018-12-21, просмотров: 237.
