Пусть 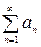 (1.2) и  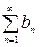 (1.3) – знакоположительные ряды, то есть,  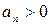и .

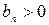Первый признак сравнения. Если существует такое число N, что для всех n>N выполняется неравенств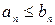о , то

1) из сходимости ряда (1.3) следует сходимость ряда (1.2);

2) из расходимости ряда (1.2) следует расходимость ряда (1.3).

Второй признак сравнения. Если существует конечный предел , то ряды (1.2) и (1.3) сходятся или расходятся одновременно.

Признак Даламбера. Если существует 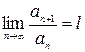, то:

1) при 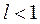 ряд (1.2) сходится;

2) при 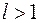 ряд (1.2) расходится;

3) при 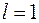 признак не решает вопроса о сходимости ряда.

Признак Коши. Если существует 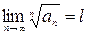, то:

1) при 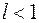 ряд (1.2) сходится;

2) при 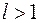 ряд (1.2) расходится;

3) при 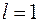 признак не решает вопроса о сходимости ряда.

Интегральный признак. Если для ряда (1.2) существует функция 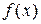 такая, что на промежутк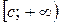е , где :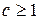

1) непрерывна; 2) не возрастает; 3) 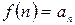 при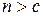  

то ряд (1.2) и 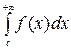 сходятся или расходятся одновременно.

Замечания.

1) При использовании признаков сравнения обычно применяются следующие ряды:

обобщенный гармонический 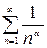, который при  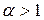сходится, при

расходится;

геометрический ряд , , 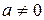который сходится при  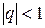и расходится при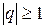

2) Полезно помнить теорему о замене эквивалентных бесконечно малых в пределах, в том числе таблицу эквивалентных бесконечно малых, при : , , , , , , , , , .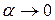

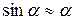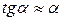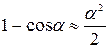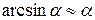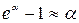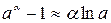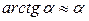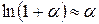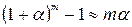3) Если общий член ряда содержит факториалы, то к исследованию ряда на сходимость обычно применяют признак Даламбера; если содержит n-ые степени – то признак Коши.

Пример 1.3. Исследовать на сходимость ряд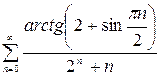

Используя ограниченность функций 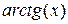,  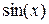и свойства дробей, имеем:

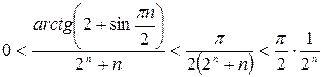
Ряд 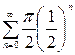 сходится как геометрический со знаменателем 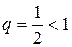. В силу полученного неравенства и первого признака сравнения исходный ряд сходится.

Пример 1.4. Исследовать на сходимость ряд

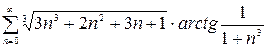
Используя известную эквивалентность:

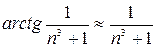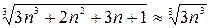и , при ,

подберем ряд для сравнения:

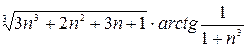
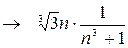
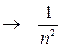
Рассмотрим ряд 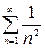 - это есть обобщенный гармонический ряд с  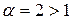следовательно сходящийся.

Применим к ряду 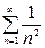 и к исходному ряду  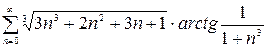второй признак сравнения.

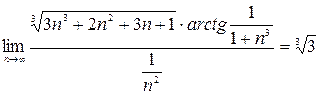
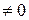- ряды имеют одинаковый характер сходимости, а значит исходный ряд сходится.

Пример 1.5. Исследовать на сходимость ряд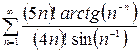

Очевидно, что этот ряд знакоположительный, применим к нему признак Даламбера:

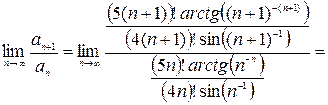
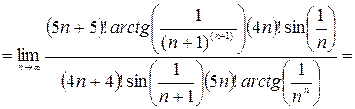
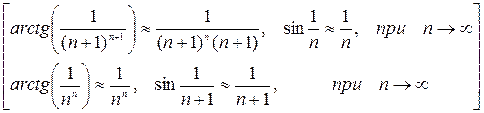
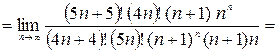
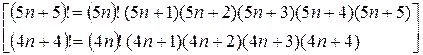
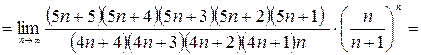
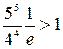
По признаку Даламбера ряд расходится.

Пример 1.6. Исследовать на сходимость ряды:

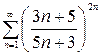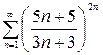а) , б) , в)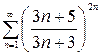

Решение.

а) Применим признак Коши к ряду :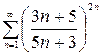

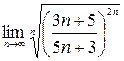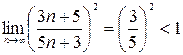= , данный ряд сходится.

б) Применим признак Коши к ряду :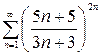

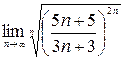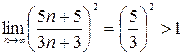= , данный ряд расходится.

в) Применим признак Коши к ряду :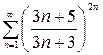

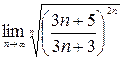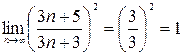= , вопрос о сходимости данного ряда открыт. Применяем другие признаки, например необходимый признак сходимости. Для этого найдем предел общего члена данного ряда, имеем:

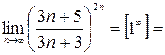
0, ряд расходится (не выполняется необходимый признак сходимости).

Пример 1.7. Исследовать на сходимость ряд: .

Рассмотрим ряд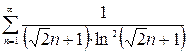  

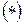
Применим к исходному ряду и ряду 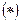 второй признак сравнения:

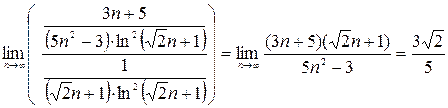
Эти ряды имеют одинаковый характер сходимости, сходятся или расходятся одновременно.

Применим к ряду 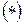 интегральный признак сходимости.

Функция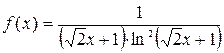  

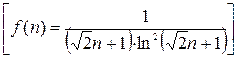
удовлетворяет на 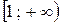 всем условиям интегрального признака сходимости.

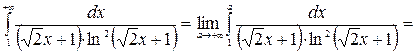
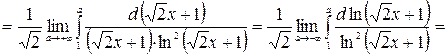
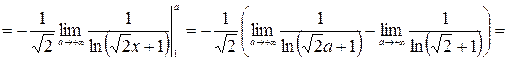
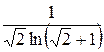- несобственный интеграл сходится.

На основании интегрального признака утверждаем, что ряд 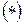 сходится, а значит сходится и исходный ряд.