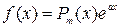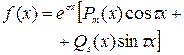Уравнение вида 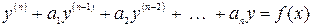 (3.1)
(3.1)
где 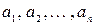 - действительные числа, называется линейным дифференциальным уравнением (ЛДУ) с постоянными коэффициентами. Если
- действительные числа, называется линейным дифференциальным уравнением (ЛДУ) с постоянными коэффициентами. Если 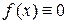 , то уравнение (3.1) называется однородным (ОЛДУ), в противном случае – неоднородным (НЛДУ).
, то уравнение (3.1) называется однородным (ОЛДУ), в противном случае – неоднородным (НЛДУ).
Общее решение ОЛДУ строится с учётом корней алгебраического уравнения 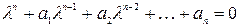 (3.2), называемого характеристическим уравнением для ЛДУ (3.1).
(3.2), называемого характеристическим уравнением для ЛДУ (3.1).
Каждому действительному корню и каждой паре мнимых сопряжённых корней характеристического уравнения в общем решении ОЛДУ соответствует слагаемое, определяемое таблицей 3.1.
Таблица 3.1.
| Вид корней характеристического уравнения | Вид слагаемого в общем решении ОЛДУ |
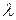 - действительный корень кратности 1 - действительный корень кратности 1
| 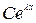
|
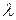 - действительный корень кратности - действительный корень кратности 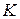
| 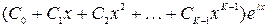
|
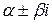 - пара мнимых корней кратности 1 - пара мнимых корней кратности 1
| 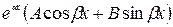
|
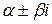 - пара мнимых корней кратности - пара мнимых корней кратности 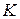
| 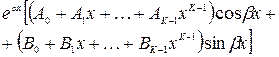
|
Здесь 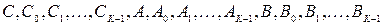 - произвольные постоянные. Напомним что общее решение дифференциального уравнения порядка
- произвольные постоянные. Напомним что общее решение дифференциального уравнения порядка 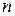 содержит
содержит 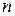 произвольных констант.
произвольных констант.
Пример 3.1. Найти решение ОЛДУ
а) 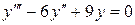 (3.3)
(3.3)
Записываем характеристическое уравнение: 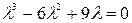 Û
Û  . Его корни:
. Его корни: 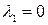 - кратности 1,
- кратности 1, 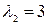 - кратности 2. Первому корню в общем решении соответствует слагаемое
- кратности 2. Первому корню в общем решении соответствует слагаемое 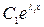 , то есть
, то есть 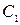 , второму -
, второму - 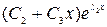 , то есть
, то есть 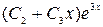 . Общее решение ОЛДУ:
. Общее решение ОЛДУ: 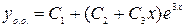 .
.
б) 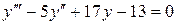 (3.4)
(3.4)
Характеристическое уравнение :
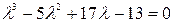 Û
Û 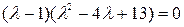
Его корни: 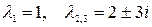 - все кратности 1. Им соответствуют в общем решении ОЛДУ слагаемые
- все кратности 1. Им соответствуют в общем решении ОЛДУ слагаемые 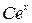 и
и 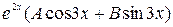 .
.
Итак 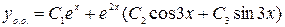 .
.
Для нахождения общего решения неоднородного уравнения (3.1) используем теорему о структуре общего решения НЛДУ: 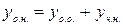 , где
, где 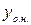 - общее решение НЛДУ,
- общее решение НЛДУ, 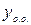 - общее решение соответствующего ОЛДУ,
- общее решение соответствующего ОЛДУ, 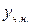 - какое-нибудь частное решение НЛДУ. Нахождение
- какое-нибудь частное решение НЛДУ. Нахождение 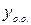 описано выше. Для нахождения
описано выше. Для нахождения 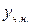 будем использовать метод подбора. Этот метод применим в случае, когда правая часть
будем использовать метод подбора. Этот метод применим в случае, когда правая часть 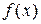 уравнения (3.1) имеет специальный вид. В таблице 3.2. для некоторых случаев указано, в каком виде следует искать частное решение НЛДУ.
уравнения (3.1) имеет специальный вид. В таблице 3.2. для некоторых случаев указано, в каком виде следует искать частное решение НЛДУ.
Таблица 3.2.
| Вид правой части | Связь с корнями характеристического уравнения | Вид частного решения |
|
| 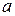 - не корень характ. Уравнения - не корень характ. Уравнения
| 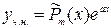
|
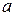 - корень характ. Уравнения кратности К - корень характ. Уравнения кратности К
| 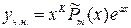
| |
|
| 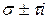 - не корни характ. Уравнения - не корни характ. Уравнения
| 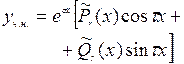
|
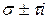 - корни характ. Уравнения кратности К - корни характ. Уравнения кратности К
| 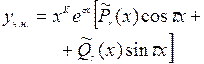
|
Здесь 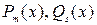 - заданные многочлены,
- заданные многочлены, 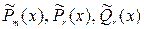 - многочлены с неопределёнными коэффициентами; индекс указывает степень многочлена,
- многочлены с неопределёнными коэффициентами; индекс указывает степень многочлена, 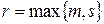 .
.
Пример 3.2. Найти общее решение НЛДУ.
а) 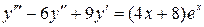 (3.5)
(3.5)
Общее решение соответствующего ОЛДУ найдено в примере 3.1.: 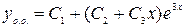 . Правая часть данного уравнения имеет вид
. Правая часть данного уравнения имеет вид 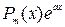 , m=1, a=1. Так как a=1 не корень характеристического уравнения, то
, m=1, a=1. Так как a=1 не корень характеристического уравнения, то 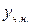 ищем в виде:
ищем в виде: 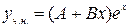 . Для нахождения неопределённых коэффициентов А и В подставим эту функцию в уравнение (3.5). В результате подстановки получим:
. Для нахождения неопределённых коэффициентов А и В подставим эту функцию в уравнение (3.5). В результате подстановки получим: 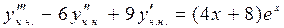 , то есть
, то есть
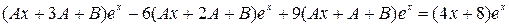 . Сокращаем обе части равенства на
. Сокращаем обе части равенства на 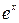 и приравниваем коэффициенты при одинаковых степенях х в левой и правой частях: 4А=4, 4В=8 Þ А=1, В=2.
и приравниваем коэффициенты при одинаковых степенях х в левой и правой частях: 4А=4, 4В=8 Þ А=1, В=2.
Итак: 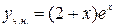 , а
, а 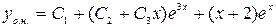 .
.
Замечание. Для проверки правильности нахождения частного решения рекомендуется подставить найденное  в исходное уравнение: решение найдено верно, если в результате такой подстановки получим тождество.
в исходное уравнение: решение найдено верно, если в результате такой подстановки получим тождество.
б) 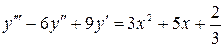 (3.6)
(3.6)
Правая часть имеет вид 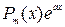 , причём m=2, a=0. Нуль является корнем характеристического уравнения кратности 1. Поэтому
, причём m=2, a=0. Нуль является корнем характеристического уравнения кратности 1. Поэтому 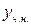 ищем в виде:
ищем в виде:  , то есть
, то есть 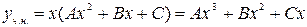 . Подставляем в исходное уравнение и приводим подобные:
. Подставляем в исходное уравнение и приводим подобные:
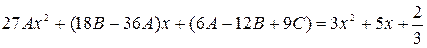 , отсюда
, отсюда
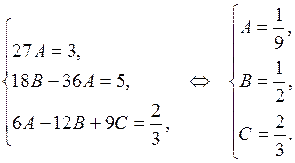
Следовательно 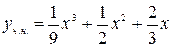 .
.
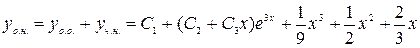 .
.
в) 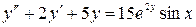 .
.
Находим общее решение соответствующего ОЛДУ, для чего решаем характеристическое уравнение 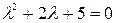 . Его кони
. Его кони 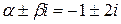 кратности 1, поэтому
кратности 1, поэтому 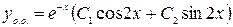 (см. таблицу 3.1).
(см. таблицу 3.1).
Правая часть НЛДУ имеет вид 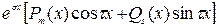 , причём
, причём 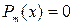 ,
,  ,
, 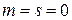 ,
, 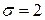 ,
, 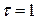 . Так как
. Так как 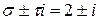 не корни характеристического уравнения, то, согласно таблице 3.2,
не корни характеристического уравнения, то, согласно таблице 3.2,  ищем в виде:
ищем в виде: 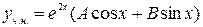 ,
, 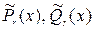 - многочлены нулевой степени с неопределёнными коэффициентами. Находим
- многочлены нулевой степени с неопределёнными коэффициентами. Находим 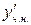 ,
, 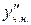 и, подставляя в исходное уравнение, приводим подобные:
и, подставляя в исходное уравнение, приводим подобные:
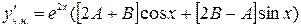 ,
, 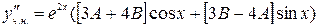 ,
,
 .
.
Сокращаем обе части на 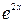 и приравниваем коэффициенты при
и приравниваем коэффициенты при 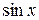 и
и 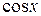 в левой и правой частях:
в левой и правой частях:
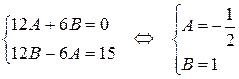 , значит
, значит 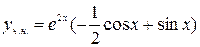 ,
,
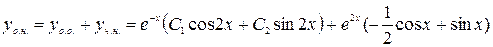 .
.
Метод подбора применим и в том случае, когда правая часть уравнения (3.1) не имеет вида, представленного в таблице 3.2, но является суммой функций такого вида. Согласно теореме суперпозиции, если  есть решение ЛНДУ
есть решение ЛНДУ 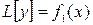 , а
, а 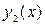 - решение ЛНДУ
- решение ЛНДУ 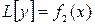 , то
, то 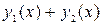 есть решение ЛНДУ
есть решение ЛНДУ 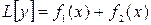 .
.
Поэтому для нахождения частного решения последнего уравнения достаточно найти какие-нибудь частные решения двух предыдущих уравнений и сложить их.
Пример 3.3. Найти общее решение НЛДУ 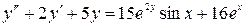 .
.
Здесь 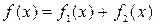 ,
, 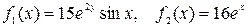 .
.
Для уравнения 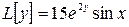 частное решение найдено в примере 3.2(в):
частное решение найдено в примере 3.2(в):
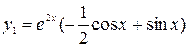 . Найдём
. Найдём 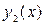 - частное решение уравнения
- частное решение уравнения 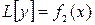 , то есть
, то есть 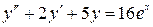 (3.7)
(3.7)
Правая часть этого уравнения имеет вид 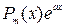 , причём m=0, a=1. Так как a=1 не является корнем характеристического уравнения, то
, причём m=0, a=1. Так как a=1 не является корнем характеристического уравнения, то 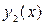 ищем в виде:
ищем в виде: 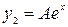 . Подставляя
. Подставляя 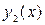 в (3.7), легко найдём А=2.
в (3.7), легко найдём А=2.
Итак 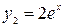 и
и 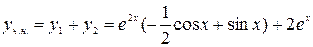 ,
,
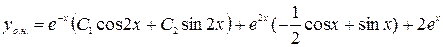 .
.
Дата: 2018-12-21, просмотров: 370.