Высшей формой теоретического знания считается научная теория. На стадии зарождения научная теория не является автономной и общепринятой системой. Стадия зрелости, завершенности теории характеризуется оформленностью основных принципов, основного содержания теории, практикой применения к решению различных познавательных задач.
В. Гёйзенберг следующим образом разъясняет свое понимание зрелой научной теории применительно к физике: «Под завершенной теорией мы понимаем систему аксиом, определений и законов, с помощью которых становится возможным правильно и непротиворечиво описать, то есть представить в математической форме, большой круг феноменов» [25. С. 1291. Гёйзенберг поясняет, что аксиомы теории используются для установления связи основных понятий теории. После аксиоматизации понятия приобретают «жесткость» и отрываются от опыта, что и ограничивает их применимость. Аксиомы завершенной теории переводятся на язык математики. Математизированная зрелая теория превращается в последовательность мыслительных структур как чисто
69
интеллектуальных образований и идеализации опыта. При этом замкнутая непротиворечивая завершенная теория сама по себе не содержит вполне достоверных утверждений о мире опыта. К числу зрелых физических теорий В. Гейзенберг относит классическую механику Ньютона, статистическую теорию теплоты, специальную теорию относительности (включая электродинамику), волновую квантовую механику.
Зрелая научная теория в идеале представляет собой логически организованную, обычно открытую (развивающуюся) систему понятий, высказываний, проблемных вопросов, непосредственно относящихся к соответствующим идеализированным объектам. Каждая теория имеет свою онтологию, и высказывания теории характеризуют фундаментальные «сущности» (объекты) предметной области теории. В теорию включаются также вспомогательные высказывания, в частности «семантические предположения», которые обрисовывают онтологическое значение терминов, формул и т. п. Элементами теории являются также различные определения как лингвистические конвенции относительно значения терминов, символов. Если теория математизирована, то в ней выделяют формальные (математические) термины и высказывания. Каждая теория имеет конкретно-научную методологию, которая указывает, какие вопросы (проблемы) ученый может ставить в отношении фундаментальных сущностей предметной области теории, какие конкретно-научные методы обычно используются для решения поставленных задач.
Абстрактные (общие) теории ограничиваются строго универсальными и чисто экзистенциальными высказываниями и входящими в них теоретическими терминами. Предметом абстрактных (общих) теорий как раз и являются идеализированные умственные объекты как таковые. Общие теории не связаны с какими-либо специфическими видами наблюдательных экспериментальных установок для эмпирического познания объектов. Конкретная -(специальная) теория содержит концептуальные модели рассматриваемых теорией «сущностей». В общем случае концептуальная модель представляет собой некоторый перечень признаков объектов, указывающий на природу изучаемых объектов, предположительный вид их взаимодействия и др. Конкретные теории возникают обычно путем присоединения к абстрактной теории концептуальных моделей, конкретизирующих, специфицирующих теоретические объекты, в той или иной мере приближающих их к эмпирически существующим объектам. Подсоединение концептуальных моделей иногда трактуется в смысле интерпретации
абстрактных теорий. Концептуальная модель грубо специфициру-ет изучаемые объекты, уточняет основные положения общей теории, выполняет эвристическую функцию для обеспечения терминов и высказываний общей теории фактуально-онтологическими значениями.
Для понимания онтологии теорий важно иметь в виду, что строго универсальное высказывание формы «Всем объектам х принадлежит характеристика Р» (простое символическое представление в виде V х Р(х)) эквивалентно чисто экзистенциальному высказыванию формы «Неверно, что существуют объекты х с характеристикой не-Р» (упрощенное символическое представление в виде —3 x— iP( x)), а чисто экзистенциальное высказывание формы «Существуютобъекты хсхарактеристикой Р» (упрощенноесимволическое представление в виде Эх Р{х)) эквивалентно строго универсальному высказыванию формы «Неверно, что все объекты х имеют характеристику не-Р» (упрощенная символическая запись в виде—iVx—\ P( x)). С учетом указанных эквивалентностей общую научную теорию можно выразить как в форме совокупности утверждений вида VxP ( x) и ЗхР(х), так и в эквивалентной форме совокупности отрицаний вида—>Vx—iP(x) и Sx— iP( x). В случае выражения теории в форме совокупности утверждений теория «разрешает» (допускает) утверждаемые положения дел в своей предметной области, в случае выражения теории в форме совокупности отрицаний теория «запрещает» (не допускает) отрицаемые положения дел в своей предметной области.
Наиболее значимыми онтологическими высказываниями теории считаются формулировки законов, которые являются главным средством соотнесения элементов теории с действительностью. Закон науки — это зафиксированное в языке знание общей и необходимой повторяемости, или регулярности. Законы науки, как элементы научной теории, характеризуются определенной мерой точности, огрубления действительности. Если некоторая регулярность относится ко всем пространственно-временным областям действительности (ко всем «возможным мирам»), она считается универсальным законом (пример: любой кусок льда в любом месте во Вселенной и в любое время является холодным) и фиксируется в форме строго универсального условного высказыванием типа Vx(F(x) —» С(х)).Если х обозначает любое материальное тело, тогда закон может состоять в утверждении: для любого материального тела х, если хобладает свойством F, то он обладает также свойством G. В физике, например, мы можем сказать: «Для каждого тела х, если это тело нагревается, то оно
71
будет расширяться». Это закон теплового расширения в простейшей, неколичественной форме. В науке, конечно, стремятся выявить количественные законы и характеризуют их так, чтобы не допустить исключений. Универсальные высказывания называются «законами» и в более элементарных случаях, как, например, в случае утверждения «Все вороны — черные».
Выделяют два вида законов науки — эмпирические и теоретические. Законы простого вида иногда называют «эмпирическими обобщениями» или «эмпирическими законами». Они называются простыми, потому что говорят о свойствах, которые можно наблюдать (например, черный цвет или магнитные свойства куска железа). Например, закон теплового расширения представляет собой обобщение результатов многих наблюдений тел, которые расширяются при нагревании.
Выраженная научным законом регулярность, конечно, не наблюдается непосредственно (в смысле единичного локального наблюдения). Она обнаруживается только при сравнении многих единичных наблюдений друг с другом. В результате сравнения формулируется высказывание универсального типа. Можно было бы согласиться с утверждением Э. Маха, что общие законы (физики), представленные универсальными высказываниями, «ничем существенным не отличаются от описания» бесчисленного множества фактов. Однако с мыслью Маха о том, что закон науки вовсе не имеет более существенного значения, чем все представляемые законом отдельные факты вместе взятые, согласиться невозможно: «взять вместе» бесконечное множество фактов невозможно. Другими словами, строго универсальное высказывание о бесконечном множестве объектов не может сводиться к конъюнкции единичных высказываний о соответствующих объектах познания и не может доказываться перебором таких объектов. В этом смысле закон выходит за границы множества познанных отдельных фактов.
Далеко не все научные положения выражают законы. Высказывание «Вчера в полночь над городом N пролился ливень» не является фиксацией закона. Оно говорит, что нечто случилось в такое-то время и в таком-то месте. Поскольку такие утверждения, как это, являются эмпирическими утверждениями об отдельных фактах, их называют «единичными», «частными», «сингулярными», «протокольными» высказываниями. Одним из больших и сложных вопросов философии науки является вопрос о том, как осуществляется подъем познания от единичных высказываний к универсальным законам науки. В общем плане можно сказать, что указанный
72
подъем осуществляется с помощью различных форм обобщения (специальному рассмотрению научная индукция как форма обобщения подвергается ниже). В ходе такого обобщения существенное значение имеет проблема истинности, «добротности» взятых за базу обобщения единичных высказываний (единичных случаев). Об этом свидетельствует драматический пример Грегора Менделя.
Исследуя горох, а также фасоль, левкои, кукурузу и другие растения, Мендель сделал заявку на некую закономерность: во втором поколении гибридные (появившиеся в результате скрещивания различных сортов и разновидностей) растения появляются как с доминантными (подавляющими), так и рецессивными (подавляемыми) признаками исходных растений в пропорции 3:1. Мендель счел, что его закон универсален в смысле распространения на все растения. Но из обобщения Менделя закона не получилось, поскольку регулярность не выполнялась в случае растения иод названием ястребинка. Лишь много лет спустя было установлено, что ястребинка, в отличие от исследованных Менделем растений, размножается без опыления и оплодотворения, то есть не поддается гибридизации. Неудачная подборка базиса менделевского обобщения не позволила правильно сформулировать общезначимый закон, который ограничивается лишь гибридными растениями.
Теории обычно излагаются одним из трех взаимно дополнительных способов — историческим, эвристическим, аксиоматическим. При историческом изложении выделяют основную проблему теории и анализируют различные исторически сменяющие друг друга попытки ее решения (включая ошибочные), выделяя изложение пути к «правильному» решению проблемы. Эвристический способ характеризуется выделением наиболее полезных, хотя и не обязательно наиболее фундаментальных положений теории, выведением следствий из выделенных положений, применением этих следствий для решения каких-либо задач. При аксиоматическом способе выделяются основные понятия теории, внутри теории не определяемые, и основные положения, внутри теории не доказываемые, а затем развертываются процессы определения на базе основных всех других понятий теории, доказательства на базе основных всех других положений теории. В каждой хорошо построенной аксиоматической теории фигурируют формальные (математические), семантические (смысловые), материальные (объектные) постулаты. О значении формальных и семантических постулатов говорилось выше. Объектные постулаты характеризуют объекты теории, формулируют, в частности, их законы.
73
Обычно хорошо развитая теория строится в виде гипотетико-дедуктивной системы, в которой из группы начальных понятий и высказываний, образующих собственный базис теории, с помощью логики и математики выводятся другие понятия и высказывания теории. Идеалом здесь являются дедуктивно замкнутые системы, в которых с помощью логики из начальных предложений получаются все выполнимые в предметной области теории высказывания. Множество понятий, полученных с помощью определений из базисных понятий, и высказываний, полученных с помощью логики из базисных высказываний, иногда называют «телом» теории.
Научные теории формируются в широком культурном контексте. Элементы культуры, играющие определенную роль в формировании теорий, называются основаниями теории, которые отличны от собственных (внутренних) оснований теории, представленных исходными неопределяемыми понятиями и исходными недоказываемыми положениями теории. О предшествующих теории научных результатах, касающихся предметной области теории, говорят как об исторических основаниях теории. Эмпирическими основаниями теории называют совокупность эмпирических данных, фактов, повлиявших на формирование теории. Эмпирические основания имеются лишь у специальных теорий, они отсутствуют у абстрактных и формальных теорий. К философским основаниям научной теории относятся философские положения, на которых базируется научная теория. Философские основания включают онтологические (в широком философском смысле слова), гносеологические, логические, социологические предпосылки научной теории. Философско-онтологические основания представлены обычно общими положениями философской концепции бытия (онтологии, философской картины мира). Это может быть холистский принцип выведения свойств и характеристик простых объектов предметной области из характеристик целостных систем, элементами которых являются простые объекты. Это может быть номиналистская установка на выведение свойств и характеристик целостных систем объектов из свойства элементов таких систем.
В этот же круг онтологических положений входят признание или отклонение принципов эволюционного рассмотрения объектов, качественной и количественной неисчерпаемости видов объектов и их свойств, субстанциальной или реляционной трактовки природы пространства и времени, идей бесконечности пространства и времени, причинной организации мира, самоорганизации систем и т. д. Гносеологические основания научной теории
74
сводятся, в частности, к допущениям, определяющим меру упрощения, огрубления, идеализации изучаемых объектов. Например, при образовании понятия «физическая точка» принимается допущение, что рассматриваемый объект имеет всего две характеристики — массу и пространственные координаты. При образовании понятия «математическая точка» отвлекаются и от массы тела. В последнем случае мера идеализации выше в сравнении с первым. Принятые в теории огрубления и идеализации действительности определяют истинность или ложность, правдоподобность или неправдоподобность положений теории и т. п. Логические основания теории — это законы и правила логики, принятые в теории. Логика не дает конкретной, частной информации о предметной области теории. Она дает информацию о логических отношениях между терминами и высказываниями теории и о логических операциях над ними. Задача логических оснований усматривается в том, чтобы получаемые из собственных оснований с помощью логики новые термины и высказывания имели бы ту же меру огрубления и идеализации действительности, которая установлена гносеологическими основаниями.
Не всякая логическая система способна сохранить для всех элементов теории одну и ту же меру огрубления и идеализации. Для каждой заданной теории надо выбирать подходящую, соответственную, релевантную теории систему логики. Избранная логика обеспечивает также логическую истинность сложных высказываний теории, поскольку значение истинности таких высказываний рассматривается в качестве функции значений истинности входящих в сложное высказывание «элементарных» высказываний. Логика, принятая в теории, является средством доказательства выводимых высказываний теории, обоснования их истинности.
Примером философских оснований является концепция «умеренного аристотелевского реализма» Г. Кантора, которую он предпосылает классической теоретико-множественной математике (см. [122]). Исходным моментом канторовской концепции является различение интрасубъективного (имманентного) и транссубъективного (транзиентного) существования математических понятий (объектов). Под имманентным существованием Кантор имеет в виду существование математических понятий внутри человеческого сознания. Во внутреннем мире сознания математические понятия занимают определенное место и находятся друг к другу в определенных отношениях.
Для имманентного существования понятия, согласно Кантору, необходимы два условия: «в себе» непротиворечивость и упоря-
75
доченгюсть отношений к ранее образованным понятиям [122. S. 3741. Всякое вновь вводимое математическое понятие обладает имманентным существованием, если оно удовлетворяет указанным условиям. Математические понятия принимаются Кантором за выражение (отражение) явлений противостоящего интеллекту внешнего мира [Там же. S. 181]. Например, такие математические объекты, как числа, суть «репрезентанты мощностей, встречающихся в телесной и духовной природе». Существование репрезентантов (прообразов) математических объектов в реальной действительности Кантор истолковывает как транзиентное существование математических понятий. При этом всякое математическое понятие всегда в известных, даже бесконечно многих отношениях обладает также транзиентной реальностью [Тамже. S. 18^.Установление транзиентной реальности математических понятий принадлежит, согласно Кантору^, «к наиболее трудным и тяжелым задачам метафизики и часто должно откладываться до тех нор, пока развитие одной из других наук не обнаружит транзиентное значение соответствующего понятия» [Тамже. S. 182].
Математические объекты (числа, функции, множества и др.), существующие транзиентно, независимо от мышления людей и возможных способов их познания, образуют универсальную область, в которой в готовом виде, «в себе» существуют объемы всех имманентно существующих понятий математики. Простое введение имманентно существующего понятия в этом смысле есть «открытие» существующего «самого по себе» положения вещей во внешнем мире.
Сущность чистой математики, по мнению Г. Кантора, «лежит непосредственно в ее свободе», а свобода состоит во введении имманентно существующих математических понятий без специального подтверждения их транзиентной реальности. Транзиентная реальность этих понятий просто всегда предполагается, но непосредственно в математике не устанавливается. К числу таких понятий классической математики Кантор относит и понятие актуальной (завершенной) бесконечности [Там же. S. 375]. Таковы канторовские философские основания классической математики.
Другим примером философских оснований научных теорий является концепция, разработанная основателем так называемой интуиционистской математики Л. Брауэром. Позиция Брауэра по вопросу о философских основаниях интуиционистской математики эволюционировала. Мы рассмотрим эту позицию на период закладки основ интуиционистской математики в начале XX столетия. В 1907 г. была опубликована докторская диссертация Брауэра
76
«Об основаниях математики» [ 121 ], в которой автор в сжатом виде изложил онтологические и гносеологические основания естественно-научного и математического познания. Человек, согласно Брауэру, имеет дело со спонтанно протекающими природными событиями и процессами, среди которых выделяет повторяющиеся последовательности причинно связанных событий. Заключительные элементы таких последовательностей человек использует для удовлетворения своих потребностей.
Полезные последовательности служат основой для выработки соответствующих правил поведения человека. Первоначально правила имеют эмпирический характер, ограничены, надежны лишь в очень узких рамках. Своей деятельностью человек стремится расширить сферу применения и надежность найденных правил. Достигает он этого путем своего воздействия на условия существования природных последовательностей, изолируя спонтанно разворачивающиеся последовательности от побочных разрушающих, возмущающих факторов. В результате «человек делает все в природе более закономерным, чем это имеет место само по себе спонтанно» [Там же. F. 82].
Средством усмотрения природных последовательностей является фигура сознания, которую Брауэр назвал интуицией времени. Интуиция времени схватывает изменение, осуществляемое в форме «вещь в данное время и еще один раз вещь» [Там же. Р. 8]. Посредством этой интуиции жизненный момент разделяется на последовательность качественно различных вещей, состояний. Выделяемые с помощью интуиции времени природные последовательности затем «концентрируются в интеллекте, хотя и не в чувственных, но, тем не менее, воспринимаемых математических последовательностях» [Там же. Р. 81 ]. Выделение полезных систем и их представление в интеллектуальных математических системах позволяет человеку делать предсказания и принимать предупредительные меры, что придает ему новые силы в борьбе за существование. На определенной ступени познания природы используются более абстрактные и широкие математические системы, а именно «построенные с помощью математической индукции математические системы, называемые законом» [Там же. P. 84J.
Л. Брауэр останавливается на классической проблеме пространства и времени, «с тем чтобы выяснить, в какой мере могут быть признаны объективными или априорными математические системы» [Там же. Р. 94]. В этой части Л. Брауэр формулирует свои взгляды, сравнивая их с содержанием трансцендентальной эстетики «Критики чистого разума» И. Канта и взглядами Б. Рассела на
77
основания геометрии. Брауэр различает два смысла априорности: априорность в смысле существования независимо от опыта (напомним, по Канту, опыт сводится к порождению форм чувственности под воздействием «вещей в себе») и априорность в смысле необходимого условия возможности науки. Пространство как «научно существующий многомерный континуум», согласно Л. Брауэру, не зависимо от опыта и применяется к опыту a posteriori. В этом смысле геометрия, изучающая пространство, априорна. Но пространство, согласно концепции Л. Брауэра, не является ни необходимым условием опыта, ни необходимым условием возможности науки. Пространство не есть необходимое условие опыта ни в объективном (в смысле расселовского «выведени" евклидова трехмерного пространства из внешнего мира), ни в субъективном плане (в смысле изначальной интуиции пространства). Время также не может выводиться из внешнего опыта и в этом смысле оно априорно. Однако времени Л. Брауэр отводит роль априорного условия «математического рецептуирования опыта» и единственного необходимого и достаточного условия построения всей математики. Математика, согласно Брауэру, «определенно целиком не зависима от материального мира» [121. Р. 177], она есть «свободное творчество, не зависимое от опыта» [Там же. Р. 179].
Первичные математические объекты — натуральные числа — Л. Брауэр считает возможным ввести с помощью так называемой математической первоинтуиции, которая состоит в отвлечении (абстракции) от качественной стороны различных восприятий изменения. Такая абстракция своим результатом имеет «лишенный качества субстрат всех восприятий изменения» [Там же. Р. 3], представляющий их общую, абстрактную структуру. Последняя включает в себя «настоящее» (в смысле восприятия настоящего), постоянно переходящее в новое «настоящее». Однократное применение первоинтуиции математики преподносится в качестве способа введения порядковых чисел «первый» и «второй» (и соответствующих им количественных чисел). Многократное применение этой абстракции к текущему потоку восприятий порождает счетную последовательность натуральных чисел. Введенные таким путем натуральные числа Л. Брауэр считает «интуитивно ясными» [Там же. Р. 3]. Затем конструируются другие более сложные математические объекты. Ход построения математических объектов Л. Брауэр ставит под контроль интуиции, которая одна устанавливает, что допускается в качестве дозволенного и что не допускается. Брауэр исключает возможность математики, которая не строилась бы интуитивно: интуитивное усмотрение является
78
«единственным основанием математики», и «все другие попытки отыскать фундамент терпят провал» [121. Р. 77].
Интуитивно формируемая математика, согласно Брауэру, не зависима от так называемых законов логики, законов рассуждения или человеческого мышления: «Логическое построение математики, не зависимое от математической интуиции, невозможно» [Там же. Р. 180]. Область математики растет «свободно и интуитивно». Сопутствующая языку «свобода от противоречия» не является критерием математического существования, «существование в математике означает: интуитивное построение» [Там же. Р. 177]. Таковы, по Брауэру, общие философские основания науки вообще и математики в частности. Пример Кантора и Брауэра показывает, как выстраиваются философские основания научных теорий.
Философские положения, выражающие понимание социальных, общественных потребностей, ради прямого или косвенного удовлетворения которых предпринимается научное познание, понимание социальной роли теоретических результатов научного познания в жизни человека и социума, составляют социально-философские основания теории. Американский философ науки X. Лейси отмечает, что во всех сферах повседневной жизни людей «прослеживается направленность на неограниченную экспансию средств эффективного контроля над объектами» 150. С. 167]. Это значит, что социум заинтересован, в частности, в разработке научных теорий, обеспечивающих в конечном итоге эффективный контроль человека над природой и социальной средой с целью удовлетворения своих потребностей. В конечном итоге научные теории возникают из потребности изучения явлений природы и социума как объектов преобразующей деятельности человека и общества, создания искусственных орудий преобразующей деятельности, решения управленческих задач в условиях коллективных действий людей, задач координации коллективных усилий, предотвращения опасных последствий глобальной практической деятельности человечества. Последний мотив лежит в основе «экологизации» науки и образования.
К основным функциям теории относятся описание объектов (концептуальное моделирование), объяснение и предсказание фактов. Описание на эмпирическом уровне опирается на чувственный опыт и указывает на внешний вид, форму цвет, размер и другие чувственно воспринимаемые признаки. Описание на теоретическом уровне дается с помощью теоретических понятий и высказываний.
В общем плане описание на эмпирическом уровне научного познания достигается фиксацией результатов опыта (наблюдения
79
и эксперимента) с помощью научного языка [66. С. 199—200]. Так, эмпирическое описание феномена острого холецистита дается перечислением таких признаков, как острое начало после погрешности в диете, обычно сильные боли в правом подреберье, повышенная температура, напряженность мышц живота, учащенный пульс, тенденция артериального давления к снижению, желтуш-ность кожных покровов, склер и слизистых на вторые-третьи сутки, В специальных теориях формой описания является концептуальная модель объектов познания. В качестве теоретического описания в принципе может выступать любое выражение в языке теории типичных, характерных признаков объектов теоретического познания. Теоретическое описание отличается от содержания понятий тем, что не подчиняется принципу «Каждый из перечисленных признаков необходим, а вместе взятые перечисленные признаки достаточны для выделения описываемых явлений из множества всех явлений».
Описание в науке является необходимым условием объяснения и предсказания фактов. От В. Дильтея идет противопоставление объяснения как научного метода естествознания пониманию как методу психологии и наук о духе. Однако в любых отделах науки проблема объяснения связана с потребностью понимания. Понимание, прежде всего, рассматривается в контексте коммуникации, когда речь идет о понимании содержания сообщений в смысле уяснения значений и смыслов языковых выражений, входящих в сообщение источника информации. Для описания контекста языковой коммуникации полезно иметь в виду так называемый семантический треугольник:
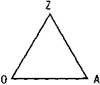
Z в треугольнике символизирует языковое выражение в составе сообщения (слово, словосочетание и даже предложение, которые называются языковыми знаками), О — объект, о котором идет речь в сообщении (вещь, предмет, свойство, отношение), А — образ объекта О в сознании человека. Если образ А объекта О представлен (в традиционной терминологии — «выражен») языковым знаком Z, то Z выступает в роли имени или обозначения объекта О
80
(является именем объекта О). Объект О является, как говорят логики, денотатом (референтом, десигнатом) языкового знака Z. Денотат О языкового знака Z обычно называют предметным значением или просто значением знака Z, тогда как образ А денотата О называется смысловым значением или просто смыслом знака Z.
Воспринятый в ходе языковой коммуникации языковой знак Z по самой сути функции именования имеет назначением «отсылать» воспринимающего знак Z человека к смыслу А и денотату О знака Z. Понимание, таким образом, означает уяснение того, с какими денотатами (из целостного поля объектов) и смыслами (из целостного поля смыслов) источник сообщения связывает входящие в сообщение языковые выражения и сообщение в целом.
Специфический оттенок термин «понимание» приобретает в научном познании, где понимание сближается с процедурой интерпретации в смысле процесса подведения готовых (или вырабатываемые но ходу дела) научных смысловых единиц, содержащихся в научных смысловых (культурных) ресурсах (контекстах) исследователя, под воспринимаемые знаки и явления [67. Ч. II, гл. 5]. Движение в этом случае идет от «готового» смысла (смысл — «данное» для воспринимающего сообщение) к объекчу познания (денотату) . Понимание в этом случае достигается с помощью принадлежащих исследователю (научному сообществу) смысловых единиц, которые «вкладываются» в воспринимаемые знаки и явления. Такое движение, естественно, предполагает ту или иную форм)' реального различения смысла и денотата, а также какую-то форму их соответствия. Поскольку смысловые единицы, содержащиеся в культурных ресурсах воспринимающего сообщение человека, выражены в его собственном языке, понимание принятого сообщения выглядит как процедура смыслового отождествления (приравнивания) языковых знаков «приемника» сообщения с языковыми знаками источника сообщения.
Научное объяснение, дающее понимание описываемых фактов, обычно связывают с использованием законов науки. В этой связи вырисовываются две возможные ситуации с объяснением и пониманием. Во-первых, в науке бывают ситуации, когда факты доступны эмпирическому описанию, а объясняющие их законы наукой еще не открыты. Так было в истории познания структуры атома. Какие-то экспериментальные данные, подчас парадоксального характера, в руках физиков были. Этот фактический материал было невозможно объяснить законами классической физики (механики), а новые законы квантовой механики еще не были сформулированы. Эмпирический материал, касающийся микро-
81
мира, был непонятен исследователям, и его следовало объяснить, обнаружив новые объективные законы. Акцент в научном объяснении как гносеологической процедуре здесь делается на поиске объясняющих законов.
Во-вторых, может быть и другая ситуация, когда факты объяснимы и понятны в контексте известных законов науки, и проблема сводится к вопросу о возможности объяснения этих фактов другими (в принципе уже известными) законами (процедура переинтерпретации, формирования новой интерпретации). Акцент в процедуре объяснения и понимания в подобной ситуации переносится на выводимость известных фактов из известных же законов пауки. В этой ситуации нет проблемы объяснения и понимания абсолютно непонятных фактов, поскольку рассматриваемые факты уже имеют объяснение и поняты на основе некоторых известных законов. Если с подобной процедурой объяснения и связано нечто непонятное, то оно касается лишь пригодности новых законов для объяснения рассматриваемых фактов. Другими словами, непонятно, можно ли дать уже объясненным и понятым на основе некоторых законов фактам новое объяснение. Эту ситуацию можно назвать переосмыслением фактов на основе новой теории. Таким образом, объяснение можно давать как непонятным, так и понятным в некотором относительном смысле фактам. По-видимому, к этому можно свести смысл слов Гейзенберга: «Наука идет вперед не только потому, что нам становятся известны и понятны новые факты, но и потому, что мы все время заново учимся тому, что может означать слово "понимание"» [25. С. 398].
Объекты объяснения (следовательно, и понимания) разнообразны. Обычно при рассмотрении объяснения говорят об объяснении отдельных фактов и явлений. Р. Карнап [41. Ч. 1, гл.1] приводит следующий пример объяснения (обыденного). Некто N оставил в своем кабинете свои часы и ушел из кабинета. Вернувшись, он не обнаружил своих часов в кабинете. Его заинтересовал вопрос о том, как объяснить отсутствие в кабинете оставленных им часов. Таким образом, перед ним типичная проблема объяснения факта-события — исчезновения часов из кабинета. Объяснение было найдено, когда нашелся свидетель, сообщивший, что в кабинет заходил К., который и унес собой часы. Здесь один факт («Часы N исчезли из кабинета»), согласно Р. Карнапу, находит объяснение в другом факте («К. унес часы N из кабинета»). Такое объяснение не является теоретическим: теория не задействована в объяснении. Карнап считает, что приведенное обыденное объяснение может быть переведено в теоретическое объяснение, если
82
мы привлечем к объяснению некоторые теоретические положения, например законы науки. В данном случае можно апеллировать к теоретическому закону, выраженному чисто универсальным высказыванием: «Всякий раз, когда нечто перемещается из одной точки (области) пространства в другую, это нечто больше не находится в исходной точке (области) пространства».
Научное объяснение отдельного индивидуального факта указывает на то, что объясняемый факт связан с другим фактом (другими фактами), по меньшей мере, посредством одного закона как объективной, всеобщей и необходимой связи (динамического или статистического типа). Таким образом, гносеологический смысл теоретического объяснения состоит в возведении индивидуального, единичного факта на уровень всеобщности и необходимости. При теоретическом объяснении исчезновения часов из кабинета единичный факт подведен под форму всеобщего закона, что и сделало понятным единичный факт исчезновения часов. Симптоматичны в этом отношении слова Ч. Дарвина о том, что он стремился к пониманию путем выяснения законов, лежащих в основе изучаемых явлений.
Апелляцию к законам науки при объяснении явлений, фактов нередко трактуют как познание сущности (устойчивого, сохраняющегося, необходимого момента) объясняемых фактов, явлений. Сторонники феноменалистской философии науки утверждают (см. подробнее [65. С. 52[), что научные законы никакой сущности не раскрывают, поскольку объяснение частного явления путем сведения его к общему закону состоит просто в том, что явление, происходящее теперь, объявляется примером, экземплификацией того, что происходит всегда. Такая процедура не нацелена на раскрытие сущности объясняемого явления. С точки зрения материалистической гносеологии, категории сущности и закона являются однопо-рядковыми и выражают углубление познания явлений. В рамках этой гносеологии объяснение связывается с познанием сущности.
Для выражения структуры теоретического объяснения фактов Р. Карнап предложил следующую общую схему:
У(х)(Р(х) => G { x )) («Если всякий объект х характеризуется признаком Р, то всякий объект охарактеризуется и признаком G»);
Р(а) («Данный конкретный объект а характеризуется признаком Р>);
G { x ) («Данный конкретный объект а характеризуется признаком G»).
Первое утверждение представляет универсальный закон, который применяется к любому объекту класса (типа) х. Смысл
83
этой посылки следующий: универсальная характеристика G( x) объектов класса х верна всегда, когда будет верной универсальная характеристика Р(х) объектов того же класса х. Вторая посылка Р(а) приведенного умозаключения является единичным высказыванием, фиксирующим принадлежность объекта а к объектам класса х, характеризующимся свойством Р. Это высказывание является констатацией результатов познания, установившего факт принадлежности единичному объекту а свойства Р. Утверждение G( a), фигурирующее в качестве вывода, еще до процедуры объяснения получено в качестве чувственно-эмпирической констатации факта принадлежности единичному объекту а свойства G. Именно зафиксированный в заключении факт нуждается в объяснении. Посылки умозаключения, взятые вместе, являются основанием для вывода: объект а, принадлежность которого к классу х установлена, характеризуется свойством G. Общий объяснительный смысл приведенного умозаключения можно выразить следующим образом: объект «характеризуется свойством G потому что а относится к объектам класса х, а все объекты типа х характеризуются свойством G. Факт имеет место потому, что действует некоторый универсальный закон.
Научному объяснению подлежат не только отдельные факты, но и множества фактов. Раскрывая смысл понимания, сопровождающего такого рода объяснения, В. Гейзенберг пишет: «Понять природу — значит заглянуть в ее внутренние взаимосвязи, точно знать, что мы вникли в ее скрытые механизмы. Такое знание не дается осмыслением одного отдельного явления или одной отдельной группы явлений, даже когда мы открыли в них определенный порядок; оно достигается лишь тогда, когда мы устанавливаем широкие взаимосвязи, сводим к одному простому корню огромное множество опытных фактов» [25. С. 310]. Из слов Гейзенберга видно, что понимание может состоять и в раскрытии внутренней взаимосвязи элементов системы, в раскрытии скрытых механизмов взаимосвязи и функционирования. Понимание в этом случае предполагает владение представлениями, концепциями, с помощью которых мы можем рассматривать огромное множество различных явлений в их целостной связи. Гейзенберг указывает: галилеевские законы падения, движение Луны вокруг Земли, движение планет вокруг Солнца, колебания маятника, траектория брошенного камня —все эти явления могли быть выведены из основной предпосылки ньютоновской механики —уравнения: массах ускорение = сила — в совокупности с законом притяжения. Таким образом, математическое уравнение, отображающее эти явления, было абстрактным ключом
84
к пониманию весьма широкой области природы. Знаменательными являются слова Гейзенберга, что объяснение состоит в обнаружении единства внешне разнообразных фактов и явлений. Как и в случае объяснения отдельных фактов, общий смысл понимания внутренних взаимосвязей состоит в рассмотрении конкретной, кажущейся запутанной ситуации в качестве частного следствия чего-то более общего. Сведение пестрого многообразия явлений к общему и простому, «многого» — к «единому» лежит в основе понимания.
Законы логики и чистой математики благодаря самой их природе не могут быть использованы в качестве основы для научного объяснения, потому что они ничего не говорят нам о том, что отличало бы действительный мир от некоторого другого возможного мира. Когда требуется объяснение факта, необходимо использовать конкретные научные законы, прежде всего эмпирические. Они не обладают достоверностью логических и математических законов, но говорят нам нечто о мире.
С логической точки зрения объяснение отдельных фактов и систем состоит, как это было проиллюстрировано выше, в дедукции положения, описывающего факты. В качестве посылок дедукции берется один или несколько универсальных законов совместно с определенными единичными положениями, выражающими начальные условия. К. Поппер предложил для выражения логического смысла объяснения более простую формулу
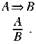
Условная посылка А=>Вутверждает, что описание В некоторого рода фактов будет верным всегда, когда будет верным описание А другого рода фактов. Описание А, фигурирующее в качестве второй посылки умозаключения, является экземплификацией описания А из первой посылки и появляется в результате чувственно-эмпирической констатации некоторого единичного факта. Описание В, фигурирующее в заключении, является экземплификацией описания В из первой посылки, удостоверенное чувственно-эмпирическим познанием. Таким образом, А во второй посылке и В в заключении являются сингулярными эмпирическими высказываниями.
Иногда против приведенной строго дедуктивной трактовки объяснения выдвигаются возражения (см. [106. С. 152—154]). В частности, утверждается, что в реальном объяснении как познавательном процессе вначале формулируется эмпирическое единич-
85
вать пониманию сути дела. Тем более что традиции западной философии науки связаны с употреблением термина «предсказание» при рассмотрении научной практики предвосхищения [40. С. 56]. Кроме того, употребление слова «предсказание» для обозначения научной практики предвосхищения предпочтительно и с чисто языковой стороны. Можно говорить о предсказательном потенциале научного знания, но нельзя образовать такой словесный оборот с использованием термина «предвидение».
Предсказательный потенциал научной теории можно считать высшей мерой ее значимости. Научное предсказание в отличие от различных «гадательных» практик опирается на использование законов науки. Логическая схема предсказания схожа со схемой объяснения:
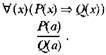
Однако смысловые акценты в схеме предсказания иные по сравнению со схемой объяснения. В обеих схемах фигурирует универсальный научный закон, выражающий связь между обобщенными описаниями Р(х) и Q _( x ) элементов некоторого класса объектов: если любой объект класса х имеет свойство Р, то любой объект класса х имеет также свойство Q . Кроме того, в обеих схемах присутствует эмпирическое высказывание, фиксирующее результат чувственно-эмпирического познания единичного объекта а из класса объектов х. Оно, как говорится, экземплифицирует фигурирующее в законе универсальное описание Р(х). Это высказывание фиксирует принадлежность объекту а из класса объектов х свойства Р. Однако фигурирующая в заключении обеих логических схем (объяснения и предсказания) эвземплификация содержащегося в законе универсального описания Q ( x ) в случае предсказания имеет иной смысл по сравнению с объяснением. Напомним, что в случае объяснения содержащаяся в выводе умозаключения эк-земплификация универсального описания Q ( x ) имеет место до объяснения как результат чувственно-эмпирической констатации некоторого положения дел, фиксируемого единичным эмпирическим высказыванием. В случае предсказания вывод умозаключения формально также является экземплификацией универсального описания 0_(х) и имеет форму сингулярного эмпирического высказывания. Однако это высказывание появилось вовсе не в результате предваряющей предсказание чувственно-эмпирической констатации описываемого положения дел, свидетельства. Оно появляется
88
впервые как заключение, вытекающее из посылок предсказательного умозаключения и предвосхищающее результаты будущей чувственно-эмпирической констатации утверждаемого положения дел («предвосхищающее опыт»). Это высказывание имеет следующий познавательный смысл: будущий опыт покажет принадлежность свойства Q объекту а из класса х. Предсказательный смысл приведенного умозаключения можно выразить следующим образом: будущий опыт должен показать принадлежность свойства Q объекту а из класса х, поскольку имеются универсальный закон \/(х)(Р{х) => Q( x)) и опытно засвидетельствованное сингулярное высказывание Р(а). Таким образом, в случае предсказания ситуация, описываемая Q( a), чувственно эмпирически еще не констатирована и предсказывается ее существование.
Из тезиса, что предсказание является предвосхищением опытно не установленных к моменту предсказания фактов, вытекает, что предсказание можно относить как к будущим (и, естественно, на момент предсказания не констатированным в опыте) явлениям, так и к уже существующим, но еще на момент предсказания не констатированным в опыте явлениям (см. [78. С. 350]). Примером предсказания будущих событий является предсказание солнечного затмения. В предсказании будущего речь идет о теоретически выраженных с помощью высказываний фактах, выходящих за пределы непосредственно данного. Однако предсказание правомерно относить и к событиям, уже существующим, по в опыте не известным (и значит, по нашему определению, фактами не являющимся). Наиболее известным примером такого рода является предсказание существования планеты Нептун. Столь же типичны предсказания, касающиеся существования полезных ископаемых в различных частях Земли.
Признавая новаторский характер идеи предсказания существующих явлений, объектов и событий, но находящихся за пределами, за границами человеческого опыта, мы считаем возможным сделать еще один шаг вперед. А именно, мы считаем возможным расширить понятие предсказания, распространив его с будущих и существующих (на момент предсказания) событий на события, существовавшие в прошлом, но уже не существующие на момент предсказания. Этот вид предсказания можно было бы назвать «ретроспективным предсказанием», поскольку он фигурирует в контексте ретроспекции. Поясним этот вид предсказания примером геолога, который на основании обнаруженных борозд на валунах у берега моря или океана и соответствующего эмпирического закона, согласно которому такие борозды оставляются на валунах
89
ледниками, делает предсказание, что некогда в прошлом данная область была покрыта ледником. Выделенный вид предсказания близок процедурам предположительного объяснения, гипотетического установления причин. Однако при должной расстановке акцентов этот вид теоретической деятельности вполне отвечает понятию предсказания.
Термин «предсказание» для всех рассмотренных познавательных ситуаций используется потому, что в каждом случае мы имеем ту же самую логическую схему и ту же ситуацию: из известного факта и известного закона выводится утверждение о существовании эмпирически еще не установленного, в опыте не зафиксированного положения вещей (и в этом смысле «будущего факта»).
При предсказании могут использоваться как динамические, так и статистические законы. В случаях использования статистических законов предсказание будет только вероятным. Метеоролог, например, имеет дело одновременно с различными статистическими законами. Он не может сказать, что завтра будет дождь, он может только сказать, что дождь очень вероятен. Эта неопределенность также характерна для предсказаний человеческого поведения. Па основе знания некоторых психологических законов статистического характера и некоторых фактов, касающихся данного лица, можно предсказать с различной степенью вероятности, как оно поведет себя в тех или иных ситуациях.
Органическим моментом предсказаний с использованием статистических (вероятностных) законов является проблематичность, гипотетичность, вероятный характер результата. Понятие вероятности обычно считается плодотворным и содержательным лишь в применении к массовым случайным событиям стабильной частоты (частотой называется отношение числа случаев, в которых данное событие наступило, к общему числу всех наблюдавшихся случаев). События, которые могут произойти или не произойти в результате произведенного опыта, называются случайными и составляют исходы опыта. События, таким образом, случайны в том смысле, что их наступление или ненаступление не определяются однозначно некоторым комплексом условий. Вероятность характеризует степень возможности появления данного события А при неограниченном числе воспроизведений комплекса условий S' и представляет собой объективную характеристику связи данного события с этим комплексом условий.
Для численной оценки вероятности того или иного события применяются два способа. Первый способ опирается на результаты наблюдения частоты наступления события в длинной серии
90
опытов. При многократном воспроизведении комплекса условий S частота осуществления данного события А остается приблизительно стабильной, близкой к определенному числу р, которое служит мерой вероятности данного события. Подчеркивается при этом, что существование вероятности не зависит ни от производимых опытов, ни от наблюдений этого события [27. С. 44; 116. С. 14; 128. S. 24].
Второй способ определения численного значения вероятности опирается на различного рода соображения симметрии, согласно которым с равным основанием может осуществляться любой из исходов данного опыта. В этом случае все исходы считаются равновероятными. Вероятность рассматриваемого события определяется как отношение числа исходов опыта, благоприятных для этого события, к общему числу исходов. При этом равноправность исходов опыта стремятся вывести из физических законов, согласно которым совершаются события. Например, при выбрасывании игральной кости, если ее грани не отличаются друг от друга физическими свойствами, влияющими на исход опыта, выпадение любых граней равновозможно, и поэтому вероятность выпадения какой-либо определенной грани равна 1/6 .
В изложенной интерпретации речь идет о вероятности как объективном свойстве реального события, объективной характеристике связи события с определенным комплексом условий. Объективность усматривается в том, что существование вероятности не зависит от наблюдения, опыта, от присутствия или отсутствия экспериментов. Такая вероятность может характеризоваться как «объективная», или «онтологическая».
Объективная интерпретация вероятности противопоставляется «субъективистскому» пониманию, которое состоит в истолковании вероятности как «меры уверенности» исследователя в наступлении какого-либо события, вытекающей из количества имеющейся у него информации [27. С. 16, 18—20]. Э. Борель, действительно, называл такую вероятность «субъективной» [16. Гл. 1] и обозначил ее через Р(А, К), имея в виду вероятность события А при наличии совокупности сведений К, которая заключена в некотором человеческом сознании. Если два человека обладают по отношению к событию А в точности одинаковой совокупностью сведений К, то значения вероятностей для этих двух людей будут одни и те же. Однако может случиться, что для одного и того же человека совокупность сведений К с течением времени видоизменится и станет К'. В этом случае вероятность также изменится, и ее надо будет записать как Р(А, К) [Там же. С. 13]. Ссылаясь на Кейнса,
91
Э. Борелъ заключает, что «вероятность не существует отвлеченно, а только по отношению к определенному человеческому мозгу, то есть относительно некоторой совокупности сведений К» [16. С. 13 ]. Борель при этом подчеркивал, что совокупность К может содержать недостаточную информацию, ошибочные сведения и т. п. Если считать вероятность объективной мерой реального события, то вышеизложенное понимание вероятности представляется субъективистским, так как объективную характеристику события ставит в зависимость от нашего знания, его полноты. Для науки, разумеется, недопустимо считать, что знание (его полнота, ошибочность и т. п.) определяет объективно существующее свойство реальных явлений. Критика подобного понимания вероятности реальных событий является условием правильного истолкования теории вероятностей как науки. Следует, однако, иметь в виду, что Э. Борель ведет речь о случаях оценки вероятности будущих событий, которые произойдут при осуществлении некоторого комплекса условий S. Однако исследователям в точности не известен комплекс S. Поэтому при подсчете вероятности они могут разойтись в мнениях, так как будут принимать в расчет различные комплексы S. Какой именно комплекс S примет исследователь для подсчета вероятности события, зависит от имеющейся у него информации К. Связь же события с комплексом условий S ot исследователя и его знаний не зависит.
Критика «субъективистского» истолкования вероятности иногда доводится до требования принципиально различать суждения следующих типов:
а) «Вероятность выпадения любой грани куба равна 1/6»;
б) «Вероятно, что любое натуральное четное число, большее
двух, может быть представлено как сумма двух простых чисел».
Указывается, что суждения типа (а) отвечают двум основным требованиям научности. Во-первых, они имеют объективный смысл, то есть отражают объективное положение вещей: вероятность р характеризует частоту наступления события А при условии многократного воспроизведения некоторого комплекса условий S. Утверждать, что при некотором комплексе условий S появление события А имеет вероятность р, «значит утверждать наличие между комплексом условий S и событием А некоторой вполне определенной, хотя и своеобразной, но от этого не менее объективной, существующей независимо от познающего субъекта, связи» [27. С. 16]. Во-вторых, суждения типа (а) являются точными (значение р является постоянным и определенным числом) отражениями характера связи события А с комплексом S.
92
Суждения типа (б) не отвечают обоим вышеуказанным требованиям: они не отражают никакой объективно-закономерной связи между каким-либо реальным событием и принципиально воспроизводимым комплексом условий S, а обозначают лишь субъективное отношение говорящего к вопросу и поэтому не могут содержать никакого объективно-значимого и точного численного значения вероятности.
Действительно, суждения типа (б) не так точны, как суждения типа (а). Бесспорно также, что в суждениях типа (б) речь идет не о вероятности как объективном свойстве реальных вещей и что они в известном смысле выражают субъективное отношение говорящего к вопросу об истинности высказываемого положения, то есть не могут интерпретироваться на основе онтологической вероятности. Но отсутствие онтологической трактовки суждений типа (б) не означает, что суждения этого тина основываются на «субъективистской» интерпретации вероятности. Кроме онтологической вероятности существует логическая, характеризующая логическую связь между посылками и заключениями индуктивного вывода (об этом речь пойдет ниже, при рассмотрении индукции как метода познания). Логическая вероятность характеризует зависимость знания, гипотез, высказываний от других знаний, гипотез, высказываний, в том числе эмпирических данных.
Вероятность как элемент суждения есть субъективный образ объективного свойства. С помощью субъективных образов в суждениях мы приписываем вероятности как объективной характеристике связи события А с комплексом условий S некоторое численное значение. Насколько точно мы это делаем, зависит, в частности, и от «чистоты» подведения реальных явлений под стандартные ситуации теории вероятностей. В данном случае речь идет о приближенной оценке объективной вероятности. Логическая вероятность, как и онтологическая, не зависит от воли и желания исследователя.
В традиционной индуктивной логике сложилось два направления исследований — обоснование общих положений, принимаемых в качестве гипотез, частными положениями и фактами (индукция как умозаключение) и исследование причинных связей. Именно во втором направлении исследований существенную роль играет понятие объективной вероятности, с помощью которой формулируется статистический закон. Последний может использоваться как для предсказания наступления следствия при заданной причине (прямая задача), так и для предсказания причины по наступлению заданного следствия («обратная индуктивная задача
93
С. Джевонса»). Смысл обратной задачи Джевонса изложен в [90. С. 262-265].
Предсказание существенно как для повседневной жизни, так и для научного познания. Большинство тривиальных действий, которые мы осуществляем в течение дня, основывается на предсказаниях. На основе знания специфических фактов и познания определенных регулярностей обеспечивается база для предсказания фактов. Предсказание является эффективным средством пополнения множества научных фактов. Уже упоминавшийся Э. Мах такое пополнение известных фактов новыми фактами путем предсказания в соответствии со своей феноменологической философией трактует как процедуру простого описания. Задачей науки он считает дополнение «в мыслях» фактов, данных лишь отчасти. Это, согласно Маху, и осуществляется через процедуру предсказания. Позиция Маха не позволяет разграничить научное предвидение событий и фактов, с одной стороны, и «гадательное» предсказание будущего так называемыми ясновидцами, основывающимися на толковании снов, наблюдении за полетом птиц, за особенностями внутренностей жертвенных животных и т. п., с другой стороны. Некоторые предсказания ясновидящих сбываются и, следовательно, также пополняют уже известные факты. Для научного познания главное — не в простом «гадательном» описании будущего. Нa-учное предвидение — это эффективное средство установления закономерного, необходимого характера взаимосвязей мира и фактов, эффективное средство распространения познанной необходимости на область еще не познанного. Правильное предсказание является средством, способствующим переходу человека к новой познавательной или практической ситуации, к постановке новых познавательных проблем, формированию новых теоретических представлений. Человек прибегает к научному предсказанию в особенности с целью эффективной подготовки себя к будущему.
Дата: 2018-12-21, просмотров: 355.