| Пол | № | Свободное время, проведенное вне дома
| ||
| Холостые | Женатые | Разведенные | ||
| Мужчины | 1 | 8 | 4 | 9 |
| 2 | 7 | 7 | 7 | |
| 3 | 9 | 6 | 5 | |
| 4 | 6 | 8 | 4 | |
| Женщины | 1 | 5 | 6 | 7 |
| 2 | 7 | 5 | 8 | |
| 3 | 4 | 3 | 6 | |
| 4 | 5 | 4 | 6 | |
Здесь возникает более сложная задача — проверить не только влияние каждого фактора (семейное положение и пол) по отдельности, но и взаимодействие этих факторов. Задача может еще более усложниться, если ввести в рассмотрение третий фактор. Например, проживание в крупном городе, где проблем развлечься вне дома, или в небольшом населенном пункте, этого, необязательно ограничивать себя только одной зависимой переменной. Возможно, более интересные результаты могут быть получены, если проверить, например, сколько денег представители каждой из выделенных групп ежемесячно тратят на развлечения вне дома.
По сути дела, ANOVA — это система методов, позволяющая решать подобные задачи в случае наличия нескольких независимых переменных (факторов) и одной зависимой. МANOVA (многомерный дисперсионный анализ) позволяет делать то же самое, но для большего числа зависимых переменных.
Математический аппарат, используемый в ANOVA и МANOVA, несложен (вычисление средних и дисперсий), но громоздок, поэтому эти методы получили своё повсеместное распространение с началом эры ЭВМ.
Вернемся к первому примеру. В очень упрощенном виде основная логика однофакторного дисперсионного анализа выглядит следующим образом.
1. Если объединить три подгруппы (холостые, женатые, разведенные), то для объединенной выборки (24 человека) можно вычислить среднее и дисперсию (общегрупповая дисперсия).
2. Аналогичным образом вычисляется среднее и дисперсия для каждой из подгрупп (внутригрупповая дисперсия).
3. Кроме этого, вычисляется дисперсия средних значений при переходе от подгруппы к подгруппе (межгрупповая дисперсия). В соответствии со свойствами дисперсии, общегрупповая дисперсия будет равна сумме внутригрупповой дисперсии и межгрупповой дисперсии.
Основой для принятия решений служит сравнение внутригрупповой и межгрупповой дисперсии.
Высокие значения внутригрупповой дисперсии (по сравнению с межгрупповой) означают, что внутригрупповые различия «перекрывают» межгрупповые различия. В этом случае нельзя утверждать, что фактор оказывает существенное влияние на полученные результаты.
Если же межгрупповая дисперсия преобладает над внутригрупповой, межгрупповые различия «перекрывают» внутригрупповые и можно говорить о наличии существенных различий между имеющимися подгруппами результатов. Фактор оказывает существенное влияние на полученные результаты.
В случае введения еще одного фактора (например, пола участников опроса) появляется еще одно слагаемое дисперсии, обусловленное взаимодействием факторов (например, семейным положением и полом). В принципе, при использовании специальных компьютерных программ для ANOVA и МANOVA количество вовлеченных в дисперсионный анализ факторов и зависимых переменных может быть довольно большим. Но уже при наличии трех факторов (семейное положение, пол, местожительства) основные сложности возникают при интерпретации результатов дисперсионного анализа.
ВКЛЮЧАЕМ КОМПЬЮТЕР...
Создадим две переменные: «семейный статус» (status) и «свободное время, проводимое вне дома» (time). Для первой переменной используем следующие обозначения: 1 - Одиночка; 2 — Женат/Замужем; 3 — Разведен/Разведена. На рис. 1.22-1.24 показаны последовательность действий для решения задачи однофакторного дисперсионного анализа (One-Way ANOVA) и полученный результат.

Рис. 1.22. Выбор требуемой статистической процедуры



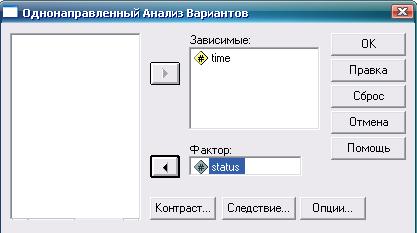
Рис. 1.23. Необходимые для однофакторного дисперсионного анализа действия
и настройки7
7 Программа SPSS предоставляет большое число возможностей для дисперсионного анализа, рассматривать которые у нас нет возможности.
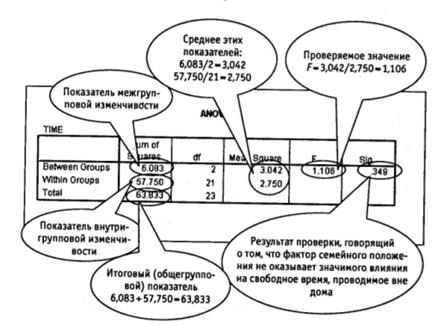
Рис. 1.24. Результат однофакторного дисперсионного анализа
Дата: 2018-12-21, просмотров: 825.