Во многих случаях для анализа имеющихся результатов используется их графическое представление.

Так, на основе таблицы 1.2 можно построить график распределения частот. Если по горизонтали (ось X) отложить значения возраста, а по вертикали (ось Y) — частоту каждого значения (сколько раз оно встречается), то можно получить либо гистограмму распределения частот, либо полигон распределения частот.

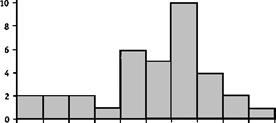
В первом случае распределение частот изображается в виде набора столби­ков, середина основания каждого из которых совпадает со значением возраста, а высота равна значению частоты для этого возраста (рис. 1.4).

6 7 8 9 10 11 12 13 14 15

Рис. 1.4. Столбиковая диаграмма (гистограмма)

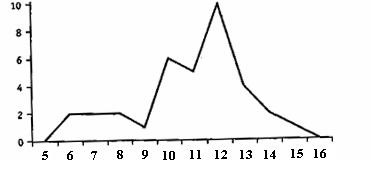
Рис. 1.5. Полигон распределения частот

Во втором случае значения частот изображаются точками, расположенными на соответствующей высоте над значениями возраста. Затем эти точки соеди­няют друг с другом отрезками прямых линий. Получившаяся «горная гряда» называется полигоном распределения частот (рис. 1.5).

Если вернуться к уже рассмотренным нами мерам центральной тенденции и мерам изменчивости, то моде будет соответствовать самое «высокое» значе­ние возраста (можно видеть, что это 12 лет). Медиана - это то значение которое делит площадь геометрической фигуры, образованной, например, гистограм­мой, пополам. А среднее - это то значение, сумма отклонений от которого влево и вправо будет равна нулю (рис. 1.6).

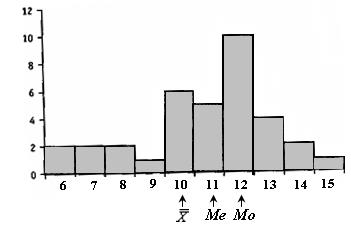
Рис. 1.6. Мода, медиана и среднее

Если экспериментальных данных очень много, то в подавляющем числе случаев распределение частот начинает приближаться к виду симметричной кривой, похожей на колокол. На рис. 1.7 приведено распределение возраста участников одного из всеизраильских исследований на тему «Молодежь и наркотики», проведенного в начале 2000-х гг. центром RADAR. В исследовании приняло участие 1235 человек в возрасте от 12 до 21 года.

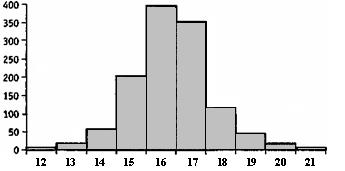
       Рис. 1.7. Распределение возраста участников исследования

В математической статистике доказывается, что по мере увеличения числа данных (в идеале — до бесконечности) такого рода распределения приближа­ются к виду, который называется кривой нормального распределения, или кривой Гаусса (по имени немецкого математика Карла Гаусса (1777—1855), который в начале XIX в. исследовал свойства такого распределения). Вид кри­вой нормального распределения показан на рис. 1.8. Оно получено на основе данных того исследования, о котором шла речь (число участников 1235). В рис. 1.8 использованы значения относительных частот, получаемых делени­ем каждой частоты на общее количество значений.

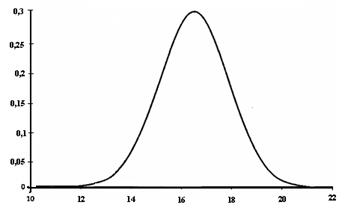
Рис. 1.8. Кривая нормального распределения

Нормальное распределение обладает рядом свойств.
Во-первых, для него все три меры центральной тенденции: мода, медиан
и среднее — совпадают друг с другом: Мо =Ме = . Из этого факта следует симметричный характер кривой нормального распределения. Поэтому в большинстве статистических таблиц для этого распределения приводятся сведения, относящиеся только к одной из его частей (чаще всего правой).  

Во-вторых, несмотря на то, что теоретически нормальное распределение простирается вдоль оси  от минус бесконечности (- ∞) до плюс бесконечности (+∞), на практике ограничиваются диапазоном ( ±3σ), где σ — стандартное отклонение. В этих пределах лежит 99,74% площади под кривой нормального распределения², что вполне достаточно для решения большинства задач³.

² «Хвосты» нормального распределения, в которых расположено 0,26% площади (по 0,13% с каждой стороны), играют важную роль при проверке статистических гипотез.

³ Выбор диапазона ± 3σ не носит принципиального характера и сделан из практических сооб­ражений. В ряде случаев рассматривается диапазон ±4 σ, в пределах которого лежит 99,997% площади под кривой нормального распределения.

Например, для нормального распределения, изображенного на рис. 1.5, 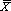= 16,5 лет, σ = 1,5. Рассмотрим какое-либо значение возраста (обозначим его как Х _i), не равное среднему. Например, Х _i = 18 лет. Введем в рассмотрение величину z, которая будет вычисляться по следующей формуле:

Нетрудно видеть, что значение z показывает, насколько далеко от среднего (слева или справа от него) расположено какое-либо конкретное значение возраста. Если возраст меньше среднего (отклонение влево), z отрицательно. Если возраст больше среднего (отклонение вправо), то положительно. Если возраст равен среднему, z равно нулю.

Как мы уже знаем, 99,74% площади под кривой нормального распределения лежит в пределах ( 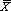±3σ). Поэтому когда речь заходит о максимальном откло­нении от среднего, то на практике обычно ограничиваются значением, равным ±3σ. Иначе говоря, если участники исследования «Молодежь и наркотики» имели среднее значение возраста  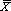= 16,5 и стандартное отклонение σ= 1,5, то можно сказать, что 99,74% всех участников имели возраст не меньше чем (16,5-3x1,5) = 12 лет, и не больше чем (16,5+ 3x1,5)=21 год.

Найдем значение z  для этих значений.

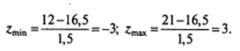
Если мы возьмем любое другое нормальное распределение с известными 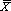и σ (например, распределение значений уровня интеллекта IQ), то получим аналогичный результат. Используемые на практике максимальные отклонения от среднего значения IQ влево и вправо от него, выраженные через значение z, также будут лежать в пределах от z_min  = -3 до z_max = +3.

Это очень важный вывод, поскольку он позволяет не учитывать природу тех конкретных данных, на основе которых было получено нормальное рас­пределение. Вместо конкретных значений, например, возраста, IQ, заработ­ной платы, тревожности и др., откладываемых по шкале X, можно перейти к единицам г-шкалы, имеющей диапазон значений от -3 до +3 (реже от -4 до + 4) для любого нормального распределения. Тем самым все нормальные распределения как бы приводятся к «общему знаменателю», в роли которого выступает z -шкала, и появляется возможность сравнивать различные распре­деления между собой, независимо от того, на основе каких значений они были получены.

Кроме этого, любое нормальное распределение всегда можно преобразовать к виду, называемому единичным нормальным распределением, при котором среднее 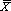=0 и стандартное отклонение σ= 1 (рис. 1.9).

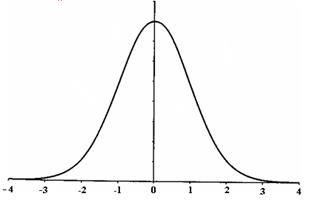
Рис. 1.9. Единичное нормальное распределение ( 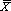=0 и σ= 1)

Это преобразование позволяет заменить большинство вычислений, связан­ных с использованием нормального распределения, работой со специальными статистическими таблицами, где приведены все относящиеся к такому распределению значения и результаты. Чаще всего используется таблица стандартного нормального z-распределения (для случая 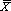=0 и σ =1).

В-третьих, долю площади под кривой нормального распределения, ограниченную одним или двумя значениями z, можно понимать как вероятность того, что нормально распределенные результаты будут лежать в определенном диапазоне своих значений.

Чтобы понять, о чем идет речь, рассмотрим пример.

Лена — очень умная девушка. Она изучает психологию, пользуется популярностью у молодых людей, но имеет высокие требования к интеллектуальное уровню тех парней, которые не прочь завести с ней дружбу. Она считает, что ее избранника IQ должен быть не ниже 130. В окружении Лены постоянно крутятся 10 парней. Есть ли у нее шанс встретить среди них человека с IQ≥130?

Как будущий психолог, Лена должна знать, что значения IQ распределен по нормальному закону таким образом, что среднее значение 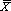= 100, а стандартное отклонение σ= 15 (рис. 1.10).

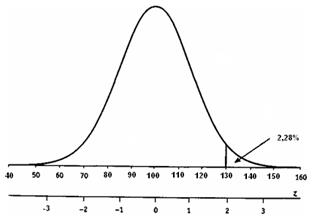
Рис. 1.10. Кривая нормального распределения для значений IQ ( 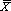= 100, σ = 15)

Для нахождения вероятности встретить парня с IQ≥130 необходимо опре­делить, какую долю площади под кривой нормального распределения отсекает это значение.

 Данная задача решается в два этапа. Во-первых, перейдем от шкалы IQ к z-шкале. Для этого по уже известной формуле определим значение z для 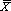= 100и σ= 15 (рис. 1.10).

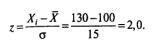
Во-вторых, в таблице z-распределения (Приложение 2, таблица 1) для каж­дого значения z в диапазоне от 0 до +4 приведено значение соответствующей площади под кривой нормального рас­пределения, лежащей правее данного значения z⁴.

⁴В таблице приведены значения только для z≥0. При работе с отрицательными значениями z используется тот факт, что кривая нормального распределения симметрична относительно z =0. Этим значением площадь под кривой нормального распределения, равная 1 (или 100%), делится на две равные части. При работе с таблицей необходимо ясное понимание того, с какой областью кривой нормального распределения мы имеем дело: лежащей левее z, правее z или между двумя значениями z₁ и z₂. Существует несколько модификаций подобной таблицы. В большинстве случаев в ней приводятся сведения для значений z от 0 до 4 или от 0 до 3.

Эта площадь понимается как вероят­ность встретить в нормальном распреде­лении результат больший или меньший какого-либо определенного значения.

Находим из таблицы, что значению z =2,0 соответствует вероятность p =0,0228. Это означает, что от площади под кривой нормального распределения отсекается 2,28%, лежащих правее z=2,0 (рис. 1.7). Но это же означает, что вероятность встретить парня с IQ≥130 рав­на 0,0228.

При наличии десяти парней вероятность, что хотя бы у одного из них будет уровень интеллекта не ниже требуемого, возрастает до 0,228, что явно недо­статочно. Лена может пойти двумя путями. Во-первых, расширить круг обще­ния с молодыми людьми и довести его до (40-45) человек, но это может повре­дить ее репутации. Во-вторых, снизить планку предъявляемых требований. Если остановиться на IQ≥120, то получим z = 1,33 и вероятность р=0,0918. В этом случае вполне возможно, что среди десятерых парней найдется один с требуемым уровнем IQ.

ВКЛЮЧАЕМ КОМПЬЮТЕР...

Для построения гистограммы используем введенную выше переменную «Возраст» (аgе). Дальнейшая последовательность действий и получаемый результат показаны на рис. 1.11-1.13.

Полученная гистограмма несколько отличается от гистограммы, приведенной на рис. 1 .4, поскольку есть отличия в масштабе по горизонтали. Одновременно с гис­тограммой приводятся среднее значение и стандартное отклонение для тех данных, на основе которых она была получена.

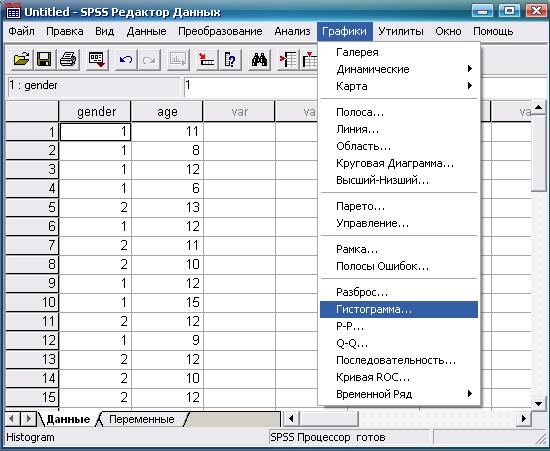
Рис. 1.11. Выбор требуемой статистической процедуры

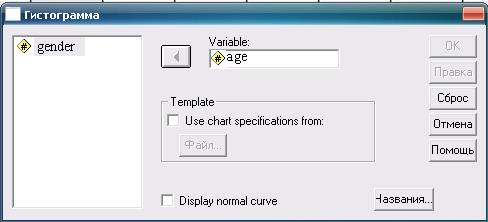
Рис. 1.12. Необходимые для построения гистограммы действия и настройки

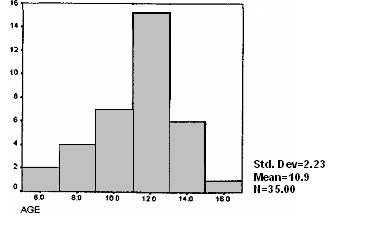
Рис. 1.13. Гистограмма: результат