Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

А. Д. РЕЗНИК

КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ,

НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ

ПРЕДИСЛОВИЕ

В свое время я был весьма обескуражен тем, с каким упорством студенты-гуманитарии избегали всего, что было связано с математической статистикой. К сожалению, к моменту окончания университета от курса статистики в памя­ти многих студентов остаются лишь разрозненные сведения и уверенность в том, что лучше с нею не связываться.

Я не собираюсь в этом никого разубеждать. В самом деле, те статистические методы, которые знакомы большинству из нас, требуют для своего корректно­го применения десятков (а лучше сотен) испытуемых, громоздких многоэтаж­ных вычислений, и, что самое главное, они не дают каких-либо гарантий в получении желаемого результата. Как следствие, использование статистики становится для многих студентов и специалистов непозволительной роскошью: потратить несколько месяцев на сбор, обработку и анализ данных, чтобы в результате не получить ожидаемых результатов.

Это тем более обидно, поскольку вот уже не один десяток лет существуют и широко используются специалистами методы так называемой непараметриче­ской статистики, позволяющие получать обоснованные статистические выво­ды при наличии крайне небольшого числа испытуемых. Зачастую для исполь­зования некоторых из этих методов достаточно выборки в 7—8 человек, что превращает непараметрическую статистику в незаменимый инструмент там, где сложно говорить о больших выборках, массовых опросах или обследовани­ях и т. п.

Другой привлекательной стороной непараметрических методов статистики является простота процесса математической обработки результатов. В ряде случаев необходимые вычисления можно сделать в уме, не прибегая ни к каль­кулятору, ни тем более к помощи компьютера.

Описанию и показу возможностей таких методов посвящена данная книга. Ее основная задача — познакомить тех, кто «не дружит со статистикой», с эти­ми методами и пробудить у них желание их использовать в своей повседневной деятельности. Содержание книги в первую очередь ориентировано на специа­листов и студентов социального и гуманитарного профиля (психологи, соци­альные работники, консультанты, педагоги, журналисты и др.).

Книга вряд ли может использоваться в качестве серьезного учебника по непараметрической статистике. Она скорее представляет собой пособие для пользователя, не имеющего серьезной математико-статистической подготовки, но желающего (или вынужденного в силу обстоятельств) использовать стати­стические методы в своей деятельности. Несмотря на то, что описание приво­димых в книге методов дано по возможности подробно и корректно, при воз­никновении противоречий между научностью и доступностью изложения выбор делался в пользу доступности (и, возможно, в ущерб научности).

Чтение книги не требует специальных знаний из области математики или статистики. В первой главе приведены минимальные сведения из математической статистики, необходимые для понимания того, о чем пойдет речь дальше.

В ряде случаев желающих использовать непараметрическую статистику отпугивает обилие здесь непривычных статистических таблиц. Однако на прак­тике выясняется, что при решении многих задач достаточно всего двух хорошо известных таблиц: таблицы z-распределения и таблицы критических значений для распределения χ². Эти и другие статистические таблицы, необходимые для рассмотрения описанных в книге методов, приведены в приложении.

При описании непараметрических методов статистики в книге использует­ся типичный в англоязычной литературе термин «тест» вместо более привыч­ного для русскоязычного читателя термина «критерий».

Приводимые в книге примеры частично базируются на результатах иссле­дований, проводимых исследовательским центром RADAR (Regional Alcohol and Drug Abuse Recourse Center) Университета Бен Гурион в Негеве, частично взяты из опыта реальной деятельности психологов, консультантов и социаль­ных работников и частично носят гипотетический характер. Одно из назначе­ний приводимых в книге примеров — показать, что необязательно быть, допустим, психологом-исследователем, чтобы испытывать потребность в ста­тистических методах. Им может найтись место не только в деятельности мно­гих специалистов, но и в обыденной жизни.

Отличительной особенностью данной книги является то, что все рассмот­ренные в ней примеры сопровождаются описанием соответствующих процедур для программы SPSS.

Программу SPSS использует в своей деятельности все большее число спе­циалистов различного профиля. Однако опыт консультирования по вопросам статистики показал, что знание этой программы не избавляет от проблем. Овладение данной программой зачастую происходит по принципу «Нажми на кнопку — получишь результат». Формально правильное выполнение всех опе­раций в программе SPSS часто сопровождается трудностями в понимании и интерпретации получаемых результатов. Поэтому каждый из приводимых в книге примеров рассматривается дважды: первый раз для вычислений вручную и второй раз для программы SPSS с необходимыми пояснениями. Это особен­но важно, поскольку программа SPSS выявила «подводные камни» ряда непа­раметрических методов, которые до этого применялись исключительно вручную: использование упрощенных алгоритмов вычислений, игнорирование ряда

особенностей в экспериментальных данных (например, наличие в них совпа­дающих или повторяющихся результатов), ограниченные возможности стати­стических таблиц и др. Как следствие, результаты, получаемые при вычисле­ниях вручную, могут не совпадать с результатами, выдаваемыми программой SPSS. В книге рассматриваются подобные случаи с описанием тех более стро­гих статистических алгоритмов, которые используются в программе SPSS при работе с непараметрическими методами.

Разумеется, все, связанное с SPSS, не может служить заменой более серьез­ным пособиям по использованию данной программы. Тем более что даже для рассматриваемых примеров за рамками книги осталось описание многих ее возможностей.

Книгу можно читать как «слева направо», так и «справа налево». В первом случае речь идет о тех, кто и испытывает потребность в статистике и собирается в дальнейшем перейти к программе SPSS. Во втором случае — о тех, кто освоил программу на уровне «кнопочного интерфейса», но не представляет, что про­исходит в ее «недрах» и что стоит за выдаваемыми программой результатами.

Я надеюсь, что книга привлечет внимание специалистов, студентов и пре­подавателей социального и гуманитарного профиля. Надеюсь, что она также будет полезна всем, желающим получить в свои руки достаточно простой и качественный инструмент статистического анализа данных.

Желающие самостоятельно попрактиковаться в использовании программы SPSS могут получить файл, содержащий все рассмотренные в книге примеры, обратившись по адресу reznikal @ bgu . ac . il . Буду рад получить по этому же ад­ресу ваши предложения, замечания и отзывы.

Доктор (PhD) Александр Резник,

Университет Бен-Гурион в Негеве, Израиль

 

 

 

 

 

 

Возраст начала курения

Респон­дент	Пол	Возраст начала курения	Респон­дент	Пол	Возраст начала ку­рения	Респон­дент	Пол	Возраст начала курения
1	М	11	13	Ж	12	25	Ж	13
2	М	8	14	Ж	10	26	Ж	11
3	М	12	15	Ж	12	27	М	13
4	М	6	16	М	12	28	М	7
5	Ж	13	17	Ж	14	29	М	10
6	М	12	18	М	7	30	Ж	6
7	Ж	11	19	М	10	31	М	12
8	Ж	10	20	М	14	32	М	11
9	М	12	21	М	10	33	М	13
10	М	15	22	М	8	34	Ж	12
11	Ж	12	23	Ж	11	35	М	10
12	М	9	24	М	12

 

В статистике для описания подобных данных обычно используют:

¤ меры центральной тенденции (мода, медиана, среднее);

¤ меры изменчивости (дисперсия и стандартное отклонение).

 

Модой (Мо) называется наиболее часто встречающееся значение среди имеющихся. Для того чтобы разобраться с модой, построим дополнительную таблицу. Поместим в нее значения возраста от минимального (6 лет) до мак­симального (15 лет), и укажем, сколько раз встречается то или иное значение возраста (табл. 1.2).

Таблица 1.2

Вычисление медианы

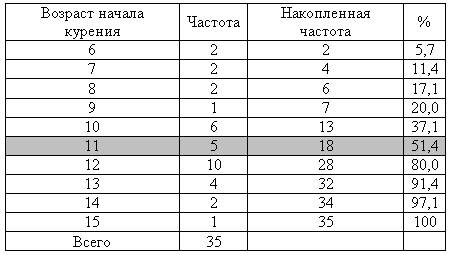
Попытаемся понять смысл полученного в последней графе результата. При переходе от шеренги «10 лет» к шеренге «11 лет» за плечами остается 37,1% всех результатов. А при переходе от шеренги «11 лет» к шеренге «12 лет» за плечами уже 51,4%. Медиана — это та точка, которая делит все данные в отно­шении 50:50. Очевидно, требуемая точка где-то внутри шеренги «11 лет». То есть Ме = 11.

На этом можно остановиться, хотя обычно для вычисления медианы используются более сложные вычисления. 

Наиболее популярной мерой центральной тенденции является среднее ( ).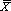

Для нахождения среднего используется простая формула, смысл которой в том, чтобы сложить все значения (в нашем случае значения возраста начала курения) и разделить полученный результат на число значений (в нашем слу­чае 35).

Дальше можно идти двумя путями.

Во-первых, начать непосредственно складывать все 35 значений возраста из первой таблицы.

Во-вторых, догадаться, что если некоторые значения возраста встречаются несколько раз, то можно воспользоваться данными из таблицы 1.2 и перейти от сложения повторяющихся значений к умножению этих значений на число повторов (например, возраст 13 лет встречается в первой таблице четыре раза, то вместо 13 + 13 + 13+13 записать 13x4). Тогда:

Меры центральной тенденции показывают, вокруг каких значений группи­руется большинство экспериментальных данных. Обычно в качестве «центра» такого группирования рассматривается среднее ( ).

Меры изменчивости говорят о том, в какой степени полученные результаты отклоняются от «центра группирования», что чаще всего приводит к опреде­лению меры отклонения экспериментальных данных от среднего.

В принципе, в качестве меры изменчивости можно было бы использовать среднее значение отклонений текущих значений от среднего. Для этого необ­ходимо определить, насколько каждое значение возраста отклоняется в большую или меньшую сторону от 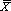= 10,89, затем сложить все результаты и разделить на число значений. К сожалению, этот путь невозможен, поскольку, как пра­вило, отклонения от среднего в большую сторону (со знаком «+») и в меньшую сторону (со знаком «-») компенсируют друг друга и в сумме дают ноль.

Для решения этой проблемы лучше использовать не отклонение от средне­го, а квадрат этого отклонения, потому что такая процедура позволяет избавиться от влияния знака. Вначале делается та же операция - определяется насколько каждое значение возраста отклоняется в большую или меньшую сторону от 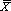= 10,89. Затем каждый из полученных результатов возводится в квадрат, все складывается и делится на число значений. Получаемая таким образом мера изменчивости называется дисперсией.

Еще раз вернемся к таблице 1.2 и дополним ее двумя графами, необходи­мыми для вычисления дисперсии. Получим таблицу 1.4.

Таблица 1.4

Вычисление дисперсии

 

Возраст начала курения   Частота   (Возраст-Среднее)   (Возраст-Среднее)²   (Частота)x(Возраст-Среднее)²   6   2   -4,89   23,91   47,82   7   2   -3,89   15,13   30,26   8   2   -2,89   8,35   16,70   9   1   -1,89   3,57   3,57   10   6   -0,89   0,79   4,74   11   5   0,11   0,01   0,05   12   10   1,11   1,23   12,30   13   4   2,П   4,45   17,80   14   2   3,11   9,67   19,34   15   1   4,11   16,89   16,89   Всего   35           ∑=169,47  

 

На практике по ряду причин технического характера, которые мы здесь не обсуждаем, для вычисления дисперсии используется другая формула, незначительно отличающаяся от предыдущей:

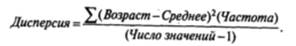
Подставим в эту формулу необходимые значения из таблицы 1.4:

К сожалению, дисперсия оказывается не очень удобным показателем меры изменчивости. Наличие в формуле квадрата меняет размерность входящих в нее величин. Например, если мы хотим определить меру изменчивости роста для группы людей, то в формуле для дисперсии будет использоваться значение (Рост — Среднее)². Размерность этого значения см². Но см² — это уже размер­ность площади, а не длины. То есть среднее значение роста будет измерено в единицах длины, а отклонение от среднего — в единицах площади.

Для решения возникшей проблемы вместо значения дисперсии использу­ется квадратный корень из нее. Полученное таким образом новое значение называется стандартным отклонением и является наиболее популярной мерой изменчивости. Стандартное отклонение часто обозначается как σ (сигма):

 

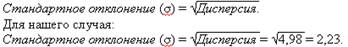
ВКЛЮЧАЕМ КОМПЬЮТЕР И ЗАПУСКАЕМ ПРОГРАММУ SPSS¹

¹ Мы предполагаем, что читатель имеет определенный опыт работы с этой программой. Поэтому операции по вводу данных, их кодировке и др. не рассматриваются.

После ввода данных о поле респондентов (переменная «Sех» с обозначением «1» для мальчиков и «2» для девочек) и возрасте начала курения (переменная «аgе» присту­паем к их обработке. Очередность действий и конечный результат показаны на рис. 1.1-1.3.

 

 

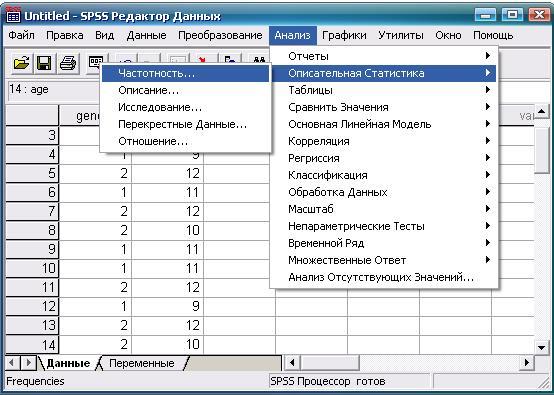
Рис. 1.1. Выбор требуемой статистической процедуры

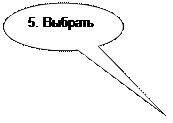
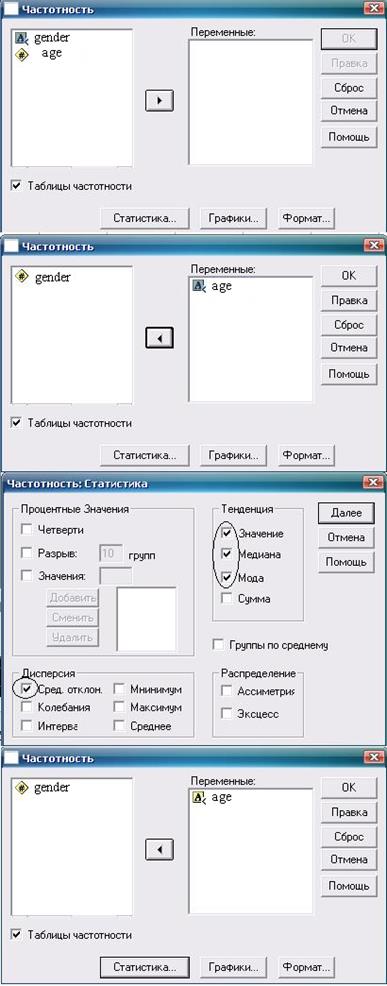
Рис. 1.2. Необходимые для обработки данных действия и настройки

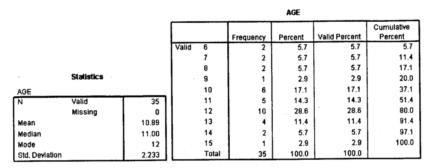
Рис. 1.3. Результат обработки

КТО БОЛЕЕ КОМПАНЕЙСКИЙ,

ПОЛНЕЮТ ЛИ ОТ СЧАСТЬЯ,

МОЛОДЕЖЬ И НАРКОТИКИ,

ИЛИ ШКАЛА НАИМЕНОВАНИЙ

 ² Быт. 2,20.

Использование шкалы наименований позволяет наделять объекты или их свойства (признаки) именами. Телефонные и автомобильные номера, различ­ные цветные фигурки на шкафчиках в детском саду и т. п. — это примеры имен, которыми мы наделяем различные объекты. При этом неважно, что будет использовать­ся в качестве имени — цифры, буквенные сочетания, условные обозначения и т. п. Основное требование здесь — не присваи­вать одно и то же имя двум разным объектам (или объектам с различными свойствами). В то же время если мы имеем дело с одина­ковыми объектами или объектами, обладаю­щими совпадающими свойствами, то они должны в шкале наименований получать одинаковые имена. Например, если выбор­ка состоит из мужчин и женщин, то можно всем мужчинам присвоить «имя» 1, а всем женщинам — «имя» 2 (или любое другое, не совпадающее с первым). Если нас интересует семейное положение, то можно всем женатым присвоить «имя» 1, холостым — «имя» 2, разведенным — «имя» 3. Количество используемых имен должно быть не меньше числа типов объектов или их свойств. Например, трех «имен» для обозначения семейного положения может оказаться недостаточно в случае наличия в выборке вдов/вдовцов. Для их обозначения потребуется дополнительное «имя».

Несмотря на то, что шкала наименований образует «низший» уровень изме­рения, ее использование является необходимым этапом при использовании статистических методов. Переход к шкалам более высокого порядка зачастую оказывается невозможен, если не решен вопрос о том, к каким объектам будут относиться получаемые данные: чтобы они были данными о чем-то, объекты должны иметь имена.

Выше отмечалось, что с каждой из шкал связан определенный набор допус­тимых математико-статистических операций. Поскольку в шкале наименова­ний числа — не более чем ярлыки, «наклеиваемые» на объекты, с этими чис­лами нельзя производить никаких действий. Их нельзя складывать или вычитать, делить или умножать. Возможен подсчет числа объектов с одинако­выми именами (например, число мужчин и женщин в выборке) или с одина­ковыми свойствами (например, уроженцы Израиля и иммигранты).

Таблица 2.2

Значения и ранги IQ детей

IQ детей	Ранг	IQ детей	Ранг
90	2	105	12
90	2	105	12
90	2	105	12
95	5	110	15
95	5	110	15
95	5	110	15
100	8,5	115	17,5
100	8,5	115	17,5
100	8,5	120	19
100	8,5	125	20

Вернемся к исходной таблице 1.5 и заменим в ней значения IQ для родителей и детей соответствующими рангами. Получим таблицу 2.5, в которой вместо значений IQ приведены ранги этих значений.

Таблица 2.5

Ранги IQ родителей и детей

Семья	Ранг IQ родителей	Ранг IQ детей	Семья	Ранг IQ родителей	Ранг 10 де-
1	2	8,5	11	11	15
2	2	2	12	11	8,5
3	2	5	13	13	17,5
4	5	2	14	15	12
5	5	5	15	15	8,5
6	5	8,5	16	15	17,5
7	8	12	17	17,5	15
8	8	2	18	17,5	20
9	8	5	19	19,5	19
10	11	12	20	19,5	15

Процедура ранжирования лежит в основе многих непараметрических методов статистики, поэтому желательно владеть навыками ранжирования в совершенстве.

Многие из непараметрических методов чувствительны к наличию связанных рангов. Связанные ранги могут существенно повлиять на получаемые резуль­таты статистического анализа. Для их учета во многие расчетные формулы приходится вносить различные корректирующие поправки⁵.

⁵ К сожалению, авторы многих учебных пособий по статистике и математическим методам в психологии обходят стороной вопрос связанных рангов. О существовании данной проблемы либо не упоминается, либо наличие связанных рангов в приводимых примерах игнорируется и вычисления проводятся по нескорректированным формулам.

 

2.4. «451° ПО ФАРЕНГЕЙТУ»⁶,

ФОРД», «ФИАТ», «ТОЙОТА»,

ИЛИ ТЕСТ х²ДЛЯ ЕДИНСТВЕННОЙ ВЫБОРКИ

Покупка машины — важный этап в жизни каждой семьи. По улицам изра­ильских городов бегает несколько десятков марок автомобилей на любой вкус, но если присмотреться, то создается впечатление, что некоторые марки встре­чаются чаще других. Для проверки этого предположения Анна и Даниил, со­бравшиеся обзавестись автомобилем, решили проверить, какие машины чаще всего встречаются на улицах их города. При этом они договорились фиксиро­вать не конкретные марки машин, а то, откуда машина «родом», — Америка (США), Европа, Юго-Восточная Азия (Япония и Южная Корея) или другое (Россия, Индия, Китай и др.). Случайным образом было проверено 80 машин, которые распределились в зависимости от места производства следующим образом (табл .3.1).

Таблица 3.1

По странам-производителям

Место выпуска	Америка	Европа	Азия	Другое	Итого
Теоретическое количество	20	20	20	20	80
Эмпирическое количество	17	23	32	8	80

Дальнейший алгоритм действий прост.

Формулируем нулевую и альтернативную гипотезы и задаем уровень значи­мости α=0,05.

Н₀: Все страны-производители машин представлены одинаковым образом (вероятность встретить на дороге машину, произведенную, например, в США, равна вероятности встретить машину, произведенную в Европе или в Юго-Восточной Азии, и т. д.).

Н₁: Различные страны-производители машин представлены неодинаковым образом (вероятность встретить машину, произведенную в США, не равна вероятности встретить машину, произведенную в Европе, в Юго-Восточной Азии и т. д.).

Затем вычисляется сумма отклонений между наблюдаемыми и теоретиче­скими значениями по формуле:

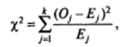
где Оj — наблюдаемые (observed), или эмпирические, значения (частоты) для каждой из категорий таблицы 3.2; Еj — ожидаемые (expected), или теоретиче­ские, значения (частоты) для каждой из категорий таблицы 3.2; k — количест­во категорий в таблице 3.2.

С учетом введенных обозначений перейдем от таблицы 3.2 к таблице 3.3.

Подставим соответствующие значения Оj и Еj в расчетную формулу:

 

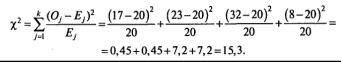
Таблица 3.3

СТУДЕНТЫ ГОЛОСУЮТ НОГАМИ, ИЛИ ТЕСТ ФРИДМАНА

Уже знакомый нам преподаватель предположил, что одни занятия студенты прогуливают чаще, а другие — реже. Он связался с другими преподавателями и в конце семестра получил данные о числе пропусков занятий у студентов своей группы еще по двум предметам; Полученные результаты приведены в таблице 5.2. Таблица содержит сведения о числе пропусков занятий для сту­дентов одной группы по трем предметам: А, В, С.

Можно ли на основании полученных данных утверждать, что студенты пропускают занятия выборочно, в зависимости от изучаемого предмета?

Ответ на этот вопрос может быть получен несколькими путями. Первый путь связан с попарным сравнением числа пропусков по предметам А, В, С между собой. Для этого потребуется трижды использовать, например, тест Вилкоксона.

Существует другая возможность, предложенная Фридманом. Тест Фридмана позволяет сравнивать результаты трех и более измерений, полученных на одной и той же выборке. С его помощью можно определить, отличаются ли получен­ные результаты друг от друга, без выявления направления отличий³.

³ В общем случае тест Фридмана рассматривается как непараметрический аналог двухфакторного дисперсионного анализа (Two-way ANOVA by ranks). Он позволяет оценить эффект воздей­ствия двух факторов на измеряемую величину. В нашем примере измеряемая величина — число пропусков занятий. Она находится под воздействием двух факторов. Первый фактор - «предме­ты/ преподаватели», имеющий три уровня. Второй фактор - «студенты», имеющий 20 уровней.

Таблица 5.2

Число пропусков занятий по предметам А, В и С

Студент	Предметы   Предметы			Студент	Предметы
	А	В	С		А	В	С
1	3	5	7	11	2	4	1
2	5	2	3	12	2	0	3
3	2	6	4	13	5	3	0
4	6	7	5	14	0	3	3
5	7	1	3	15	3	7	5
6	5	0	2	16	0	5	4
7	0	4	3	17	3	4	6
8	4	5	6	18	1	6	4
9	1	2	3	19	3	5	3
10	5	7	7	20	5	1	2

 

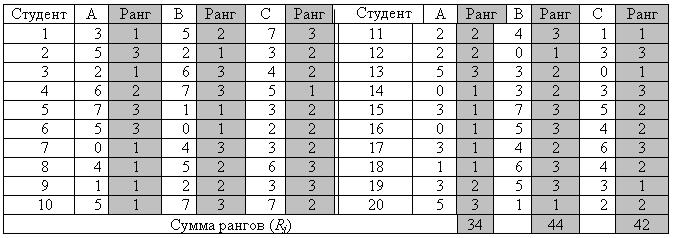
Тест Фридмана, как и тест Вилкоксона, также использует процедуру ранжирования результатов измерений, но ранжирование происходит не по верти­кали, как в тесте Вилкоксона, а по горизонтали, от измерения к измерению. Например, первый студент по предмету А пропустил 3 занятия, по предмету В — 5 занятий, по предмету С — 7 занятий. Если эти результаты проранжировать, то получим ранги 1, 2, 3 (первый ранг приписывается наименьшему значению).

Перепишем таблицу 5.2 с указанием рангов для каждого студента. Получим таблицу 5.3, в которой выделены значения рангов для каждого студента.

Если предположить, что число пропусков мало меняется от предмета к предмету, то суммы рангов для каждого из столбцов также должны мало отличаться друг от друга. В том случае, если одни предметы пропускаются чаще, а другие реже, суммы рангов в каждом из столбцов будут существенно отличаться друг от друга.

Мерой отличия сумм рангов друг от друга является значение Х² _r, вычисляемое по следующей формуле:

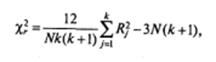
где N — число строк в таблице (размер выборки); k — число столбцов в таблице (количество измерений); R_j — сумма рангов, соответственно, для первого, второго и третьего столбцов.

Таблица 5.3

Число пропусков занятий по предметам А, В, С и их ранги

 

Найденное значение Х² _{r эмпир} сравнивается с критическим значением Х² _{r критич} , которое находится по уже знакомой таблице для теста Х²(табл. 2, Приложение 2) для выбранного уровня значимости а и числа степеней свободы df =( k -1).

В том случае, если Х² _{r эмпир} меньше Х² _{r критич}. нет оснований, чтобы отвергнуть нулевую гипотезу.

В том случае, Х² _{r эмпир}  больше или равно Х² _{r критич}, нулевая гипотеза отвергается и принимается альтернативная.

Итак, выбираем уровень значимости α = 0,05 и формулируем нулевую и альтернативную гипотезы.

Н₀: Пропуски студентами занятий носят случайный характер и не опреде­ляются изучаемым предметом.

Н₁: Пропуски студентами занятий носят неслучайный характер и определя­ются тем, какой предмет они изучают (двусторонняя критическая область).

По данным таблицы 5.3, имеем:

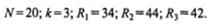
Подставляем эти значения в формулу для вычисления Х² _r:

 

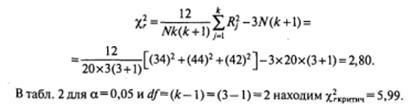
Так как Х² _{r эмпир} = 2,80 меньше Х² _{r критич} = 5,99, нет оснований, чтобы отвергнуть нулевую гипотезу. Пропуски студентами занятий носят случайный характер и не определяются изучаемым предметом.

Сейчас еще один пример.

В ходе одного из экспериментов по когнитивной психологии фиксировалось время (в минутах), которое требуется лабораторной мыши для выхода из лаби­ринта в четырех различных экспериментальных условиях.

Для группы из четырех мышей были получены следующие значения времени в зависимости от экспериментальных условий А, В, С, D (табл. 5.4).

Таблица 5.4

От условий эксперимента

 

	Условия эксперимента
	А	В	С	D
Мышь 1	5	3	2	4
Мышь 2	4	3	2	5
Мышь 3	6	2	3	5
Мышь 4	6	4	3	5

Проранжируем результаты в каждой строке, запишем их в новую таблицу (табл. 5.5) и найдем сумму рангов для каждого столбца.

Таблица 5.5

Значения ожидаемых частот

 

Наркоманы	Работающие	Безработные	Итого
Женатые	224x125 Е11= 450 =62,2	226x125 Е12= 450 =62,8	125
Разведенные	224x162 Е21= 450 =80,6	226x162 Е22=  450 =81,4	162
Не состоявшие в браке	224x163 Е31=  450 =81,1	226x163 Е32= 450  =81,9	163
Итого	224	226	450

Подставим значения наблюдаемых и ожидаемых частот в формулу для вычисления Х²:

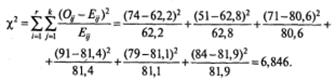
В табл. 2 находим значение Х²_критич для α=0,05 и числа степеней свободы

df =( r -1)( k -1)=(3-1)(2-1)=2: Х²_критич =5,99.

Поскольку Х²_эмпир > Х²_критич. нулевая гипотеза отвергается и принимается альтернативная. Семейное положение работающих мужчин-наркоманов отличается от семейного положения безработных мужчин-наркоманов.

 

 

ВКЛЮЧАЕМ КОМПЬЮТЕР...

В переменной «Происхождение» (origin) означим Израиль как 1, все другие страны как 2. Переменная «Блондинка» (blond) содержит сведения о цвете волос: 1 — блондинка, 0 — нет. Дальнейшая последовательность действий и получаемый результат показаны на рис. 6.1-6.3⁶.

⁶ Программа SPSS предоставляет большой набор возможностей по работе с таблицами сопряженности. Рассмотрение их в полном объеме выходит за рамки этой книги.

Рис. 6.1. Выбор требуемой статистической процедуры

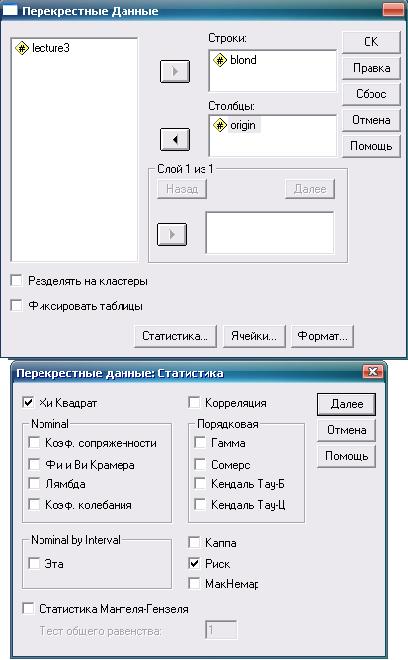
Рис. 6.2. Тест Х² для двух независимых выборок: необходимые действия и настройки

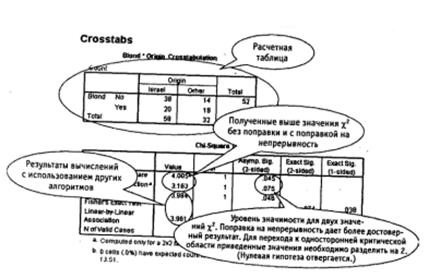
Рис. 6.3. Тест Х² для двух независимых выборок: результат

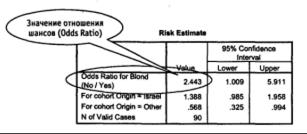
Рис. 6.3. Окончание

 

Рассмотрим еще один пример, посвященный семейному положению работающих и неработающих наркоманов. В случае больших выборок результаты в расчетной таблице зачастую удобнее представлять не в виде абсолютных значений, а в виде процентов. На рис. 6.4 и 6.5 показано, как использовать эту возможность.

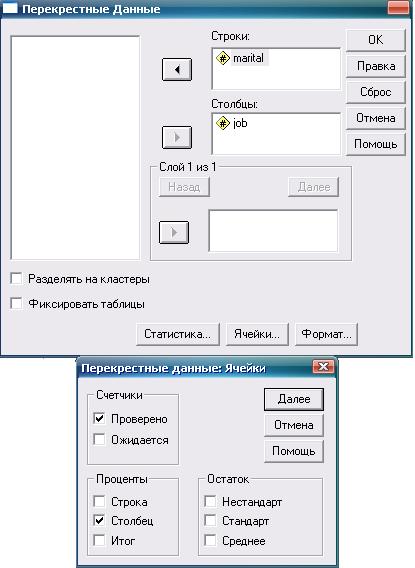
Рис. 6.4. Тест Х² для двух независимых выборок: необходимые действия и настройки

Рис. 6.5. Тест Х² для двух независимых выборок: результат (случай большой выборки)

Общий вид расчетной таблицы

	Храпят	Не храпят	Итого
Предпочитают спать на спине	8 А	3 В	11 (А+В)
Предпочитают спать не на спине	2 С	9 D	11 (C+ D)
Итого	10 (А+C)	12 (В+D)	22

Идея точного теста Фишера в следующем.

Допустим, что имеется распределение экспериментальных данных по клеткам таблицы сопряженности размером 2x2 (табл. 6.7). На основании данных можно вычислить вероятность получения такого распределения результатов.

Таблица 6.7

ИЛИ ТЕСТ ВАЛЬДА-ВОЛФОВИЦА

В Книге пророка Даниила дано безупречное описание эксперимента с ис­пользованием двух независимых выборок:

«Сказал Даниил Амелсару <...>: "Сделай опыт над рабами твоими в течение десяти дней; пусть дают нам в пищу овощи и воду для питья; и потом пусть явятся перед тобой лица наши и лица тех отроков, которые питаются царскою пищей..." Он послушался их в этом и испытывал их десять дней. По истечении же десяти дней лица их оказались красивее, и телом они были полнее всех тех отроков, которые питались царскими яствами»¹⁵.

¹⁵ Дан. 1,11-15.

Сейчас трудно сказать, чем питался царь Навуходоносор и его приближен­ные, но, видимо, предложенная Даниилом овощная диета и отказ от алкоголя в пользу воды оказались для молодых людей более полезными, чем истощающие организм и обильно сдобренные вином царские яства.

Для достижения результата юному Даниилу понадобилось всего десять дней. Современным толстякам и толстушкам, которые, не в пример Даниилу, реша­ют задачу своего похудания, для того чтобы сбросить лишние 15—20 килограм­мов своего веса, требуются недели и месяцы. Именно последнее обстоятель­ство легло в основу исследования, посвященного проверке эффективности двух различных диет. Для участия в эксперименте было отобрано две группы доб­ровольцев (по 10 человек в каждой), желающих снизить свой вес не менее чем на 20 кг. Первой группе была предложена диета А, второй — диета В. В ходе эксперимента фиксировалось время (в неделях), которое понадобилось участ­никам для достижения поставленной цели — снижения веса на 20 кг.

Результаты эксперимента представлены в таблице 6.19.

Таблица 6.19

Число решенных головоломок

Мальчики	Девочки
7	6
5	7
5	5
4	6
8	3

Если сравнить обе группы, то в них можно увидеть одинаковые (связанные) результаты. При объединении обеих групп и упорядочивании результатов ясно, в какой последовательности записывать повторяющиеся результат относящиеся к разным группам.

Здесь возможны несколько вариантов:

3	4	5	5	5	6	6	7	7	8
Д	М	М	М	Д	Д	Д	Д	М	М
3	4	5	5	5	6	6	7	7	8
Д	М	М	Д	М	Д	Д	Д	М	М
3	4	5	5	5	6	6	7	7	8
Д	М	Д	М	М	Д	Д	Д	М	М
3	4	5	5	5	6	6	7	7	8
Д	М	Д	М	М	Д	Д	М	Д	М
3	4	5	5	5	6	6	7	7	8
Д	М	Д	М	М	Д	Д	М	Д	М

Все варианты являются равноправными, но в первом из них 4 серии, следующих 6 серий и в двух последних 8 серий. Как известно, чем больше серий, тем сильнее «перемешаны» результаты, тем меньше шансов выявить различия между выборками. 

К сожалению, однозначного решения проблемы совпадающих результат не существует [Siegel, 1956]. В ряде случаев рекомендуется записать все возможные варианты упорядочивания с учетом совпадающих результатов, затем произвести статистическую проверку для каждого из них и вынести окончательное решение о судьбе нулевой гипотезы по результатам проверки [Runyon, 1977]. При этом различных вариантов записи упорядоченных результатов может быть до нескольких десятков (в нашем простом примере их уже 5)¹⁹.

¹⁹ Использование программы SPSS избавляет от этих трудностей.

 

ВКЛЮЧАЕМ КОМПЬЮТЕР...

В программе SPSS на основе сведений о размере выборок n₁и n₂ и числе серий R рассчитывается вероятность получения такого результата. Для этого использует следующая формула, меняющаяся в зависимости от того, имеем ли мы дело с четными или нечетными значениями:

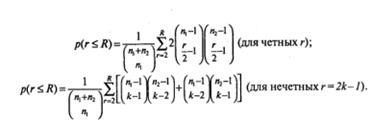
Итоговая вероятность равна сумме «четных» и «нечетных» частей этой формулы. В нашем примере n₁= n₂= 10; R =5. Значение r меняется от 2 до 5. Если r =3, это означает r =(2х2) -1, то есть k:=2. Если r =5, это означает r =(2х3) -1, то есть k =3.

 

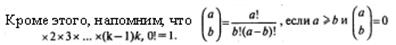
Подставим в формулу все необходимые данные.

 

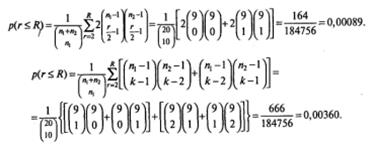
Объединяем «четный» и «нечетный» результаты:

р(r≤R) = 0,00089 + 0,00360 = 0,00449 = 0,004.

Кроме вычисленного значения вероятности (соответствующего односторонней критической области), которое сравнивается с выбранным уровнем значимости α, вычисляется значение z с учетом тех поправок, которые были рассмотрены в пара­графе 3.4:

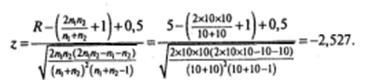
Если каждая выборка содержит более 30 значений, то различия между вычисленным значением вероятности и значением вероятности, полученным на основе z-распределения (табл. 1, Приложение 2), становится несущественным. Перейдем к программе SPSS. В переменной «Группы» (groups) принадлежность участников эксперимента к первой или второй группе обозначена как 1 или 2. В пе­ременной «Время» (time) указано время (в неделях), в течение которого вес был снижен на 20 кг. Дальнейшая последовательность действий и конечный результат показаны на рис. 6.17—6.19.

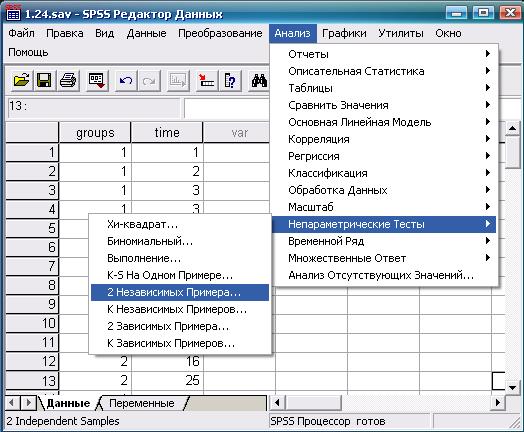
Рис. 6.17. Выбор необходимой статистической процедуры

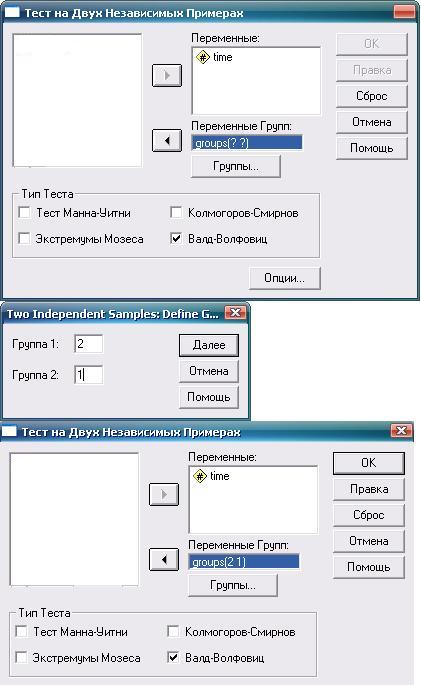
Рис. 6.18. Тест Вальда—Волфовица: необходимые действия и настройки.

Рис. 6.19. Тест Вальда—Волфовица: результат

 

Результаты теста на эмпатию

Андроиды	Люди
17	27
5	20
19	20
47	18
15	29
8	32
8	28
52	16
39	30

Можно ли на основании полученных данных утверждать, что тест Войт − Кампфа в состоянии эффективно выявлять андроидов?

Казалось бы, приведенный пример мало отличается от тех, которые мы рассматривали для случая двух независимых выборок. Однако здесь присутствует одна особенность, для учета которой Мозес предложил тест, носящий его имя

Рассмотрим гистограммы двух распределений (рис. 6.20 и 6.21).

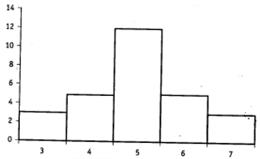
Рис. 6.20. Гистограмма 1

Оба распределения имеют совпадающие значения среднего, моды и медианы. Основное различие между ними в том, что второе распределение боле «растянуто» по горизонтальной оси (значение дисперсии для второго распределения больше, чем для первого). В параметрической статистике для сравнения «ширины» двух различных нормальных распределений чаще всего используется F тест Фишера, основанный на сравнении дисперсий.

В случае маленьких выборок вычисление и сравнение дисперсий теряет свой смысл, однако здесь также возникают ситуации, когда необходимо сравнить друг с другом «ширину» распределения результатов в каждой из них. Такая задача становится актуальной в том случае, если у исследователя есть основания предполагать, что в одной из выборок реакции испытуемых (респондентов), например на экспериментальное воздействие, носят более близкий к краю (экстремальный) характер. Такое предположение чаще всего возникает в том случае, когда независимые выборки существенным образом отличаются друг от друга по какому-либо показателю. Например, можно предположить, что определенные поведенческие и эмоциональные реакции в группе женщин, подвергшихся сексуальному насилию, будут носить более полярный характер (от полной эмоциональной «замороженное» до бурных эмоциональных «взрывов») по сравнению с реакциями в группе обычных женщин.

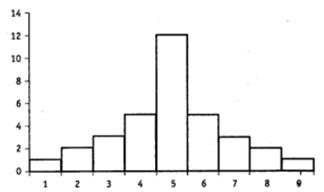
Рис. 6.21. Гистограмма 2

По сути дела, в тесте экстремальных реакций Мозеса одна выборка высту­пает в качестве контрольной группы, а другая — в качестве экспериментальной. В качестве экспериментальной группы выбирается та, в которой, по предпо­ложению исследователя, результаты будут носить более экстремальный харак­тер (в нашем случае это группа андроидов)²¹.

²¹ Если выбор сделан неудачно, будет получен результат, лишенный смысла.

В качестве меры изменчивости, позволяющей сравнивать «ширину» обеих выборок, используется один из наиболее редко применяемых статистических показателей — размах (Span). Размах S определяется как разность между мак­симальным и минимальным значением плюс единица²²: S =Х_mах —Х_min + 1 (табл. 6.20 и рис. 6.22).

Рис. 6.22. Иллюстрация к тесту экстремальных реакций Мозеса

²² Добавка единицы повышает точность вычисления размаха.

В тесте экстремальных реакций Мозеса размах (по отношению к рангу) вычисляется для контрольной группы. Затем, на основе значения размах сведений о размере выборок и других показателях, вычисляется вероятие получения такого результата.

Если полученное значение вероятности оказывается меньшим или равныv выбранному значению уровня значимости а, то нулевая гипотеза отвергается. Если значение вероятности больше выбранного значения уровня значимости α, то оснований отвергнуть нулевую гипотезу нет.

Применим тест экстремальных реакций Мозеса к нашим данным.

Выберем уровень значимости α =0,05 и сформулируем нулевую и альтернативную гипотезы.

Н₀: Между людьми и андроидами нет различий в значениях эмпатии.

Н₁: Значения эмпатии у андроидов носят более экстремальный характер по сравнению со значениями эмпатии у людей (односторонняя критическая область²³).

²³ В этом тесте использование двусторонней критической области невозможно.

Объединим обе выборки, расположим значения эмпатии в порядке возрастания, присвоим каждому значению свой ранг²⁴ и укажем кому — людям (Л) или андроидам (А) — принадлежит то или иное значение (табл. 6.23).

Таблица 6.23

Возраст начала курения

Коренные израиль­тяне (евреи)	Израильтяне — бедуины	Иммигранты из б. СССР	Иммигранты из Эфиопии
10	7	9	13
12	6	7	10
11	8	12	11
12	10	11	14
10	11	6	12
13	9	13	11
13	12	10	13

Из курящих подростков, представляющих коренных израильтян-евреев, израильтян-бедуинов, иммигрантов из бывшего СССР и иммигрантов из Эфиопии были сформированы четыре независимые выборки. В таблице 7.10 приведены сведения о возрасте начала курения для каждой из выборок.

Можно ли утверждать, что подростки, принадлежащие к различным куль­турно-этническим группам, начинают курить в разном возрасте?

Поскольку алгоритм дальнейших действий нам уже известен, сразу присту­паем к использованию теста Крускала—Уоллиса.

Выберем уровень значимости α =0,05 и сформулируем нулевую и альтерна­тивную гипотезы.

Н₀: Нет отличий в возрасте начала курения у израильских подростков — пред­ставителей различных этнокультурных групп.

Н₁: Израильские подростки — представители различных этнокультурных групп начинают курить в различном возрасте (двусторонняя критическая об­ласть).

Как и в предыдущем примере, объединим все выборки в одну, запишем содержащиеся в выборках значения в порядке возрастания и проранжируем их (табл. 7.11).

 

 

Таблица 7.11

Определение медианы

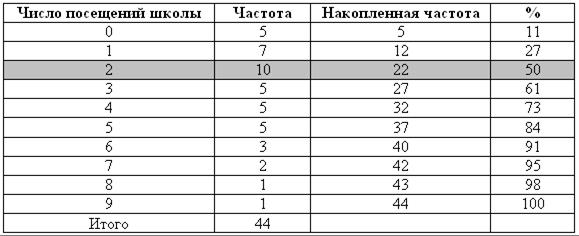
Определим для каждой выборки, сколько значений больше медианы (боль­ше чем 2) и сколько меньше медианы или равно ей (табл. 7.20).

Таблица 7.20

КРАСОТА НА ВСЕ ВРЕМЕНА, ИЛИ

Результаты ранжирования

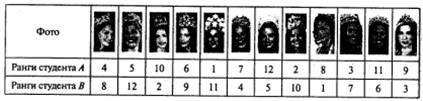
Существует ли корреляционная связь между результатами двух ранжиро­ваний?

Разумеется, ответ на данный вопрос можно получить с помощью вычи­сления коэффициента ранговой корреляции Спирмена. Однако в середине 1940-х гг. Кендалл предложил новый подход к определению корреляционной связи между ранговыми переменными. В том случае, если выборка небольшая, удобнее иметь дело с корреляцией по Кендаллу, чем с корреляцией по Спирмену.

Идея корреляции по Кендаллу достаточно проста.

Допустим, мы упорядочили группу людей по росту — от максимального до минимального и узнали значения веса каждого из них. Теперь можно получить два ранговых ряда — для роста и для веса. Если предположить, что чем больше рост, тем больше вес, то изменение рангов рос­та будет совпадать с изменением рангов веса. Например, первому рангу по росту будет соответствовать первый ранг по весу, второму рангу по росту — второй ранг по весу и т. д. Однако эта последовательность может быть нарушена (человек может быть высоким, но очень худым, или низкорослым, но очень тучным), и вместо совпадения рангов для роста и веса мы получим инверсию рангов (перестановку): например, рост уменьшился, а вес увеличился.

Если оба ранговых ряда полностью совпада­ют, то это соответствует коэффициенту корре­ляции +1. Если один ряд выглядит «наоборот» по отношению к другому, мы имеем сплошные инверсии, что соответствует коэффициенту корреляции — 1.

В обычных случаях, если сравнивать два ряда рангов, в них встречаются как совпадения, так и инверсии. Кендалл предложил простую формулу для вычис­ления коэффициента корреляции на основе числа совпадений и инверсий.

Вернемся к таблице 8.7. Для студента А запишем ранги по порядку — от 1 до 12 и укажем соответствующие ранги для студента В. Получим таблицу 8.8.

 

Таблица 8.8

Результатов тестирования

Иврит (ранги)	1	2	3	4,5	4,5	6	7	8	9	10 *
Логическое мыш­ления (ранги)	2	3	10	1	4,5	4,5	6	8	9	7
Совпадения	7	6	0	5	4	4	3	1	0	0
Инверсии	1	1	6	0	0	0	0	1	0	0

Обратите внимание! При подсчете совпадений и инверсий связанные ранги учитываются только один раз. Например, правее ранга 2 расположено 8 значений, больших, чем 2; 3; 10; 4,5; 4,5; 6; 8; 9; 7. Но поскольку значения 4,5 и 4,5 образованы связанными рангами, они берутся в расчет только один раз. Поэтому фактическое число совпадений для ранга 2 будет не 8, а 7.

Сумма совпадений = (7 + 6 + 0 + 5 + 4 + 4 + 3 + 1 + 0 + 0) = 30

Сумма инверсий = (1 + 1 + 6 + 0 + 0 + 0 + 0 + 1 + 0 + 0) = 9

S = (Сумма совпадений – Сумма инверсий) = (30 - 9) = 21

При наличии связанных рангов используется иная формула для вычисления коэффициента ранговой корреляции Кендалла τ:

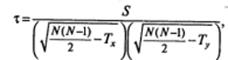
где Т_х=0,5∑ t_x(t_x -1), Т_у=0,5∑ t_у(t_у -1), t_x, t_у — размер каждой группы связанных

рангов (количество повторяющихся значений) в первой (х) и второй (у) строках.

В табл. 8.12 в первой строке (ранги оценок по ивриту) есть одна группа свя­занных рангов (4,5 и 4,5). Здесь t_x =2 и Т_х = 1/2[2(2 -1)] = 1.

Аналогичная ситуация во второй строке — одна группа связанных рангов, включающая два значения: 4,5 и 4,5. Поэтому t_у =2 и Т_у =1/2[2(2 -1)] = 1.

Подставим все необходимые значения в формулу для вычисления τ:

 

Проверим полученные значения коэффи­циента ранговой корреляции Кендалла на значимость.

Вначале проверим на значимость значение τ для первого примера (ранжирование фото­графий): τ =–0,485.

Выберем уровень значимости а=0,05 и сформулируем нулевую и альтернативную гипотезы.

Н₀: Коэффициент корреляции между ре­зультатами оценивания женской привлека­тельности представителями двух различных культур равен нулю.

Н₁: Коэффициент корреляции между ре­зультатами оценивания женской привлека­тельности представителями двух различных культур отличен от нуля (двусторонняя кри­тическая область).

Для проверки коэффициента ранговой корреляции Кендалла на значимость используется несколько подходов, в зависимости от значения N.

Если N > 10, то вначале вычисляется значение z :

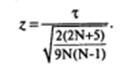
Затем по таблице z-распределения (см. табл. 1, Приложение 2) определяет­ся вероятность (для односторонней критической области), соответствующая полученному значению. Если эта вероятность оказывается больше выбранно­го уровня значимости а, нет оснований отвергнуть нулевую гипотезу. Если найденная вероятность меньше выбранного уровня значимости α или равна ему, нулевая гипотеза отклоняется и принимается альтернативная.

Вычислим z для τ = –0,485 и N= 12.

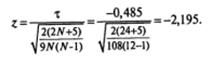
В таблице 1 (Приложение 2) для z -распределения, находим, что значению z = – 2,195 соответствует вероятность р =0,0143.

В том случае, если критическая область двусторонняя (как в нашем случае), значение вероятности необходимо удвоить: р =0,0286.

Поскольку значение уровня значимости α =0,05 больше, чем р =0,0286, нулевая гипотеза отклоняется и принимается альтернативная. Существует значимая, отличная от нуля корреляционная связь между результатами оценивания женской привлекательности представителями двух различных культур.

Проверим на значимость результат, полученный во втором примере (случай связанных рангов): τ = 0,477. 

Выберем уровень значимости α =0,05 и сформулируем нулевую и альтернативную гипотезы.

Н₀: Коэффициент корреляции между уровнем знания иврита и показателями логичности мышления у новых иммигрантов равен нулю.          

Н₁: Коэффициент корреляции между уровнем знания иврита и показателями логичности мышления у новых иммигрантов отличен от нуля (двусторонняя критическая область).         

Для случая малых выборок (N ≤ 10) существует специальная таблица, содержащая значения р (односторонняя критическая область) в зависимости значений т и N (см. табл. 12, Приложение 2).

Из таблицы 12 находим, что для τ = 0,477 и N= 10 значение р лежит между р =0,036 (для τ = 0,467) и р =0,023 (для τ = 0,511). Примем р =0,030. Поскольку альтернативная гипотеза сформулирована для случая двусторонней критической области, удваиваем это значение: р =0,060.

Полученное значение вероятности оказалось больше, чем α =0,05. Оснований отвергнуть нулевую гипотезу нет. Коэффициент корреляции между уровнем знания иврита и показателями логичности мышления у новых иммигран­тов — выпускников языковых курсов незначимо отличается от нуля⁹.

 

ВКЛЮЧАЕМ КОМПЬЮТЕР...

Результаты ранжирования фотографий поместим в переменные «Ранг 1» (range 1) и «Ранг 2» (range 2) Дальнейшие действия и получаемый результат показаны на рис. 8.6-8.8.

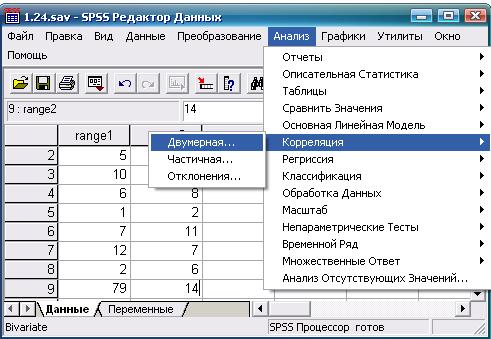
Рис. 8.6. Выбор требуемой статистической процедуры

 

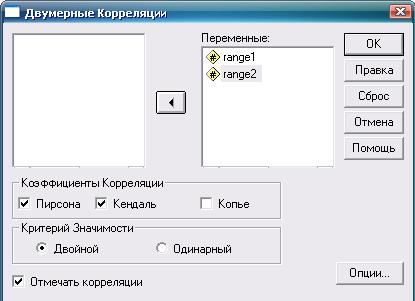
Рис. 8.7. Коэффициент ранговой корреляции Кендалла: необходимые действия и настройки

 

 

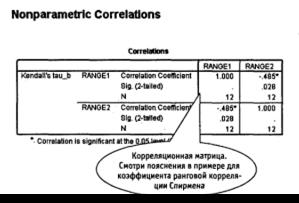
Рис. 8.8. Коэффициент ранговой корреляции Кендалла: результат

Рассмотрим пример со связанными рангами. В переменной «Иврит» (Нebrew) поместим результаты экзамена по ивриту, а в переменной «Логика» (logic) све­дения об уровне логического мышления. Результат вычислений для случая двусторонней и односторонней критических областей показан на рис. 8.9.

Обратите внимание! Один и тот же коэффициент корреляции, в зависимо­сти от того, как сформулирована альтернативная гипотеза, в одном случае признается незначимым, а в другом — значимым!

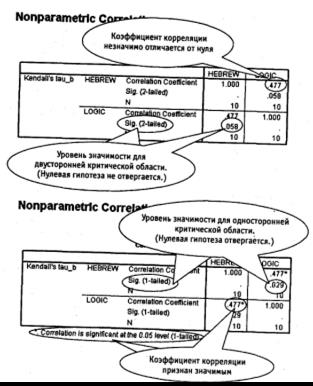
Рис. 8.9. Коэффициент ранговой корреляции Кендалла: результат

 (пример для связанных рангов)

ПРИЛОЖЕНИЯ

Приложение 1

Таблица вероятностей для биномиального теста

(указаны значения после запятой для случая р=q=0,5)

 

 

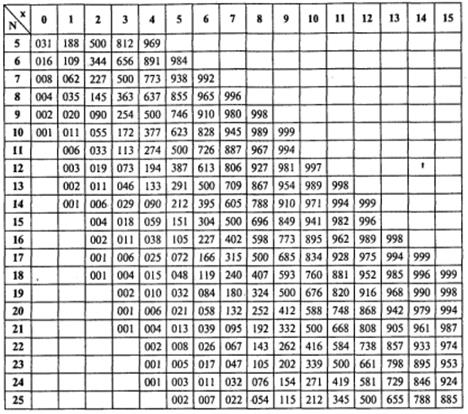
Таблица 4

Тест последовательностей

Назначение теста. Проверка случайного характера последовательности ди­хотомических значений.

Для анализируемой последовательности, образованной дихотомической переменной, принимающей, например, значения 0 и 1, определяется, сколько раз в ней встречаются значение 0 (n₀), значение 1 (n₁) и количество серий r из нулей и единиц (включая единичные значения нулей и единиц).

На основании полученных данных о n ₀ , n ₁ и r вычисляется значение z:

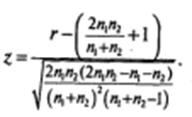
В случае маленькой выборки (менее 50 значений) используются поправки:

1. Если 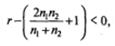 формула принимает вид:

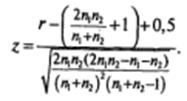
2. Если 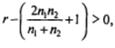  формула принимает вид:

 

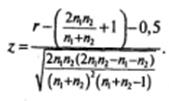
По таблице z-распределения определяется вероятность, соответствующая вычисленному значению z для односторонней критической области.

Программный синтаксис (для дихотомической переменной 0,1):

NPAR TEST

/RUNS (1) = var
/MISSING ANALYSIS.

Биномиальный тест

Назначение теста. Сравнение частоты появления двух дихотомических переменных, имеющих вероятности p и q =(1- р), если после N независимых испытаний частота появления первой из них равна n ₁, частота появления второй из них равна n ₁ (N= n ₁ + n ₂).

Вероятность полученного результата рассчитывается по следующей формуле (формула Бернулли), где

m = min (n₁, n₂):

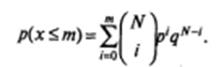
В этом случае, когда N  > 25, возможно применение формулы, связанной с вычислением z:

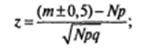
(m + 0,5) используется в том случае, когда х < Np;

(m – 0,5) используется в том случае, когда х > N p.

По таблице z -распределения определяется вероятность, соответствующая вычисленному значению z для односторонней критической области.

Программный синтаксис (для случая р=q=0,5):

NPAR TEST

/BINOMIAL (.50) = var
/MISSING ANALYSIS.

Пустое брюхо к науке глухо

Опросите 15—20 своих друзей и знакомых из числа студентов, получающих стипендию. Узнайте, сколько они тратят в день на питание накануне получения стипендии и через несколько дней после ее получения. С помощью теста Вилкоксона проверьте, оказывает ли стипендия существенное влияние на студенческий бюджет.

Кто больший патриот?

Обойдите свое жилище и отметьте, сколько вещей из числа тех, которые вас окружают, отечественного производства, а сколько являются импортными. Включите в список 7—10 предметов (мебель, холодильник, телевизор, одежду и др.). Попросите сделать то же самое своего друга (подругу) и с помощью точного теста Фишера сравните оба результата.

9. Вот такое кино...

Вернитесь ко второму заданию и разбейте список из 30—40 кинофильмов не только на 3—4 категории по жанрам, но также на две группы: «отечествен­ный» — «зарубежный». С помощью теста х2 определите, есть ли различия ме­жду двумя группами фильмов.

Краткость — сестра таланта?

Найдите в Интернете сведения о длительности 15—20 отечественных и 15— 20 зарубежных фильмов, вышедших за последнее время. Сравните полученные результаты с помощью теста Манна—Уитни.

Друзья приходят или уходят?

Вам знаком сайт «Одноклассники»? Тогда вперед!

Задайтесь четырьмя возрастными категориями по возрастанию (например, до 25 лет, 26 − 35 лет, 36 − 45 лет, старше 46 лет). Для каждой возрастной катего­рии с помощью сайта «Одноклассники» случайным образом отберите по 5 − 6 человек. Зайдите к каждому из них «в гости» и определите, сколько человек входит в круг его друзей. С помощью теста Джонкхиера—Терпстра проанали­зируйте полученные данные (число друзей для каждой выборки и соответст­вующей возрастной категории). Можно ли говорить о существовании здесь тенденции, связанной с изменением числа друзей с возрастом?

Что сегодня по «ящику»?

Составьте список из 10 − 15 популярных телевизионных передач или сериа­лов, которые вам знакомы. Проранжируйте список по степени привлекатель­ности для вас включенных в него передач. Попросите сделать то же самое ва­шего друга (подругу). С помощью коэффициента ранговой корреляции Кендалла
определите, насколько ваши мнения совпадают. Можно ли утверждать, что полученный результат неслучаен?   

В тиши музейных коридоров

В пятерку крупнейших музеев мира входят парижский Лувр, нью-йоркский Метрополитен-музей, лондонская Национальная галерея, музей Прадо в Мадриде и петербургский Эрмитаж. Если бы у вас была возможность побывать в каждом из них, каким был бы порядок ваших предпочтений? Спросите об этом еще у 6 − 7 человек и затем с помощью коэффициента конкордации Кендалла определите, насколько совпадают ваши мнения. Проверьте полученный ре­зультат на значимость.

 

Доктор (РhD) Александр Резник работает на отделении социальной работы Универ­ситета Бен Гурион в Негеве (Израиль). Область его научных интересов: сравни­тельная аддиктология, психология меж­культурных различий, социальная работа с наркозависимыми в мультикультурной среде, а также методология эксперименталь­ных исследований в социальных науках. Имеет более 50 научных публикаций в России, США, Израиле и др.

Многолетний опыт научной и преподавательской деятельно­сти А. Резника в России и Израиле включает в себя препо­давание таких курсов, как «Математико-статистические мето­ды в психологии», «Теория и практика психологического экс­перимента», «Теоретические основы психологического тестиро­вания» и др.

В настоящее время сочетает научно-исследовательскую деятельность с консультационной в области статистики, ме­тодов исследований и использования программы SPSS в аддиктологии и социальной работе.

 

Методы непараметрической статистики позволяют получать обоснованные статистические выводы при наличии крайне небольшого числа испытуемых. Кроме того, простота процесса математической обработки результатов — в ряде случаев необходимые вычисления можно сделать в уме.

 

А. Д. РЕЗНИК

КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ,

НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ