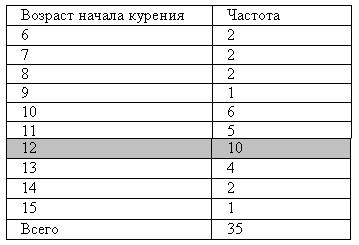
Как видно из таблицы, чаще всего подростки начинают курить в 12 лет (это значение возраста встречается чаще всего — 10 раз). Поэтому мода возраста начала курения — 12 лет.
Новая таблица содержит ту же самую информацию, что и предыдущая, но она заметно короче, данные в ней упорядочены по возрастанию, и с ней удобней работать.
Медиана (Ме) представляет собой значение, которое делит упорядоченные данные пополам таким образом, что одна половина данных оказывается меньше медианы, а другая — больше.
Нахождение медианы не носит столь наглядного характера, как нахождение моды. Для определения медианы приходится прибегать к дополнительным преобразованиям и вычислениям. Во-первых, дополним таблицу 1.2 еще двумя столбцами (графами) и получим таблицу 1.3.
В первом из дополнительных столбцов запишем значения так называемых «накопленных» (или кумулятивных) частот. Представьте, что мы обходим строй из 35 подростков, которые стоят в шеренгах в зависимости от возраста начала курения. В первой шеренге (6 лет) два человека. Во второй (7 лет) тоже два и т. д. Наша задача — подсчитать, сколько подростков при таком «обходе войск» осталось за нашей спиной. После первой шеренги за нашей спиной два человека. После второй — уже четыре (два в первой шеренге и два во второй) и т. д. Это и будут накопленные частоты. Очевидно, после конца «обхода» за нашей спиной будет 35 человек.
Во-вторых, запишем в следующую графу, какой процент от 35 подростков составляет каждое значение накопленных частот.
Таблица 1.3
Вычисление медианы
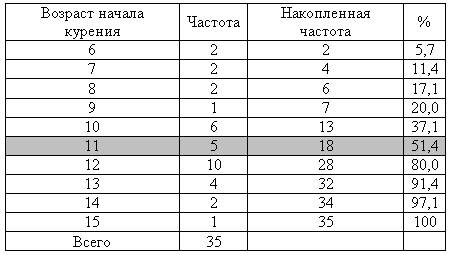
Попытаемся понять смысл полученного в последней графе результата. При переходе от шеренги «10 лет» к шеренге «11 лет» за плечами остается 37,1% всех результатов. А при переходе от шеренги «11 лет» к шеренге «12 лет» за плечами уже 51,4%. Медиана — это та точка, которая делит все данные в отношении 50:50. Очевидно, требуемая точка где-то внутри шеренги «11 лет». То есть Ме = 11.
На этом можно остановиться, хотя обычно для вычисления медианы используются более сложные вычисления.
Наиболее популярной мерой центральной тенденции является среднее (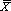 
).
Для нахождения среднего используется простая формула, смысл которой в том, чтобы сложить все значения (в нашем случае значения возраста начала курения) и разделить полученный результат на число значений (в нашем случае 35).
Дальше можно идти двумя путями.
Во-первых, начать непосредственно складывать все 35 значений возраста из первой таблицы.
Во-вторых, догадаться, что если некоторые значения возраста встречаются несколько раз, то можно воспользоваться данными из таблицы 1.2 и перейти от сложения повторяющихся значений к умножению этих значений на число повторов (например, возраст 13 лет встречается в первой таблице четыре раза, то вместо 13 + 13 + 13+13 записать 13x4). Тогда:
Меры центральной тенденции показывают, вокруг каких значений группируется большинство экспериментальных данных. Обычно в качестве «центра» такого группирования рассматривается среднее ( ).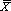
Меры изменчивости говорят о том, в какой степени полученные результаты отклоняются от «центра группирования», что чаще всего приводит к определению меры отклонения экспериментальных данных от среднего.
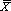В принципе, в качестве меры изменчивости можно было бы использовать среднее значение отклонений текущих значений от среднего. Для этого необходимо определить, насколько каждое значение возраста отклоняется в большую или меньшую сторону от = 10,89, затем сложить все результаты и разделить на число значений. К сожалению, этот путь невозможен, поскольку, как правило, отклонения от среднего в большую сторону (со знаком «+») и в меньшую сторону (со знаком «-») компенсируют друг друга и в сумме дают ноль.
Для решения этой проблемы лучше использовать не отклонение от среднего, а квадрат этого отклонения, потому что такая процедура позволяет избавиться от влияния знака. Вначале делается та же операция - определяется насколько каждое значение возраста отклоняется в большую или меньшую сторону от 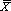= 10,89. Затем каждый из полученных результатов возводится в квадрат, все складывается и делится на число значений. Получаемая таким образом мера изменчивости называется дисперсией.
Еще раз вернемся к таблице 1.2 и дополним ее двумя графами, необходимыми для вычисления дисперсии. Получим таблицу 1.4.
Таблица 1.4
Вычисление дисперсии
На практике по ряду причин технического характера, которые мы здесь не обсуждаем, для вычисления дисперсии используется другая формула, незначительно отличающаяся от предыдущей:
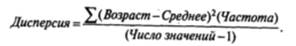
Подставим в эту формулу необходимые значения из таблицы 1.4:
К сожалению, дисперсия оказывается не очень удобным показателем меры изменчивости. Наличие в формуле квадрата меняет размерность входящих в нее величин. Например, если мы хотим определить меру изменчивости роста для группы людей, то в формуле для дисперсии будет использоваться значение (Рост — Среднее)2. Размерность этого значения см2. Но см2 — это уже размерность площади, а не длины. То есть среднее значение роста будет измерено в единицах длины, а отклонение от среднего — в единицах площади.
Для решения возникшей проблемы вместо значения дисперсии используется квадратный корень из нее. Полученное таким образом новое значение называется стандартным отклонением и является наиболее популярной мерой изменчивости. Стандартное отклонение часто обозначается как σ (сигма):
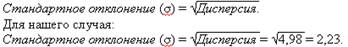
ВКЛЮЧАЕМ КОМПЬЮТЕР И ЗАПУСКАЕМ ПРОГРАММУ SPSS1
1 Мы предполагаем, что читатель имеет определенный опыт работы с этой программой. Поэтому операции по вводу данных, их кодировке и др. не рассматриваются.
После ввода данных о поле респондентов (переменная «Sех» с обозначением «1» для мальчиков и «2» для девочек) и возрасте начала курения (переменная «аgе» приступаем к их обработке. Очередность действий и конечный результат показаны на рис. 1.1-1.3.
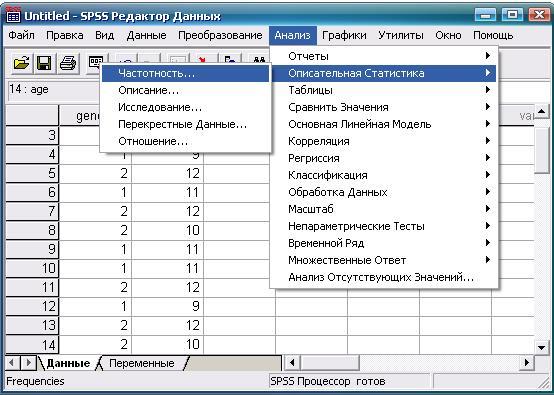
Рис. 1.1. Выбор требуемой статистической процедуры
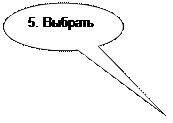
Рис. 1.2. Необходимые для обработки данных действия и настройки
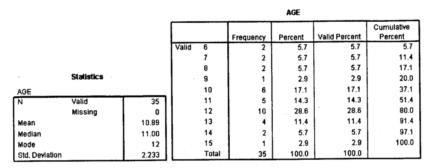
Рис. 1.3. Результат обработки
Дата: 2018-12-21, просмотров: 444.
