| Семья | IQ родителей | IQ детей |
| 1 | 90 | 100 |
| 2 | 90 | 90 |
| 3 | 90 | 95 |
| 4 | 95 | 90 |
| 5 | 95 | 95 |
| 6 | 95 | 100 |
| 7 | 100 | 105 |
| 8 | 100 | 90 |
| 9 | 100 | 95 |
| 10 | 105 | 105 |
| 11 | 105 | 110 |
| 12 | 105 | 100 |
| 13 | 110 | 115 |
| 14 | 115 | 105 |
| 15 | 115 | 100 |
| 16 | 115 | 115 |
| 17 | 120 | 110 |
| 18 | 120 | 125 |
| 19 | 125 | 120 |
| 20 | 125 | 110 |
Можно ли на основании приведенных данных говорить о наличии связи между IQ родителей и IQ детей?
Поиском ответов на подобные вопросы в статистике занимается корреляционный5 анализ, в рамках которого вычисляется мера связи между двумя рядами значений — коэффициент корреляции. Существует несколько видов коэффициентов корреляции; выбор одного из них зависит от того, с какими данными приходится иметь дело. В том случае, если взаимосвязь устанавливается для данных, имеющих нормальный закон распределения, чаще всего используется коэффициент корреляции Пирсона (r Пирсона).
5 От лат. correlatio— взаимосвязь.
Независимо от того, какой коэффициент корреляции применяется, все они обладают общим свойством: коэффициент корреляции никогда не может быть больше чем 1 и меньше чем — 1:
—1 ≤ Коэффициент корреляции ≤ 1.
Для того чтобы ответить на вопрос о существовании или отсутствии корреляционной связи между какими-либо данными, необязательно прибегать к вычислению соответствующего коэффициента (тем более что в ряде для этого используются довольно сложные формулы). Во многих случаях можно ограничиться графическим представлением полученных результатов в виде так называемой «диаграммы рассеяния».
Для ее построения рассмотрим пары значений «IQ родителей - IQ детей» из таблицы 1.5 и для каждой пары отложим значение IQ родителей по оси Х, а значение IQ детей по оси Y. В результате получим совокупность точек определенной конфигурации: диаграмму рассеяния (рис. 1.14). Ее форма и ориентация относительно осей X и Y позволяют сделать определенные выводы относительно характера корреляционной связи (рис. 1.15).
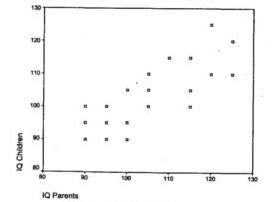
Рис. 1.14. Диаграмма рассеяния
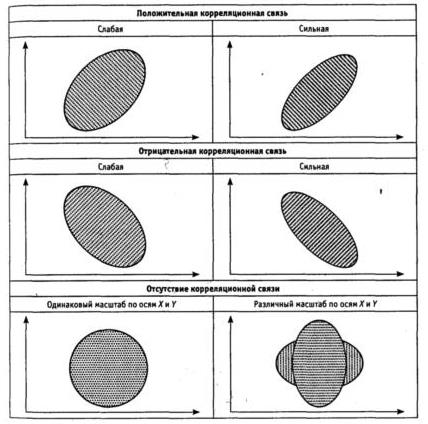
Рис. 1.15. Вид диаграммы рассеяния и характер корреляционной связи
В использовании корреляционных методов существует ряд подводных камней, о которых необходимо помнить.
1. Корреляционная связь не тождественна причинно-следственной связи.
Использование корреляции в качестве основного аргумента для установления причинно-следственных связей является одной из наиболее частых и наиболее грубых ошибок, возникающих на этапе интерпретации полученных результатов.
 Из того факта, что между А и В существует корреляционная связь, не следует, что один результат является следствием или причиной другого. В большинстве случаев для определения истинных причинно-следственных связей одной корреляционной связи недостаточно.
Из того факта, что между А и В существует корреляционная связь, не следует, что один результат является следствием или причиной другого. В большинстве случаев для определения истинных причинно-следственных связей одной корреляционной связи недостаточно.
Существует много примеров неверных выводов, сделанных вследствие отождествления корреляции с причинностью. Например, в США в свое время была установлена сильная положительная связь между загрязненностью тех или иных городских районов выбросами промышленных предприятий (сажа) и заболеваемостью туберкулезом в этих районах. На основании получений данных была развернута борьба с вредными выбросами, как основной причиной туберкулеза. Однако давно известно, что туберкулез — это в первую очередь социальная болезнь и она чаще встречается у представителей социально слабых слоев населения. Поскольку загрязненность городских районов выброса приводила к тому, что в этих районах никто не хотел жить, то цены на жилье здесь были очень низкими. В результате основными квартиросъемщиками этих районах была городская беднота, среди которой уровень заболеваемости туберкулезом изначально был выше, чем у более благополучных жителей рода [Ackoff; 1978].
2. Равенство нулю коэффициента корреляции не всегда означает отсутствие корреляционной связи.
Во-первых, формулы, используемые для вычисления коэффициента реляции, предполагают наличие корреляционной связи, близкой к линейной. Например, если рассмотреть взаимосвязь между ростом и весом, то увеличение роста, как правило, сопровождается соответствующим увеличением веса и наоборот.
В ряде случаев характер корреляционной связи не является линейным. Поэтому перед началом вычисления коэффициента корреляции имеет смысл получить диаграмму рассеяния и по ее виду определить, каков характер связи — линейный или нелинейный. Например, на рис. 1.16 приведена диаграмма рассеяния, показывающая связь между числом иммигрантов, въехавших Израиль с 1978 г., и данными о правонарушениях в области наркотиков (употребление и торговля).
Если связь нелинейная, механическое вычисление коэффициента корреляции может ничего не дать. Нелинейная связь требует использования более сложных методов вычисления.
Во-вторых, негомогенные (неоднородные) выборки6 зачастую могут создавать видимость отсутствия связей. Например, в выборке, состоящей из мужчин и женщин, может отсутствовать связь между длительностью курения (в годах) и количеством ежедневно выкуриваемых сигарет. Но эта связь может быть обнаружена для мужской и женской частей выборки по отдельности (рис. 1.17).
6 Подробнее об этом понятии см. ниже.
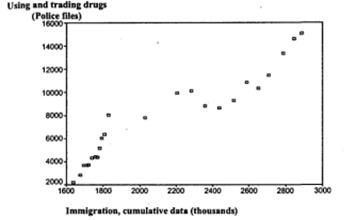
Рис. 1.16. Пример нелинейной корреляционной связи
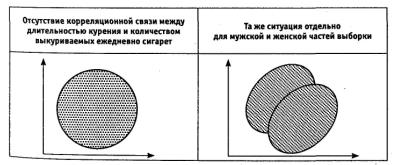
Рис. 1.17. Диаграммы рассеяния для негомогенной выборки:
видимость отсутствия корреляции
3. Наличие отличного от нуля коэффициента корреляции не всегда означает наличие корреляционной связи.
В негомогенных выборках могут быть обнаружены ложные корреляции. Например, можно обнаружить связь между длительностью поиска работы и показателем уверенности в себе — чем дольше ищется работа, тем меньше уверенность в себе. Однако, если рассмотреть отдельно мужскую и женскую части выборки, то выявленную ранее связь можно не обнаружить (рис. 1.18):
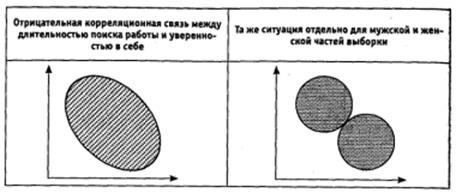
Рис. 1.18. Диаграммы рассеяния для негомогенной выборки: видимость наличия корреляции
Вернемся к вопросу о связи между интеллектом родителей и интеллектом детей. Если эта связь установлена, то можно попытаться решить другую задачу — предсказать, каким может быть интеллект будущего ребенка, если известно значение IQ его родителей.
Решением задач предсказания и оценивания в статистике занимается регрессионный анализ. У его истоков стоял Френсис Гальтон, английский учёный-энциклопедист ХIХ в., который считал, что антропометрические и интеллектуальные характеристики людей в последующем поколении возвращаются (регрессируют) к средним для популяции показателям. Иначе говоря, если рост родителей значительно выше среднего, то, скорее всего, рост их детей будет также выше среднего, но ниже роста родителей. Таким образом через несколько поколений произойдет регрессия: значение роста вернется к среднему для популяции значению. По мысли Гальтона, те же правила действуют и в отношении интеллекта — у гениальных родителей рождаются дети с высоким интеллектом, но его уровень ниже, чем уровень интеллекта родителей. Несмотря на то, что современные методы регрессионного анализа далеко отошли от идей Гальтона, само название метода сохранилось.
В результате регрессионного анализа выводится формула, в которую можно подставлять значения, например, IQ родителей и получать предполагаемые значения IQ детей. Существуют способы минимизации ошибок подобного оценивания и повышения его надежности и достоверности.
Для нашего примера эта формула будет иметь вид:
IQдет=0,667х IQрод+32,188
Если IQ родителей, например, 115, то, подставляя это значение в формулу, можно предсказать возможное значение IQ (будущего) ребенка:
IQдет=0,667х 115+32,188≈110
ВКЛЮЧАЕМ КОМПЬЮТЕР...
Для получения диаграммы рассеяния поместим данные о IQ родителей в переменную «Родители» (parents), а данные о IQ ребенка — в переменную «Ребенок» (child). Дальнейшая последовательность действий и конечный результат показаны на рис. 1.19-1.21.

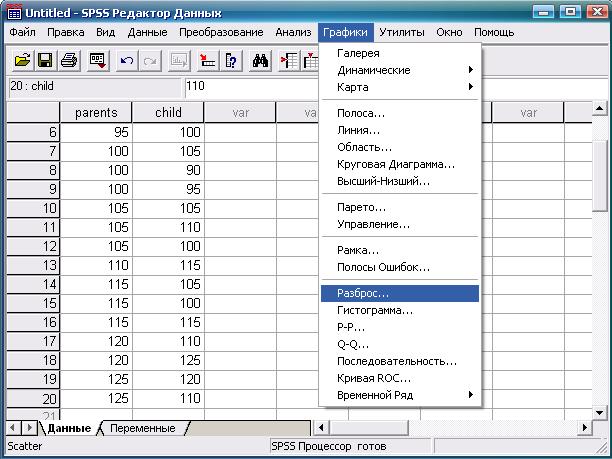
Рис. 1.19. Выбор требуемой статистической процедуры


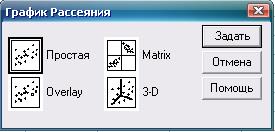
Рис. 1.20. Необходимые для получения диаграммы рассеяния действия и настройки



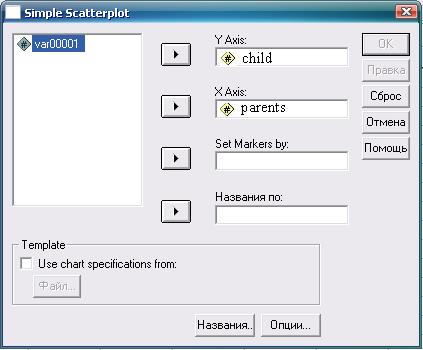
Рис. 1.20. Окончание
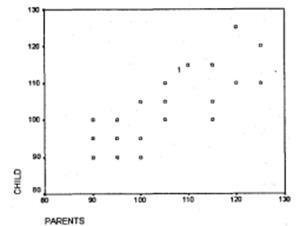
Рис. 1.21. Диаграмма рассеяния: результат
КТО БОЛЕЕ КОМПАНЕЙСКИЙ,
Дата: 2018-12-21, просмотров: 974.