что даны две декартовы плоскости с осями x,y и u,v. Рассмотрим в этих плоскостях две замкнутые области: область (D) на плоскости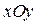 
и область 
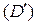на плоскости 
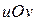. Каждая из этих областей может быть и неограниченной, в частности может охватывать и всю плоскость. Границу области (если область не охватывает всей плоскости) будем предполагать кусочно-гладкой кривой.
Допустим, что в области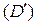 
дана система непрерывных функций
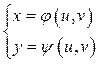, (1.5)
которая устанавливает между областями (D) и (D') взаимно однозначное соответствие. Задание пары значений переменных u и v из области (D') однозначно определяет некоторую точку в области (D) на плоскости xOy (и обратно). Это дает основание и числа u,v называть координатами точек области (D).
Кривую, составленную из точек области (D), у которых одна из координат сохраняет постоянное значение, называют координатной линией. В связи с тем, что координатные линии, вообще говоря, будут кривыми, числа u,v, характеризующие положение точки на плоскости xOy, и в этом случае (как и в случае кривой поверхности) называют криволинейными координатами точки.
Придавая координате u различные (возможные для нее) постоянные значения, получим семейство координатных линий на плоскости xOy. Фиксируя значение координаты v, получим другое семейство координатных линий. При наличии взаимно однозначного соответствия между рассматриваемыми областями различные линии одного и того же семейства не пересекаются между собой, и через любую точку области (D) проходит по одной линии из каждого семейства.
Вся сетка координатных линий на плоскости является изображе-нием сетки прямых u = const и v = const на плоскости 
(рис.1.13).
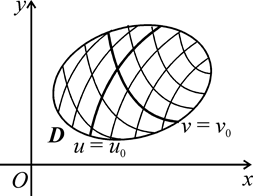
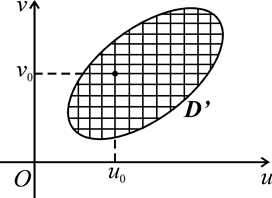
Рисунок 1.13
Далее будем предполагать, что функции (1.5) не только непрерывны, но и имеют непрерывные частные производные первого порядка.
Определение 5. Определитель второго порядка следующего вида
(1.6)
называют якобианом перехода от декартовых координат к криволинейным и обозначают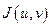 
.
Тогда формула перехода от декартовых координат к криволинейным координатам имеет следующий вид:
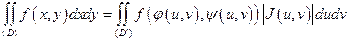, (1.7)
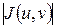≠ 0, за исключением конечного числа точек.
Замечание 3. На практике декартовы координаты точки и ее криволинейные координаты рассматривают не на разных координатных плоскостях, а на одной совмещенной.
Простейшим и важнейшим примером криволинейных координат являются полярные координаты 
. Они имеют наглядное геометрическое истолкование, как полярный радиус-вектор и полярный угол, но могут быть введены и формально, с помощью соотношений:
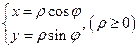. (1.8)
|
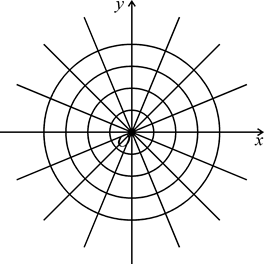
| Рисунок 1.14 |
Если значения ρ и φ откладывать по двум взаимно перпендикулярным осям, считая, скажем, ρ – абсциссой, а φ – ординатой (при правой ориентации осей), то каждой точке полуплоскости ρ≥0 по указанным формулам отвечает одна определенная точка на плоскости xOy.
Прямым ρ= const отвечают круги радиуса 
с центром в начале (полюсе), а прямым φ= const отвечают лучи, исходя-щие из начала (полюса) под углом φ к оси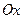 
(рис. 1.14).
Однако в данном случае формулы преобразования не будут однозначно разрешимы: изменения величины угл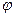а 
на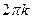 
(где k – целое) не отразится на значениях x и y. Для того чтобы получить все точки плоскости 
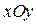, достаточно ограничиться значениями ρ ≥ 0, 0 ≤ φ < 2π. Каждой точке (x,y), отличной от начала, отвечает одно значение ρ > 0 и одно значение φ в указанных пределах. Но неустранимое нарушение однозначности соответствия связано с началом координат: точке x = y = 0 отвечает на плоскости 
вся ось 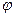(или, если угодно, отрезок ее от 
до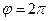 
).
Формулы (1.8) называют формулами связи между декартовыми и полярными координатами.
Используя формулу (1.6), вычисляем якобиан перехода от декартовых координат к полярным:
= 
= 
= 
.
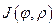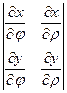Тогда, используя формулу (1.7), формула перехода от декартовых координат к полярным принимает следующий вид:
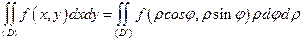. (1.9)
Определение 6. Область (D) называется правильной в направлении полярной оси , если луч, проходящий через внутренние точки области (D), пересекает границу области в двух точках (рис.1.15).
Рисунок 1.15
Следующая теорема позволяет вычислять двойной интеграл в полярных координатах (см. замечание 3).
ТЕОРЕМА 5. Если функция 
непрерывна в области (D), область (D) – правильная в направлении полярной оси ρ (рис. 1.15), то
.
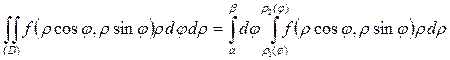Тогда по формуле (1.9) получаем:
.
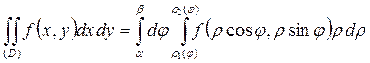ПРИМЕР 1. Вычислить интеграл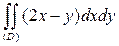 
, где (D) – параллело-грамм, ограниченный прямыми:
x + y = 1, x + y = 2, 2x – y = 1, 2x – y = 3. (*)
Решение
Изобразим область (D) на рисунке 1.16. Из рисунка видно, что для вычисления данного интеграла область (D) следует разбить на три части, как показано штриховыми линиями. Задача, таким образом, сводится к вычислению трех двойных интегралов. Однако можно избежать такого громоздкого способа решения, если ввести новые переменные, положив:
x + y = u, 2x – y = v. (**)
Тогда прямые x + y = 1, x + y = 2 в системе координат xOy преобразуются в прямые u = 1, u = 2 в системе координат uOv (рис. 1.17), а прямые 2x – y = 1, 2x – y = 3 преобразуются в прямые v = 1, v = 3. Параллелограмм (D) преобра-зуется в прямоугольник (Q) со сторонами, параллельными координатным осям.
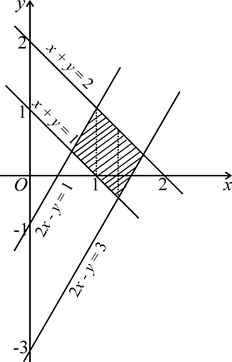
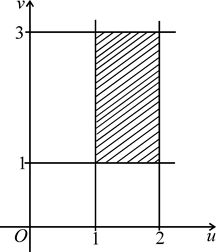
Рисунок 1.16 Рисунок 1.17
При преобразовании интеграла к новым переменным необходимо сначала получить выражения x и y через u и v из равенств (*) и (**):
x = 
, y =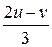 
.
Используя формулу (1.6), вычислим якобиан данного преобразования:
J(u,v) = 
= – 
– 
= – 
.
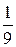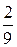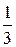Так как якобиан отличен от нуля, то выбранное преобразование области (D) в область (Q) будет взаимно однозначным. Кроме того, как функция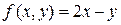 
, так и функции 
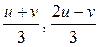вместе со своими частными производными являются непрерывными. Следовательно, по формуле (1.7) имеем:
Если подынтегральная функция или уравнение границы области интегрирования содержат сумму x2 + y2, то в большинстве случаев упрощение интеграла достигается преобразованием его к полярным координатам. Это объясняется тем, что данная сумма в полярных координатах получает весьма простое выражение
.
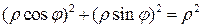Если в состав подынтегральной функции или уравнения границы области интегрирования входит сумма вида ax2 + by2; a > 0, b > 0, то пользуются «обобщенной» полярной системой координат:
.
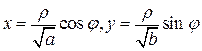Тогда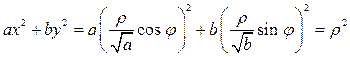 
,
а якобиан преобразования в этом случае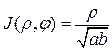 
(убедится самостоятельно).
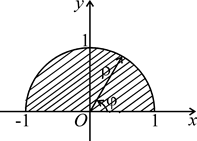
ПРИМЕР 2. Вычислить двойной интеграл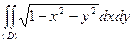 
, где (D) – верхний полукруг 
.
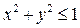Решение
Преобразуем интеграл к полярным координатам:
.
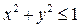Тогда
x2 + y2 = ρ2,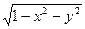 
= 
, 
,
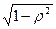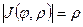и данный интеграл примет вид:
= 
.
|
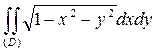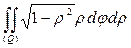| Рисунок 1.18 |
Рассмотрим область интегрирования (D) (рис. 1.18).
Уравнение ее границы в полярных координатах примет вид:
ρ2cos2φ + ρ2sin2φ = 1,
т.е. ρ2 = 1, или ρ = 1 (предполагается, что полярная ось совпадает с положительным направлением оси абсцисс). В пределах данной области (D) полярный угол φ изменяется от 0 до π, а полярный радиус ρ изменяется в пределах от 0 до 1.
Следовательно,
I = 
= 
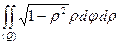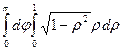= π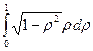 
=
= 
.
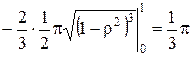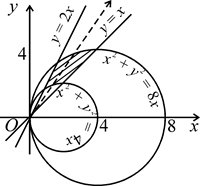
ПРИМЕР 3. Вычислить двойной интеграл I =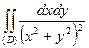 
, где область (D) ограничена окружностями x2 + y2 = 4x, x2 + y2 = 8x и прямыми y = x, y = 2x.
Решение
|
| Рисунок 1.19 |
Область (D) изображена на рисунке 1.19. Перейдем к полярным координатам x= ρ cos φ,
y = ρ sin φ. Тогда подынтегральная функция
f (x,y) =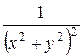 
= ρ-4.
Криволинейные участки границы области задаются уравнениями:
ρ2 cos2 φ + ρ2 sin2 φ = 4ρ cos φ, или ρ = 4 cos φ,
ρ2 cos2 φ + ρ2 sin2 φ = 8ρ cos φ, или ρ = 8 cos φ,
а прямолинейные участки уравнениями:
ρ sinφ = ρ cos φ, или tg φ = 1, откуда φ =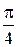 
;
ρ sin φ = 2ρ cos φ, или tg φ = 2, откуда φ = arctg 2;
Итак, угол φ изменяется в постоянных пределах от 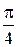до arctg 2. Чтобы найти пределы изменения ρ, пересечем область (D) лучом, исходящим из полюса. При входе в область он пересечет границу ρ = 4 cos φ, при выходе – границу ρ = 8 cos φ. Следовательно, 4 cos φ – нижняя граница интегриро-вания, а 8 cos φ – верхняя граница.
Имея в виду, что при данном преобразовании якобиан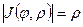 
, можем представить двойной интеграл в новых координатах следующим образом:
I =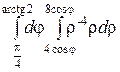 
= 
= 
=
= 
= 
= 
.
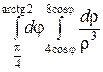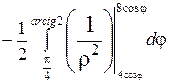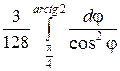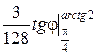ПРИМЕР 4. При какой замене переменных криволинейный четырех-угольник (D), ограниченный линиями xy = 1, xy = 2, x – y + 1 = 0, x – y – 1 = 0 (x > 0, y > 0), перейдет в прямоугольник (Q), стороны которого параллельны координатным осям?
Решение
Криволинейный четырехугольник (D) изображен на рисунке 1.20. Обозначим новые переменные через u и v. В системе координат uOv по условию задачи прямоугольник(Q) должен быть ограничен некоторыми прямыми, параллельными координатным осям, u = u1, u = u2, v = v1, v = v2. Из уравнений заданных линий
xy = 1, x – y = –1,
xy = 2, x – y = 1
видно, что при xy = u, x – y = v получится требуемое преобразование. Прямо-угольник (Q) будет ограничен прямыми u = 1, u = 2, v = –1, v = 1 (рис. 1.21).
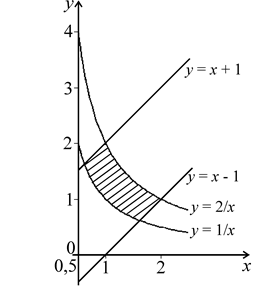
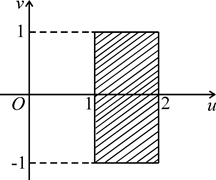
Рисунок 1.20 Рисунок 1.21
Дата: 2018-12-21, просмотров: 593.
