Определение 4. Область 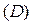 называется правильной в направлении оси ординат, если любая прямая, проходящая через внутренние точки области
называется правильной в направлении оси ординат, если любая прямая, проходящая через внутренние точки области 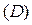 параллельно оси ординат, пересекает границу этой области в двух точках.
параллельно оси ординат, пересекает границу этой области в двух точках.
Аналогично дается определение области, правильной в направлении оси абсцисс.
Следующие две теоремы позволяют вычислять двойные интегралы в декартовых координатах.
ТЕОРЕМА 3. Если функция 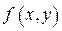 непрерывна в области
непрерывна в области 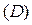 , область
, область  - правильная в направлении оси ординат (рис. 1.4), то
- правильная в направлении оси ординат (рис. 1.4), то
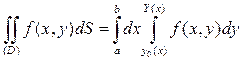 .
.
|
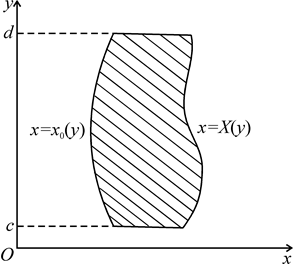
| Рисунок 1.5 |
ТЕОРЕМА 4. Если функция 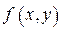 непрерывна в области
непрерывна в области 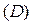 , область
, область 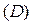 – правильная в направлении оси абсцисс (рис. 1.5), то
– правильная в направлении оси абсцисс (рис. 1.5), то
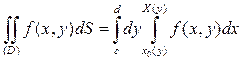 .
.
ПРИМЕР 1. Записать двойной интеграл 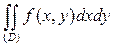 в виде
в виде
повторных интегралов (двумя способами), если:
а) область 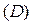 ограничена прямыми x = 1, x = 2, y = 0, y = 4.
ограничена прямыми x = 1, x = 2, y = 0, y = 4.
Решение
Построив на чертеже прямые, ограничивающие область интегриро-вания, видим, что 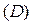 представляет собой прямоугольник, стороны которого параллельны координатным осям (рис.1.6). В этом случае обе переменные
представляет собой прямоугольник, стороны которого параллельны координатным осям (рис.1.6). В этом случае обе переменные 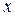 и
и 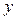 изменяются в постоянных пределах
изменяются в постоянных пределах 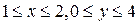 , а формулы для вычисления двойного интеграла принимают соответственно вид:
, а формулы для вычисления двойного интеграла принимают соответственно вид:
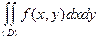 =
= 
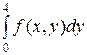 ;
; 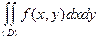 =
= 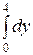
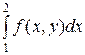 .
.
б) область 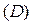 ограничена линиями x = 0, x2 + y2 = r2, причем x ≥ 0, r > 0.
ограничена линиями x = 0, x2 + y2 = r2, причем x ≥ 0, r > 0.
Решение
Изобразим область интегрирования 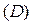 на чертеже (рис.1.7).
на чертеже (рис.1.7).
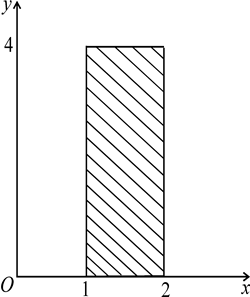
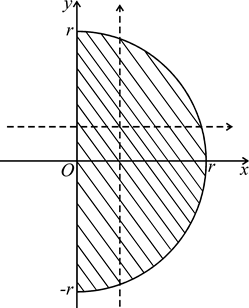
Рисунок 1.6 Рисунок 1.7
Возьмем сначала постоянные пределы по переменной 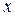 . Ими будут числа
. Ими будут числа 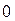 и
и 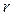 . Для каждого значения
. Для каждого значения 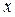 из отрезка
из отрезка 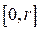
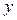 принимает значения от
принимает значения от 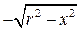 до
до 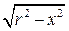 .
.
Получим:
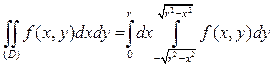 .
.
Если постоянные пределы взять по 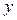
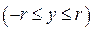 , то
, то 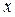 принимает значения от
принимает значения от 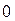 до
до 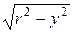 .
.
Получим:
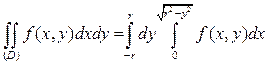 .
.
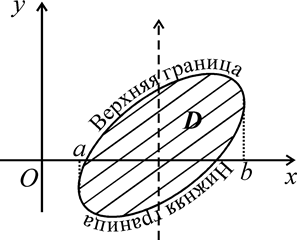
Вообще при определении переменных пределов интегрирования полезно пользоваться следующим правилом: пусть 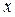 изменяется в постоянных пределах
изменяется в постоянных пределах 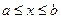 (рис.1.8). Чтобы получить пределы интегрирования по
(рис.1.8). Чтобы получить пределы интегрирования по 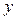 , пересечем область
, пересечем область  лучом, параллельным и одинаково направленным с осью ординат. Граница области, которую луч пересечет при входе в область, будет нижней границей этой области, а ее уравнение, решенное относительно
лучом, параллельным и одинаково направленным с осью ординат. Граница области, которую луч пересечет при входе в область, будет нижней границей этой области, а ее уравнение, решенное относительно 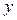 , служит для установления нижнего
, служит для установления нижнего
|
| Рисунок 1.8 |
предела интегрирования по y
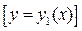 .
.
Граница области, которую луч пересекает, выходя из области, будет верхней границей этой области, а ее уравнение, решенное относительно 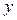 , служит для установления верхнего предела интегрирования по y
, служит для установления верхнего предела интегрирования по y
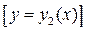 .
.
Аналогичным образом при постоянных пределах по y определя-ются переменные пределы по x.
ПРИМЕР 2. Записать двойной интеграл 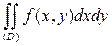 в виде повторных интегралов (двумя способами), если область
в виде повторных интегралов (двумя способами), если область 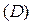 – квадрат, ограниченный прямыми
– квадрат, ограниченный прямыми 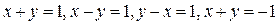 .
.
Решение
|
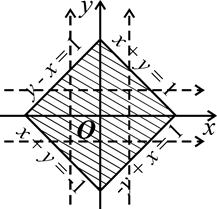
| Рисунок 1.9 |
Строим на чертеже область интегрирования 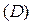 (рис.1.9). Пусть постоянны пределы интегрирования по x. Ими будут –1 и +1. Проведем через область (D) луч, параллельный и одинаково направленный с осью Oy. Как нижняя, так и верхняя границы области состоят из двух отрезков, пересекающихся соответственно в точках (0,–1) и (0,1).
(рис.1.9). Пусть постоянны пределы интегрирования по x. Ими будут –1 и +1. Проведем через область (D) луч, параллельный и одинаково направленный с осью Oy. Как нижняя, так и верхняя границы области состоят из двух отрезков, пересекающихся соответственно в точках (0,–1) и (0,1).
Поэтому разобьем область 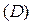 на две части прямой
на две части прямой 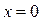 . Тогда получим:
. Тогда получим:
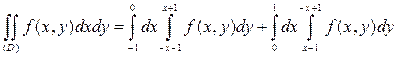 .
.
Аналогично при выборе постоянных пределов по у получим:
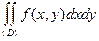 =
= 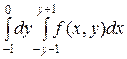 +
+ 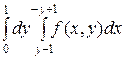 .
.
ПРИМЕР 3. Изменить порядок интегрирования в повторном интеграле
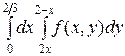 .
.
Решение
Решение данной задачи состоит из двух частей:
а) восстановить область интегрирования (D) по известным пределам данного повторного интеграла;
б) записать повторный интеграл с постоянными пределами по y и переменными по x.
|
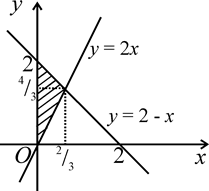
| Рисунок 1.10 |
Так как внутренний интеграл взят по y, то, следовательно, пределы внутреннего интеграла получены из уравнений y = 2x и y = 2 – x. Это уравнения прямых, которые составляют какую-то часть границы области интегрирования (D). Изобразим прямые на чертеже (рис.1.10). Решая совместно уравнения y = 2x и y = 2 – x, найдем точку пересечения этих прямых 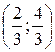 . Так как дано, что абсцисса x точек области (D) изменяется в пределах от 0 до
. Так как дано, что абсцисса x точек области (D) изменяется в пределах от 0 до 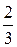 , то можно заключить, что искомой областью (D) является фигура, ограниченная линиями x = 0, y = 2x и y = 2 – x.
, то можно заключить, что искомой областью (D) является фигура, ограниченная линиями x = 0, y = 2x и y = 2 – x.
Расставляя теперь внешние пределы интегрирования по y, а внутренние по x, получаем:
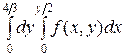 +
+ 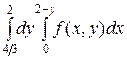 .
.
ПРИМЕР 4. Изменить порядок интегрирования
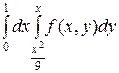 +
+ 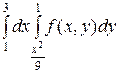 .
.
Решение
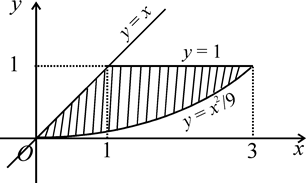
а) Восстановим область интегрирования (D). Рассматривая оба слагаемых одновременно, заключаем, что нижний предел внутреннего интеграла на участках 0 ≤ х ≤ 1 и 1 ≤ х ≤ 3 выражается через x одинаково: (парабола). Верхним же пределом на участке 0 ≤ х ≤ 1 является прямая y = x, а на участке 1 ≤ х ≤ 3 – прямая y = 1. Этого достаточно, чтобы построить область (D) (рис. 1.11).
|
| Рисунок 1.11 |
б) Из чертежа (см. рис. 1.11) видно, что постоянными пределами по y являются числа 0 и 1. Нижним пределом изменения x будет x = y, а верхним – x = 3 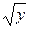 .
.
Корень берем с положитель-ным знаком потому, что все точки области (D) имеют неотрицательные абсциссы. Искомый повторный интеграл представится в виде
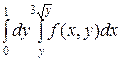
ПРИМЕР 5. Вычислить двойной интеграл I = 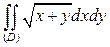 , где область (D) ограничена прямыми x = 0, y = 0, x + y = 1.
, где область (D) ограничена прямыми x = 0, y = 0, x + y = 1.
Решение
|
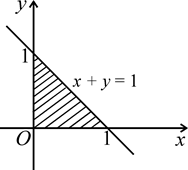
| Рисунок 1.12 |
Область (D) изображена на рисунке 1.12.
Возьмем постоянные пределы по переменной x, 0 ≤ х ≤ 1 . Тогда по y нижним пределом будет y = 0, а верхним y = 1 – x. Получим:
I = 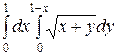 =
= 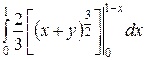 =
=
= 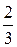
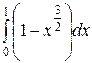 =
= 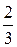
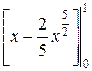 =
= 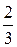
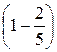 =
= 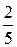 .
.
Дата: 2018-12-21, просмотров: 388.