Возьмем произвольную фигуру 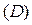 на плоскости, представляющую собой ограниченную и замкнутую область. Ее границу мы всегда будем представлять в виде замкнутой кривой (или нескольких таких кривых).

Определение 2. Область 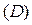 называется квадрируемой, если она имеет площадь.

Замечание 1. В дальнейшем будем рассматривать только квадрируемые области.

Пусть в области 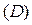 определена функция двух переменных 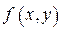. Разобьем область  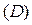сетью кривых на конечное число элементарных областей  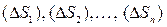соответственно с площадями 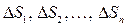. В каждой элементарной области  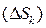возьмем по произвольной точке 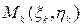, значение функции в этой точке  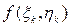умножим на площадь  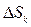соответствующей области, и все подобные произведения сложим. Полученную сумму

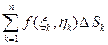                                         (1.3)

будем называть интегральной суммой для функции f ( x , y ) по области (D).

Обозначим через 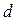 наибольший из диаметров  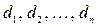элементарных областей .

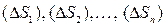Определение 3. Если при стремлении к нулю наибольшего из диаметров 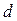 существует конечный предел  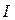интегральной суммы (1.3), и он не зависит ни от способа разбиения области  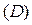на элементарные области 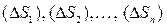, ни от выбора точек  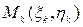в каждой элементарной области 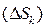, то этот предел называется двойным интегралом от функции  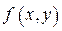по области  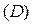и обозначается .

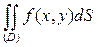Теорема 1. (необходимое условие существования двойного интеграла). Если функция 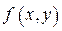 интегрируема в ограниченной замкнутой области 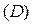, то она ограничена в этой области.

Теорема 2. (достаточное условие существования двойного интеграла). Если функция 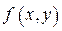 непрерывна в ограниченной замкнутой области 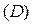, то она интегрируема в ней.

Из пункта 1.1. следует геометрический смысл двойного интеграла. Если функция 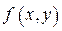 неотрицательна: 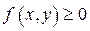– и интегрируема в области 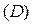, то двойной интеграл от функции  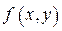по области  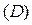равен объему тела, сверху ограниченного поверхностью  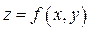, c боков – цилиндрической поверхностью с образующими, параллельными оси 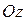, снизу – областью  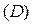на плоскости : .

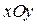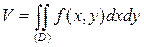Свойства двойного интеграла

1. .

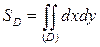2. Если функцию 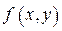, интегрируемую в области 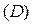, умножить на постоянную k, то полученная функция k f (x,y) также будет интегрируема в области 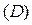, причем

.

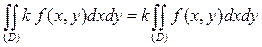3. Если в области 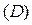 интегрируемы функци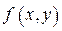и  и 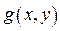, то интегрируема и функция 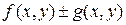, причем

.

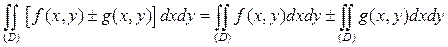4. Если область 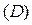, в которой задана функция 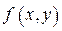, кривой  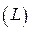разделена на две област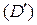и  и 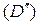, то из интегрируемости функции  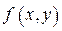во всей области  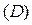следует ее интегрируемость в областях  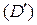и 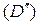, и обратно – из интегрируемости функции в обеих областях  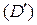и 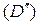 вытекает ее интегрируемость в области 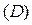. При этом

.

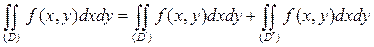5. Если для интегрируемых в области 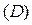 функци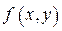й  и 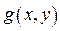 выполняется неравенств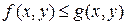о , то .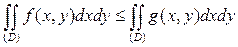

6. В случае интегрируемости функции 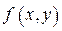 в области  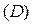интегрируема и функция |f(x,y)| в области 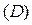, и имеет место неравенство .

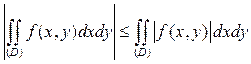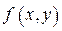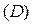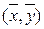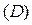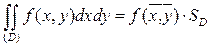
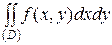7. Теорема О СРЕДНЕМ. Если функция  непрерывна в области , то найдется такая точка  в области , что  = f 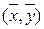·S_D, где S_D – площадь области D.

Замечание 2. Свойство 3 обобщается на любое конечное число функций. Свойство 4 обобщается на любое конечное число областей.