Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

Будем рассматривать систему диофантовых уравнений

 

a₁₁*x₁ +a₁₂ *x₂ +…+a_1n *x_n = c₁                           

a₂₁*x₁ +a₂₂ *x₂ +…+a_2n *x_n = c₂                                                                (9) 

…

a_m1*x₁ +a_m2 *x₂ +…+a_mn *x_n = c_m                         

 

       Рассмотрим сначала метод исключения для решения данной системы.

       Из первого уравнения можно найти все неизвестные в виде (8).

 

x₁ = g₁₁  * t₁ + g₁₂ t₂ + … + g_1(n-1) * t_n-1           

…                                                                                      

x_n = g_n1  * t₁ + g_n2 t₂ + … + g_n(n-1) * t_n-1 

 

 где  t₁ , t₂ , … t_n-1 пробегают множество целых чисел Z .

       Подставим полученные решения в последние (m-1) уравнений и получим систему из (m-1) уравнений с (n-1) переменными.

       Далее действуем аналогично, пока не придем к задаче решения одного диофантова уравнения. Находим его решение в виде (8).

       Решения последнего уравнения подставляем в общее решение предпоследнего. И предпоследнего – в предыдущее, и т.д., пока не получим решение исходного уравнения. 

 

Сложность данного алгоритма имеет порядок O(m²*n²).

 

Теорема 2. (см. [56, стр. 16]). Пусть система независимых линейных уравнений (9) c целыми коэффициентами  a_ij и целой правой частью c_i , i = 1, …,m , j = 1, …, n , имеет ранг m. Эта система имеет целочисленные решения x_j , j = 1, …, n, тогда и только тогда, когда наибольший общий делитель всех миноров m-го порядка основной матрицы делится на наибольший общий делитель всех миноров m-го порядка расширенной матрицы. 

 

Теорема 3. (см. [56, стр. 16]) Пусть A = { a_ij }, i = 1, …,m , j = 1, …, n – целочисленная матрица ранга m . Тогда существует такая целочисленная унимодулярная (определитель которой равен +1 или -1) матрица V = {v_kj }_n*n , что матрица H=A*V является эрмитовой формой матрицы A – то есть имеет вид: 

 

 h₁₁ 0 0 …          0  

 h₂₁ h₂₂ 0 …          0 

 …         

 h_m1 h_m2      h_mm … 0 

          

где все h_ij целые и h_ii ≠ 0 , i = 1, …,m , j = 1, …, n.

       Доказательство теоремы содержит алгоритм (т.е. доказательство конструктивно), называемый алгоритмом Эрмита. Матрица A будет приводиться к матрице H с помощью элементарных столбцовых преобразований двух видов: перестановки столбцов; прибавления к одному столбцу другого, умноженного на число. Всякое такое элементарное преобразование сводится к умножению исходной матрицы справа на соответствующую элементарную матрицу. Элементарные матрицы, соответствующие данным двум элементарным преобразованиям, являются унимодулярными.

       Алгоритм имеет на входе матрицу A, которая элементарными преобразованиями столбцов преобразуется в матрицу H. При этом матрица V будет представлена как произведение элементарных матриц, соответствующих элементарным преобразованиям столбцов. Алгоритм состоит из m шагов. На k-ом шаге алгоритма строится k-ая строка матрицы H.

       k-ый шаг алгоритма.

       Проверка окончания k-ого шага. Если a_kk ≠ 0, а все элементы a_kj =0, j = k+1, …, n , то k-ый шаг завершен и переход к шагу k+1. Иначе

       Перестановкой столбцов с номерами k, …, n на место (k, k) ставим наименьший по модулю ненулевой элемент из элементов a_kj, j = k, …, n .

       Элементарными столбцовыми преобразованиями второго типа делаем элементы a_kj, j = k+1, …, n, меньшими элемента a_kk . Эти преобразования имеют вид:

 

                   a_kj = a_kj – a_kk*[a_kj/a_kk] ,     j = k+1, …, n

 

Здесь [x] – наименьшее целое число, не превосходящее x.     

Переход на проверку окончания k-ого шага. 

Поскольку каждое повторение k-ого шага уменьшает модуль a_kk на целое число, данный процесс завершится.

       Конец доказательства.

 

О сводимости сравнений к диофантовым уравнениям.

 

Пусть p – некоторое число. Два числа a и b называют сравнимыми по модулю p, если разность этих чисел делится нацело на p. Отношение сравнения записывают следующим образом: a ≡ b mod p. 

Пусть F(x₁,x₂,…,x_n) – целочисленная линейная функция от целых аргументов (x₁,x₂,…,x_n). Рассмотрим задачу нахождения всех значений переменных (x₁,x₂,…,x_n), для которых выполняется сравнение  

 

F(x₁,x₂,…,x_n) ≡ 0 mod p                                                                     (10)  

 

Определение сравнения означает, что существует такое целое число k, для которого  

F(x₁,x₂,…,x_n) = k*p   

 

Решив это диофантово уравнение, получим решение сравнения (10).  

 

Сведения из теории графов

 

В этом параграфе кратко приводятся сведения из теории графов, необходимые для изложения основного материала. Более подробно теорию графов можно изучать по книгам [47], [85], [92], [93].

 

Графы и их изоморфизмы

 

Граф – это множество точек, называемых вершинами, и отрезков, называемых ребрами, которые эти вершины соединяют. Обозначают граф G(X,U), где G – это имя графа, X – множество вершин, U – множество ребер (x_1, x₂), x_1, x₂ Î X .

       Графы различают ориентированные и неориентированные. По умолчанию граф предполагается неориентированным. Для неориентированных графов отождествляются пары (x_1, x₂) и (x_2, x₁). Для ориентированных графов пары (x_1, x₂) и (x_2, x₁) различаются и, как правило, называются дугами (а не ребрами).             

       Вершины x_1, x₂ называются концевыми или инцидентными к ребру (дуге)   (x_1, x₂) . Эти же вершины называются смежными друг к другу. 

Изоморфизм графов G(X,U) и H(Y,V) – это такое биективное отображение множества X на множество Y, при котором смежные вершины переходят в смежные, а несмежные – в несмежные.

 

Пример 1. На следующем рисунке первый граф изоморфен второму и неизоморфен третьему.

 

 

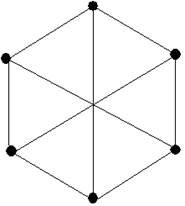
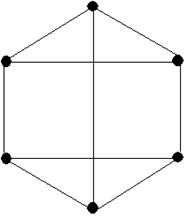
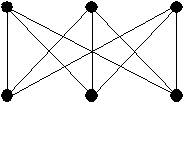
       Рис. 1. Первый граф изоморфен второму и неизоморфен третьему.

 

Два графа называются изоморфными, если существует изоморфизм одного из этих графов на другой. Ясно, что изоморфизм устанавливает на множестве графов отношение эквивалентности.

Автоморфизм графа – это изоморфизм графа на самого себя. Суперпозиция автоморфизмов – опять автоморфизм. Множество автоморфизмов графа с операцией суперпозиции образуют группу, которая называется группой автоморфизмов графа.

       Пока не найден алгоритм полиномиальной сложности для проверки изоморфности двух графов. Вопрос о существовании такого алгоритма составляет «Проблему изоморфизма».

 

Степени вершин и связность

 

       Степень вершины – это количество ребер, инцидентных данной вершине.  

       Имеет место следующий факт (иногда называемый леммой о рукопожатиях): сумма степеней всех вершин графа равна удвоенному количеству всех ребер. Или, в виде формулы:

 

       ∑_{x Î X} ρ(x) = 2*|U|                            

 

где X – множество вершин, ρ(x) – степень вершины x, U – множество ребер, |U| - количество элементов множества U.          

       Вершина, степень которой равна единице, называется висячей.

       Если в ориентированном графе есть дуга (x_1, x₂), то говорят, что эта дуга выходит из вершины x₁ и входит в вершину x₂ . 

       Количество дуг, выходящих из вершины x, называется полустепенью исхода, а количество дуг, входящих в вершину x, – полустепенью захода.

       Очевидно, сумма полустепеней исхода всех вершин ориентированного графа равна сумме полустепеней захода всех вершин.  

       Источник – это вершина в ориентированном графе, в которую не входит ни одна дуга.

Сток – это вершина в ориентированном графе, из которой не выходит ни одна дуга.

Граф называется однородным, если степени всех его вершин равны.

 

       Неориентированный граф называется связным, если для любых двух вершин графа существует путь, для которого эти вершины являются начальной и конечной.

       Путь в неориентированном графе – это такая чередующаяся последовательность вершин и ребер, что для каждого ребра в последовательности соседние с ним вершины – это обе концевые вершины данного ребра.     

       Цикл в неориентированном графе – это путь, у которого начальная и конечная вершины совпадают.

       Путь в ориентированном графе – это такая последовательность вершин, что в каждую вершину этой последовательности (кроме первой) входит дуга из предыдущей вершины.  

       Длина пути – это количество ребер на этом пути.

       Расстояние между вершинами – это длина кратчайшего пути.

       Диаметр графа – это наибольшее расстояние между парами вершин графа.

       Контур в ориентированном графе (ориентированный цикл) – это ориентированный путь, у которого начальная и конечная вершины совпадают.

       Сильно связный ориентированный граф – это ориентированный граф, в котором для любых двух вершин существует путь из первой вершины во вторую и существует путь из второй вершины в первую. Равносильное определение: ориентированный граф является сильно связным, если любые две вершины принадлежат некоторому контуру.

 

Деревья

 

Дерево – это связный неориентированный граф без циклов.

В любом дереве всегда существует хотя бы одна висячая вершина.

Существует большой список характеристических свойств дерева.

 

       Теорема 4 ([93]). Следующие условия эквивалентны.

1. Граф G(X,U) – дерево.
2. Любые две вершины в графе G(X,U) соединены единственным простым путем.
3. Граф G(X,U) связный, и |X| = |U| +1.
4. Граф G(X,U) не содержит циклов, и |X| = |U| +1.
5. Добавление любого ребра к графу G(X,U) создает ровно один цикл.