Общие вопросы и определения. Законы коммутации. Изменение режима работы электрической цепи в результате включения и отключения цепи или изменение ее параметров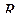 
, 
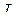и 
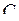называется коммутацией. Процессы, происходящие в цепи в результате коммутации, называются переходными.
Переходные процессы возникают в цепях, содержащих элементы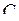 
и 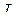. Они обладают способностью накапливать и отдавать энергию соответственно магнитного и электрического полей.
Изменение энергии не может происходить мгновенно. Энергия магнитного поля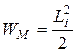 
, электрического поля 
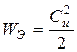. Для изменения энергии поля на конечное значение необходимо некоторое время, так как внезапное, скачкообразное изменение энергии 
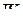равносильно тому, что мощность источника 
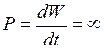, что физически невозможно. На этом основаны два закона коммутации.
Первый закон коммутации. Ток в ветви с индуктивностью не. может изменяться скачком:
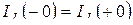(5.1)
Второй закон коммуникации. Напряжение на емкости не может изменяться скачком:
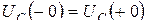(5.2)
Законы Кирхгофа справедливы как по отношению к установившимся, так и к неустановившимся режимам. Анализ переходных процессов в электрической цепи производится путем решения дифференциальных уравнений, составленных по законам Кирхгофа.
Включение цели и на постоянное напряжение. Для цепи, изображенной на рис. 5.1, по второму закону Кирхгофа имеем уравнение
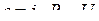
подставив значение ЭДС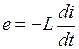 
, получим дифференциальное уравнение
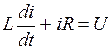(5.4)
Ток в цепи во время переходного режима
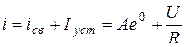(5.5)
Значение постоянной интегрирования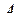 
:
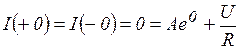
отсюда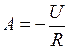 
(5.6)
Действительный ток в цепи в переходном процессе
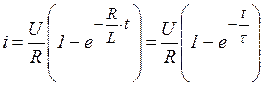(5.7)
На рис. 5.2 изображена кривая изменения тока в рассматриваемой цепи. Скорость протекания переходного процесса определяется постоянной времени цепи
 |
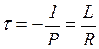(5.8)
Рис. 5.2
Постоянная времени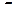 
графически определяется длиной касательной 
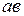(рис. 5.2) и кривой 
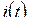. Значения тока 
в цепи различных моментов времени определяются из формулы (5.7) и приведены в таблице 5.1
Таблица 5.1
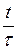
| 1 | 2 | 3 | 4 |
|
|
|
|
|
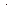
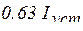
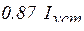
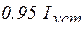
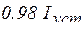
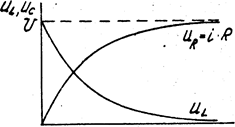
(рис. 5.5)
Напряжение на индуктивном элементе в переходный период (рис. 5.3)
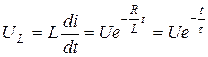(5.9)
Характер изменения величин в цепях с одним накопителем энергии подчиняется экспоненциальному закону. Таким образом, задача сводится к определению конкретных значений начальных и остановившихся токов и напряжений.
Пример 5.1. По какому закону будут изменяться токи ,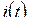 
, 
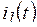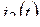и напряжение 
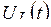цепи на рис. 5.4 при переходном процессе, вызванном замыканием рубильника?
Решение сводится к определению начальных и установившихся значений токов и напряжений. Так как ток в катушке индуктивности скачком изменяться не может (см. формулу (5.2)), схема для определения начальных значений величин примет вид, изображенный на рис. 5.5, где
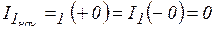
Остальные токи, напряжения в схеме определяются как обычно для цепей постоянного тока: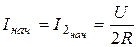 
; 
; 
;
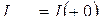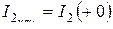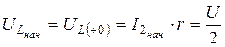
Схема на рис. 5.6 для установившегося режима получена при 
, а 
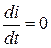и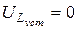 
Рис.5.4 Рис. 5.5 Рис. 5.6
Кривые изменения токов и напряжений изображены на рис. 5.7 и рис. 5.8.
Отключение цепи с 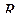и 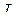от источника постоянного напряжения. При отключении индуктивной катушки от источника (рис.5.9) ток в ней 
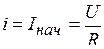в первый момент времени остается неизменным, зато в резисторе 
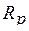ток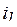 
меняется скачком от нудя до - 
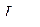(знак минус показывает, что он направлен против указанного на схеме положительного направления). Для уменьшения потерь в цепи при включенной катушке последовательно с разрядным сопротивление включен диод Д, благодаря чему ток 
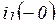до размыкания выключателя равен нулю.
Согласно второму закону Кирхгофа,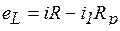 
; так как 
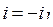, то
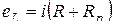или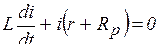 
Отсутствие правой части в уравнении означает, что ток в переходном процессе равен свободной составляющей (энергия извне не поступает)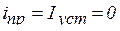 
Ток в цепи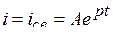 
Поскольку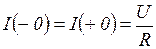 
, то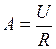 
.
Таким образом,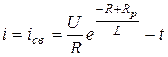 
ток в разрядном сопротивлении 
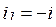(рис. 5.10).
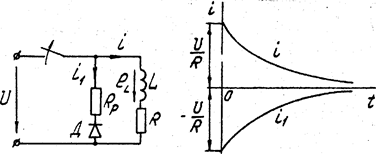
Рис. 5.9 Рис. 5.10
Включение цепи с 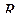и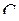 
на постоянное напряжение. Для цепи (рис. 5.11) по второму закону Кирхгофа 
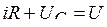; так как 
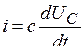, получаем уравнение
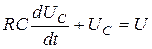
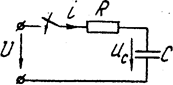
Рис. 5.11
Напряжение на конденсаторе в процессе заряда (рис. 5.12)
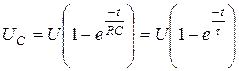(5.14)
Ток в цепи заряда конденсатора
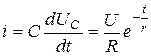(5.15)
где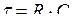 
.
Пример 5.2. Определить начальные и установившиеся значения токов , 
, 
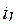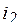, и напряжений 
, 
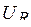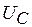в цепи, изображенной на рис. 5.13, при замыкании ключа.
Решение. Схема для определения начальных стечении величин при 
изображена на рис. 5.14, где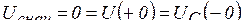 
,
, 
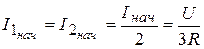
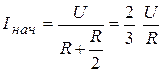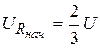
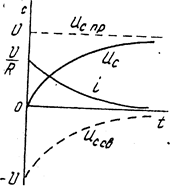
Рис. 5.12
Схема для определения установившихся значений величин при 
приведена не рис. 5.15.
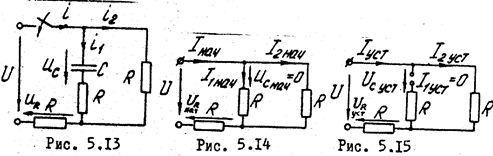
Известно, что постоянный ток через емкость в установившемся процессе не проходит: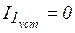 
, 
, 
, 
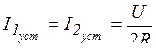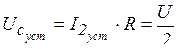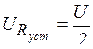
Разряд конденсатора на сопротивление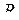 
. Уравнение для цепи (рис. 5.16), составленное по второму закону Кирхгофа, имеет вид 
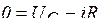, где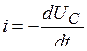 
- знак минус означает, что направление тока при разряде конденсатора не совпадает с положительным направлением напряжения 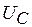. В конце процесса 
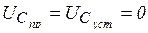. Поэтому 
, 
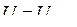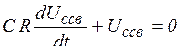
Решение этого уравнения имеет вид
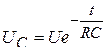
а ток разряда
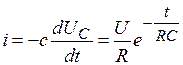
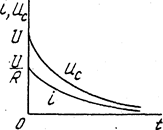
Рис. 5.17
Графики изображены на рис. 5.17.
Вопросы для самопроверки
1. Почему ток в цепи с индуктивной катушкой не может измениться скачком?
2. Могут ли напряжения на конденсаторе и ток через конденсатор меняться скачком?
3. Что такое постоянная времени электрической цепи?
4. 0т чего зависит быстрота окончания Рис. 5.17 переходного процесса (в цепи с 
и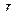 
, в цепи с и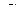 
)?
5. В каких цепях при коммутации переходный процесс отсутствует?
6. Назовите причины возникновения переходных процессов в электрических цепях.
7. Как определить постоянную времени по графику?.
Дата: 2018-12-21, просмотров: 463.
