Рис. 3.24 Рис. 3.25
В нем 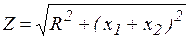 - полное сопротивление цепи последовательно соединенных элементов;
- полное сопротивление цепи последовательно соединенных элементов;  - угол сдвига по фазе между током и напряжением этой цепи, определяемый из
- угол сдвига по фазе между током и напряжением этой цепи, определяемый из  сопротивлений:
сопротивлений:
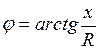

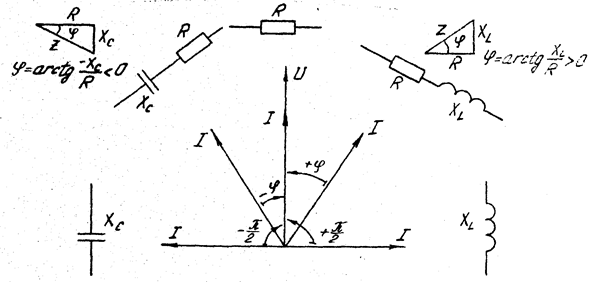
Рис. 3.26
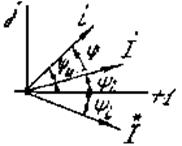
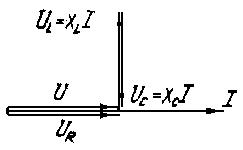
Угол  на векторной диаграмме отсчитывается от вектора тока к вектору напряжения. При этом
на векторной диаграмме отсчитывается от вектора тока к вектору напряжения. При этом  , если отсчет идет против часовой стрелки, и
, если отсчет идет против часовой стрелки, и  , если наоборот (рис. 3.26).
, если наоборот (рис. 3.26).
Закон Ома для цепи переменного тока: 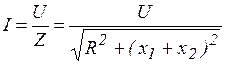
 Если стороны
Если стороны  напряжении умножить на общий
напряжении умножить на общий
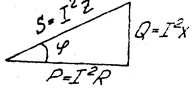
ток I , получим треугольник мощностей (рис. 3.27)
в нем:
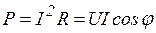 - активная мощность Вт;
- активная мощность Вт;
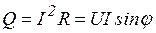 Рис. 3.27
Рис. 3.27
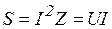 - полная мощность цепи,
- полная мощность цепи, 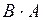 . Из
. Из 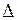 мощностей
мощностей 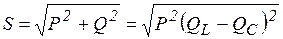 . Полная мощность цепи
. Полная мощность цепи 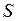 (участка цепи) измеряется с помощью амперметра и вольтметра, активная мощность
(участка цепи) измеряется с помощью амперметра и вольтметра, активная мощность 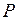 - с помощью ваттметра. Реактивная мощность
- с помощью ваттметра. Реактивная мощность 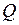 правило, вычисляется через найденные
правило, вычисляется через найденные  и
и  :
: 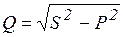 . Схема для измерения полной мощности
. Схема для измерения полной мощности 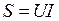 и активной мощности
и активной мощности 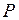 потребителя представлена на рис. 3.28.
потребителя представлена на рис. 3.28.
Рис. 3.28
Пример 3.2. Определить активную, реактивною и полную мощность 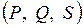 , для вышеуказанной цепи, а также эквивалентные пара метры потребители
, для вышеуказанной цепи, а также эквивалентные пара метры потребители 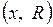 , если показание ваттметра 300 Вт, вольтметра 100 В, амперметра 5 А.
, если показание ваттметра 300 Вт, вольтметра 100 В, амперметра 5 А.
Решение. I) Ваттметр измеряет активную мощность потребителя, следовательно, Р = 300 Вт.
2) Вольтметр и амперметр фиксируют действующие значения напряжения U и тока I потребителя. Следовательно, полная мощность
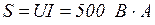
3) Из  мощностей потребителя (рис. 3.39) определяется реактивная мощность
мощностей потребителя (рис. 3.39) определяется реактивная мощность
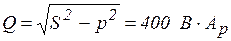
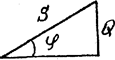
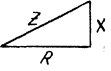
Рис. 3.29 Рис. 3.30
4) Полное сопротивление потребителя 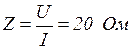
5) Активное сопротивление 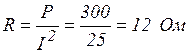
6) Реактивное сопротивление из 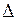 сопротивлений потребителя (рис. 3.30):
сопротивлений потребителя (рис. 3.30):
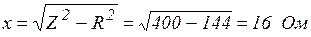
Примечание. 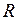 и
и 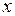 потребителя можно определить, используя выражения для мощностей
потребителя можно определить, используя выражения для мощностей 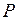 и
и 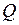 потребителя:
потребителя: 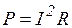 и
и 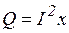
Применение комплексных чисел в расчете допей переменного тока. Данный метод позволяет заменить геометрические операции с векторами алгебраическими операциями с комплексными числами, соответствующими этим векторам. Представим синусоидальный ток 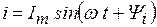 вращающимися векторами на декартовой плоскости, после чего формально совместим оси абсцисс и ординат соответственно с осями действительных и мнимых чисел комплексной плоскости (рис. 3.31). Тогда синусоидальный ток можно представить комплексным числом - точкой на комплексной плоскости, в которой лежит конец вектора I . Это комплексное число может быть выражено одной из следующих форм:
вращающимися векторами на декартовой плоскости, после чего формально совместим оси абсцисс и ординат соответственно с осями действительных и мнимых чисел комплексной плоскости (рис. 3.31). Тогда синусоидальный ток можно представить комплексным числом - точкой на комплексной плоскости, в которой лежит конец вектора I . Это комплексное число может быть выражено одной из следующих форм:
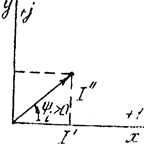
Рис. 3.31
а) алгебраической 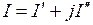
б) тригонометрической 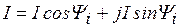
в) показательной 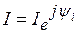 , где
, где 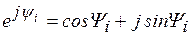 . В этих выражениях
. В этих выражениях 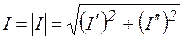
 - начальная фаза тока, которая отсчитывается от положительного направления оси действительных чисел к вектору;
- начальная фаза тока, которая отсчитывается от положительного направления оси действительных чисел к вектору;  , если отсчет против часовой стрелки и
, если отсчет против часовой стрелки и 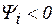 , если наоборот;
, если наоборот;
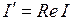 - действительная часть комплексного числа I;
- действительная часть комплексного числа I;
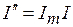 - мнимая часть комплексного числа I (точнее
- мнимая часть комплексного числа I (точнее 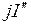 );
);
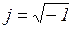 - мнимая единица;
- мнимая единица;
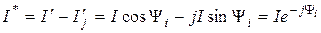 комплексное число, сопряженное с I;
комплексное число, сопряженное с I;
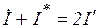 - действительное число;
- действительное число;
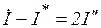 - мнимое число;
- мнимое число;
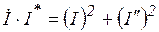 - квадрат модуля - действительное число.
- квадрат модуля - действительное число.
Пример 3.3. Напряжение 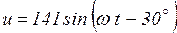 представить комплексным числом, записанным в формах а), б), в) и вектором на комплексной плоскости.
представить комплексным числом, записанным в формах а), б), в) и вектором на комплексной плоскости.
В показательной форме записи комплекс действующего значения напряжения 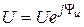 , где действующее напряжения
, где действующее напряжения 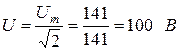 ,d начальная фаза
,d начальная фаза 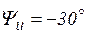 .
.
Ответ: алгебраическая 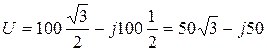 ;
;
тригонометрическая 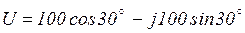 ;
;
показательная форма записи 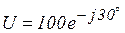 .
.
Векторное изображение напряжения см. на рис. 3.32.
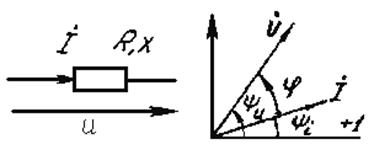
Примем без доказательства каждому линейному соотношению между векторами соответствует такое же соотношение между комплексными числами, соответствующими этим векторам. Так для I закона Кирхгофа в цепи переменного тока (рис. 3.33) будут справедливы следующие выражения:
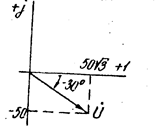
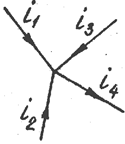
Рис. 3.32 Рис. 3.33
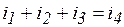 (для мгновенных значении),
(для мгновенных значении),
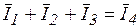 (для векторов действующих значений),
(для векторов действующих значений),
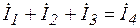 (для комплексов действующих значений).
(для комплексов действующих значений).
 |
Комплексное сопротивление и преобразование схем. Пусть для участка цепи (рис. 3.34) имеем
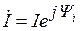 . На комплексной плоскости получим (рис. 3.33).
. На комплексной плоскости получим (рис. 3.33).
Рис. 3.34 Рис. 3.35
Образуем новое комплексное число
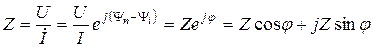
Из 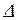 сопротивлений
сопротивлений 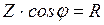 ;
; 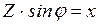
Окончательно полное комплексное сопротивление участка
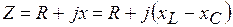 ; здесь
; здесь 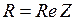 ;
; 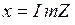 ;
;
полное сопротивление участка 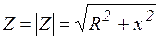 .
.
Пример 3.4. Записать полное комплексное сопротивление цепи на рис. 3.36. В соответствии с последней формулой получим
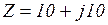
Пример 3.5. Определить для цепи на рис. 3.37.
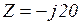 , так как
, так как 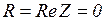 , а
, а 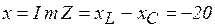
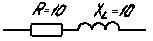 | 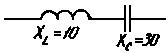 | ||
Рис. 3.36 Рис. 3.37
Использование комплексных сопротивлений облегчает преобразование схем, так как в этом случае справедливы все формулы преобразования цепей постоянного тока.
Пример 3.6. Участок 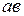 схемы на рис. 3.38 преобразовать в двухэлементный последовательный, если
схемы на рис. 3.38 преобразовать в двухэлементный последовательный, если 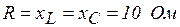 ;
;
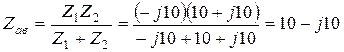 , т. е. В результате преобразования получим схему, представленную на рис. 3.39.
, т. е. В результате преобразования получим схему, представленную на рис. 3.39.
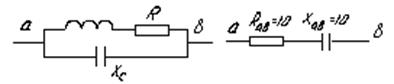 |
Рис. 3.38 Рис. 3.39
Комплексная мощность.
 Пусть
Пусть 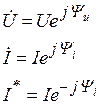
 на комплексной плоскости (рис. 3.40)
на комплексной плоскости (рис. 3.40)
Полная комплексная мощность
Рис. 3.40 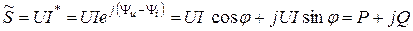 ,
,
т. е. Активная мощность 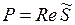 , а реактивная мощность
, а реактивная мощность 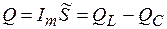 .
.
Пример 3.7. Определить активную, реактивную и полную мощность цепи, если известны 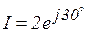 и
и 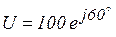 .
.
Решение: 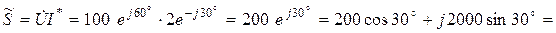
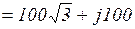 ;
; 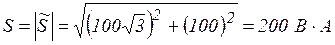
Ответ: 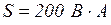 ,
, 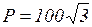 Вт;
Вт; 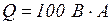 .
.
Понятие о проводимостях. Для участка цепи справедлива векторная диаграмма (рис. 3.41), где 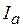 и
и 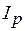 - активная и реактивная составляющие вектора тока;
- активная и реактивная составляющие вектора тока; 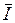 соответственно проекции вектора тока на направление вектора напряжения и на перпендикуляр к нему. Из диаграммы получим
соответственно проекции вектора тока на направление вектора напряжения и на перпендикуляр к нему. Из диаграммы получим 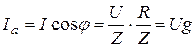 ,
,
где 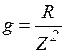 - активная проводимость;
- активная проводимость;
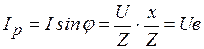 , где
, где
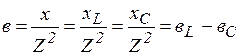 (
( 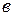 - реактивная,
- реактивная,
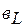 - индуктивная,
- индуктивная, 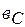 - емкостная проводимости);
- емкостная проводимости);
Рис. 3.41
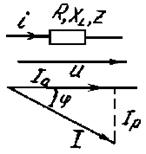
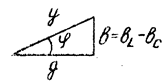
Рис. 3.42
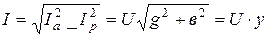
где 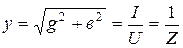 - полная проводимость (обратная полное сопротивлений). Проводимости ветви связаны друг с другом треугольником проводимостей (рис. 3.42).
- полная проводимость (обратная полное сопротивлений). Проводимости ветви связаны друг с другом треугольником проводимостей (рис. 3.42).
Резонансные режимы работы цепей возникают в цепях, содержащих индуктивные катушки и конденсаторы. Признак электрического резонанса - совпадение по фазе тока и напряжения цепи (участка цепи). Такая цепь ведет себя по отношению к источнику подобно резисторному элементу. Различают резонанс в последовательной и в параллельной цепи. Выявим условия, при которых возникают резонансы.
 |
I. Резонанс напряжений возникает при последовательном соединении индуктивных катушек и конденсаторов (рис. 3.45). По II закону Кирхгофа
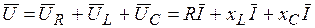 . В соответствии с этим уравнением и с учетом признаке резонанса получим векторную диаграмму (рис. 3.44), из которой следует, что
. В соответствии с этим уравнением и с учетом признаке резонанса получим векторную диаграмму (рис. 3.44), из которой следует, что 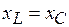 - условие резонанса напряжений или
- условие резонанса напряжений или 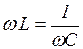 ,
, 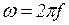 .
.
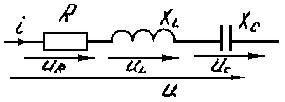 |
Рис. 3.43 Рис. 3.44
Следовательно, резонанс напряжений можно получить путем изменения значений любой из 3 величин: частоты 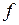 , индуктивности
, индуктивности 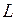 , емкости С. .
, емкости С. .
При резонансе напряжений ток в цепи достигает максимальных значений, так как полное сопротивление становится минимальным:
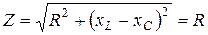 ,
, 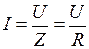 , напряжения на индуктивном и емкостном элементах одинаковы
, напряжения на индуктивном и емкостном элементах одинаковы 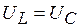 , а
, а 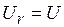 ; реактивная мощность цепи
; реактивная мощность цепи 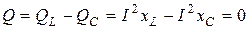 , следовательно, при резонансе активная и полная мощность одинаковы:
, следовательно, при резонансе активная и полная мощность одинаковы: 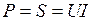 ,
, 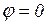
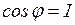 резонансную частоту получим из условия резонанса напряжений
резонансную частоту получим из условия резонанса напряжений 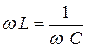 ;
; 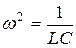 ;
; 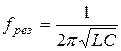
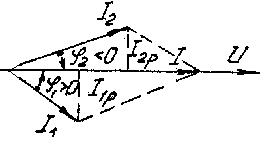
2. Резонанс токов возникает при параллельном соединении индуктивных катушек и конденсаторов (рис. 3.43). Для такой схемы 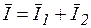 . Строим векторную диаграмму (рис. 3.46): начинаем с вектора напряжений
. Строим векторную диаграмму (рис. 3.46): начинаем с вектора напряжений 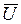 , являющегося общим для обеих ветвей, далее откладываем
, являющегося общим для обеих ветвей, далее откладываем 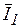 , отстающий от
, отстающий от 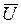 на
на 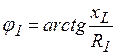 и
и  опережающий
опережающий  на
на  ; далее находим
; далее находим 
Очевидно, что признак резонанса - ток и напряжения должна бить в фазе - будет выполнен, если будут равны составляющие токов 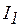 и
и 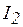 , т. е.
, т. е. 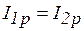 или
или 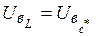 , тогда условием резонанса токов будет равенство реактивных проводимостей:
, тогда условием резонанса токов будет равенство реактивных проводимостей:
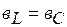 или
или 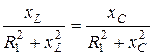 , где
, где 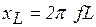 ,
, 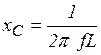 ,
,  ;
;
 |
как видно из формул, резонанс токов можно получить изменением любой из пяди величин:
 ,
,  ,
, 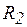 ,
, 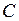 ,
, 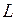 .
.
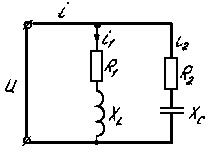 |
Рис. 3.45 Рис. 3.46
При резонансе напряжений 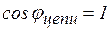 (признак резонанса) реактивная мощность Q = 0 (если умножить уравнение * - на общее напряжение
(признак резонанса) реактивная мощность Q = 0 (если умножить уравнение * - на общее напряжение 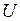 , то
, то 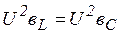 , т. е.
, т. е. 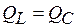 ,
, 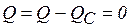 ) и активная мощности цепи численно уравниваются:
) и активная мощности цепи численно уравниваются: 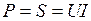 .
.
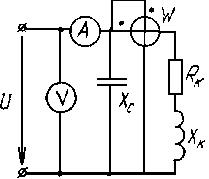 |
Пример 3.8. Определить показания ваттметра, если вольтметр и амперметр соответственно показали 100 В и 2 А. В цепи (рис. 3.47) резонансный режим.
Рис. 3.47
Решение. Ваттметр измеряет активную мощность (по схеме - на катушке); так как в данном случае других потребителей активной мощности, кроме 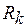 , в схеме нет, то ваттметр измерит активную мощность всей цепи.
, в схеме нет, то ваттметр измерит активную мощность всей цепи.
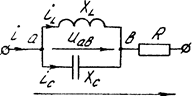
Рис. 3.48
но при резонансе 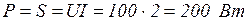
Ответ: показание ваттметра 200 Вт.
Пример 3.9. Определить ток источника 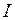 , если
, если 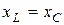 (рис. 3.48).
(рис. 3.48).
Решение. Строим векторную диаграмму (рис. 3.49). Индуктивный и емкостный элементы включены на одно напряжение 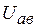 , токи в них по значению одинаковы:
, токи в них по значению одинаковы: 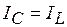 . Построение векторной диаграммы при смешенном соединении элементов удобно начинать с вектора напряжения на параллельном участке (
. Построение векторной диаграммы при смешенном соединении элементов удобно начинать с вектора напряжения на параллельном участке ( 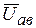 ), далее наносим
), далее наносим 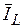 и
и 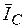 - они в противофазе, следовательно
- они в противофазе, следовательно 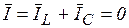 .
.
Ответ: ток источника 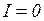
Такая цепь не пропускает ток данной частоты. Если частота изменится, то появится ток ( 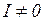 ).
).
Вопросы для самопроверки
1. Какой ток называется переменным?
2. Что такое период, частота, начальная фаза?
3. Как определить начальную фазу синусоидальной величины на временном графике, векторной диаграмме?
4. Каким образом может быть задана синусоидальная величина?
5. Каковы разовые соотношения между током и напряжением на резистивном, индуктивном и емкостном элементах?
6. Привести выражения для индуктивного, емкостного и полного сопротивления. Как изображается  сопротивлений?
сопротивлений?
7. Чем отличается в записи закон Ома и законы Кирхгофа в цепи синусоидального тока от записи для цепи постоянного тока?
8. Привести выражения для реактивной, активной и полной мощностей в цепи синусоидального тока. Как изображается  мощностей?
мощностей?
9. Как записать полное комплексное сопротивление ветви?
10. Как определить полную комплексную мощность цепи, а также активную и реактивную мощности по заданным комплексным напряжению и току цепи?
11. Что является признаком электрического резонанса?
12. Каковы условия резонанса напряжения и токов?
13. Изменением каких параметров можно добиться резонанса напряжений и резонанса токов?
14. Каковы характерные свойства цепей, настроенных в резонансе?
Рис. 4.12 Рис. 4.13
б) Несимметричная нагрузка: 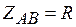 ;
; 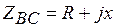 ;
; 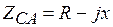 . Фазные токи по-прежнему определяются по формулам (4.1). Линейные токи получим либо из векторной диаграммы на рис. 4.13, либо по формулам.(4.4) и (4.2), где
. Фазные токи по-прежнему определяются по формулам (4.1). Линейные токи получим либо из векторной диаграммы на рис. 4.13, либо по формулам.(4.4) и (4.2), где 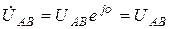 ,
, 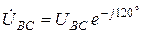 ,
, 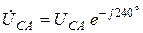 и
и 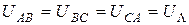 .
.
Мощности в трехфазных цепях. Независимо от способа соединения потребителей (Y или 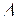 ) при симметричной нагрузке мощность ее равна утроенной мощности одной фазы:
) при симметричной нагрузке мощность ее равна утроенной мощности одной фазы:
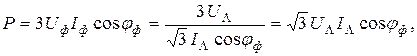 аналогично
аналогично
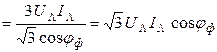 .
.
При несимметричной нагрузке отдельно определяются активная и реактивная мощности каждой фазы» тогда мощность цепи
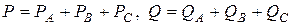 ,
, 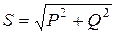
Измерение модности в трехфазной цели.
1. При симметричной нагрузке применяется метод одного ваттметра (рис. 4.14), т.е. измеряется активная мощность одной фазы и результат утраивается: 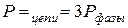
2. Метод двух ваттметров (схема Арона, рис. 4.15) позволяет определить мощность нагрузки (симметричной и несимметричной) при любом способе соединения фаз:
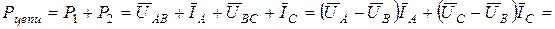
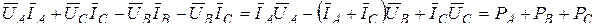 так как
так как 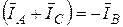
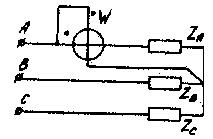 |
Рис. 4.14
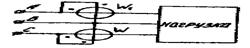 |
5. В четырехпроводной цепи применяется метод трех ваттметров (рис. 4.16):

Рис. 4.15 Рис. 4.16
Вопросы для самопроверки
1. Какие электрические цепи называются трехфазными?
2. Можно ли в трехфазные цепи включать однофазные потребители? Если можно, то как - между линейными проводами или одним из линейных проводов и нейтралью? От чего это зависит?
5. Что такое линейное и фазное напряжения, линейный и фазный токи? Показать на схемах их положительные направления при соединении потребителей звездой, треугольником.
4. Какая нагрузка в трехфазной цепи называется симметричной?
5. Каково соотношение между фазными и линейными напряжениями симметричного потребителя при соединении звездой?
6. Каково соотношение между фазными и линейными токами симметричного потребителя при соединении треугольником?
7. чем объяснить наличие четвертого (нейтрального) провода в трехфазных цепях?
8. Почему в нейтраль не включают предохранители?
9. Как определить ток в нейтрали?
10. Как определить полную мощность трехфазной цепи при заданном количестве потребителей, однофазных и трехфазных?
11. Сколько ваттметров и как нужно включить для измерения активной мощности симметричного трехфазного потребителя?
12. В чем сущность метода двух ваттметров? Можно ли использовать этот метод в четырехпроводных цепях?
15. Сколько ваттметров и как нужно включить, чтобы измерить активную мощность несимметричной нагрузки в четырехпроводной цепи?
14. Каков порядок построения векторной диаграммы при соединении симметричного потребителя звездой, треугольником?
Эквивалентная синусоида.
Если несинусоидальное напряжение и ток не слишком заметно отличаются от синусоид, то при приближенных расчетах несинусоидальные напряжения и токи заменяют эквивалентными синусоидальными, имеющими такие же действующие значения.
Синусоиду, заменяющую несинусоидальную кривую, называют эквивалентной.
Эквивалентный синусоидальный ток должен быть сдвинут по фазе относительно напряжения на такой угол 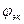 , чтобы активная мощность при эквивалентном синусоидальном токе равнялась активной мощности при несинусоидальном токе:
, чтобы активная мощность при эквивалентном синусоидальном токе равнялась активной мощности при несинусоидальном токе:
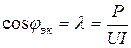
2.3. Режим в цепи при приложенном к ней несинусоидальном напряжении.
Если напряжение на выводах линейной цепи не синусоидально, то его можно представить в виде ряда Фурье:
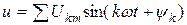
При этом напряжении ток в цепи:
R 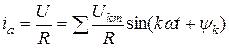
L 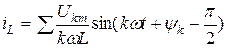
C 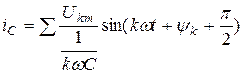
То есть каждой гармонике напряжения соответствует своя гармоника тока. Расчет ведется для каждой гармоники напряжения отдельно любым методом (комплексным, векторным).
Результирующие токи и напряжения определяются как алгебраическая сумма мгновенных значений токов и напряжений отдельных гармоник.
Реактивное сопротивление определяется отдельно для каждой гармоники.
При несинусоидальном напряжении на выводах линейной цепи, содержащей L, C, в цепи могут возникать резонансные явления, как на основной, так и на высших гармониках.
Пример: Напряжение на зажимах цепи
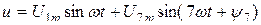
Цепь состоит из последовательного соединения R и L. Следовательно:
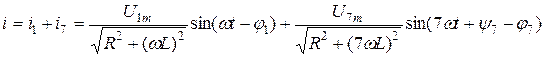
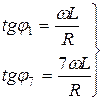 – определяем сдвиги фаз.
– определяем сдвиги фаз.
Электрические фильтры
Электрические фильтры – четырехполюсники, содержащие реактивные элементы, которые либо задерживают, либо пропускают к приемнику токи одного или нескольких заданных диапазонов частот. Электрические фильтры широко применяются в радиотехнике, связи, электроэнергетике и т. д.
В основе принципа действия фильтра лежит зависимость его эквивалентного сопротивления Z э от частоты. Комбинируя схемы соединения индуктивности и емкости, можно получить фильтры следующих типов:
Низкочастотные – пропускают токи в диапазоне частот 0 – ω0.

Zэ 
L L
С
ω0 ω
Т-образная схема. Широко применяются в качестве сглаживающих выпрямительных устройств.
Высокочастотные.

 Zэ
Zэ
C C
L
ω
Полосовые пропускают токи в заданном диапазоне частот ω1 – ω2.

L1 C1 Zэ
L2 C2
ω1 ω2 ω
Заградительные имеют полосу пропускания тока от 0 до ω1 и от ω2 до ∞.
C C Zэ
 | |||
 | |||
L L L
C
ω1 ω2 ω
В маломощных электрических цепях (в радиоэлектронике, связи) полосовые и заградительные фильтры часто выполняют на основе резисторов и конденсаторов.
Низкочастотный RC-фильтр используется для сглаживания пульсаций тока в маломощных выпрямительных схемах.

 Zэ
Zэ
R C
ω
Включение активного сопротивления необходимо для ограничения тока при подключении схемы к источнику питания. При отсутствии R в момент включения Xc очень мало и источник оказывается в режиме короткого замыкания. Введение R хотя и увеличивает потери мощности, но обеспечивает защиту источника от короткого замыкания.
Сглаживающие фильтры.
Для питания ряда узлов электронной аппаратуры обычно требуется постоянное напряжение. Напряжение на выходе выпрямительных схем является или пульсирующим (трехфазный выпрямитель), или импульсным (одно- и двухполупериодный выпрямитель). Для того, чтобы выпрямленное напряжение имело требуемую форму, применяют сглаживающие фильтры.
Количественно работа фильтра характеризуется коэффициентом сглаживания пульсаций q, который показывает, во сколько раз уменьшается пульсация при прохождении сигнала через данный фильтр:
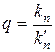 , где
, где  – коэффициент пульсаций до прохождения фильтра,
– коэффициент пульсаций до прохождения фильтра,
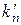 – коэффициент пульсаций после прохождения фильтра.
– коэффициент пульсаций после прохождения фильтра.
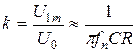
Кроме того, в фильтре не должно быть значительных потерь постоянной составляющей выпрямленного напряжения.
Сглаживающие фильтры подразделяются на емкостные, индуктивные, индуктивно-емкостные и резисторно-емкостные.
Наиболее простой емкостной фильтр. Работа основана на способности конденсатора быстро запасать электроэнергию, а затем относительно медленно отдавать ее в нагрузку.
 Д
Д
Uд
U Cф Rн
Uн=Uc
Когда U д = u - Uc >0, диод открыт и Сф заряжается (t1÷t2). Так как сопротивление Д мало, то Сф успевает зарядиться почти до u .
 u
u
Uн, Uн
ic ic
t1 t2 t
Когда U - Uc<0, диод закрыт и Cф медленно разряжается через Rн до тех пор, пока напряжение источника u снова не станет больше Uc. Время зарядки зависит от постоянной времени τ= C ф R н, которая показывает, в течение какого времени напряжение на Cф уменьшится в 2,72 раза.
Емкостные фильтры используются в выпрямителях малой мощности.
В выпрямителях с большими токами применяют индуктивные фильтры (дроссель с относительно большой индуктивностью).
 a
a
Др Rн
U1 U2 b

uab,
iн uab iн
t
За счет явления самоиндукции ток i н не падает до нуля при нулевом напряжении Uab и коэффициент пульсации заметно меньше (в однополупериодном выпрямителе применение нецелесообразно).
На практике применяют комбинированные фильтры:
Lф Lф
 |  |
Cф Rн Cф Cф Rн
Г-образный П-образный
Эти фильтры обеспечивают хорошее сглаживание тока в нагрузке. Напряжение на входе фильтра – сумма постоянной составляющей и целого ряда гармоник. На индуктивном сопротивлении выделяется большая часть переменной, а на емкостном – большая часть постоянной составляющей напряжения выпрямителя.
В маломощных схемах дроссель может быть заменен резистором. Уменьшается масса, габариты и стоимость, однако сглаживание ухудшается.
Пример. Конденсатор хорошо сглаживает пульсации, если выполняется условие
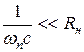 ,
,
ωн – частота пульсаций. Кроме того, R н >> R д.
τзар=RвнС, Rвн=Rд+R2, т.к. Rн>>Rд, то τраз>>τзар. τраз=RC
 f = 50 Гц
f = 50 Гц
Rд Em Д Rн = 4 кОм
Rн Rвн = 200 Ом
C = 40 мкФ
C
В этом случае период пульсаций
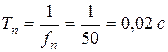
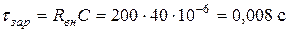
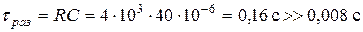
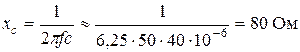
xc << R н
80 Ом << 4 кОм
Таблица 5.1
| 1 | 2 | 3 | 4 |
|
|
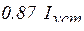
|
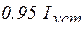
|
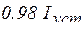
|
(рис. 5.5)
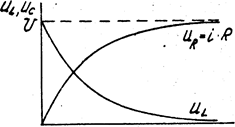
Напряжение на индуктивном элементе в переходный период (рис. 5.3)
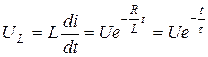 (5.9)
(5.9)
Характер изменения величин в цепях с одним накопителем энергии подчиняется экспоненциальному закону. Таким образом, задача сводится к определению конкретных значений начальных и остановившихся токов и напряжений.
Пример 5.1. По какому закону будут изменяться токи 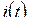 ,
, 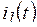 ,
, 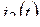 и напряжение
и напряжение 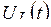 цепи на рис. 5.4 при переходном процессе, вызванном замыканием рубильника?
цепи на рис. 5.4 при переходном процессе, вызванном замыканием рубильника?
Решение сводится к определению начальных и установившихся значений токов и напряжений. Так как ток в катушке индуктивности скачком изменяться не может (см. формулу (5.2)), схема для определения начальных значений величин примет вид, изображенный на рис. 5.5, где
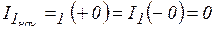
Остальные токи, напряжения в схеме определяются как обычно для цепей постоянного тока: 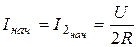 ;
; 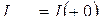 ;
; 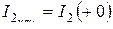 ;
;
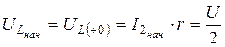
 Схема на рис. 5.6 для установившегося режима получена при
Схема на рис. 5.6 для установившегося режима получена при  , а
, а 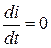 и
и 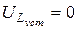


Рис.5.4 Рис. 5.5 Рис. 5.6
Кривые изменения токов и напряжений изображены на рис. 5.7 и рис. 5.8.
Отключение цепи с 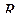 и
и 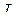 от источника постоянного напряжения. При отключении индуктивной катушки от источника (рис.5.9) ток в ней
от источника постоянного напряжения. При отключении индуктивной катушки от источника (рис.5.9) ток в ней 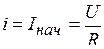 в первый момент времени остается неизменным, зато в резисторе
в первый момент времени остается неизменным, зато в резисторе 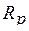 ток
ток 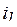 меняется скачком от нудя до -
меняется скачком от нудя до -  (знак минус показывает, что он направлен против указанного на схеме положительного направления). Для уменьшения потерь в цепи при включенной катушке последовательно с разрядным сопротивление включен диод Д, благодаря чему ток
(знак минус показывает, что он направлен против указанного на схеме положительного направления). Для уменьшения потерь в цепи при включенной катушке последовательно с разрядным сопротивление включен диод Д, благодаря чему ток 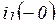 до размыкания выключателя равен нулю.
до размыкания выключателя равен нулю.
Согласно второму закону Кирхгофа, 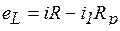 ; так как
; так как 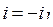 , то
, то
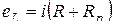 или
или 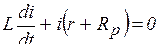
Отсутствие правой части в уравнении означает, что ток в переходном процессе равен свободной составляющей (энергия извне не поступает) 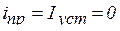
Ток в цепи 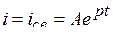
Поскольку 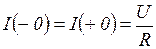 , то
, то 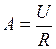 .
.
Таким образом, 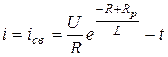 ток в разрядном сопротивлении
ток в разрядном сопротивлении 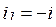 (рис. 5.10).
(рис. 5.10).
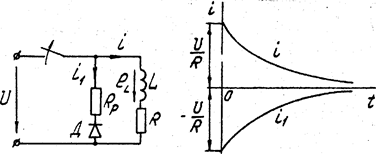
Рис. 5.9 Рис. 5.10
Включение цепи с  и
и  на постоянное напряжение. Для цепи (рис. 5.11) по второму закону Кирхгофа
на постоянное напряжение. Для цепи (рис. 5.11) по второму закону Кирхгофа 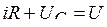 ; так как
; так как 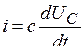 , получаем уравнение
, получаем уравнение
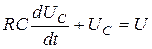
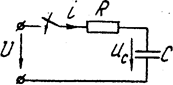
Рис. 5.11
Напряжение на конденсаторе в процессе заряда (рис. 5.12)
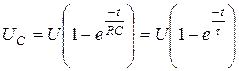 (5.14)
(5.14)
Ток в цепи заряда конденсатора
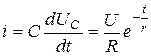 (5.15)
(5.15)
где 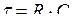 .
.
Пример 5.2. Определить начальные и установившиеся значения токов  ,
, 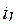 ,
, 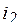 , и напряжений
, и напряжений 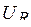 ,
, 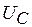 в цепи, изображенной на рис. 5.13, при замыкании ключа.
в цепи, изображенной на рис. 5.13, при замыкании ключа.
Решение. Схема для определения начальных стечении величин при  изображена на рис. 5.14, где
изображена на рис. 5.14, где 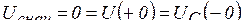 ,
,
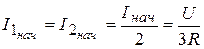
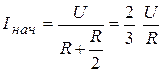 ,
, 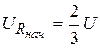
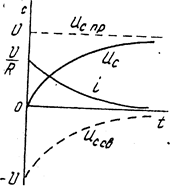
Рис. 5.12
Схема для определения установившихся значений величин при  приведена не рис. 5.15.
приведена не рис. 5.15.
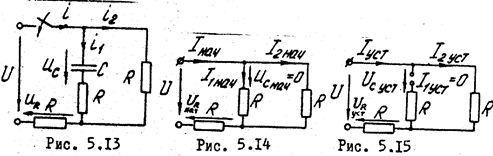
Известно, что постоянный ток через емкость в установившемся процессе не проходит: 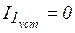 ,
, 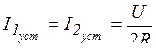 ,
, 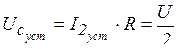 ,
, 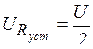
Разряд конденсатора на сопротивление 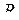 . Уравнение для цепи (рис. 5.16), составленное по второму закону Кирхгофа, имеет вид
. Уравнение для цепи (рис. 5.16), составленное по второму закону Кирхгофа, имеет вид 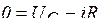 , где
, где 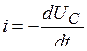 - знак минус означает, что направление тока при разряде конденсатора не совпадает с положительным направлением напряжения
- знак минус означает, что направление тока при разряде конденсатора не совпадает с положительным направлением напряжения 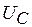 . В конце процесса
. В конце процесса 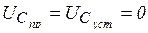 . Поэтому
. Поэтому 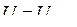 ,
, 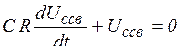
Решение этого уравнения имеет вид
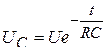
а ток разряда
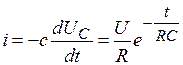
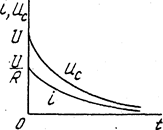
Рис. 5.17
Графики изображены на рис. 5.17.
Вопросы для самопроверки
1. Почему ток в цепи с индуктивной катушкой не может измениться скачком?
2. Могут ли напряжения на конденсаторе и ток через конденсатор меняться скачком?
3. Что такое постоянная времени электрической цепи?
4. 0т чего зависит быстрота окончания Рис. 5.17 переходного процесса (в цепи с  и
и  , в цепи с
, в цепи с  и
и 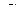 )?
)?
5. В каких цепях при коммутации переходный процесс отсутствует?
6. Назовите причины возникновения переходных процессов в электрических цепях.
7. Как определить постоянную времени по графику?.
Линейные электрические цепи постоянного тока.
Задачи анализа и расчета электрических цепей. Положительные направления напряжения, ЭДС и тока. Источниками электрической энергии являются устройства, в которых различные виды энергии превращаются в электрическую. Важнейшей характеристикой источника служит электродвижущая сила (ЭДС). ЭДС является причиной возникновения напряжения U и тока I в электрической цепи. Одной из задач анализа и расчета электрической цепи является определение токов, напряжений и мощностей на различных ее участках. Для этого необходимо знать ЭДС и сопротивления источников и приемников. В некоторых случаях ЭДС с внутренним сопротивлением может отсутствовать в электрической цепи в явном виде. Вместо этого указывается напряжение, подводимое к электрической цепи от источника, а последний только подразумевается.
При расчете цепи кроме известных направлений величин задаются еще произвольные направления для искомых величин, которые считают положительными
( Е>0, U >0 и I>0).
Электрическая цепь. Основные понятия. Электрическая цепь -это совокупность источников, потребителей и связывающих их устройств. Простейшая цепь представлена на рис. 1.1.
При описании сложной электрической цепи (рис. 1.2) используются понятия: узел, ветвь, контур.
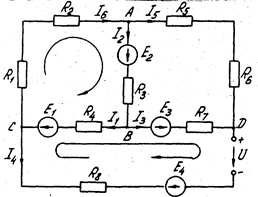
Рис 1.1 Рис 1.2
Узел - это точка, в которой сходятся не менее трех ветвей (точки А, В, С, D).
Ветвь - это часть цепи, где все элементы соединены последовательно, а токи в них всегда одинаковы (ветви АС, СВ. АВ и т.д.). Контур - это замкнутая в геометрическом смысле часть цепи (контур АВСА).
Основные законы электрических цепей. Согласно закону Ома, ток в замкнутой неразветвленной цепи (см. рис. 1.1)
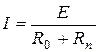 (1.1)
(1.1)
Для участка цепи, не содержащего источника ЭДС, закон Ома имеет вид
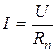 (1.2)
(1.2)
(рис. 1.1, правая часть цепи).
Согласно первому закону Кирхгофа, сумма токов, направленных к узлу А (рис. 1.3), равна сумме токов, направленных от узла. Если токи, направленные к узлу, считать положительными, а направленные от узла - отрицательными, то, обобщая, можно сказать:
алгебраическая сумма токов, сходящихся в узле, равна нулю, т.е.
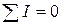 (1.3)
(1.3)
для точки А 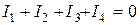 .
.
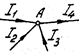 Согласно второму закону Кирхгофа, во всяком замкнутом в геометрическом смысле контуре алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на всех сопротивлениях контура и напряжений:
Согласно второму закону Кирхгофа, во всяком замкнутом в геометрическом смысле контуре алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на всех сопротивлениях контура и напряжений:
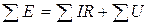 (1.4) Рис 1.3
(1.4) Рис 1.3
Чтобы записать второй закон Кирхгофа для конкретного контура, нужно:
1) обозначить положительные направления ЭДС, токов и напряжений; .
2) выбрать направление обхода контура;
5) составить уравнение по второму закону Кирхгофа. Со знаком плюс в соответствующую часть уравнения входят те ЭДС, токи и напряжения, положительные направления которых совпадают с направлением обхода. Так, на рис. 1.2 для контура АВСА
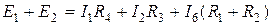
для контура СВДС
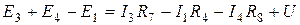
Электрическая энергия и мощность. Мощность - это интенсивность энергетического процесса 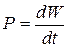 . Для постоянного тока
. Для постоянного тока 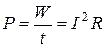 .
.
Для источника (рис. 1.1)
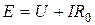
После умножения на ток I получим уравнение баланса мощности цепи 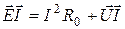 . Баланс мощности - это отражение закона сохранения энергии для электрической цепи;
. Баланс мощности - это отражение закона сохранения энергии для электрической цепи; 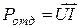 - мощность, отдаваемая источником во внешнюю цепь. Напряжение и ток совпадают по направлению. Мощность, вырабатываемая источником,
- мощность, отдаваемая источником во внешнюю цепь. Напряжение и ток совпадают по направлению. Мощность, вырабатываемая источником, 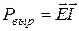 . Ток совпадает по направлению с УДС.
. Ток совпадает по направлению с УДС.
Мощность, расходуемая на нагрев внутреннего сопротивления источника, 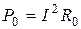 .
.
Коэффициент полезного действия:
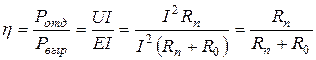
При передаче потребителям одной и той же мощности 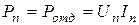 ток в проводах будет тем меньше, чем больше напряжение
ток в проводах будет тем меньше, чем больше напряжение 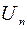 установки. При этом уменьшаются потери мощности в проводах:
установки. При этом уменьшаются потери мощности в проводах:
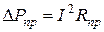 , когда
, когда 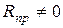 .
.
Режимы работы источника электрической энергии. Характерными являются режимы: номинальный, холостого хода, короткого замыкания.
Номинальный режим работы - это режим, для которого рассчитан источник. Он характеризуется номинальным напряжением, током, мощностью. Номинальные напряжения стандартизированы: 110, 220, 440 В. Номинальные токи 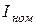 , лимитируются предельно допустимыми температурами нагрева этих устройств.
, лимитируются предельно допустимыми температурами нагрева этих устройств.
Номинальная мощность  . для электрического источника - это полезная мощность, отдаваемая им во внешнюю цепь при номинальных условиях работы,
. для электрического источника - это полезная мощность, отдаваемая им во внешнюю цепь при номинальных условиях работы,
Режимы холостого хода и короткого замыкания являются предельными режимами работы источника:
а) режим холостого хода - внешняя цепь разомкнута;
б) режим короткого замыкания - зажимы источника замкнуты проводником, сопротивление которого ничтожно мало.
 Используя уравнение источника
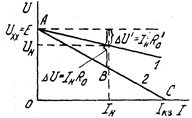
Используя уравнение источника 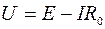 , можно начертить его внешнюю характеристику
, можно начертить его внешнюю характеристику 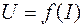 (рис. 1.4). При
(рис. 1.4). При 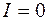
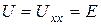 (точка А), при
(точка А), при 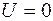
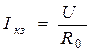 (точка С).
(точка С).
Рис 1.4
Ток короткого замыкания 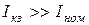 и представляет опасность для источника. На рис. 1.4 видно, что чем больше внутреннее сопротивление источника, тем больше влияние тока на напряжение потребителя.
и представляет опасность для источника. На рис. 1.4 видно, что чем больше внутреннее сопротивление источника, тем больше влияние тока на напряжение потребителя.
Электрические цепи с одним источником. Анализ и расчет цепей с одним источником проводится с использованием законов Ома и Кирхгофа, а в более сложных случаях еще и методом эквивалентных преобразований.
Для последовательного соединения сопротивлений (рис. 1.5)
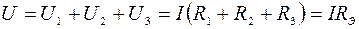 , откуда
, откуда
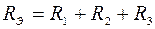
Для параллельного соединения сопротивлений (рис. 1.6)
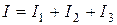 или
или 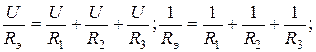
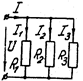
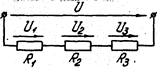
Рис 1.5 Рис 1.6
В частном случае для двух соединений 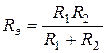 .
.
Эквивалентная проводимость 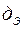 для парралельного участка
для парралельного участка 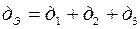 .
.
Отдельно можно выделить смешанное соединение (рис. 1.7).
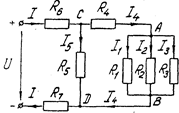
Рис 1.7
Это такое соединение, при котором на одних участках электрической цепи сопротивления соединены последовательно, а на других параллельно.
Пример. В цепи, изображенной на рис. 1.7,  ,
, 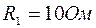 ,
, 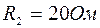 ,
, 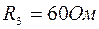 ,
,
Найти распределение токов в схеме.
Решение. Эквивалентное сопротивление между точками А и В
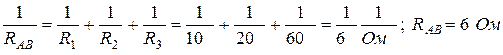
Сопротивление 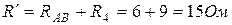
Сопротивление 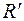 параллельно сопротивлению
параллельно сопротивлению 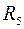
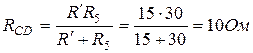
Общее сопротивление цепи
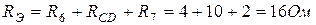
Общий ток
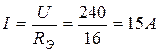
Напряжение между точками С и D
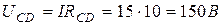
Токи в сопротивлениях 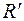 и
и 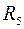 определяются по закону Ома
определяются по закону Ома
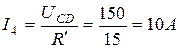 ,
, 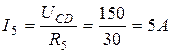
Напряжение между точками А и В

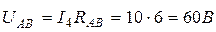
Токи в сопротивлениях 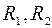 и
и 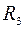
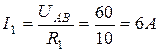 ;
; 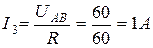 ;
; 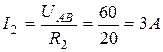
Электрические цепи с несколькими источниками, методом анализа и расчета сложных цепей является непосредственное применение первого и второго законов Кирхгофа.
Расчет сложной цепи (рис. 1.8) проводят в такой последовательности:
1) упрощают схему;
2) по первому закону Кирхгофа составляют ( 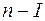 ) уравнений, где
) уравнений, где 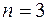 - число узлов в схеме;
- число узлов в схеме;
3) по второму закону Кирхгофа составляют не достающие уравнения т -( п -I), где
т = 5 - число ветвей схемы.
Если в результате решения токи получатся отрицательными, это значит, что действительные направления токов противоположны выбранным.
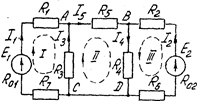 Пример. Определить токи в цепи на рис. 1.8, применив законы Кирхгофа, если
Пример. Определить токи в цепи на рис. 1.8, применив законы Кирхгофа, если 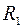 = 0,3 Ом, R2=R6=0,4 Oм, R3=R4=2 Oм, R5 =6 Oм, R7=0,6 Oм, E1=140В, Е2=85В, R01=0,1Ом, R02=0,2Ом
= 0,3 Ом, R2=R6=0,4 Oм, R3=R4=2 Oм, R5 =6 Oм, R7=0,6 Oм, E1=140В, Е2=85В, R01=0,1Ом, R02=0,2Ом
Рис 1.8
Решение. На основании первого закона Кирхгофа записываем два уравнения, т.е. (n-1), где n=3:
для узла А 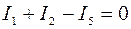
для узла В 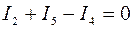
Направления обхода контуров выбираем произвольно. Число ветвей т = 5. Столько же неизвестных токов, поэтому уравнений согласно второму закону Кирхгофа три:
для контура I 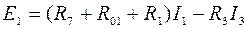 ;
;
для контура II 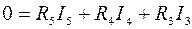 ;
;
для контура III 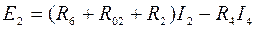
Во втором контуре нет ЭДС, и левая часть уравнения равна 0.
Решение системы с пятью неизвестными дает: 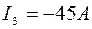 (знак минус означает, что действительное направление тока противоположно принятому на схеме),
(знак минус означает, что действительное направление тока противоположно принятому на схеме), 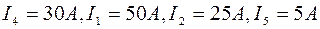
На участке DC ток 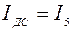 и направлен от точки D и С.
и направлен от точки D и С.
Дата: 2018-12-21, просмотров: 733.