Нелинейный элементы - это разнообразные электронные, полупроводниковые приборы и устройства, электрическая дуга и др.

Определяющей функцией нелинейных элементов является вольтамперная характеристика (ВАХ), представляющая собой зависимость между током нелинейного элемента и напряжением на его зажимах:

U ( I ) или I ( U ) (рис. 1.9 б, в).

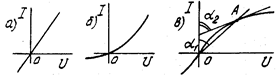
рис 1.9

Для линейных элементов 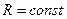, зависимость I (U) линейная и ВАХ представляется прямой линией, проходящей через начало координат (рис. 1.9а).

Имея ВАХ нелинейного элемента, можно определить его сопротивление при различных токах (напряжениях).

Различают два вида сопротивлений нелинейных элементов: статическое и дифференциальное. Статическое сопротивление характеризуется тангенсом угла наклона секущей к оси ординат:

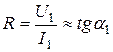
Дифференциальное сопротивление пропорционально тангенсу угла наклона касательной, проведенной к ВАХ в данной точке, к оси ординат:

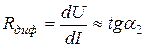
При расчете нелинейных цепей обычно пользуются графоаналитическими методами, основанными на применении законов Кирхгофа и заданных ВАХ.

При этом электрическую цепь заменяют эквивалентной цепью, имеющей эквивалентную ВАХ.

Последовательное соединение, нелинейных элементов. Общее напряжение U всегда равно сумме напряжений U=U₁+U₂ (рис. 1.10 a).

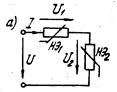
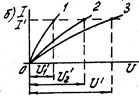
Рис 1.10

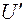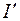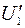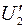Если известно напряжение U , то ток I можно определить, построив результирующую ВАХ цепи (кривая 3 на рис. 1.10 б). Для построения следует суммировать абсциссы кривых 1 и 2, соответствующие одним и тем же значениям тока. Пользуясь полученным графиком, можно для любого значения напряжения  найти ток  (рис. 1.10 б). Этот ток определит напряжения  и  на каждом из нелинейных сопротивлений.

Если цепь состоит только из двух сопротивлени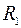й  и 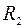 и требуется найти лишь одно значение тока при заданном напряжении U ' , то используют метод опрокинутой характеристики, т.е. взамен одной из вольтамперных характеристик (например, кривой 1) строят ее зеркальное отображение- кривую 3 (рис. 1.11). Начало координат кривой должно быть перенесено в точку 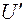. Точка пересечения характеристик 2 и 3 определяет ток I в цепи, а также напряжения  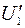и 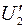 на сопротивлениях вели. Так проводят графическое решение уравнения .

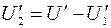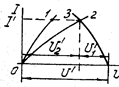
Рис 1.11

Пример. Определить ток в схеме       

(рис. 1.12 а), если Е = 100 В, 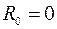, 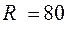Ом. ВАХ нелинейного элемента изображена на рис.1.12 б.

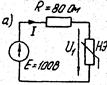
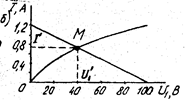
Рис 1.12 а                       Рис 1.12 б

Решение. Составляем уравнение

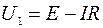
Графическое его решение - точка пересечения двух функций. Нелинейная часть уравнения построена в виде функции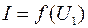

Линейная часть представляет собой ВАX источника с внутренним сопротивлением 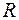. Ее строим по двум точкам - точкам холостого хода и короткого замыкания источника:

1)

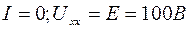
2)

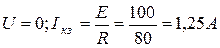
Соединяем полученные точки отрезком пряной. Координаты точки пересечения М дают соответственно ток 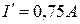 и на­пряжения  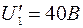на нелинейном элементе.

При параллельном соединении, двух сопротивлений (рис. 1.13 а) ток в неразветвленной части цепи равен сумме токов в отдельных ветвях:

.

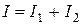Поэтому при построении результирующей ВАХ всей цепи следует суммировать ординаты графиков 1 и 2 (рис. 1.13 б), соответствующие одним и тем же значениям напряжения.

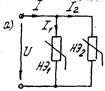
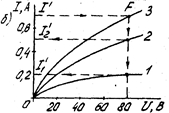
 Рис 1.13 а             Рис 1.13 б

Пример. Какие токи проходят в параллельных ветвях, содержащих нелинейные элементы 1 и 2 (рис. 1.13 а), если ток 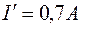. ВАХ нелинейных элементов показаны на рис. 1.13 б.

Решение: Для данной схемы .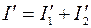

Строим эквивалентную ВАХ. По ней, зная ток 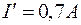 находим входное напряжение 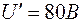(точка 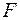). При этом напряжении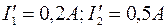

В случае смешанного соединения расчет производят заменой сначала параллельного участка, а затем полученного последовательного.

Вопросы для самопроверки

1. Как определить ток в простой неразветвленной цепи с одним источником?

2. Как определить ток на участке цепи?

3. Чему равен ток в последовательной цепи, если известен ток в ее отдельных элементах?

4. Чему равен ток в неразветвленной электрической цепи, если известны токи в каждом сопротивлении, включенном параллельно?

5. Чему равно напряжение на выходных зажимах источника, если известны его параметры и ток нагрузки?

6. На сколько напряжение на зажимах источника отличается от его ЭДС?

7. Что такое мощность электрической цепи?