Электрические цепи переменного тока имеют ряд особенностей по сравнению с цепями постоянного тока: переменные токи и напряжения отдельных элементов создают в них переменные магнитные и электрические поля, в результате чего в цепи возникают явления само- и взаимоиндукции, оказывающие существенное влияние на процессы в цепях.
Переменный ток - ток, изменяющийся во времени.
Мгновенное значение тока 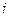 - значение тока в данный момент.
- значение тока в данный момент.
Периодические токи - токи, значения которых повторяются через равные промежутки времени в той же последовательности.
Период 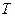 - наименьший промежуток времени, через который
- наименьший промежуток времени, через который
эти повторения наблюдаются.
Частота 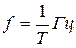
Наибольшее распространение в электротехнике получили токи, являющиеся синусоидальными функциями времени.
Принцип возбуждения ЭДС рассмотрим на простейшем примере.
Приведем во вращение с постоянной угловой скоростью 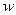 магнит
магнит 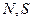 (рис. 3.1), тогда в проводнике
(рис. 3.1), тогда в проводнике 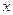 , условно представляющем обмотку генератора, расположенную на неподвижном статоре, возбудится ЭДС
, условно представляющем обмотку генератора, расположенную на неподвижном статоре, возбудится ЭДС 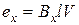 . С учетом того, что в произвольной точке
. С учетом того, что в произвольной точке 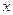 индукция
индукция 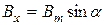 , имеем
, имеем 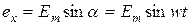 , где
, где 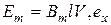 - мгновенное значение;
- мгновенное значение; 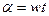 - фазовый угол, или фаза, определяющая значение функции в данный момент времени.
- фазовый угол, или фаза, определяющая значение функции в данный момент времени.
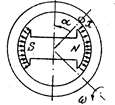
Рис 3.1
Очевидно, что поворот магнита на  будет соответствовать периоду
будет соответствовать периоду  , тогда
, тогда
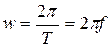 .
.
На рис. 3.2 показано построение графика 
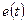 - временной диаграммы
- временной диаграммы
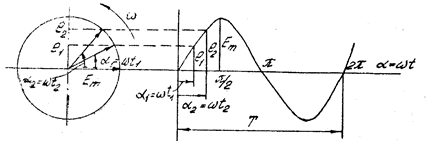
Рис 3.2
вращением вектора 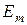 с
с 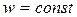 , здесь
, здесь 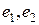 -мгновенные значения ЭДС в моменты времени соответственной
-мгновенные значения ЭДС в моменты времени соответственной 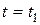 и
и 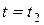 ;
; 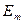 амплитудное (максимальное) значение ЭДС. Из рис. 3.2 следует:
амплитудное (максимальное) значение ЭДС. Из рис. 3.2 следует:
1) мгновеннное значение - проекция вектора амплитудного значения синусоидальной величины на ось ординат;
2) синусоидальная величина может быть представлена: а) тригонометрической функцией, б) временной диаграммой (рис. 3.3) и в) вращающимся вектором (рис. 3.4).
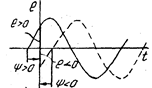
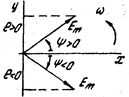
рис 3.3 рис 3.4
Если при 
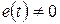 - есть начальная фаза ЭДС (значение аргумента, определяющее функцию при
- есть начальная фаза ЭДС (значение аргумента, определяющее функцию при 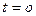 ), то
), то 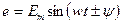 , где
, где 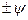 -фазовый угол (начальная фаза ).
-фазовый угол (начальная фаза ).
Из рассмотрения пп. а)-в) следует правило отсчета начальных фаз:
Начальная фаза на временной диаграмме отсчитывается от нуля синусоиды к началу отсчета, при этом 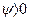 , если отсчет идет в сторону увеличения чисел по числовой оси,
, если отсчет идет в сторону увеличения чисел по числовой оси, 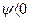 , если наоборот.
, если наоборот.
Если начальные фазы разные, существует сдвиг по фазе, если разность начальных фаз 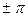 - функции в противофазе (рис. 3.5).
- функции в противофазе (рис. 3.5).
Пример 3.1. Известен закон изменения напряжения 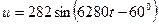 и тока
и тока 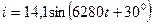 .
.
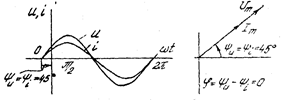
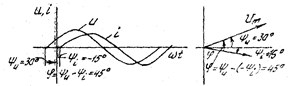
Рис 3.5
Определить период 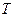 , представить данные величины временными графиками и вращающимися векторами, и определить фазовый сдвиг между током и напряжением.
, представить данные величины временными графиками и вращающимися векторами, и определить фазовый сдвиг между током и напряжением.
Решение: угловая частота 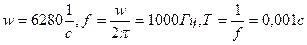 . Временные графики и векторная диаграмма даны на рис. 3.6, 3.7. Ток опережает напряжение на 30° по фазе.
. Временные графики и векторная диаграмма даны на рис. 3.6, 3.7. Ток опережает напряжение на 30° по фазе.

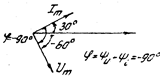
Рис 3.6 Рис 3.7
Действующее значение синусоидального тока, напряжения, ЭДС. Действующим значением переменного тока 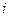 называется такой постоянный ток
называется такой постоянный ток 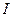 , который в резисторе
, который в резисторе 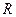 (рис. 3.8) за время
(рис. 3.8) за время 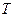 выделяет ту же тепловую энергию, что и данный переменный ток
выделяет ту же тепловую энергию, что и данный переменный ток 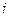 за то же время.
за то же время.
 Уравнение для тепловых энергий i R
Уравнение для тепловых энергий i R



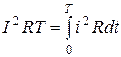 , откуда
, откуда 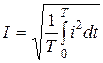 - действующее
- действующее 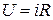
значение переменного тока. Рис. 3.8
В частном случае для синусоидального тока получим 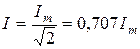 , аналогично
, аналогично 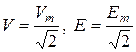 . Большинство измерительных приборов (электромагнитной, электродинамической и других систем) фиксируют именно действующее значение.
. Большинство измерительных приборов (электромагнитной, электродинамической и других систем) фиксируют именно действующее значение.
Сложение синусоидальных величин. Векторная диаграмма.
Определить 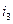 (рис. 3.9), если
(рис. 3.9), если 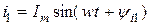 и
и 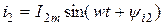 . Пусть
. Пусть 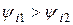 . В соответствии с I законом Кирхгофа
. В соответствии с I законом Кирхгофа 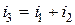 (для мгновенных значений). Проще всего выполнить такое сложение, если данные токи представить вращающимися векторами (рис. 3.10).
(для мгновенных значений). Проще всего выполнить такое сложение, если данные токи представить вращающимися векторами (рис. 3.10).
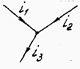

Рис 3.9 Рис 3.10
Легко убедиться, что проекция вектора, полученного в результате геометрического сложения векторов 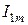 и
и 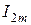 на ось ординат, представляет собой мгновенное значение тока
на ось ординат, представляет собой мгновенное значение тока 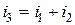 .
.
Таким образом, уравнению 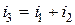 соответствует уравнение для векторов амплитудных значений
соответствует уравнение для векторов амплитудных значений 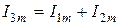 последнее уравнение разделить на
последнее уравнение разделить на 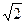 , то получим аналогичное уравнение для векторов, действующих значений:
, то получим аналогичное уравнение для векторов, действующих значений: 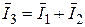
Вывод 1. Каждому линейному соотношению между мгновенными значениями синусоидальных величин одинаковых частот соответствует точно такое же соотношение между векторами амплитудных и действующих значений. Мгновенные значения складываются алгебраически, а показания приборов (действующие значения) - геометрически.
Совокупность нескольких векторов, изображающих синусоидальные величины одинаковой частоты - векторная диаграмма.
Элементы цепей переменного тока. Основные соотношения.
Для анализа и расчета электрических цепей используют схемы замещения, составленные из идеализированных элементов, каждый из которых учитывает только одно физическое явление или процесс в реальной электрической цепи. Таких элементов три: резистивный, индуктивный и емкостный. Они учитывают соответственно необратимое преобразование электрической энергии в тепловую, возникновение переменных магнитных и электрических полей. Параметрами этих элементов являются активное сопротивление 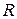 , индуктивность
, индуктивность 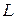 и емкость
и емкость 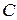 .
.
Основные соотношения для идеализированных элементов.
1) Резистивный элемент. Параметр - активное сопротивление 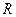 (рис. 3.11). Пусть
(рис. 3.11). Пусть 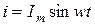 , тогда
, тогда 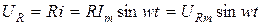 ; здесь
; здесь 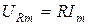 или, разделив уравнение на
или, разделив уравнение на 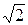 получим
получим 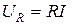 .
.
Вывод 1: Сравнивая начальные фазы 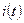 и
и 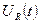 , видим, что ток и напряжение на резистивном элементе совпадают по фазе. (рис 3.12, 3.13)
, видим, что ток и напряжение на резистивном элементе совпадают по фазе. (рис 3.12, 3.13)
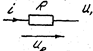

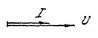
Рис 3.11 Рис 3.12 Рис 3.13
2) Индуктивный элемент. Параметр - индуктивность 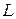 , (рис. 3.14). Пусть
, (рис. 3.14). Пусть 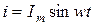 , тогда
, тогда 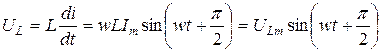 , здесь
, здесь 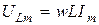 или
или 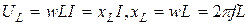 - индуктивное сопротивление (частотно-зависимое).
- индуктивное сопротивление (частотно-зависимое).
Вывод 2. На индуктивном элементе напряжение опережает по фазе ток на 90° (рис. 3.15, 3.16).
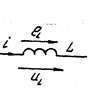
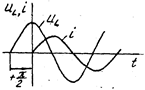

Рис 3.14 Рис 3.15 Рис 3.16
3) Емкостный элемент. Параметр- емкость 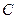 (рис. 3.17).
(рис. 3.17).
Пусть 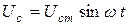 , тогда
, тогда 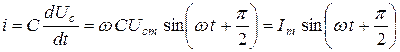 где
где 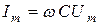 или
или 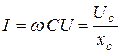 ; здесь
; здесь 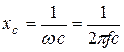 - ёмкостное сопротивление (частотно-зависимое).
- ёмкостное сопротивление (частотно-зависимое).
Вывод 3: Из сравнения начальных фаз 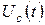 и
и 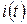 видим, что на ёмкостном элементе ток опережает по фазе напряжение на
видим, что на ёмкостном элементе ток опережает по фазе напряжение на 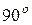 (Рис. 3.18, 3.19).
(Рис. 3.18, 3.19).
Последовательное соединение резистивного, индуктивного и ёмкостного элементов (Рис. 3.20). По II закону Кирхгофа имеем 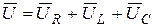 ; так как уравнение справедливо для векторов, строим векторную диаграмму (Рис. 3.21).
; так как уравнение справедливо для векторов, строим векторную диаграмму (Рис. 3.21).
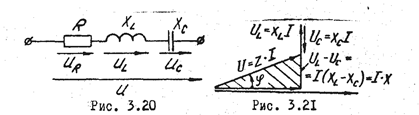
Начинаем с вектора тока  , общего для последовательно соединенных элементов. Далее выполняем построение по уравнению для
, общего для последовательно соединенных элементов. Далее выполняем построение по уравнению для  с учетом трех сделанных выше выводов. Пусть
с учетом трех сделанных выше выводов. Пусть 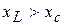 , тогда
, тогда 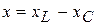 - реактивное сопротивление цепи.
- реактивное сопротивление цепи.
Если 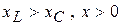 — цепь имеет активно—индуктивный характер и эквивалентна цепи рис. 3.22.
— цепь имеет активно—индуктивный характер и эквивалентна цепи рис. 3.22.
Если 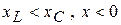 — цепь имеет активно—емкостный характер и эквивалентна цепи рис. 3.23.
— цепь имеет активно—емкостный характер и эквивалентна цепи рис. 3.23.

Если 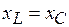 ,
, 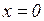 - цепь имеет число активный характер и эквивалентна цепи (рис. 3.24).
- цепь имеет число активный характер и эквивалентна цепи (рис. 3.24).
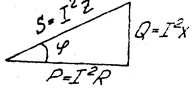
Заштрихованный треугольник на векторное диаграмме - треугольник напряжений. Если его стороны разделим на общий ток I, получим треугольник сопротивлений (рис. 3.25).

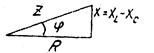
Рис. 3.24 Рис. 3.25
В нем 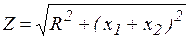 - полное сопротивление цепи последовательно соединенных элементов;
- полное сопротивление цепи последовательно соединенных элементов; 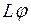 - угол сдвига по фазе между током и напряжением этой цепи, определяемый из
- угол сдвига по фазе между током и напряжением этой цепи, определяемый из 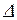 сопротивлений:
сопротивлений:
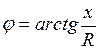

Рис. 3.26
Угол 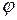 на векторной диаграмме отсчитывается от вектора тока к вектору напряжения. При этом
на векторной диаграмме отсчитывается от вектора тока к вектору напряжения. При этом 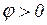 , если отсчет идет против часовой стрелки, и
, если отсчет идет против часовой стрелки, и 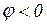 , если наоборот (рис. 3.26).
, если наоборот (рис. 3.26).
Закон Ома для цепи переменного тока: 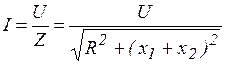
 Если стороны
Если стороны  напряжении умножить на общий
напряжении умножить на общий
ток I , получим треугольник мощностей (рис. 3.27)
в нем:
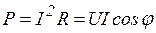 - активная мощность Вт;
- активная мощность Вт;
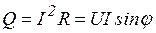 Рис. 3.27
Рис. 3.27
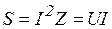 - полная мощность цепи,
- полная мощность цепи,  . Из
. Из  мощностей
мощностей 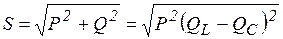 . Полная мощность цепи
. Полная мощность цепи 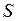 (участка цепи) измеряется с помощью амперметра и вольтметра, активная мощность
(участка цепи) измеряется с помощью амперметра и вольтметра, активная мощность 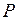 - с помощью ваттметра. Реактивная мощность
- с помощью ваттметра. Реактивная мощность 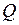 правило, вычисляется через найденные
правило, вычисляется через найденные 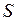 и
и 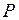 :
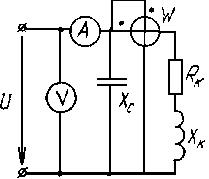
: 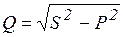 . Схема для измерения полной мощности
. Схема для измерения полной мощности 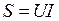 и активной мощности
и активной мощности 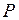 потребителя представлена на рис. 3.28.
потребителя представлена на рис. 3.28.
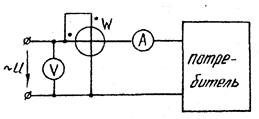
Рис. 3.28
Пример 3.2. Определить активную, реактивною и полную мощность 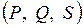 , для вышеуказанной цепи, а также эквивалентные пара метры потребители
, для вышеуказанной цепи, а также эквивалентные пара метры потребители 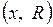 , если показание ваттметра 300 Вт, вольтметра 100 В, амперметра 5 А.
, если показание ваттметра 300 Вт, вольтметра 100 В, амперметра 5 А.
Решение. I) Ваттметр измеряет активную мощность потребителя, следовательно, Р = 300 Вт.
2) Вольтметр и амперметр фиксируют действующие значения напряжения U и тока I потребителя. Следовательно, полная мощность
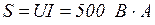
3) Из  мощностей потребителя (рис. 3.39) определяется реактивная мощность
мощностей потребителя (рис. 3.39) определяется реактивная мощность
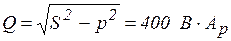
Рис. 3.29 Рис. 3.30
4) Полное сопротивление потребителя 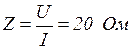
5) Активное сопротивление 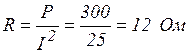
6) Реактивное сопротивление из 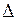 сопротивлений потребителя (рис. 3.30):
сопротивлений потребителя (рис. 3.30):
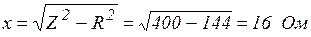
Примечание. 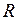 и
и 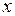 потребителя можно определить, используя выражения для мощностей
потребителя можно определить, используя выражения для мощностей 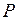 и
и 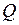 потребителя:
потребителя: 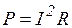 и
и 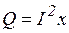
Применение комплексных чисел в расчете допей переменного тока. Данный метод позволяет заменить геометрические операции с векторами алгебраическими операциями с комплексными числами, соответствующими этим векторам. Представим синусоидальный ток 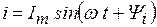 вращающимися векторами на декартовой плоскости, после чего формально совместим оси абсцисс и ординат соответственно с осями действительных и мнимых чисел комплексной плоскости (рис. 3.31). Тогда синусоидальный ток можно представить комплексным числом - точкой на комплексной плоскости, в которой лежит конец вектора I . Это комплексное число может быть выражено одной из следующих форм:
вращающимися векторами на декартовой плоскости, после чего формально совместим оси абсцисс и ординат соответственно с осями действительных и мнимых чисел комплексной плоскости (рис. 3.31). Тогда синусоидальный ток можно представить комплексным числом - точкой на комплексной плоскости, в которой лежит конец вектора I . Это комплексное число может быть выражено одной из следующих форм:
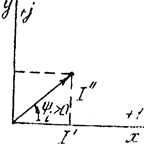
Рис. 3.31
а) алгебраической 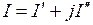
б) тригонометрической 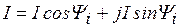
в) показательной 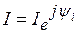 , где
, где 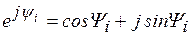 . В этих выражениях
. В этих выражениях 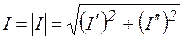
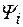 - начальная фаза тока, которая отсчитывается от положительного направления оси действительных чисел к вектору;
- начальная фаза тока, которая отсчитывается от положительного направления оси действительных чисел к вектору; 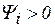 , если отсчет против часовой стрелки и
, если отсчет против часовой стрелки и 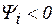 , если наоборот;
, если наоборот;
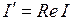 - действительная часть комплексного числа I;
- действительная часть комплексного числа I;
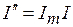 - мнимая часть комплексного числа I (точнее
- мнимая часть комплексного числа I (точнее 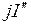 );
);
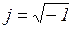 - мнимая единица;
- мнимая единица;
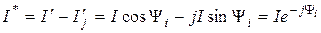 комплексное число, сопряженное с I;
комплексное число, сопряженное с I;
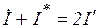 - действительное число;
- действительное число;
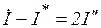 - мнимое число;
- мнимое число;
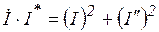 - квадрат модуля - действительное число.
- квадрат модуля - действительное число.
Пример 3.3. Напряжение 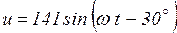 представить комплексным числом, записанным в формах а), б), в) и вектором на комплексной плоскости.
представить комплексным числом, записанным в формах а), б), в) и вектором на комплексной плоскости.
В показательной форме записи комплекс действующего значения напряжения 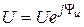 , где действующее напряжения
, где действующее напряжения 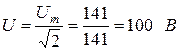 ,d начальная фаза
,d начальная фаза 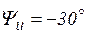 .
.
Ответ: алгебраическая 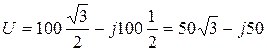 ;
;
тригонометрическая 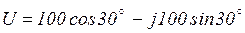 ;
;
показательная форма записи 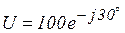 .
.
Векторное изображение напряжения см. на рис. 3.32.
Примем без доказательства каждому линейному соотношению между векторами соответствует такое же соотношение между комплексными числами, соответствующими этим векторам. Так для I закона Кирхгофа в цепи переменного тока (рис. 3.33) будут справедливы следующие выражения:
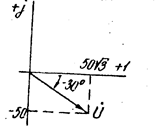
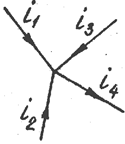
Рис. 3.32 Рис. 3.33
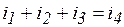 (для мгновенных значении),
(для мгновенных значении),
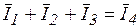 (для векторов действующих значений),
(для векторов действующих значений),
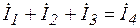 (для комплексов действующих значений).
(для комплексов действующих значений).
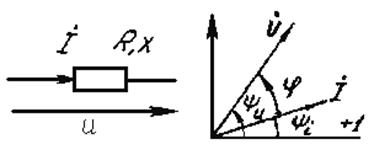 |
Комплексное сопротивление и преобразование схем. Пусть для участка цепи (рис. 3.34) имеем
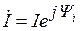 . На комплексной плоскости получим (рис. 3.33).
. На комплексной плоскости получим (рис. 3.33).
Рис. 3.34 Рис. 3.35
Образуем новое комплексное число
Из 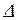 сопротивлений
сопротивлений 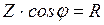 ;
; 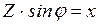
Окончательно полное комплексное сопротивление участка
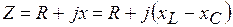 ; здесь
; здесь 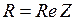 ;
; 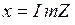 ;
;
полное сопротивление участка 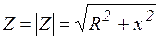 .
.
Пример 3.4. Записать полное комплексное сопротивление цепи на рис. 3.36. В соответствии с последней формулой получим
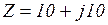
Пример 3.5. Определить для цепи на рис. 3.37.
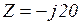 , так как
, так как 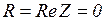 , а
, а 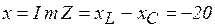
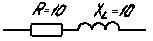 | 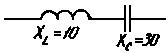 | ||
Рис. 3.36 Рис. 3.37
Использование комплексных сопротивлений облегчает преобразование схем, так как в этом случае справедливы все формулы преобразования цепей постоянного тока.
Пример 3.6. Участок 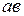 схемы на рис. 3.38 преобразовать в двухэлементный последовательный, если
схемы на рис. 3.38 преобразовать в двухэлементный последовательный, если 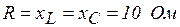 ;
;
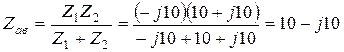 , т. е. В результате преобразования получим схему, представленную на рис. 3.39.
, т. е. В результате преобразования получим схему, представленную на рис. 3.39.
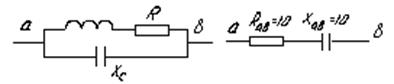 |
Рис. 3.38 Рис. 3.39
Комплексная мощность.
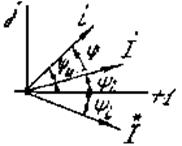 Пусть
Пусть 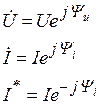
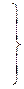 на комплексной плоскости (рис. 3.40)
на комплексной плоскости (рис. 3.40)
Полная комплексная мощность
Рис. 3.40 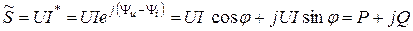 ,
,
т. е. Активная мощность 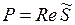 , а реактивная мощность
, а реактивная мощность 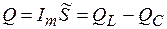 .
.
Пример 3.7. Определить активную, реактивную и полную мощность цепи, если известны 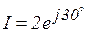 и
и 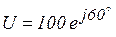 .
.
Решение: 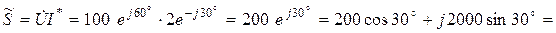
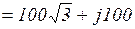 ;
; 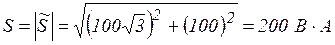
Ответ: 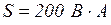 ,
, 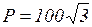 Вт;
Вт; 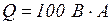 .
.
Понятие о проводимостях. Для участка цепи справедлива векторная диаграмма (рис. 3.41), где 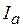 и
и 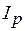 - активная и реактивная составляющие вектора тока;
- активная и реактивная составляющие вектора тока; 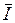 соответственно проекции вектора тока на направление вектора напряжения и на перпендикуляр к нему. Из диаграммы получим
соответственно проекции вектора тока на направление вектора напряжения и на перпендикуляр к нему. Из диаграммы получим 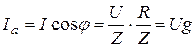 ,
,
где 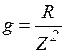 - активная проводимость;
- активная проводимость;
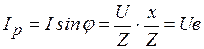 , где
, где
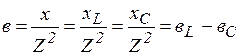 (
( 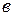 - реактивная,
- реактивная,
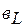 - индуктивная,
- индуктивная, 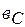 - емкостная проводимости);
- емкостная проводимости);
Рис. 3.41
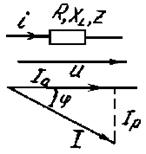
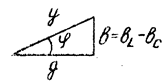
Рис. 3.42
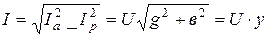
где 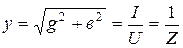 - полная проводимость (обратная полное сопротивлений). Проводимости ветви связаны друг с другом треугольником проводимостей (рис. 3.42).
- полная проводимость (обратная полное сопротивлений). Проводимости ветви связаны друг с другом треугольником проводимостей (рис. 3.42).
Резонансные режимы работы цепей возникают в цепях, содержащих индуктивные катушки и конденсаторы. Признак электрического резонанса - совпадение по фазе тока и напряжения цепи (участка цепи). Такая цепь ведет себя по отношению к источнику подобно резисторному элементу. Различают резонанс в последовательной и в параллельной цепи. Выявим условия, при которых возникают резонансы.
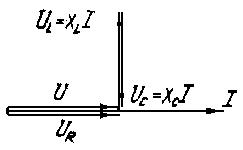 |
I. Резонанс напряжений возникает при последовательном соединении индуктивных катушек и конденсаторов (рис. 3.45). По II закону Кирхгофа
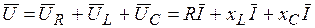 . В соответствии с этим уравнением и с учетом признаке резонанса получим векторную диаграмму (рис. 3.44), из которой следует, что
. В соответствии с этим уравнением и с учетом признаке резонанса получим векторную диаграмму (рис. 3.44), из которой следует, что 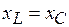 - условие резонанса напряжений или
- условие резонанса напряжений или 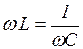 ,
, 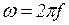 .
.
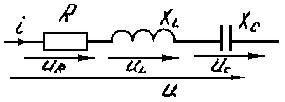 |
Рис. 3.43 Рис. 3.44
Следовательно, резонанс напряжений можно получить путем изменения значений любой из 3 величин: частоты 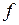 , индуктивности
, индуктивности 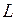 , емкости С. .
, емкости С. .
При резонансе напряжений ток в цепи достигает максимальных значений, так как полное сопротивление становится минимальным:
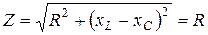 ,
, 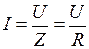 , напряжения на индуктивном и емкостном элементах одинаковы
, напряжения на индуктивном и емкостном элементах одинаковы 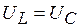 , а
, а 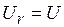 ; реактивная мощность цепи
; реактивная мощность цепи 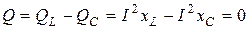 , следовательно, при резонансе активная и полная мощность одинаковы:
, следовательно, при резонансе активная и полная мощность одинаковы: 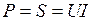 ,
, 
 резонансную частоту получим из условия резонанса напряжений
резонансную частоту получим из условия резонанса напряжений 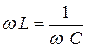 ;
; 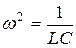 ;
; 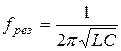
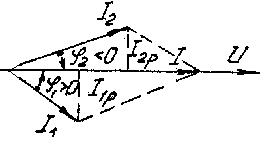
2. Резонанс токов возникает при параллельном соединении индуктивных катушек и конденсаторов (рис. 3.43). Для такой схемы 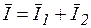 . Строим векторную диаграмму (рис. 3.46): начинаем с вектора напряжений
. Строим векторную диаграмму (рис. 3.46): начинаем с вектора напряжений 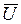 , являющегося общим для обеих ветвей, далее откладываем
, являющегося общим для обеих ветвей, далее откладываем 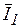 , отстающий от
, отстающий от 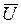 на
на 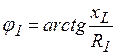 и
и 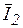 опережающий
опережающий 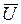 на
на  ; далее находим
; далее находим 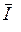
Очевидно, что признак резонанса - ток и напряжения должна бить в фазе - будет выполнен, если будут равны составляющие токов 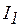 и
и 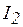 , т. е.
, т. е. 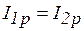 или
или 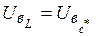 , тогда условием резонанса токов будет равенство реактивных проводимостей:
, тогда условием резонанса токов будет равенство реактивных проводимостей:
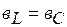 или
или 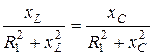 , где
, где 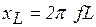 ,
, 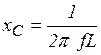 ,
, 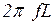 ;
;
 |
как видно из формул, резонанс токов можно получить изменением любой из пяди величин:
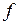 ,
, 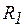 ,
, 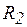 ,
, 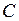 ,
, 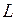 .
.
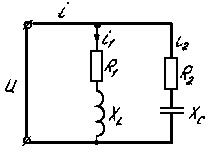 |
Рис. 3.45 Рис. 3.46
При резонансе напряжений 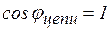 (признак резонанса) реактивная мощность Q = 0 (если умножить уравнение * - на общее напряжение
(признак резонанса) реактивная мощность Q = 0 (если умножить уравнение * - на общее напряжение 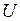 , то
, то 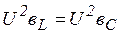 , т. е.
, т. е. 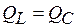 ,
, 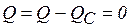 ) и активная мощности цепи численно уравниваются:
) и активная мощности цепи численно уравниваются: 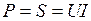 .
.
 |
Пример 3.8. Определить показания ваттметра, если вольтметр и амперметр соответственно показали 100 В и 2 А. В цепи (рис. 3.47) резонансный режим.
Рис. 3.47
Решение. Ваттметр измеряет активную мощность (по схеме - на катушке); так как в данном случае других потребителей активной мощности, кроме  , в схеме нет, то ваттметр измерит активную мощность всей цепи.
, в схеме нет, то ваттметр измерит активную мощность всей цепи.
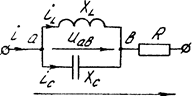
Рис. 3.48
но при резонансе 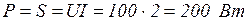
Ответ: показание ваттметра 200 Вт.
Пример 3.9. Определить ток источника 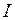 , если
, если 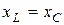 (рис. 3.48).
(рис. 3.48).
Решение. Строим векторную диаграмму (рис. 3.49). Индуктивный и емкостный элементы включены на одно напряжение 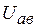 , токи в них по значению одинаковы:
, токи в них по значению одинаковы: 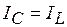 . Построение векторной диаграммы при смешенном соединении элементов удобно начинать с вектора напряжения на параллельном участке (
. Построение векторной диаграммы при смешенном соединении элементов удобно начинать с вектора напряжения на параллельном участке ( 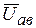 ), далее наносим
), далее наносим 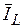 и
и 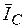 - они в противофазе, следовательно
- они в противофазе, следовательно 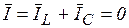 .
.
Ответ: ток источника 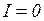
Такая цепь не пропускает ток данной частоты. Если частота изменится, то появится ток ( 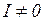 ).
).
Вопросы для самопроверки
1. Какой ток называется переменным?
2. Что такое период, частота, начальная фаза?
3. Как определить начальную фазу синусоидальной величины на временном графике, векторной диаграмме?
4. Каким образом может быть задана синусоидальная величина?
5. Каковы разовые соотношения между током и напряжением на резистивном, индуктивном и емкостном элементах?
6. Привести выражения для индуктивного, емкостного и полного сопротивления. Как изображается 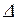 сопротивлений?
сопротивлений?
7. Чем отличается в записи закон Ома и законы Кирхгофа в цепи синусоидального тока от записи для цепи постоянного тока?
8. Привести выражения для реактивной, активной и полной мощностей в цепи синусоидального тока. Как изображается 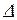 мощностей?
мощностей?
9. Как записать полное комплексное сопротивление ветви?
10. Как определить полную комплексную мощность цепи, а также активную и реактивную мощности по заданным комплексным напряжению и току цепи?
11. Что является признаком электрического резонанса?
12. Каковы условия резонанса напряжения и токов?
13. Изменением каких параметров можно добиться резонанса напряжений и резонанса токов?
14. Каковы характерные свойства цепей, настроенных в резонансе?
Дата: 2018-12-21, просмотров: 699.