Данные цепи - совокупность трехфазного источника синусоидально и ЭДС и соединенных с ним потребителей, как однофазных, так и трехфазных. Источник трехфазной системы позволяет получить одинаковые по амплитуде и частоте ЭДС в каждой из трех обмоток (фазах) источника. Важно, что эти ЭДС сдвинуты по фазе относительно друг друга на 120° (рис. 4.1). Три обмотки (фазы) генератора соединяются в заезду (Y) или в звезду с нейтралью . (Y). Соответственно образуются трех- и четырехпроводные трехфазные цепи (рис. 4.2, 4.5); нейтраль соединяет общие точки источнике и нагрузки. Если пренебречь внутренний сопротивлением фаз источника, то напряжения на фарах источника - фазные напряжения равны ЭДС фаз: 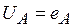 ,
, 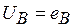 ,
, 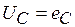
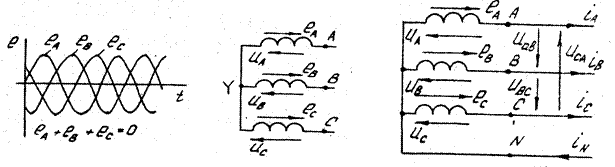
Рис. 4.1 Рис. 4.2 Рис. 4.3
Тогда в соответствии с представленной временной диаграммой 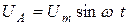 ,
, 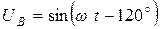 ,
, 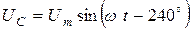 . Фазные напряжения в виде вращающихся векторов на декартовой и комплексной плоскостях показаны на рис. 4.4 и 4.5. Напряжения между точками А, В, С (между линейными проводами) называются линейными напряжениями
. Фазные напряжения в виде вращающихся векторов на декартовой и комплексной плоскостях показаны на рис. 4.4 и 4.5. Напряжения между точками А, В, С (между линейными проводами) называются линейными напряжениями 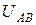 ,
, 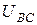 ,
, 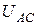 . Очевидно, что
. Очевидно, что 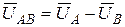 ,
, 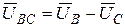 ,
, 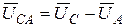 . Из векторной диаграммы
. Из векторной диаграммы 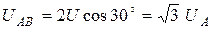 , т.е. при соединении фаз генератора в Y или в
, т.е. при соединении фаз генератора в Y или в 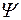 линейное напряжение превышает фазное в
линейное напряжение превышает фазное в 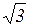 раз;
раз; 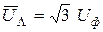 .
.
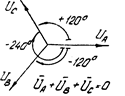
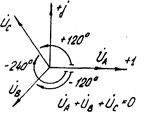
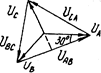

Рис. 4.4 Рис. 4.5 Рис. 4.6 Рис. 4.7
Потребители в трехфазных цепях могут образовывать симметричною и несимметричную нагрузку. Симметричная нагрузка 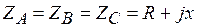 - полные комплексные сопротивления фаз потребителя равны. Симметричную нагрузку могут образовывать только трехфазные потребители (например, трехфазные двигатели). Однофазные потребители (лампы накаливания) нагреватели, однофазные двигатели и т.д.) образуют несимметричную нагрузку.
- полные комплексные сопротивления фаз потребителя равны. Симметричную нагрузку могут образовывать только трехфазные потребители (например, трехфазные двигатели). Однофазные потребители (лампы накаливания) нагреватели, однофазные двигатели и т.д.) образуют несимметричную нагрузку.
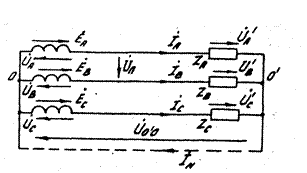 Соединение потребителей в звезду. Из схемы на рис. 4.8 видно, что при соединении в Y линейный ток равен току в фазе нагрузки:
Соединение потребителей в звезду. Из схемы на рис. 4.8 видно, что при соединении в Y линейный ток равен току в фазе нагрузки: 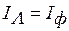 .
.
Рис. 4.8
По II закону Кирхгофа
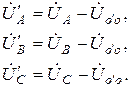
где 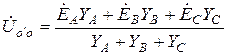
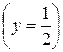
Если 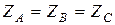 , то
, то 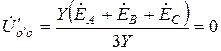 , тогда
, тогда 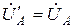 ,
, 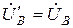 ,
, 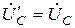 , т. е. Напряжения на фазах симметричной нагрузки равны фазным напряжениям источника,
, т. е. Напряжения на фазах симметричной нагрузки равны фазным напряжениям источника, 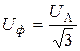 (см. рис. 4.6).
(см. рис. 4.6).
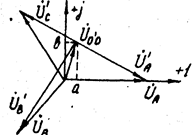
Рис. 4.9
Если нагрузка несимметричная, т.е. 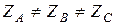 , то
, то 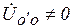 . Пусть, например,
. Пусть, например, 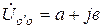 . Найдем напряжения на фазах нагрузки с помощью системы уравнений, составленных по II закону Кирхгофа, и векторной диаграммы на комплексной плоскости, положив
. Найдем напряжения на фазах нагрузки с помощью системы уравнений, составленных по II закону Кирхгофа, и векторной диаграммы на комплексной плоскости, положив 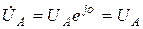 (рис. 4.9).
(рис. 4.9).
Из векторной диаграммы видно, что напряжения 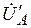 ,
, 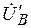 ,
, 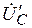 резко отличаются по значению. Это недопустимо. Причиной такого "перекоса" фазных напряжений потребителей являлось напряжение
резко отличаются по значению. Это недопустимо. Причиной такого "перекоса" фазных напряжений потребителей являлось напряжение 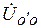 . Как устранить "перекос"?. Соединим общие точки 0’ и 0 четвертым проводом - нейтралью с пренебрежимо малым, со противлением
. Как устранить "перекос"?. Соединим общие точки 0’ и 0 четвертым проводом - нейтралью с пренебрежимо малым, со противлением 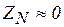 (см. пунктир), тогда
(см. пунктир), тогда 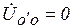 и вновь
и вновь 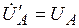 и т.д. Очевидно, что при наличии нейтрали напряжение на фазах потребителей
и т.д. Очевидно, что при наличии нейтрали напряжение на фазах потребителей 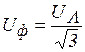 даже при несимметричной нагрузке. Ток в нейтрали определяется в соответствии с уравнениями
даже при несимметричной нагрузке. Ток в нейтрали определяется в соответствии с уравнениями 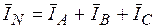 (находится непосредственно по векторной диаграмме) или
(находится непосредственно по векторной диаграмме) или 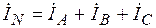 и определяется после нахождения токов в фазах нагрузки:
и определяется после нахождения токов в фазах нагрузки:
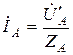 ,
, 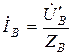 ,
, 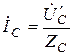
где: 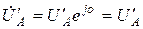 ,
, 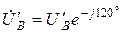 ,
, 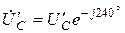 и
и 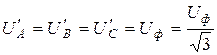
В четырехпроводной цепи потребители можно включать между линейными проводами (рис. 4.10) - на линейное напряжение 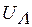 (потр
(потр 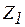 ), а также между линейным проводом и нейтралью - на фазное напряжение
), а также между линейным проводом и нейтралью - на фазное напряжение 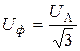 (потр
(потр 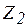 ). Таким образом проводная цепь позволяет использовать потребители с различным номинальным напряжением (например, 380 В и 220 В).
). Таким образом проводная цепь позволяет использовать потребители с различным номинальным напряжением (например, 380 В и 220 В).
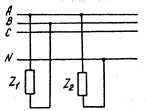
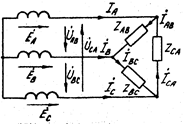
Рис. 4.10 Рис. 4.11
Соединение потребителей в треугольник ( 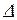 ) производится по принципу: конец 1-й фазы с началом 2-й, конец 2-й с началом 3-й и конец 3-й с началом 1-й (рис. 4.11). Из схемы видно, что при соединении потребителей треугольником
) производится по принципу: конец 1-й фазы с началом 2-й, конец 2-й с началом 3-й и конец 3-й с началом 1-й (рис. 4.11). Из схемы видно, что при соединении потребителей треугольником 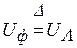 . Определение токов в цепи:
. Определение токов в цепи:
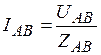 ,
, 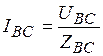 ,
, 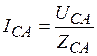 (4.1)
(4.1)
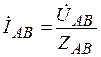 ,
, 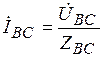 ,
, 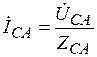 (4.2)
(4.2)
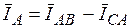 ,
, 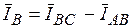 ,
, 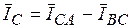 (4.3)
(4.3)
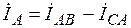 ,
, 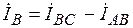 ,
, 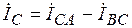 (4.4)
(4.4)
 а) Нагрузка симметричная:
а) Нагрузка симметричная: 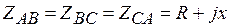 . Определим
. Определим 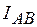 ,
, 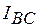 ,
, 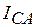 по формулам (4.1). Все они отстают от "своих" напряжений
по формулам (4.1). Все они отстают от "своих" напряжений 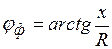 . Линейные токи определим из векторной диаграммы (рис. 4.12) с помощью формул (4.3). Из диаграммы
. Линейные токи определим из векторной диаграммы (рис. 4.12) с помощью формул (4.3). Из диаграммы 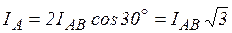 т.е. при соединении симметричных потребителей в
т.е. при соединении симметричных потребителей в 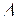 линейный ток в
линейный ток в 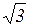 раз больше фазного,
раз больше фазного, 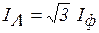 .
.
Рис. 4.12 Рис. 4.13
б) Несимметричная нагрузка: 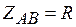 ;
; 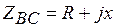 ;
; 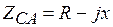 . Фазные токи по-прежнему определяются по формулам (4.1). Линейные токи получим либо из векторной диаграммы на рис. 4.13, либо по формулам.(4.4) и (4.2), где
. Фазные токи по-прежнему определяются по формулам (4.1). Линейные токи получим либо из векторной диаграммы на рис. 4.13, либо по формулам.(4.4) и (4.2), где 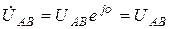 ,
, 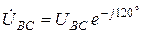 ,
, 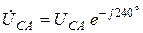 и
и 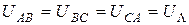 .
.
Мощности в трехфазных цепях. Независимо от способа соединения потребителей (Y или 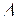 ) при симметричной нагрузке мощность ее равна утроенной мощности одной фазы:
) при симметричной нагрузке мощность ее равна утроенной мощности одной фазы:
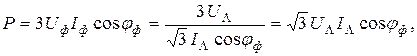 аналогично
аналогично
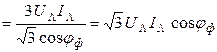 .
.
При несимметричной нагрузке отдельно определяются активная и реактивная мощности каждой фазы» тогда мощность цепи
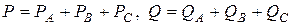 ,
, 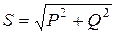
Измерение модности в трехфазной цели.
1. При симметричной нагрузке применяется метод одного ваттметра (рис. 4.14), т.е. измеряется активная мощность одной фазы и результат утраивается: 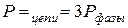
2. Метод двух ваттметров (схема Арона, рис. 4.15) позволяет определить мощность нагрузки (симметричной и несимметричной) при любом способе соединения фаз:
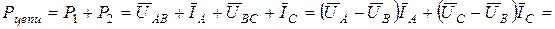
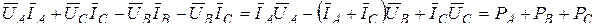 так как
так как 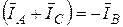
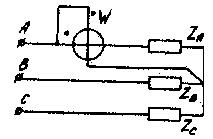 |
Рис. 4.14
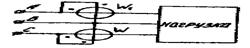 |
5. В четырехпроводной цепи применяется метод трех ваттметров (рис. 4.16):

Рис. 4.15 Рис. 4.16
Вопросы для самопроверки
1. Какие электрические цепи называются трехфазными?
2. Можно ли в трехфазные цепи включать однофазные потребители? Если можно, то как - между линейными проводами или одним из линейных проводов и нейтралью? От чего это зависит?
5. Что такое линейное и фазное напряжения, линейный и фазный токи? Показать на схемах их положительные направления при соединении потребителей звездой, треугольником.
4. Какая нагрузка в трехфазной цепи называется симметричной?
5. Каково соотношение между фазными и линейными напряжениями симметричного потребителя при соединении звездой?
6. Каково соотношение между фазными и линейными токами симметричного потребителя при соединении треугольником?
7. чем объяснить наличие четвертого (нейтрального) провода в трехфазных цепях?
8. Почему в нейтраль не включают предохранители?
9. Как определить ток в нейтрали?
10. Как определить полную мощность трехфазной цепи при заданном количестве потребителей, однофазных и трехфазных?
11. Сколько ваттметров и как нужно включить для измерения активной мощности симметричного трехфазного потребителя?
12. В чем сущность метода двух ваттметров? Можно ли использовать этот метод в четырехпроводных цепях?
15. Сколько ваттметров и как нужно включить, чтобы измерить активную мощность несимметричной нагрузки в четырехпроводной цепи?
14. Каков порядок построения векторной диаграммы при соединении симметричного потребителя звездой, треугольником?
Дата: 2018-12-21, просмотров: 645.