Рассмотрим электромагнитный процесс в идеализированной катушке (пренебрегаем активным сопротивлением ее обмотки и не учитываем потери энергии в сердечнике).

Т.к. μ ферромагнитных материалов не постоянна, то зависимость Ф(i) -не линейна. Поэтому индуктивность катушки с сердечником изменяется в зависимости от тока.

Рис.12 Кривые потока Ф(i) и тока i(t) в цепи со сталью.

Кривая тока несинусоидальна, при этом магнитный поток отстает по фазе от тока (δ). В составе гармоник тока особенно выделяется третья гармоника.

При синусоидальном токе в обмотке катушки магнитный поток, ЭДС и напряжение будут несинусоидальные.(Рис.13)

Рис.13

Кривая магнитного потока(Ф) – близка к трапеции , кривые напряжения и ЭДС имеют более заостренную форму, чем синусоида и находятся в противофазе.Магнитный гистерезис еще больше искажает форму кривой тока.

ВАХ катушки с ферромагнитным сердечником снимается при синусоидальном напряжении на выходах катушки (Рис.14).

ОА– ненасыщенное состояние катушки (i и u синусоидальное)

АВ– насыщение состояние катушки (i несинусоидальное).

Рис.14 ВАХ катушки с ферромагнитным сердечником.

Магнитное поле в сердечнике непрерывно изменяется. Часть энергии магнитного поля превращается в тепло и называется мощностью потерь в стали.

,где P_г зависит от гистерезиса , а P_в - от вихревых токов.

,где σ_г – коэффициент гистерезиса, зависящий от материала;

f– частота;

В_m- амплитуда магнитной индукции;

n – степень (при В_m=0,1–1 Тл ; n=1,6 , а при В_m =1–1,6 Тл ; n=2).

 (оказывает размагничивающее действие) , где σ_в – коэффициент, зависящий от материала сердечника и квадрата толщины листов, из которых собран сердечник (при f=50 Гц , толщина 0,35–0,5 мм , а при f=400 Гц , толщина 0,1–0,35 мм.).

Потери в обмотке (потери в меди)

, где R–активное сопротивление обмотки.

Активная мощность катушки расходуется на покрытие потерь.

;

Катушка служит основной частью многих электрических машин и аппаратов. В качестве материала сердечника используют электротехническую сталь или специальные ферромагнитные материалы (ферриты, пермаллои и т.д...).

а)                          б)

Рис.15 Катушка с ферромагнитным сердечником (а) и упрощённая векторная диаграмма (б).

– приложенное напряжение, ЭДС должно быть синусоидальным, т.к. Ф=Ф_msin(ωt);

Активное сопротивление катушки и потоки рассеяния незначительны.

Рис.16

Кривая тока i(t) несинусоидальная. Реальную кривую можно заменить эквивалентной синусоидой.

Электрическая схема цепи с учетом потока рассеяния (Ф_σ >0).потерь в обмотке (R_к>0) и потерь на перемагничивание сердечника (Рис.17,а).

а)                                   б)

Рис.17 Схема замещения (а) и полная векторная диаграмма (б) катушки с ферромагнитным сердечником.

-уравнение электрического состояния катушки с ферромагнитным сердечником.

Практическое применение катушки с ферромагнитным сердечником. Катушка индуктивности с ферромагнитным сердечником, имеющим воздушный зазор, называется дросселем. Дроссель используется как индуктивное сопротивление в электрических цепях и фильтрах. Изменяя воздушный зазор, можно регулировать ток в электрической цепи переменного тока (усилители мощности в схемах радиотехники, автоматики, электроизмерительной и вычислительной технике)

Индуктивное сопротивление создаваемое катушкой с замкнутым ферромагнитным сердечником можно изменять подмагничиванием сердечника с помощью дополнительной обмотки, подключаемой к регулируемому источнику постоянного напряжения. Изменяя подмагничивающий постоянный ток I , можно регулировать в широком диапазоне переменный ток i. Это свойство используют в магнитных усилителях (МУ).

Рис.18 Простейший магнитный усилитель.

Основными элементами МУ являются два замкнутых одинаковых магнитных сердечника с несколькими обмотками:

-обмотка переменного тока (рабочая);

-несколько обмоток постоянного тока (управление, смещение, обратной связи).

Рис.19 МУ переменного тока.

Магнитные усилители характеризуются коэффициентами усиления по току , напряжению и мощности.

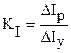- коэффициент усиления по току.

- коэффициент усиления по напряжению.

- коэффициент усиления по мощности.

У обычных магнитных усилителей коэффициенты усиления по току и напряжению (К_I и К_U) достигают нескольких десятков , а коэффициент усиления по мощности (К_P) – сотни и более.

МУ обладают большой инертностью. Она характеризуется постоянной времени цепи управления.

 , где R_y  -активное сопротивление , t_пер=5t.

 , где h- КПД,  f- частота.

Электрическая цепь, содержащая последовательно или параллельно соединенные: катушку индуктивности и линейный конденсатор, образует нелинейный колебательный контур. Такой контур является составной частью многих электротехнических устройств: ферромагнитных стабилизаторов, преобразователей частоты, усилителей, устройств автоматики, телемеханики, вычислительной техники.

Участки электроэнергетических систем (линий электропередач – трансформаторы) также могут быть нелинейными колебательными контурами. Явление , наблюдаемое в таких цепях, называется феррорезонансном.

В нелинейном колебательном контуре под воздействием синусоидальной ЭДС (напряжения) с частотой ω могут возникать резонансные явления на высших (nω), низших (ω/m) и дробных гармониках (nω/m).

В контуре при наступлении или исчезновении резонанса возникают скачки амплитуды тока (и напряжения). Резонансная частота нелинейного контура  не остается постоянной, т.к. L зависит от I.

а)                                        б)

Рис.20 Резонансные кривые тока в линейном (а) и в нелинейном (б) колебательном контуре.

Если ω↑ÞI_m↑Þω_p↑ ; при ω_р=ω, I_m=max ; при ω_р>ω, I_m–уменьшается , т.к. I_m↓Þω_p↓Þ(ω_p–ω)↓ÞI_m↓↓.

В контуре произойдет уменьшение скачком I_m и установятся колебания с малой амплитудой (w=w₁). Если после скачка I_m  уменьшать частоту ЭДС ω, то I_m и ω_р будут возрастать. При достаточном сближении ω и ω_р наступит самонаростающий процесс обратного скачка I_m от малых величин к большим(w=w₂).

Феррорезонансном напряжений называют электрический резонанс в цепи , состоящий из последовательно соединенных нелинейной катушки индуктивности и линейного конденсатора.

Простейшая цепь, в которой возможен феррорезонанс напряжений, показана на Рис.21(а). На Рис.21(б) показаны вольтамперные характеристики нелинейной индуктивности U_L(I) и линейной ёмкости U_C(I) ,а также теоретическая ВАХ всей цепи U(I).

а)                          б)                                        в)

Рис.21 Феррорезонанс напряжений.

Если R=0, то U=|U_L–U_C|.В точке I_P (Рис.21,б) U_L=U_C , т.е. в цепи наблюдается резонанс , при I<I_P→U_L>U_C , а при I>I_P→U_L<U_C

Из-за активного сопротивления цепи и высших гармоник в кривых напряжений и тока действительноя ВАХ отличается от теоретической(Рис.21,в). При плавном увеличении U от 0 до U_а ток в цепи плавно возрастает до I_а. Дальнейшее незначительное увеличение U сопровождается скачком тока до I_b. После скачка дальнейшее повышение U будет сопровождаться плавным возрастанием тока. При плавном уменьшении U до U_C ток плавно уменьшается до I_C. Затем незначительное уменьшение U вызывает уменьшение тока скачком до I_d. Скачки сопровождаются изменением угла сдвига фаз между напряжением на выходах цепи и током.

Феррорезонансом токов называют резонанс в цепи, состоящей из параллельно соединенных нелинейной катушки индуктивности и линейного конденсатора. Простейшая цепь, в которой возможен феррорезонанс токов, показана на Рис.22(а).

а)                                   б)                                        в)

Рис.22 Феррорезонанс токов.

U_L=U_C=U – напряжение на выводах катушки.

I=|I_L–I_C|  - ток  в неразветвлённой части цепи.

При I_L=I_C наступает феррорезонанс токов. На Рис.22(б) по заданным ВАХ катушки I_L(U) и конденсатора I_C(U) построена теоретическая ВАХ всей цепи I(U). Реальная ВАХ (Рис.22,в) строится с учётом высших гармоник и активной сопротивляющей тока в цепи. В рассматриваемой цепи одному и тому же значению тока I в неразветвленной части цепи могут соответствовать три различных значения напряжения на выводах контура; два из них соответствуют устойчивым режимам работы цепи е-а ; d–в , а одно–неустойчивому а–d. Неустойчивые режимы можно сделать устойчивыми, если плавно регулировать не ток, а напряжение на нелинейном контуре.

Для нормальной работы некоторых приемников необходимо поддерживать напряжение на их выводах  неизменным при изменении напряжения в питающей сети. С этой целью применяются различные устройства, называемые стабилизаторами напряжения.

Принцип работы простейшего феррорезонансного стабилизатора напряжения основан на явлении феррорезонанса напряжений, а у большинства стабилизаторов – феррорезонанса токов.

а)                          б)

Рис.23 Простейший феррорезонансный стабилизатор напряжения.

Рабочая часть ВАХ нелинейной катушки должна находиться в области насыщения. Емкость С подбирается так, чтобы использовав явление феррорезонанса получить большой ток в катушке, т.к. U_C и U_L=U_вых сдвинуты по фазе примерно на 180˚, то U_вых≈U_C–U_L.В данном случае не учитывается активное сопротивления и высшие гармоники напряжений и токов. Выберем два произвольных значения тока:I₁ и I₂. Видно , что разность ∆U_ВХ=U_ВХ2-U_ВХ2 , значительно больше , чем разность ∆U_ВЫХ=U_ВЫХ2–U_ВЫХ. Т.е. при значительных изменениях напряжение на входе, напряжение на выходе изменяется незначительно. Схема работает как стабилизатор напряжения. Для повышения стабилизирующего эффекта, увеличения КПД и шунтирования высших гармоник применяют более сложные схемы (Рис.24).

Рис.24 Стабилизатор напряжения.

Др1–линейный элемент (катушка с ненасыщенным магнитопроводом)

Др2 и С–нелинейный элемент (резонансный контур, ДР2 катушка с насыщенным магнитопроводом)

Резисторы как линейные элементы в стабилизаторах не используются, т.к. это привело бы к существенному увеличению тепловых потерь.