Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Определение 1.

Параболоидом вращения называется поверхность, образованная вращением параболы вокруг ее оси симметрии.

Получим поверхность, вращая кривую 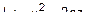 – параболу, вокруг оси 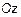. Согласно правилу, уравнение поверхности будет иметь вид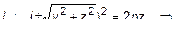 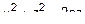 или

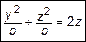 .                         (1)

Если параболоид вращения деформирован сжатием или растяжением в области кругового сечения, то получится эллиптический параболоид

119

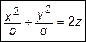 .                                 (2)

Данные поверхности изображены на рис. 1.

Гиперболический параболоид

Исследуем методом сечений поверхность

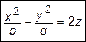 .                                      (3)

1. Сечение плоскостью 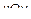, т. е. , тогда

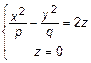или 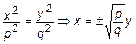 – две прямые.

Cделаем сечение плоскостью 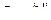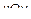. Тогда  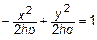– гипербола.

2. Сечение плоскостью 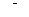, т. е. 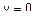, тогда

или 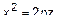 – парабола.

3. Сечение плоскостью 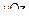, т. е. , тогда

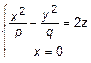или 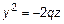 – парабола.

Дополнительно сделаем сечение плоскостью 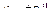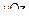. Тогда  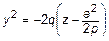- парабола. Т. к. в сечениях две параболы, одна гипербола, следовательно, это гиперболический параболоид рис. 2.

120

2. Цилиндрические поверхности

Определение 2.

Цилиндрической поверхностью называется поверхность, образованная движением прямой (образующей), параллельно самой себе и пересекающей заданную линию (направляющую).

Пусть l – образующая прямая 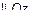, L – направляющая, заданная в плоскости 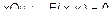. Тогда поверхность будет иметь вид рис. 3. Возьмем на поверхности некоторую точку 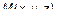. Очевидно 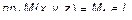. Следовательно, обе точки имеют одинаковые координаты x, y и при этом в не зависимости от координаты z. Следовательно, уравнение направляющей есть уравнение цилиндрической поверхности, если оно рассматривается относительно координат в пространстве

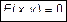.      (4)

При этом образующая цилиндра будет параллельна оси координат одноименной с отсутствующей переменной.

В зависимости от вида направляющей различают такие цилиндрические поверхности:

а) параболический цилиндр рис. 4; б) круговой цилиндр рис. 5;

в) эллиптический цилиндр рис. 6; г) гиперболический цилиндр рис. 7.

 

121

3. Конические поверхности.

Определение 3.

Конической поверхностью называют поверхность, образованную движением прямой (образующей), проходящей через заданную точку (вершину) и пересекающей заданную линию (направляющую).

Пусть l – образующая прямая, L – направляющая, О – вершина. Тогда поверхность будет иметь вид рис. 8.

В частном случае коническая поверхность может быть образовании вращением некоторой прямой 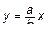 вокруг оси 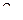. При этом согласно правилу построения поверхностей вращения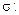

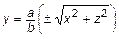
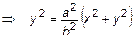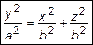 или  . (5)

Уравнение (5) есть уравнение прямого кругового конуса. Исследуем эту поверхность методом сечений

1. Сечение плоскостью 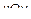, т. е. , тогда

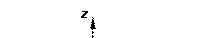
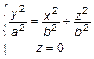       или 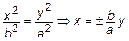 – две прямые.

2. Сечение плоскостью 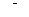, т. е. 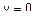, тогда

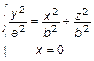       или 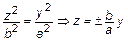 – две прямые.

3. Сечение плоскостью 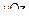, т. е. , тогда

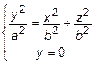       или 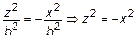 – точка начала координат.

Дополнительно сделаем сечение плоскостью 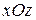. Тогда  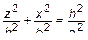или 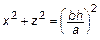  – окружность. Поверхность изображена на рис. 9.

Заключение

122

Данной лекцией закончена тема «Аналитическая геометрия». Однако на протяжении всего курса математики необходимо будет возвращаться к ней. Например, при изучении темы «Функции многих переменных» и др. В последних двух лекциях рассмотрены основные типы поверхностей, встречающиеся в прикладных задачах. Однако это лишь небольшая минимально необходимая часть сведений о поверхностях.

Отметим следующее:

- существуют прямые полностью лежащие на поверхности гиперболического параболоида;

- при деформации поверхности вращения, в конечном уравнении коэффициенты при переменных различны;

- существуют и не прямые конические поверхности;

- рассматривая уравнение плоской кривой второго порядка относительно пространственных координат, получим уравнение цилиндра.

- цилиндр имеет бесконечную длину.

Литература

1. Бермант А.Ф. и др. Краткий курс математического анализа. – М.: Высшая школа, 2001.

2. Рыжков В. В. Лекции по аналитической геометрии. – М.: Факториал пресс, 2000, – 208 с.

3. Ефимов Н.В. Краткий курс аналитической геометрии. – М.: Физматлит, 2002.

4. Шипачев В.С. Основы высшей математики. - М.: Высшая школа,1998.

5. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. – М.: Наука, 1989,  – 659 с.

123

Предметный укозатель

Наименование

Стр.
Ал-Каши	5
Алгебраическое дополнение	54
Аристотель	4
Архимед	5
Базис операций	19
Базис пространств	44
Биекция	30
Бинарные отношения	23
Вектор	39
Вектор единичный	40
Вектора коллинеарные	39
Вектора компланарные	39
Вектора линейно-зависимые	41
Вектора противоположны	39
Векторное произведение	54
Вершина эллипса	101
Вершины гиперболы	105
Гаусс К. Ф.	6
Гильберт	7
Гипербола	103
Гиперболоид	115
Декарт Рене	6
Декартов базис	45
Дирихле	6
Дополнение множества	18
Инъекция	30
Каноническое уравнение гиперболы	104
Каноническое уравнение параболы	108
Каноническое уравнение прямой	86
Каноническое уравнение эллипса	100
Квантор	9
Континиум	34
Коническая поверхность	121
Коши Огюстен-Луи	6
124 Лейбниц Генрих	6
Леонардо да Винчи	5
Линия	97
Лобачевский Н. И.	7
Ляпунов А.М.	7
Марков А.А.	7
Матрица	60
Матрица диагональная	63
Матрица квадратная	53
Матрица обратная	62
Матрица столбец	61
Матрица транспонированная	61
Матричный метод	71
Метод Жордана-Гаусса	74
Метод Крамера	71
Метод сечений	114
Минор	54
Множества конечные	33
Множества эквивалентные	23
Множество	8
Множество бесконечное	11
Множество действительных чисел	10
Множество конечное	11
Множество натуральных чисел	10
Множество пустое	10
Множество рациональных чисел	10
Множество счетное	33
Множество универсальное	18
Множество целых чисел	10
Мощность множества	11, 32
Норма	38
Ньютон Исаак	6
Обратная функция	31
Обратное отношение	27
Общее уравнение плоскости	78
Объединение множеств	14
125 Окружность	98
Определенная система	70
Определитель матрицы	53
Отношение эквивалентность	24
Отношения множеств	20
Парабола	107
Параметрическое уравнение прямой	86
Параболоид	118
Пересечение множеств	15
Плоскость	78
Поверхность	77
Подмножество	12
Подмножество несобственное	13
Поле	37
Полуось эллипса	101
Полярная система координат	47
Преобразование координат	65
Преобразование матриц	65
Проекция	45
Произведение множеств	19
Произведение матриц	62
Пространства линейные	37
Пространства нормированные	38
Прямая	85
Прямая на плоскости	91
Радиус-вектор	46
Разность множеств	16
Ранг матрицы	65
Рефлексивность	24
Риман	6
Связное отношение	26
Симметрическая разность	16
Симметричность	24
Скалярное произведение	49
Смешанное произведение	58
Совместная система	70
126 Соответствие	21
Сумма векторов	39
Сумма матриц	61
Суперпозиция	26
Сюръекция	30
Теорема де-Моргана	18
Теорема Кронекера-Капелли	72
Теорема Лапласа	54
Транзитивность	24
Угол между векторами	52
Угол между прямыми на плоскости	93
Угол между плоскостями	83
Угол между прямыми в пространстве	88
Угол прямой с плоскостью	88
Унарные отношения	20
Уравнение линии	97
Уравнение плоскости в отрезках	81
Уравнение плоскости через 3 точки	82
Уравнение прямой в отрезках	92
Уравнение прямой с угловым коэффициентом	93
Уравнение прямой через 2 точки	86
Фибоначчи Леонардо Пизанский	5
Фокус гиперболы	104
Фокус эллипса	99
Фундаментальное решение	74
Функционал	38
Функция на множестве	29
Цилиндрическая поверхность	120
Чебышев П.Л.	7
Эвклид	4
Эвклидово пространство	49
Эйлер Леонард	6
Эксцентриситет гиперболы	106
Эксцентриситет эллипса	102
Эллипс	99

127

Греческий алфавит

                   

128

Содержание

 

Предисловие	3
Краткая историческая справка	4
Лекция № 1 «Множества»	8
Лекция № 2    «Алгебра множеств»	14
Лекция № 3   «Отношения множеств»	22
Лекция № 4   «Функции множеств»	29
Лекция № 5   «Линейные пространства»	36
Лекция № 6   «Векторная алгебра»	41
Лекция № 7   «Эвклидово пространство»	48
Лекция № 8   «Определитель»	53
Лекция № 9   «Матрицы»	60
Лекция № 10  «Системы уравнений»	69
Лекция № 11 «Плоскость в пространстве»	77
Лекция № 12 «Прямая в пространстве»	85
Лекция № 13 «Прямая на плоскости»	91
Лекция № 14 «Окружность, эллипс»	97
Лекция № 15 «Гипербола, парабола»	103
Лекция № 16 «Сфера, эллипсоиды»	111
Лекция № 17 «Параболоиды, цилиндры»	118
Предметный указатель	123
Греческий Алфавит	127

 

ЗАМЕТКИ

 

Александр Александрович Смирнов

 

 

                

ТЕОРИЯ МНОЖЕСТВ,