Сфера
Метод сечений
Эллипсоиды
5. Гиперболоид
Цели занятия: изучить понятие поверхностей второго порядка; на основе полученных знаний по теме «Кривые второго порядка»; изучить метод сечений и научиться строить поверхности второго порядка.
Роль и место лекции
В предыдущих лекциях были даны такие понятия аналитической геометрии, как кривые второго порядка, плоскость и прямая в пространстве. Понимание этих тем особенно важно для восприятия данной лекции. Она позволит сформировать математическое пространственное мышление. Для лучшего усвоения материала необходимо рассматривать пространственные объекты в сечениях или в разрезе. Когда сформируется представление о геометрическом объекте, необходимо представить его в целом.
Предложенный материал особенно важен для тех специальностей, где необходимо строить геометрические модели объектов. Например, в географии при моделировании планетарных поверхностей и их участков, моделировании объемных тел залежей ископаемых; в программировании при компьютерной анимации (понятие «полигон» непосредственно связано с геометрическими фигурами в пространстве); в астрономии при построении траекторий движения космических тел; в биологии в вопросах, связанных с необходимостью исследования функций многих переменных, например зависимости популяции от среднегодовой температуры и широты местности, а так же при построении эквипотенциальных поверхностей и линий уровня.
1. Общее выражение поверхности вращения
Вывод уравнения поверхности
Определение 1
Поверхности второго порядка – это такие поверхности, которые описываются алгебраическими уравнениями второго порядка.
Определение 2
Поверхность вращения – поверхность, образованная вращением плоской кривой вокруг координатной оси.
|
(рис. 1):
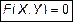, (1)
где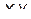 
– текущие координаты кривой L. Т. е. Z=0 Образуем поверхность вращением L вокруг оси Oy. Возьмем некоторую точку 
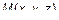на образованной поверхности 
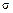. Проведем через эту точку плоскость 
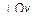. Обозначим 
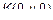– точка пересечения этой плоскости с осью Oy, а 
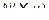– точка пересечения этой плоскости с кривой L. Ординаты трех точек равны, поскольку лежат в одной плоскости 
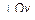, т. е. 
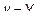. Очевидно 
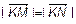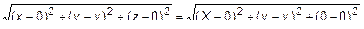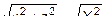или 
,
, или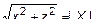 
откуда 
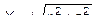. (2)
Подставим (2) в (1) получим уравнение
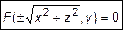(3)
с тремя переменными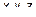 
, являющихся координатами точек поверхности, следовательно (3) есть уравнение поверхности вращения 
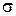. Сравнивая (1) и (3) можно определить правило образования поверхности вращения.
1.2. Правило образования поверхности вращения
Чтобы из уравнения кривой получить уравнение поверхности вращения надо в уравнении кривой оставить неизменной переменную, одноименную с осью вращения, а другую заменить корнем квадратным из суммы квадратов заменяемой переменной и недостающей в уравнении кривой.
ПРИМЕР 1.
Найти уравнение поверхности, образованной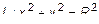 
. Будем вращать кривую вокруг оси Ox. Согласно правилу образованная поверхность будет описываться уравнением 
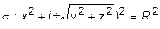или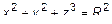 
. Это уравнение сферы с центром в начале координат, R – радиус.
|
Определение 1.
Сферой называется геометрическое место точек пространства, равноудаленных от одной точки – центра сферы.
Зададим центр сферы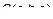 
, R – радиус. Тогда согласно определению 
определим выражение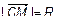 
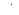
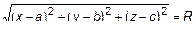или
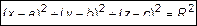. (4)
Это уравнение сферы в каноническом виде. Раскроем скобки. Тогда уравнение (3) запишем в виде общего
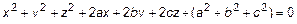
алгебраического уравнения второго порядка. Т. е. сфера принадлежит к уравнениям второго порядка. Чтобы от общего уравнения перейти к каноническому надо выделить полные квадраты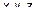 
.
Признаки, характеризующие уравнение сферы:
- коэффициенты при квадратах текущих координат равны;
- отсутствуют члены, содержащие произведения текущих координат.
ПРИМЕР 1.
Изобразить тело, ограниченное поверхностями: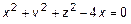 
, 
, 
.
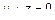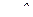Решение. В первом уравнении выделим полный квадрат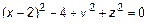 
или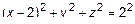 
. Это сфера в центром 
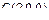. Уравнение 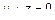– плоскость, проходящая через начала координат и ось 
. Тело отсекаемое этими поверхностями имеет вид (рис. 2).
3. Метод сечений
|
1. Находят уравнения линий пересечения поверхности с координатными плоскостями или плоскостями параллельными им. При этом необходимо решать систему уравнений.
2. Изображая каждую линию сечения, получают изображение поверхности.
3. Два одинаковых типа сечений дают название поверхности, а третье сечение, отличное от двух одинаковых, дает определение к названию. Например, если в сечениях две параболы и один эллипс, следовательно, поверхность эллиптический параболоид.
4. Эллипсоиды
Получим поверхность, вращая кривую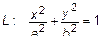 
– эллипс вокруг оси 
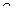. Согласно правилу, уравнение поверхности будет иметь вид
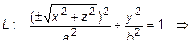
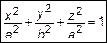. (5)
Для исследования этой поверхности применим метод сечений.
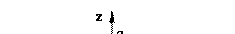1. Сечение плоскостью 
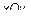, т. е. 
, тогда
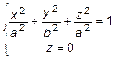или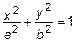 
– эллипс.
2. Сечение плоскостью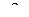 
, т. е. 
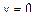, тогда
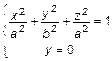или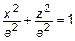 
– окружность.
|
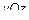, т. е. 
, тогда
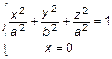или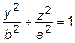 
– эллипс.
Два эллипса, одна окружность, следовательно, это эллипсоид вращения рис. 3. Если эллипсоид вращения деформирован сжатием или растяжением в области кругового сечения, то получается трехосный эллипсоид или эллиптический эллипсоид
.
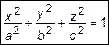4. Гиперболоиды
4.1. Однополостный гиперболоид
Получим поверхность, вращая кривую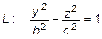 
– гиперболу вокруг оси 
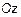. Согласно правилу уравнение поверхности будет иметь вид
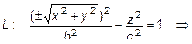
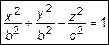. (6)
Для исследования этой поверхности применим метод сечений.
1. Сечение плоскостью 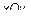, т. е. 
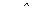, тогда
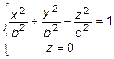или
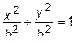– окружность.
2. Сечение плоскостью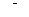 
, т. е. 
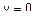, тогда
|
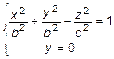или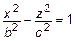 
– гипербола.
3. Сечение плоскостью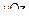 
, т. е. 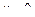, тогда
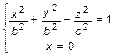или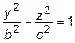 
– гипербола.
То есть это гиперболоид вращения рис. 4.
4.2. Двуполостный гиперболоид
Получим поверхность, вращая кривую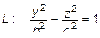 
– гиперболу вокруг оси 
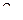. Уравнение поверхности будет иметь вид
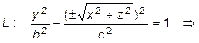
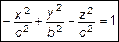. (7)
Для исследования этой поверхности применим метод сечений.
1. Сечение плоскостью 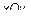, т. е. 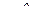, тогда
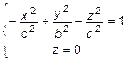или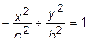 
– гипербола.
2. Сечение плоскостью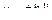 
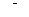, поскольку при 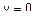решений нет (мнимая окружность), поэтому делаем сечение параллельной плоскостью, тогда
или 
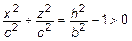– окружность. Отметим, что при
3. Сечение плоскостью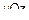 
, т. е. 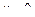, тогда
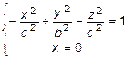или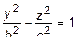 
– гипербола.
Следовательно, это гиперболоид вращения рис. 5.
|
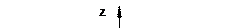
Если гиперболоид вращения деформирован сжатием или растяжением в области кругового сечения, то получается эллиптический гиперболоид
а) однополостный
;
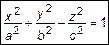б) двуполостный
.
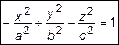Заключение
В лекции дан метод сечений, используемый при построении поверхностей второго порядка. Понимание предложенного материала важно для изучения следующей лекции, посвященной параболоидам, цилиндрическим и коническим поверхностям. Важно понять, что аналитическая геометрия в пространстве отличается от аналитической геометрии на плоскости только лишней размерностью. Очевидно, что при необходимости можно рассматривать геометрические законы и в n-мерном пространстве. С точки зрения теории множеств поверхность – это отображение элементов множества декартовой плоскости (или упорядоченных пар) в элементы множества действительных чисел.
Отметим наиболее важное:
- поверхности второго порядка описываются уравнениями второго порядка;
- поверхности вращения образуются вращением плоской кривой второго порядка вокруг координатной оси;
- из уравнения кривой можно получить уравнение поверхности;
- если вращение осуществлять не по круговой, а по эллиптической траектории, то можно получить эллиптические поверхности;
- метод сечений заключается в рассмотрении кривых, образуемых при сечении поверхности некоторыми плоскостями
Литература
1. Баврин И.И. Высшая математика. – М.: Просвещение, 1980.
2. Ефимов Н.В. Краткий курс аналитической геометрии. – М.: Физматлит, 2002.
Лекция 17
118
Поверхности второго порядка
Параболоиды
Цилиндрические поверхности
3. Конические поверхности
Цели занятия: научиться строить поверхности типа параболоидов; изучить конические и цилиндрические поверхности.
Роль и место лекции
В лекцией рассмотрены такие важные типы поверхностей, как цилиндрические и конические. Материал ограничивается случаями плоской направляющей и прямой образующей. Приведенные в этой лекции сведения, необходимы при изучении тем «Поверхности уровня» и «Дифференциал функций многих переменных и его приложения», и т. д. Обратите внимание на поверхности типа гиперболического параболоида.
1. Параболоиды
Дата: 2018-12-21, просмотров: 255.
