Понятие диагностической шкалы. В результатах педагогической диагностики тесно взаимосвязаны качественные и количественные характеристики. Качество — это совокупность свойств, указывающих на то, что представляет собой предмет, чем он является. Качеством называется также существенная определенность предмета, явления или процесса, в силу которой они являются данным предметом, явлением или процессом. Традиционно качество раскрывается с помощью описания признаков.
Количество определяет размеры и отождествляется с мерой, числом, измерением. При этом измеряется не сам объект, а его свойство или отличительный признак. В широком смысле измерение — это особая процедура, посредством которой числа (или порядковые величины) приписываются вещам по определенным правилам. Сами правила состоят в установлении соответствия между некоторыми свойствами чисел и некоторыми свойствами вещей. Возможность данного соответствия и обосновывает важность измерения в педагогике.
Анализируя качество, исследователь определяет, к какому классу уже известных явлений принадлежит данное качество и в чем его специфика. Затем устанавливает причинно-следственные зависимости между явлениями. Задача количественного анализа сводится к измерению и счету выявленных свойств. Переход от качественного изучения к количественному описанию осуществляется в следующей последовательности действий:
243
- 
регистрация — выявление определенного качества у явлении данного класса и подсчет количества его проявлений (например, количество выборов при социометрических методиках);
- ранжирование — расположение собранных данных в определенной последовательности (убывание или нарастание зафиксированных показателей), определение места в этом ряду изучаемых объектов (например, составление списка членов группы в порядке убывания их выборов);
- шкалирование — присвоение баллов или других цифровых
показателей исследуемым характеристикам.
Шкала (от лат. зса1а — лестница) представляет собой числовую систему, в которой отношения между различными свойствами объектов выражены свойствами числового ряда. Шкала — это способ упорядочивания объектов произвольной природы. Шкалирование как количественный метод исследования дает возможность ввести цифровые показатели в оценку отдельных сторон педагогических явлений.
Это требует глубокого проникновения в суть изучаемых (в том числе педагогических) явлений, логического осмысления проблемы. Например, чтобы измерить степень развития любого морального качества у школьников, следует установить, в чем конкретно оно проявляется. Затем эти конкретные проявления включаются в шкалу в виде непрерывного ряда от простого к сложному. Каждое из конкретных проявлений морального качества оценивается количественно.
Измерения можно проводить на четырех уровнях, каждому из которых соответствует своя шкала: 1) шкала наименований (или номинальная шкала), 2) шкала порядка (или ранговая, ординальная шкала); 3) интервальная шкала, 4) шкала отношений (пропорциональная шкала).
При этом каждый тип шкалы может быть охарактеризован соответствующими числовыми свойствами. Рассмотрим более подробно основные свойства разных типов шкал, эмпирические операции, допустимые для каждого типа шкал, а также статистические приемы обработки и анализа исходных, или, как их чаще называют, первичных, результатов исследования.
Номинальная шкала. Шкалу наименований иначе называют номинальной (назывной), потому что с ее помощью предметы лишь группируются по классам на основании наличия у них общего признака или свойства. С помощью шкалы каждой группе приписывается определенный числовой индекс.
Примером таких шкал является группировка людей по полу, социальному положению, месту жительства, семейному положению. Очевидно, что, присвоив, к примеру, девочкам индекс 0, а
244
мальчикам — 1, мы с уверенностью можем сказать лишь то, что эти группы различаются по данному признаку, если их индексы различны (или равны, если равны их индексы). Определить же, на сколько или во сколько раз они отличаются и даже какой показатель больше или меньше, номинальная шкала не позволяет. Цифровые индексы 0 и 1 взяты нами произвольно, вместо них вполне возможно обозначить группы другими цифрами в любом порядке, к примеру: 187 и 59. Эти числа — всего лишь имена. Потому шкала и называется номинальной (от лат. потеп — имя).
Мы выполнили бы номинальное измерение, если бы присвоили число 1 англичанам, 2 — немцам, а 3 — французам. Равна ли одному французу сумма одного англичанина и одного немца (1 + 2 = 3)? Конечно, нет. Если процесс присвоения чисел предметам представлял собой номинальное измерение, то действия с величиной, порядком и прочими свойствами чисел не будут иметь никакого смысла по отношению к самим предметам, поскольку мы не интересовались величиной, порядком и другими свойствами чисел, когда присваивали их (В. Г. Максимов).
При построении шкал наименований главными являются качественные различия, а количественные не принимаются во внимание. Поэтому числа, используемые для обозначения классов эквивалентности в этих шкалах, не отражают количественных различий выраженности изучаемого признака.
Назначение номинальной шкалы состоит в различении объектов по наличию или отсутствию признака, и применяется она для классификации объектов.
Порядковая (или ранговая) шкала измерений. Порядковая шкала (ординальная, ранговая) — это упорядоченная номинальная шкала, которая устанавливает не только равенство между объектами по выбранным признакам, но и отношения порядка. Она позволяет обнаружить в предметах различия в степени выраженности признака или свойства.
Общий вид порядковой шкалы:
а) максимально положительный ответ;
б) положительный ответ;
в) отрицательный ответ;
г) максимально отрицательный ответ.
При помощи порядковой шкалы изучаются отношения опрашиваемого к различным объектам, измеряется степень оценки им каких-то предметов и явлений, интенсивность проявления некоторых личностных характеристик, педагогических явлений.
Если ответам на приведенной выше ранговой шкале присвоены номера 4, 3, 2, 1, то столь же правомерно и присвоить номера
245
254, 52, 37, 0 — важно лишь, что эти четыре числа идут в порядке убывания. Порядковая шкала не дает возможности изменить расстояние между объектами, проецируемыми на нее, она характеризует только порядок расположения объектов по возрастанию или убыванию их свойств. Данный вид измерения использует два свойства чисел — различие их и порядок расположения. Шкала порядка неравномерна. Расстояния между соседними метками шкалы неизвестны. Следовательно, некорректно складывать, вычитать, умножать, делить порядковые места или с их помощью вычислять среднее арифметическое значение.
То, что Саша в классе первый по росту, а Денис — третий, означает лишь то, что Саша самый высокий и между ним и Денисом есть еще кто-то один. Но знание ранга не дает возможности ответить на такие вопросы, как «на сколько?» или «во сколько раз?». Зато можно с уверенностью сказать, что если Сергей выше Артема, а Михаил ниже Артема, то Сергей выше Михаила.
Школьные отметки также представляют собой ранговую шкалу, которая позволяет утверждать, что ответ на «5» лучше, чем на «3». Здесь отсутствует равномерность распределения между выставляемыми отметками. Никто не может утверждать, будто различие между отметками «1» и «2» столь же велико, как между «3» и «4» или «4» и «5». Именно поэтому неправомерно выставлять в качестве итоговой оценки среднюю арифметическую.
Порядковая шкала позволяет различать уровень проявления свойств объекта, но не определяет величину различия проявления свойств, поскольку не имеет эталона (масштабной единицы). Ее применение целесообразно в целях упорядочения совокупности объектов по интенсивности проявления диагностируемого свойства.
Большая часть шкал, широко применяемых в педагогических, социологических, социально-психологических исследованиях, — это шкалы порядка.
Интервальная шкала. Такое присвоение объектам чисел, при котором равные разности чисел соответствуют равным разностям значений измеряемого признака или свойства объектов, становится возможным при использовании интервальной шкалы. Она образуется на основе порядковой шкалы путем присвоения числовых эквивалентов ее делениям. Интервальная шкала характеризуется тем, что интервалы между объектами могут быть измерены, а значит, появляется возможность определять не только признаки свойств предметов, но и количественное различие степеней свойств этих предметов.
Шкала интервалов имеет отличительные свойства, заключающиеся в следующих возможностях: определение признаков, свойств предметов, выявление различия в степени измеряемых свойств,
246
опора на условно определенную нулевую точку отсчета, произвольное определение величины единицы измерения (интервальной величины).
Для интервального измерения устанавливается единица измерения (градус, метр, сантиметр, грамм и т.д.). Предмету присваивается число, равное количеству единиц измерения, которое приблизительно соответствует количеству измеряемого свойства. Например, температура металлического бруска равна 86 °С.
При создании шкал интервалов основная проблема состоит в том, чтобы изобрести такие операции, которые позволили бы уравнять единицы шкал. В шкале имеются интервалы с соответствующими номерами, и характер ответов испытуемого фиксируется на определенной точке шкалы, выражающей его отношение к данному вопросу.
Для получения интервальной шкалы используют вопросы с оценкой: закрытые вопросы, к которым прилагается оценочная характеристика типа «полностью одобряю», «отношусь нейтрально», «он вызывает во мне некоторое неодобрение», «...полное неодобрение», «не знаю». В этом случае исследователь получает не только тот ответ, с которым респондент согласен, но и тот, с которым он не согласен, а также видит меру этого согласия и несогласия. В результате появляется возможность провести количественную обработку ответов, дав каждому ответу определенную количественную оценку.
Для построения трехградусной односторонней шкалы на вопрос «Доволен ли ты своей школой?» предлагается три ответа: очень — 10; не очень — 5; не доволен — 0.
Многоградусная односторонняя шкала имеет такой вид: очень доволен — 6; относительно доволен — 4; не очень доволен — 2; совсем не доволен — 0.
Шкалы могут быть и двусторонние, т.е. иметь оценку ответов со знаком «минус». Например, на вопрос «Окончив школу, как ты будешь о ней вспоминать?» даются следующие ответы: очень хорошо «+10»; довольно хорошо «+5»; нейтрально «0»; довольно плохо «-5»; очень плохо «-10».
Шкалам интервалов присущи все те отношения, которые характерны для номинальных и порядковых шкал. Кроме того, для них возможно использование операций установления равенства, разности, сопоставления «больше — меньше» в отношении измеряемых свойств, а также утверждение равенства интервалов и равенства разностей между значениями одной шкалы. Однако операции сложения, умножения и деления с этими данными сомнительны. Между показаниями на интервальной шкале нельзя установить пропорций (соотношения). К примеру, предмет, имеющий температуру 30°, не будет втрое теплее того, у которого температура 10°.
247
Эти рассуждения обусловлены тем, что три момента на шкале интервалов устанавливаются произвольно: нуль шкалы (точка отсчета, которая не означает полного отсутствия измеряемого признака), величина единицы измерения и направление, в котором ведется подсчет.
Шкала интервалов имеет масштабную единицу, благодаря чему позволяет определять различие, степень проявленности и величину различия измеряемого свойства объекта. Она не определяет уровня исчезновения свойства и пропорций. Эту шкалу целесообразно применять в тестовых методиках.
Шкала отношений. Когда нулевая точка на интервальной шкале не произвольна, а указывает на полное отсутствие измеряемого свойства, эта шкала становится шкалой отношений, или пропорциональной шкалой. Второе название указывает на то, что числа, приравниваемые к классам объектов, пропорциональны степени выраженности измеряемого свойства. В условиях шкалы отношений возможны утверждения, что у А в 2 (5, 7,5) раза больше свойств, чем у В. Измеритель может заметить отсутствие свойства и имеет единицу измерения, позволяющую регистрировать различающиеся значения признака.
Шкала отношений характеризуется возможностью определения каждого из следующих четырех соотношений: равенство, ранговый порядок, равенство интервалов и равенство отношений. Все операции с цифрами (сложение, вычитание, умножение и деление) можно производить без каких-либо ограничений. Примерами измерения в шкале отношений могут служить измерение размеров и массы предметов, измерение температуры по шкале Кельвина. Числа, присвоенные объектам, обладают всеми свойствами объектов интервальной шкалы, но помимо этого на шкале существует абсолютный нуль.
Шкала отношений определяет абсолютно любые отношения между уровнями проявления свойств, имеет масштабную единицу, фиксирует исчезновение свойства.
В психолого-педагогической диагностике она используется крайне редко, например для измерения скорости выполнения задания, количества сделанных однородных ошибок, количества запоминаемых при первоначальном изучении слов иностранного языка и т.д.
Специфика использования разных типов шкал. Разработка шкалы для измерения требует учета таких условий, как соответствие измеряемых объектов, явлений измерительному эталону; выявление возможности измерения интервала между различными про-
248
явлениями измеряемого свойства; определение конкретных показателей различных проявлений измеряемых явлений.
Различие уровней измерения качества можно проиллюстрировать простым примером:
- если в диагностике используется критерий факта , т.е. выявляется наличие или отсутствие какого-либо свойства, то получается номинальная шкала (к подобным свойствам, например, относится пол испытуемого);
- если можно установить и степень выраженности этого свойства («больше» — «меньше»), то строится ранговая шкала (примером таких свойств является степень произвольности внимания);
- если фиксируется, насколько диагностируемое свойство у одних испытуемых выражено больше, чем у других, то можно получить интервальную шкалу (большинство тестов успеваемости, например, дают такую возможность);
- если же выясняется, во сколько раз больше свойство выражено у одних испытуемых чем у других, то получим пропорциональную шкалу (например, антропометрические параметры: рост, масса, объем легких и т.д.).
Шкалы наименований самые «слабые». Числа в них используются только для обозначения принадлежности исследуемого объекта к определенному классу. В ранговых шкалах устанавливается порядок следования, отношения «больше» и «меньше», общая иерархия. Интервальная шкала дополнительно предусматривает определенные расстояния между отдельными (двумя любыми) числами на шкале, а в шкале отношений, кроме того, определена еще и нулевая точка (точка отсчета). Однако по мере возрастания точности и функциональности шкал возрастает и трудность в их разработке, усложняются соответствующие диагностические методики. Поэтому в соответствии с решаемыми конкретными задачами каждый раз следует выбирать минимально достаточную шкалу.
Выделение уровней развития исследуемого свойства — одна из типичных проблем при выборе оптимальной шкалы. При целостном подходе к изучению педагогических явлений и процессов развитие понимается как переход качества от низших уровней к высшим. При выделении уровней чаще всего берут за основу структурно-функциональный признак: измеряемое качество (например, отношение) при переходе на другой уровень меняет свою структуру и функции.
Применяя категорию целостности, можно рассматривать каждый новый уровень развития как качественно определенное состояние целого. Считается, что переход качества на более высокий уровень означает не исчезновение интегративных свойств предшествующего уровня, а преобразование их в более совершенные. Некоторые ученые отмечают, что путь развития есть систем-
249
но-целостный процесс и включает следующие четыре уровня системности.
Первый уровень — аморфность системы, разрозненность ее элементов, отсутствие устойчивых связей между ними, когда нет еще возможности говорить о сколько-нибудь сложившейся структуре. Система ведет себя непредсказуемо, велика ее зависимость от условий внешней среды.
Второй уровень — появление связей между группами элементов в системе, в ней образуются «фрагменты структуры», устанавливаются причинно-следственные связи, поведение системы становится предсказуемым в определенных ситуациях, но остается неустойчивым.
Третий уровень — наличие связей практически между всеми элементами системы, выстраивание ее внутренней структуры, более устойчивое поведение системы, т. е. оно проявляется на уровне тенденций в большинстве ситуаций жизнедеятельности. Это уровень связного целого, однако система еще неустойчива, ее структура с большой степенью вероятности может быть разрушена внешними воздействиями.
Четвертый уровень — оптимально связное целое, связи между элементами системы устойчивы, выстраиваются в иерархическую структуру; устойчивым и автономным (относительно независимым от внешней среды) становится и поведение системы. Это стадия саморазвития системы, когда усиливаются внутренние факторы ее развития, а внешние отступают на второй план, когда система включает освоенную среду в качестве элементов своей структуры.
Выделенные уровни могут стать основой для построения ранговой шкалы, которую при соответствующей статистической обработке можно перевести в интервальную.
9.2. Математическая и статистическая обработка данных1
Использование статистики в исследовании. Там, где это возможно, качественный анализ результатов диагностики стремятся дополнить количественным — математической обработкой и статистическим анализом. Методы статистики позволяют не только установить причинно-следственную связь, но и прогнозировать протекание процессов на основе статистических моделей. Имеются три главных раздела статистики.
• Описательная статистика позволяет описывать, подытоживать и воспроизводить в виде таблиц или графиков данные того
В разделе использованы материалы и разработки М.И.Еременко.
250
или иного распределения, вычислять среднее для данного распределения, его размах и дисперсию.
• Индуктивная статистика необходима тогда, когда требуется проверить, можно ли распространить результаты, полученные на данной выборке, на всю популяцию, из которой выборка взята. Иначе говоря, она позволяет установить, до какой степени можно путем индукции распространить на большее число объектов ту или иную закономерность, обнаруженную при изучении ограниченной группы в ходе какого-либо наблюдения или эксперимента. Следовательно, индуктивная статистика необходима после получения эмпирических данных, на этапе обобщения и конструирования выводов.
• Корреляция показывает вероятностную или статистическую зависимость. В отличие от функциональной зависимости корреляция возникает тогда, когда зависимость одного из признаков от другого осложняется наличием ряда случайных факторов.
Выбор методов обработки данных, полученных в результате диагностики, во многом определяется тем, какой шкалой (номинальной, ранговой, интервальной или шкалой отношений) пользовались при измерениях; подчиняются ли полученные данные закону нормального распределения; являются ли сравниваемые выборки зависимыми или независимыми.
Соответственно ответом на эти вопросы при анализе и математической обработке массового материала применяются статистические методы, в число которых входят вычисление средних величин, а также подсчет степеней рассеивания около этих величин — дисперсии, среднего квадратичного отклонения, коэффициента вариации и др.
Основные этапы обработки результатов. Полученные в результате диагностики данные — это основные элементы, подлежащие анализу. Данными могут быть количественные результаты, другая информация, которую можно классифицировать или разбить на категории с целью обработки.
Применение в педагогическом исследовании статистических методов включает в себя следующие этапы.
Сбор эмпирических данных методами наблюдения, тестирования, эксперимента, анкетирования и других в целях получения количественных сведений о каких-либо явлениях, заполнение математической модели конкретными цифрами.
Сводка полученных сведений, нахождение обобщающих числовых данных и их обработка в пределах формальной математической модели.
Составление математической модели для последующего описания с помощью цифр существенных свойств изучаемого объекта.
Анализ и интерпретация данных, конструирование содержательных педагогических выводов.
9^1
Статистическая обработка цифровых данных начинается с группировки. Для этого прежде всего необходимо расположить данные каждой выборки в возрастающем порядке. Многие данные принимают одни и те же значения, причем одни из них встречаются чаще, другие — реже. Графически распределение можно представить в виде столбиковых диаграмм. При этом распределение данных по их значениям дает больше информации, чем простое представление в виде рядов. Подобную группировку используют в основном для качественных данных, четко разделяющихся на обособленные категории.
Количественные данные отличаются от качественных своей многочисленностью и располагаются на непрерывной шкале. Поэтому такие данные предпочитают группировать по классам, чтобы яснее была видна основная тенденция распределения. Группировка по классам заключается в объединении данных с одинаковыми или близкими значениями в классы и определении частот для каждого класса. Способ разделения на классы и частота каждого класса зависят от того, что именно экспериментатор хочет выявить при разделении измерительной шкалы на равные интервалы.
Распределение данных. Многочисленные методы статистической и математической обработки данных, относящихся к интервальной шкале, исходят из гипотезы, что их значения подчиняются нормальному распределению, при котором большая* часть значений группируется около некоторого среднего значения, по обе стороны от которого частота наблюдений равномерно снижается.
|
|
| 252 |
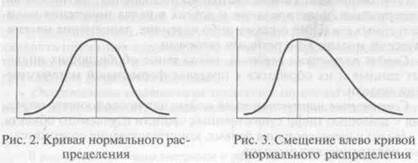
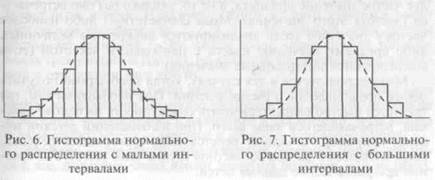
Если построить график такого распределения, когда горизонтальная ось показывает значение признака, а вертикальная — количество соответствующих результатов, то получится симметричная кривая, похожая на колокол (рис. 2). В тех случаях, когда какие-либо причины препятствуют более частому появлению значений, которые выше или ниже среднего, образуются асимметричные распределения (рис. 3, 4). Чем больше значений признака находится вблизи среднего, тем острее вершина кривой; при раз-
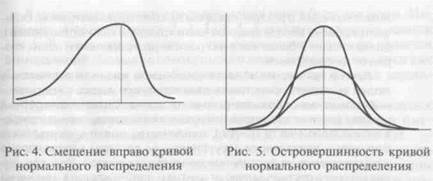
бросе результатов (когда многие из них существенно отличаются от среднего) кривая становится более пологой (рис. 5).
Распределение может быть представлено и гистограммой, т.е. последовательностью столбцов, каждый из которых опирается на один разрядный интервал, а высота его отражает число случаев, или частоту, в этом разряде. На рис. 6 и 7 приведены примеры гистограмм распределения данных с разными значениями интервалов. Применение гистограмм удобно при оценках распределения непрерывной величины (например, распределение учащихся по уровням доходов на одного члена семьи). Если визуальное сравнение реальной гистограммы с кривой нормального распределения кажется недостаточным, можно использовать разработанные в математической статистике таблицы и формулы оценки нормальности распределения, а также методы приведения распределения к нормальному виду.
|
|
| 253 |
Кривую нормального распределения называют также «колоколом Гаусса» или Гауссовой кривой, по имени впервые описавшего ее немецкого математика К. Ф. Гаусса. Эта математическая модель показывает, каким образом значения величин, называемых случайными переменными, распределяются относительно среднего значения. Одна из таких случайных переменных — рост человека. Ко-
личество людей с ростом, средним для исследуемой группы, сконцентрировано вблизи средней части кривой, а количество людей с более низким и более высоким ростом распределено с обеих сторон от центра кривой.
Другой пример из области социальной жизни — стремление людей выглядеть представителями «среднего класса». «Нормальный» доход имеют большинство из тех, с кем общается конкретный человек (количество людей, имеющих такой доход, сконцентрировано в средней части кривой), а количество людей с чрезвычайно большим и практически отсутствующим доходом распределено соответственно на противоположных концах кривой. Человек, доход которого отстоит далеко от центра и приближается к одному из концов кривой нормального распределения, естественно, хочет иметь более «нормальный» имидж. Легко понять желание малоимущего выглядеть «поприличнее»; также естественным кажется желание богатого человека в повседневном общении выглядеть «попроще». Однако странным (эпатажным) выглядит желание кого-либо, находящегося на одном конце кривой нормального распределения, передвинуться еще дальше.
Реальное распределение частот измеряемых величин может иметь не одну, а несколько вершин. В этом случае предпочтительно рассматривать интервальные распределения, когда в каждом из интервалов имеется одна вершина.
Меры центральной тенденции. В зависимости от характера данных (по какой шкале они были получены: номинальной, ранговой или интервальной) для количественной характеристики совокупностей используют средние показатели: моду, медиану или среднее арифметическое.
Мода — наиболее просто получаемая мера центральной тенденции. Это такое значение во множестве наблюдений, которое встречается особенно часто. Например, в совокупности значений (2; 8; 8; 3; 5; 3; 10; 5; 5; 5) модой является 5, потому что это значение встречается чаще любого другого.
Необходимо подчеркнуть, что мода представляет собой наиболее частое значение признака, а не то, сколько раз оно встречается (частота этого значения). Мода соответствует либо наиболее частому значению (если анализируются дискретные величины), либо среднему значению класса с наибольшей частотой (если анализируются интервальные значения).
Мода используется в тех случаях, когда необходимо получить общее представление о распределении. Она необходима там, где требуется быстро охарактеризовать совокупность на основе явления, встречающегося чаще всего. При изготовлении детской мебели, например, за основу берется мода (рост, масса ребенка, встречающиеся в данной возрастной группе чаще всего), а не средние арифметические данные детей.
254
В некоторых случаях у распределения могут быть две моды. Например, в совокупности 2, 3, 3, 4, 5, 5 модами являются оценки 3 и 5. В этом случае говорят, что совокупность оценок является бимодальной. Большие совокупности оценок рассматриваются как бимодальные, если они образуют полигон частот с двумя вершинами даже тогда, когда частоты не строго равны.
Принято считать, что в том случае, если все значения оценок встречаются одинаково часто, совокупность данных моды не имеет. Например, в совокупности 2, 2, 3, 3, 4, 4, 5, 5 моды нет.
Моду как меру центральной тенденции интерпретируют следующим образом: она имеет такое значение, которое наилучшим образом заменяет все значения; когда модой заменяют любое значение ряда чисел, мы имеем наибольшую частоту совпадений с числами ряда.
При использовании номинальных шкал можно определить, какой номинальный класс имеет самый большой состав, и назвать этот класс модой распределения. В данном случае мода является статистической мерой центральной тенденции: если продолжить наблюдения, изменяя условия, в которых они проводились ранее, то мода будет представлять наблюдения, которые можно ожидать с максимальной вероятностью.
Предположим, что в классе 14 детей являются единственными детьми в семье (эту категорию условно обозначим нулем — 0); 11 детей имеют брата или сестру (обозначим единицей — 1); 5 детей — двух братьев или сестер (присвоим данной категории детей цифру 2); 3 ребенка — трех (обозначим цифрой 3) и 1 ребенок — четырех братьев и сестер (обозначим цифрой 4). Следовательно, показатель 0 («единственный ребенок в семье») является здесь модальной величиной. В данном примере упорядочить по возрастающей номинальные величины условно можно следующим образом: 0,0, 0,0, 0, 0,0,0,0,0, 0, 0,0,0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,2, 2, 2, 2, 2,3,3,3,4.
Следует заметить, что для малых групп часто о такой замене не может быть и речи. Например, группа из пяти учащихся имеет следующую успеваемость: 2, 2, 2, 5, 5. Модальный актив группы составляет величину 2. Эта цифра точно характеризует успеваемость трех учащихся группы, но является чрезвычайно некорректной в отношении двух других.
Мода для больших групп данных — достаточно стабильная мера центра распределения. Во многих распределениях значительного числа измерений, используемых в педагогике и психологии, мода близка к двум другим мерам — медиане и среднему арифметическому.
Медиана — это число, обозначающее середину множества чисел, т.е. половина чисел имеют значения большие, чем медиана,
255
а половина чисел — меньшие, чем медиана. При нечетном числе членов ранжированного ряда медиана соответствует центральной величине ряда.
Например, мы имеем следующий ранжированный ряд: 4, 5, 7, 9, 11, 13, 15, 17, 18. В середине данного ряда находится число 11, следовательно, оно и является медианой. Число, которое является серединой множества чисел, совсем не обязательно должно находиться посередине числового массива данных, например медиана числового ряда:1, 2, 8, 15, 7, 5, 9 — равняется 7, потому что для ее нахождения нужно первоначально упорядочить множество по возрастанию входящих в него значений (1, 2, 5, 7, 8, 9, 15) или по их убыванию (15, 9, 8, 7, 5, 2, 1).
Если рассмотреть совокупность отметок (2, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5), то аналогично можно обнаружить, что ее медиана равна 4. Однако для больших совокупностей данных, где есть объединенные классы (по нескольку одинаковых значений), медиану проще находить с использованием табличной записи. Пусть мы имеем 16 отметок.
| Оценка | Частота | Накопленная частота |
| 2 | 1 | 1 |
| 3 | 3 | 4 |
| 4 | 8 | 12 |
| 5 | 4 | 16 |
Примечание. Частота показывает, сколько раз встречается это значение в совокупности. Накопленная частота, как это видно из таблицы, равна сумме частот данной отметки и всех предыдущих. Таким образом, накопленная частота самой высокой отметки равна общему количеству отметок.
Медиана выбирается 8-й и 9-й оценками в приведенной выше таблице, поскольку всего отметок 16. По таблице видно, что она располагается в интервале «четверок». Поскольку в верхней границе ряда оценок накоплено 4 оценки (I +3 = 4), мы должны еще накопить 8-4 = 4 частоты, а всего в интервале 8 «четверок». Поэтому медиана делит интервал «четверок» пополам. В интервале между значениями 3,5 и 4,5 лежит 8 «четверок». Следовательно, медиана равна 3,5 + 4: 8 = 4.
Интерпретируем значение медианы на следующем примере. Пусть мы получили следующий ряд отметок: 2, 2, 3, 4, 5, 5, 5, где медиана равна оценке 4 (поскольку именно 4 — расположена посередине упорядоченной сокупности отметок). Разность между 4 и 2 составляет два, между 4 и 5 — минус один. Сумма этих разностей, взятых по абсолютному значению (т.е. без знака), равна
256
2 + 2+1 + 1 + 1 + 1=8и всегда меньше суммы разностей относительно любого другого числа данного ряда. В самом деле, разности между 5 и другими числами соответственно равны: 3, 3, 2, 1, О, О, а сумма абсолютных разностей всех значений относительно медианы всегда меньше суммы разностей относительно любой другой точки. Из этого следует, что если вместо каждой оценки ряда выбрать медиану, то будет допущена минимальная суммарная ошибка.
Медиана — один из членов ряда распределения или, как это бывает в четных рядах, очень близкая к нему величина. Опираясь на значение медианы, можно охарактеризовать структуру ряда: имеются ли равномерное распределение вокруг среднего, накопление величин по возрастающим или убывающим интервалам?
Среднее арифметическое совокупности значений определяется суммированием всех данных и последующим делением на их количество. Среднее арифметическое дает возможность охарактеризовать исследуемую совокупность одним числом; сравнить отдельные величины со средним арифметическим; определить тенденцию развития какого-либо явления; сравнить разные совокупности; вычислить другие статистические показатели, так как многие статистические вычисления опираются на средние арифметические.
В качестве меры центральной тенденции при анализе данных используют понятие среднего, которое может быть не связано с каким-то цифровым показателем, а представляет обобщенную категорию мышления, например: «средний ученик», «средний учитель», «средняя успеваемость». Но среднее может быть и в цифровой форме, когда отражаются те или иные средние величины совокупности, вычисляются средние величины объема. Они характеризуются тем, что их числовое значение изменяется при изменении значения любого члена совокупности.
Кроме арифметического среднего в педагогическом исследовании применяют гармоническое, квадратическое и хронологическое среднее. Для вычисления различных средних и статистического анализа количественных данных в среде \\тпао\У8 можно использовать табличный процессор Ехсе1.
Выбор меры центральной тенденции. Решая вопрос о предпочтении определенной меры центральной тенденции, следует помнить, что при нормальном распределении все три основных показателя центральной тенденции близки по значению, а при асимметричном распределении — различаются. При этом каждая мера центральной тенденции обладает своими характеристиками, которые особенно значимы в определенных условиях.
В малых совокупностях чисел мода, как правило, нестабильна.
257
Например, для совокупности 2, 2, 2,3,4,4 мода равна 2, но если одну из оценок 2 заменить оценкой 4, то мода будет равна 4.
Медиана более стабильна, на нее не влияют «большие» и «малые» оценки. Например, для больших совокупностей оценок медиана останется прежней, если число минимальных или максимальных оценок резко изменится.
Например, совокупности 2, 2, 2, 3, 3, 3, 3,4,4,4, 5, 5, 5, 5 и 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 5 имеют одинаковые медианы.
На величину среднего влияет изменение каждого значения оценки. Особенно влияют результаты, которые можно назвать «выбросами», т.е. данные, находящиеся далеко от центра группы оценок. Преимущество это или нет — зависит от конкретных вопросов, которые решаются при анализе результатов диагностики. Для многих числовых совокупностей педагогических измерений мода и медиана — более стабильные показатели.
Например, дано множество значений: 1; 3; 3; 5; 6; 7; 8. Найдем среднее, медиану и моду: среднее равно 4,7; медиана равна 5; мода равна 3. Теперь удвоим максимальное значение во множестве значений: 1; 3; 3; 5; 6; 7; 16, в результате получим: среднее равно 5,9; медиана равна 5; мода равна 3.
Некоторые совокупности результатов педагогических измерений просто не имеют центральной тенденции. Это наблюдается для многомодальных совокупностей оценок (имеющих две и более моды).
Например, для совокупностей оценок: 2, 2, 2, 2, 2, 4, 4, 4, 4, 4 — среднее равно 3, несмотря на то что в этом ряду нет такой оценки. Ни среднее, ни медиана не в состоянии дать правильного представления об успеваемости этой группы. Более правильное представление в данном случае дает словесное описание: «50 % в группе имеют оценки "2", а остальные — "4"». Последнее на языке статистики может быть выражено так: гистограмма бимодальна, т. е. имеет две моды, одна равна 2, другая — 4.
Центральная тенденция групп данных, содержащих крайние значения, наилучшим образом измеряется медианой.
Например, у 99 учащихся показатель социальной адаптации изменяется от 44 до 85 (среднее значение — 64,5), а показатель одного учащегося равен 156. Средний показатель для 100 учащихся в этом случае будет 95. Это число не позволяет судить обо всей группе. В этом примере в качестве меры центральной симметрии следовало бы избрать медиану.
258
Медиану применяют в том случае, когда хотят определить точную середину ряда. Некоторые интервалы особенно большой частоты могут в значительной мере повлиять на среднее арифметическое. Преимущество медианы в том, что на нее такие чрезвычайные интервалы не влияют. Центральная тенденция совокупности данных с большими крайними выбросами наилучшим образом характеризуется медианой, когда распределение результатов унимодально.
Средние показатели не всегда подводят к верным выводам, источником достоверной научной информации они становятся лишь тогда, когда при их вычислении учитывается закон больших чисел, сущность которого заключается в следующем:
- закономерности совокупностей равномерного состава можно вычислить только при наличии достаточно большого количества данных;
- точность измерения закономерностей возрастает с увеличением количества элементов объекта исследования;
- отклонения отдельных явлений от среднего в ту или другую сторону, обусловленные несущественными, случайными обстоятельствами, при большом количестве элементов взаимно компенсируются;
- эти закономерности можно количественно выразить только в виде средних показателей.
Необходимо иметь в виду, что результаты вычисления средних значений можно использовать лишь при нормальном распределении данных, полученных при измерениях по шкале отношений или равномерной интервальной шкале.
Из сказанного становятся очевидными те ограничения, которые накладываются на использование статистических приемов обработки результатов, полученных на уровне шкалы наименований (номинальной шкалы). Поскольку операции арифметического характера не допускаются, то в качестве меры центральной тенденции можно использовать лишь моду. Модальный класс объектов определяют после подсчета абсолютных или относительных частот, т. е. встречаемости того или иного результата в каждом классе.
В порядковых (ранговых) измерениях значения чисел, присваиваемых предметам, отражают количество свойства, принадлежащего предметам. При обработке приписанных баллов используется медиана.
Совокупность характеризуется посредством среднего арифметического в том случае, если распределение параметров расположено симметрично по отношению к середине. При асимметричном или многовершинном распределении среднее арифметическое не подходит для описания совокупности. В таких случаях для характеристики совокупности лучше пользоваться модой.
?^ д
Меры связи. Исследователей часто интересует, как связаны между собой две переменные в различных массивах диагностических данных (успеваемость, учебные умения, учебная деятельность, самообразование и т.д.). Например: имеют ли ученики, научившиеся читать раньше других, тенденцию к более высокой успеваемости в последующие годы обучения? Наблюдаются ли в больших классах меньшие успехи в приобретении знаний, чем в небольших? Связана ли средняя продолжительность работы педагога в школе непосредственно со средней заработной платой? Для ответов на такие вопросы мы должны провести наблюдения по каждой переменной для группы объектов.
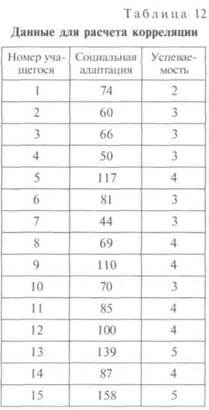
В табл. 12 приведены данные, собранные для ответов на вопросы: связаны ли показатель успеваемости по учебным предметам и социальная адаптация? Как выявить наличие связи между этими двумя характеристиками?
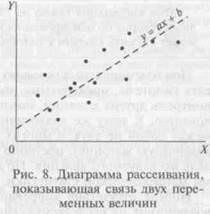
Для выявления связи двух переменных можно использовать анализ диаграммы рассеивания. Для этого на плоскости ХО К по горизонтальной оси X откладываются значения одной величины (в
нашем примере это показатель
|
|
социальной адаптации), по вертикальной оси У — другой величины (в нашем примере — успеваемость). Каждый ученик изображается точкой, одна координата которой равна показателю социальной адаптации, другая — успеваемости. Если получившаяся совокупность точек близка к графику линейной зависимости у - ах + Ъ (примерно так, как показано на рис. 8), то можно утверждать, что между двумя величинами существует значимая положительная связь (говорят, что эти величины имеют значимую корреляцию).
Связь двух величин можно выразить с помощью коэффици ента корреляции Пирсона. Иначе его еще называют коэффициентом регрессии. Он представляет собой безразмерный индекс в интервале от -1,0 до 1,0 включительно, который отражает степень линейной зависимости между двумя множествами данных.
260
|
|
В математической статистике выводятся соответствующие формулы для его вычисления. Однако с помощью компьютера можно вычислить коэффициент корреляции Пирсона в табличном процессоре Ехсе1, программном пакете 8ТАТ18Т1СА или других программах, не зная формул. Нужно только знать, как оценивать полученные числовые данные. Для этого можно использовать табл. 13.
При коэффициенте от +0,5 до 1 и -1 до -0,5 говорят о значимой связи, величина коэффициента от 0,00 до ±0,50 показывает незначимую связь величин.
В приведенном выше примере (см. табл. 12) анализ полученных данных показал, что обнаруживается значимая положительная корреляция, равная 0,81. Такую корреляцию называют значимой прямой связью. Но применение корреляции как единственного метода анализа причинности рискованно и может ввести в заблуждение.
Во-первых, даже в тех случаях, когда можно предположить существование причинной связи между двумя переменными, которые коррелированы, и коэффициент корреляции больше 0,50, еще нельзя говорить о том, что одна является причиной, а другая — следствием, например, что высокий уровень успеваемости по учебным предметам вызывает актив-
|
|
ную социальную адаптацию.
Во-вторых, часто наблюдаемая связь существует благодаря и другим переменным, а не только двум рассматриваемым.
В-третьих, взаимосвязи массивов переменных в психологии и педагогике слишком сложны, чтобы объяснением их мог служить лишь один числовой показатель. Успеваемость в школе — результат многочисленных влияний, да и сама по себе она — сложное явление, которое нельзя описать адекватно при помощи какого бы то ни было одного измерения.
261
Хотя корреляция прямо не указывает на причинную связь (она лишь говорит об одновременности наступления двух событий), она может служить ключом к разгадке причин.
При благоприятных условиях на ее основе можно сформулировать гипотезы, проверяемые экспериментально, когда возможен контроль других влияний, помимо тех, которые подлежат исследованию. К тому же аналогично можно вычислить корреляцию между собой не двух, а многих величин (так называемую корреляционную матрицу), построив на ее основе статистическую модель исследуемого явления. Но для этого нужно овладеть методами математической статистики.
Иногда отсутствие корреляции может иметь более глубокое воздействие на исследуемую гипотезу причинной связи, чем наличие сильной корреляции. Нулевая или близкая к нулю корреляция двух переменных может свидетельствовать о том, что никакого влияния одной переменной на другую не существует.
Репрезентативность выборки. Можно ли на основе диагностики, например, части учащихся класса делать выводы обо всем классе или о школе в целом? Такой вопрос обращает исследователя к оценке репрезентативности выборки.
Репрезентативность (от франц. гергезепШН/— показательный) в статистике — соответствие характеристик, полученных в результате выборочного наблюдения, показателям, характеризующим всю генеральную совокупность. Расхождение между указанными показателями представляет собой ошибку репрезентативности, которая может быть случайной или систематической.
Основная проблема репрезентативности выборки — величина и верность образцов.
Величина представленности образцов зависит от степени однородности целого (чем однороднее целое, тем меньше требуется образцов); от численности категорий и классов, на которые подразделяются результаты исследования (чем их больше, тем больше должно быть образцов); от количества работников, привлеченных к исследованию.
Выборки называются статистически однородными, если их распределения сходны, а различия между ними пренебрежимо малы. В противном случае, когда различия велики, а сходство пренебрежимо мало, выборки статистически неоднородны.
Размер выборки находится в зависимости от размера генеральной совокупности, подлежащей изучению, а также от цели исследования. Когда цель исследования заключается в изучении состо-
262
яния знаний ограниченного количества учащихся, например одного класса, объем выборки не может превысить численность этого класса. В отдельных случаях объем выборки может быть меньше численности учащихся класса из-за того, что не учитываются результаты учения тех из них, кто пришел в данный класс во время между двумя измерениями (или, наоборот, перешел в другой класс или школу), пропустил много занятий по болезни.
При изучении больших по объему совокупностей проблема отбора решается с учетом количественной и качественной представительности выборки, это называется требованием репрезентатив ности.
Во-первых, следует определить минимальное число объектов, необходимых для того, чтобы при измерении их характерных особенностей начал действовать закон больших чисел или условие массовости выборки. Соблюдение данного условия необходимо для получения надежных выводов.
Во-вторых, требуется обдумать соблюдение качественной представительности выборки. Под качественной представительностью выборки понимается подбор такой группы объектов, в которой отражены все основные свойства генеральной совокупности.
Репрезентативная выборка имеет достаточно большой объем и отражает основные свойства генеральной совокупности. Требование репрезентативности соблюдается лишь при случайном отборе объектов в выборке.
Метод случайного отбора характеризуется двумя отличительными особенностями: 1) каждый объект генеральной совокупности имеет одинаковый шанс быть избранным; 2) отбор одного объекта не влияет на отбор какого-либо другого объекта. К данному методу относятся следующие виды отбора: простой случайный отбор, отбор методом случайных чисел, стратифицированный отбор, систематический отбор.
Простой случайный отбор применяют в тех случаях, если выборка составляется из совокупности небольшого объема. Каждому элементу совокупности присваивается порядковый номер. Все номера записываются на одинаковые карточки, которые тщательно перемешиваются. Затем выбирается число карточек, требуемое объемом выборки. Выборку составят те объекты, порядковые номера которых оказались на вынутых карточках.
Отбор методом случайных чисел отличается от предыдущего только процессом отбора карточек. При отборе карточек применяется таблица случайных чисел. С любого места таблицы выписывают столько случайных чисел, сколько объектов необходимо взять в выборку. Те объекты, порядковые номера которых соответствуют этим числам, составят нужную выборку. Данный метод отбора учащихся непригоден при объеме генеральной совокупности боль-
263
ше 1 тыс. учащихся из-за большой сложности в организации и финансового обеспечения усилий многих людей.
Стратифицированный отбор необходим, если рассматриваются некоторые качественные или количественные характеристики отдельных групп изучаемой совокупности. Например, требуется исследовать учащихся младших, средних и старших классов, а также учащихся с плохой, средней и хорошей успеваемостью с учетом их места жительства в городе или сельской местности. Во избежание увеличения объема выборки стратифицированный отбор предполагает обследование каждой из этих групп учащихся в отдельности с последующим объединением результатов обследования.
Методика стратифицированного отбора включает в себя три этапа:
1) деление совокупности на типические группы (страты);
2) составление случайной выборки из каждой страты;
3) объединение статистических оценок, полученных по каждой выборке, в составную статистическую оценку, взвешенную пропорционально объему страт.
Систематический (систематизированный, интервальный) отбор заключается в том, что выборку из совокупности производят путем отбора объектов через фиксированный интервал, что можно применить при исследовании упорядоченных объектов (таких, например, как пачка тетрадей с контрольными работами) или переписанных объектов (список фамилий учащихся).
Использование метода систематического отбора может привести к ошибочным выводам, если объекты совокупности расположены в циклическом порядке (например, в стопке тетрадей контрольные работы каждого класса сложены по оценкам: сначала отличные работы, затем хорошие, посредственные и неудовлетворительные). При совпадении величины интервала отбора с периодом цикла (например, в середине каждой пачки находятся посредственные работы) в выборку могут попасть объекты, которые составят непредставительную выборку.
К методам неслучайного отбора относятся бессистемный отбор, доступная и целенаправленная выборки.
Бессистемный отбор заключается в изучении объектов, случайно встретившихся исследователю.
Доступная выборка составляется из объектов, изучение которых находится в возможностях исследователя; от предыдущего отличается систематизированностью.
Целенаправленная выборка составляется в тех случаях, когда исследователь прибегает при отборе объектов измерения к помощи лица, хорошо знающего всех членов совокупности (например, учителя или директора).
В процессе психолого-педагогического исследования невозможно устранить влияние всех случайных или не подлежащих изуче-
264
нию факторов на конечные результаты. Очень большое множество как объективных, так и субъективных факторов оказывают воздействие в ходе эксперимента на те или иные стороны учебно-воспитательного процесса. Это влияние может быть ограничено, если при составлении выборки учащихся будут соблюдаться следующие условия: объем выборки устанавливается в зависимости от цели исследования и составляет достаточно большую часть объема той совокупности, которая подлежит изучению; объекты измерения максимально вариативны по состоянию измеряемого признака; объекты измерения максимально однородны по состоянию общих (не подлежащих изучению) признаков; выводы, полученные на основе изучения репрезентативной выборки, можно распространить на учащихся, не включенных в выборку, если они принадлежат к той же совокупности, из которой сделана выборка.
Дисперсия, стандартное и среднее отклонения. Меры центральной тенденции говорят о концентрации группы значений на числовой шкале. Каждая мера дает такое значение, которое представляет все оценки группы. При этом пренебрегают различиями, существующими между отдельными значениями. Для измерения вариации оценок внутри группы требуются описательные статистические методы: дисперсия, стандартное отклонение, среднее отклонение.
Некоторые из наиболее важных функций статистики связаны с процедурами, позволяющими уменьшить, объяснить или интерпретировать изменчивость, которая в известном смысле является неопределенностью. Всякая научная деятельность связана с понятием изменчивости. Когда есть много необъяснимых причин вариабельности, прогнозы не будут очень точными. Зато когда объяснения причин различий, каких-либо характеристик у учащихся (учителей) представлены в виде модели, неопределенность можно уменьшить, а часть вариаций устранить.
Например, если бы было совсем неизвестно, почему люди различаются между собой по умственному развитию, то попытка прогнозировать интеллект наталкивалась бы на большую неопределенность: некоторые люди выглядели бы «смышлеными», а другие — «глупыми», и никто не знал бы почему. Однако если известно, что наследственность и окружающая среда оказывают количественное влияние на Ю, то информация о происхождении ребенка и его воспитании в раннем детстве позволила бы дать более точный прогноз его умственного развития в зрелости. Другими словами, вариабельность Ю у лиц со сходной наследственностью и окружающей средой меньше, чем у людей вообще.
Дисперсия показывает значение отклонения, которое несет информацию о вариации совокупности значений. Совокупность с
965
большой неоднородностью будет иметь несколько больших отклонений. Каковы были бы отклонения, если бы все значения в совокупности равнялись 9? Каждое отклонение равнялось бы нулю, т. е. в предельно однородной совокупности все отклонения равны нулю.
Разброс полученных данных в положительную и отрицательную стороны от средней величины представляет собой ее среднюю арифметическую всех отклонений, зафиксированных в диагностируемой группе, и вычисляется путем сложения их значений и деления на количество испытуемых. Чем больше ее средняя арифметическая, тем больше разброс данных и тем более разнородна выборка. Если ее средняя арифметическая невелика, то это свидетельствует в пользу того, что данные близки к среднему значению и выборка более однородна.
Вычисление среднего отклонения в выборке из 6 элементов проводится следующим образом.
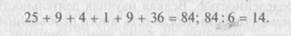
В результате такого расчета получают дисперсию.
Из дисперсии извлекается квадратный корень, и получается стандартное отклонение. В данном примере стандартное отклонение равно 3,74.
Чтобы более точно оценить стандартное отклонение для малых выборок (с числом элементов менее 30), в знаменателе выражения под корнем надо использовать не п, а п - 1. Стандартное отклонение рассчитывается по формуле:
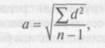
где а1 — дисперсия, п — количество элементов выборки.
Стандартное отклонение показывает, как далеко в положительную и отрицательную стороны от средней разбросаны результаты, а также укладывается ли этот разброс результатов в стандартное отклонение, которое равно 68 % популяции.
266
Степень корреляции значений двух переменных может быть вычислена двумя способами: с применением параметрических и непараметрических методов (тестов). Наиболее широкое применение находят параметрические методы, когда возможно сравнение распределения средних показателей параметров, таких, как среднее арифметическое или дисперсия данных. Непараметрические методы (когда среднее арифметическое неприменимо) используют в том случае, когда исследователь имеет дело с очень малыми выборками или с качественными данными; их достоинство — в простоте расчетов и применения.
Обоснованный выбор как параметрических, так и непараметрических методов в процессе психолого-педагогического исследования во многом определен полученными экспериментальными данными.
Статистическая гипотеза. Статистической гипотезой называется предположение относительно сходства или различия функциональных и числовых характеристик случайных величин или событий.
Статистические гипотезы в психолого-педагогических исследованиях делят на четыре основные группы:
1) гипотезы о типах вероятностных законов распределения случайных величин;
2) гипотезы о свойствах тех или других числовых параметров;
3) гипотезы о стохастической (вероятностной) зависимости двух или более признаков (факторов);
4) гипотезы о равенстве или различии законов распределения случайных величин, характеризующих изучаемое свойство в двух или более совокупностях рассматриваемых явлений.
В математической статистике проверка гипотез о случайных величинах и событиях базируется на принципе так называемой практической невозможности событий. Сущность данного принципа в том, что задается заранее некоторая вероятность а (например, а = 0,10; а = 0,05), именуемая уровнем значимости. При этом случайные события, вероятность которых меньше или равна а, считаются практически невозможными, но если они происходят, то наступление этого рода событий следует рассматривать как неслучайное. Такое событие становится для нас значимым. Выявлена следующая закономерность: чем меньше расчетная вероятность осуществления события, тем больше его неслучайность и тем важнее раскрыть принципы этой закономерности.
Уровень значимости, выраженный в процентах, показывает, в скольких случаях из 100 мы можем ошибиться, объявив изучаемое событие неслучайным. В гуманитарных науках общепринят 5-процентный уровень значимости, при котором допускается ошибка в 5 случаях из 100. При более высоком уровне значимости (10-процентном) большее число событий нельзя рассматри-
267
вать как неслучайные, но достоверность такого вывода будет ниже (90 % против 95 %). Наоборот, более низкий уровень значимости (1-, 0,999-процентный) приводит к более осторожным, но и более достоверным выводам.
Статистическая гипотеза представляет собой утверждение, которое объективно может оказаться либо истинным, либо ложным. Следовательно, уже на этапе выдвижения гипотезы мы обязаны одновременно и отрицать ее в форме противоположной (альтернативной) гипотезы.
Подлежащую контролю гипотезу называют гипотезой частот или нулевой гипотезой. Согласно нулевой гипотезе, существует равенство теоретических вероятностей двух предположений Рг и Р2. Справедливость гипотезы означает, что наблюдаемое различие частот объясняется случайными причинами.
Нулевой гипотезе противопоставляется альтернативная гипоте за. Альтернативной является рабочая гипотеза научного исследования, согласно которой наблюдаемое различие частот неслучайно, значимо, обусловлено влиянием независимой переменной. Основной принцип метода проверки гипотез заключается в том, что нулевая гипотеза выдвигается для того, чтобы попытаться опровергнуть ее и тем самым подтвердить альтернативную гипотезу.
Чтобы судить о вероятности ошибки при выборе позиции относительно нулевой гипотезы, применяют статистические методы, соответствующие особенностям выборки. Так, для количественных данных при распределениях, близких к нормальным, используют параметрические методы, основанные на таких показателях, как средняя величина и стандартное отклонение. При работе с неколичественными данными или слишком малыми выборками для уверенности в том, что популяции, из которых они взяты, подчиняются нормальному распределению, используют непараметрический метод — коэффициент корреляции Пирсона для качественных данных.
От того, являются ли выборки, средние величины которых сравниваются, независимыми (например, взятыми из двух разных групп испытуемых) или зависимыми (т. е. отражающими результаты одной и той же группы испытуемых до и после воздействия или после двух различных воздействий), также зависит выбор статистического метода.
Дата: 2018-12-21, просмотров: 261.
