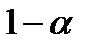При формализации процесса функционирования системы TСН используется наиболее общий метод преобразований, метод интегральных уравнений. Решение задачи по оценке надежности системы ТСН заключается в отыскании минимального значения целевой функции 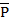 (t ). В этой связи интегральные уравнения составляются для процесса восстановления системы ТСН на таком интервале времени [t ,t+τ] на котором отказ системы ТСН имеет наибольшую вероятность, т.е.
(t ). В этой связи интегральные уравнения составляются для процесса восстановления системы ТСН на таком интервале времени [t ,t+τ] на котором отказ системы ТСН имеет наибольшую вероятность, т.е. 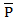 (t ) ® min.
(t ) ® min.
Метод дифференциальных уравнений при формализации процесса функционирования системы ТСН не применяется по тем причинам, что данный метод основан на допущении постоянства λ и µ для каждого элемента системы ТСН на интервале времени [t, t+τ]при t→∞, где λи µ - интенсивность отказа и интенсивность восстановления элемента, имеющего показательное распределение наработки на отказ и показательное распределение времени восстановления.
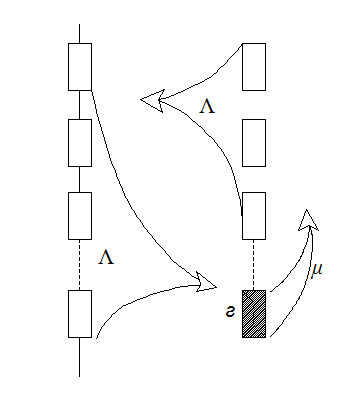
Рис.6.21.
В отдельных случаях допущение постоянства λ и μ для насосной установки не сильно влияют на характеристики надежности системы ТСН. Однако, для решения поставленной задачи такое допущение противоречит не только физике, но и логическому описанию процесса функционирования системы ТСН. В этом не трудно убедиться, если рассмотреть логическую схему функционирования системы TВH, у которой m+n однотипных элементов (см. рис. 6.21 и 6.22 ).
| P |
| 1 2 ….. Z 1 2 …. Z |
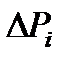
|
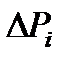
|
| t |
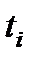 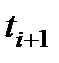 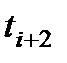
|
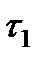
|
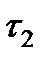
|
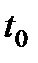
|
Рисунок 6.22. Логическая схема процесса восстановления системы при λ=const, µ=const, r =1, m>1
Система непрерывно работает на отрезке времени [0, t] и восстанавливается одной ремонтной единицей r= 1. В момент t=to m элементов включаются в работу (рис. 6.22 ), а остальные n элементов , находясь в холодном резерве, ждут своей очереди. Через некоторое случайное время t i работающий элемент отказывает, и в работу включается первый резервный элемент, а отказавший элемент ставится на восстановление. Система продолжает выполнять свои функции, но ее надежность уменьшается на величину ΔРi . Предполагаем, что ремонтная единица может одновременно восстанавливать не более 1 элемента за время τ.
1. Допустим, что для каждого элемента системы ТСН выполняется условие λ = const, μ = const
Если за время τ1 возможно появление такого числа отказавших элементов, у которого математическое ожидание равно Ζ , то вероятность безотказной работы системы ТСН снизится еще на величину 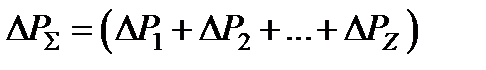 .
.
При Ζ>1 период регенерации системы ТСН может состоять из бесконечно большого числа шагов, т.к. ремонтная единица за время τi будет восстанавливать по одному элементу, а в системе ТСН будет накапливаться по Z -1 отказавших элементов. Но тогда вероятность безотказной работы системы ТСН 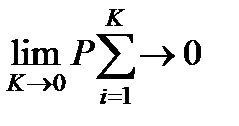
Следовательно, 1 допущение не удовлетворяет условиям решения рассматриваемой задачи.
2. Допустим, что у каждого элемента системы ТСH:
λ(t) - возрастающая функция интенсивности /ВФИ/;
µ(t) - возрастающая функция интенсивности /ВФИ/;
µ(t)>λ(t).
При таких допущениях система ТСН может регенерироваться, т.к. с увеличением суммарной интенсивности отказов элементов L= 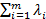 будет возрастать и µ(t), причем max µ(t) > 1>
будет возрастать и µ(t), причем max µ(t) > 1> 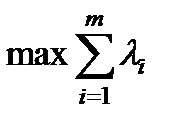 (состав ремонтной бригады, режим ее работы будет меняться с учетом сложившихся условий).
(состав ремонтной бригады, режим ее работы будет меняться с учетом сложившихся условий).
Допущение непостоянства λ и μ для элемента любой системы весьма сильно, но оно не позволяет получить решение задачи по определению вероятности безотказной работы системы в замкнутой форме [21].
Поэтому для частного решения задачи по оценке Р(τ) системы TСН , естественно применение модели со следующими допущениями:
1) в системе "ТСН" элементы не отказывают и не меняют параметры в состоянии резерва (хранения);
2) каждый элемент изменяет свои состояния по графу pиc. 6.23.
| 1 |
| 2 |
| 5 |
| 4 |
| 3 |
Рисунок 6.23 . Граф состояний системы ТСН
1- работа, 2- отказ, 3- ожидание восстановления, 4- восстановление,
5- пребывание в резерве.
3) каждый элемент восстанавливается либо при наработке t, либо в момент отказа, если он происходит раньше ;
4) отказ наступает в момент, когда восстанавливается и стоят в очереди на восстановление n +с элементов;
5) время наработки на отказ элемента распределяется по закону Вейбулла, а время восстановления после отказа - по закону Эрланга 2-го порядка,
Для экстремального определения целевой функции 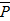 ( t ) рассмотрим функционирование системы ТСН на таком отрезке времени, на котором ремонтная единица занята восстановлением отказавшего элемента, а суммарная интенсивность отказов основных элементов Λ принимает значение
( t ) рассмотрим функционирование системы ТСН на таком отрезке времени, на котором ремонтная единица занята восстановлением отказавшего элемента, а суммарная интенсивность отказов основных элементов Λ принимает значение 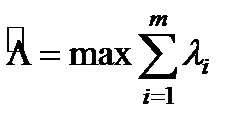 .
.
Вероятность безотказной работы системы ТCН на отрезке времени [0, ∞] может оцениваться по формуле:
, 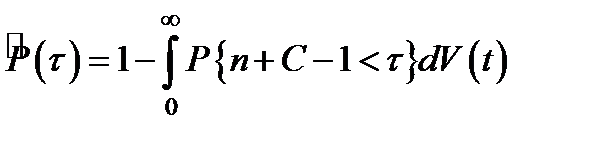 ,
,
где 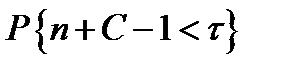 - вероятность того, что за время занятости ремонтной единицы откажут n +с-1 элементов ;
- вероятность того, что за время занятости ремонтной единицы откажут n +с-1 элементов ;
V(τ) - функция времени восстановления элемента,
Выполненные статистические исследования позволяют допустить, что у системы ТСН:
1) время ∆t= τ , за которое оценивается вероятность безотказной работы, не превышает среднего времени безотказной работы элемента To ;
2) суммарная интенсивность отказов элементов Λ принимает на отрезке времени τ=Tв максимальное значение 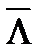 .
.
Верхняя оценка вероятности простоя в очереди на восстановление n+с -1 элементов системы TСH может быть определена по формуле [10, 21]
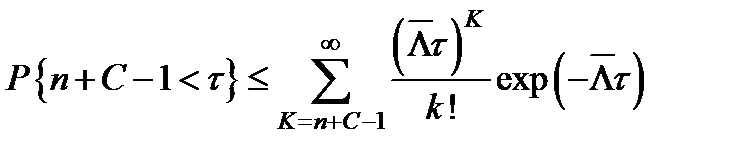 ,
,
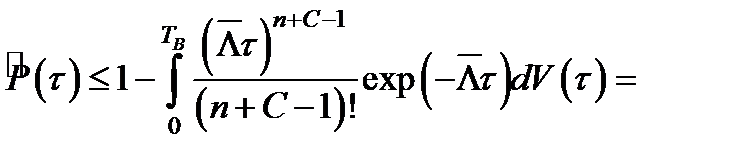
= 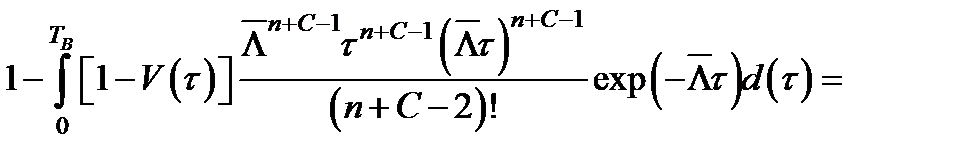
= 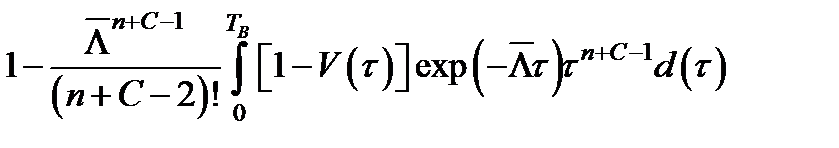
где 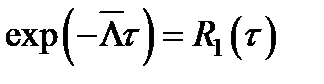 - вероятность того, что промежуток времени между двумя последовательными моментами наступления событий стационарного потока без последействия превзойдет τ (вероятность, что за время τ элемент восстановиться и система ТСН не откажет ) ;
- вероятность того, что промежуток времени между двумя последовательными моментами наступления событий стационарного потока без последействия превзойдет τ (вероятность, что за время τ элемент восстановиться и система ТСН не откажет ) ;
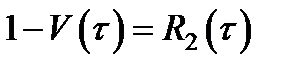 - вероятность того, что элемент не восстановится за время τ.
- вероятность того, что элемент не восстановится за время τ.
В системе ТСН для восстановления элементов применяется ручной труд. Данное обстоятельство существенно влияет на характер процесса восстановления системы ТСН (он не является уже полностью случайным процессом). Поэтому можно предположить, что в момент, когда 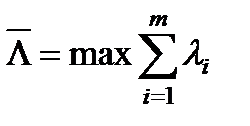 наступает равновесие τ = Tв (т.е. за время более, чем n+С-1 элементов не откажут) и процесс восстановления системы ТCН приобретает свойства потока, параметры которого детерминированы.
наступает равновесие τ = Tв (т.е. за время более, чем n+С-1 элементов не откажут) и процесс восстановления системы ТCН приобретает свойства потока, параметры которого детерминированы.
Кроме того, если общий поток событий соответствует модели экспоненциального распределения, то: , 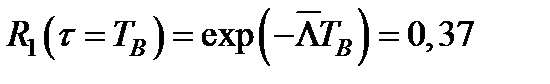
, 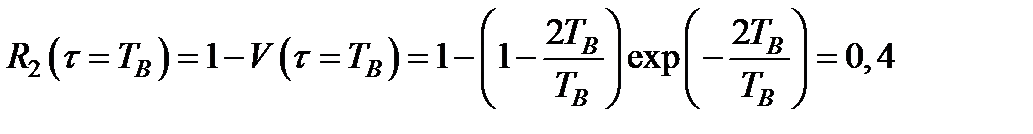
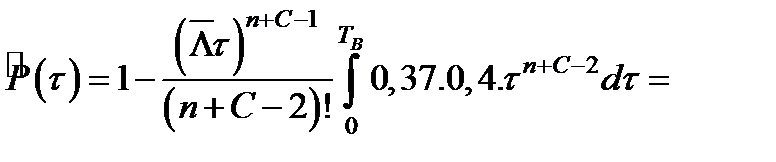
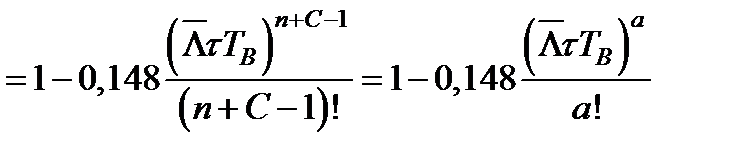
где а - число появлений событий (отказы, остановки на ремонт насосных установок).
Очевидно, элементы в системе ТСН могут работать как постоянно, так и переменно в течение суток; они могут ремонтироваться и заменяться на новые. Условное число непрерывно работающих элементов в системе ТСН можно определить по формуле
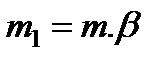
где 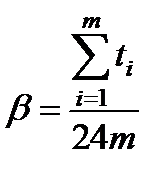
m - число основных элементов в системе ТСН
ti - время работы i -го -элемента в системе ТCН в сутки, которое оценивается по графику режима работы насосной станции.
В этой связи искомую математическую модель надежности системы ТСН можно представить в виде:
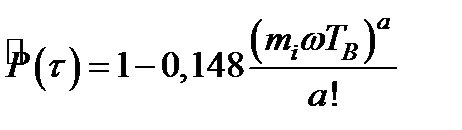
где 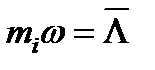
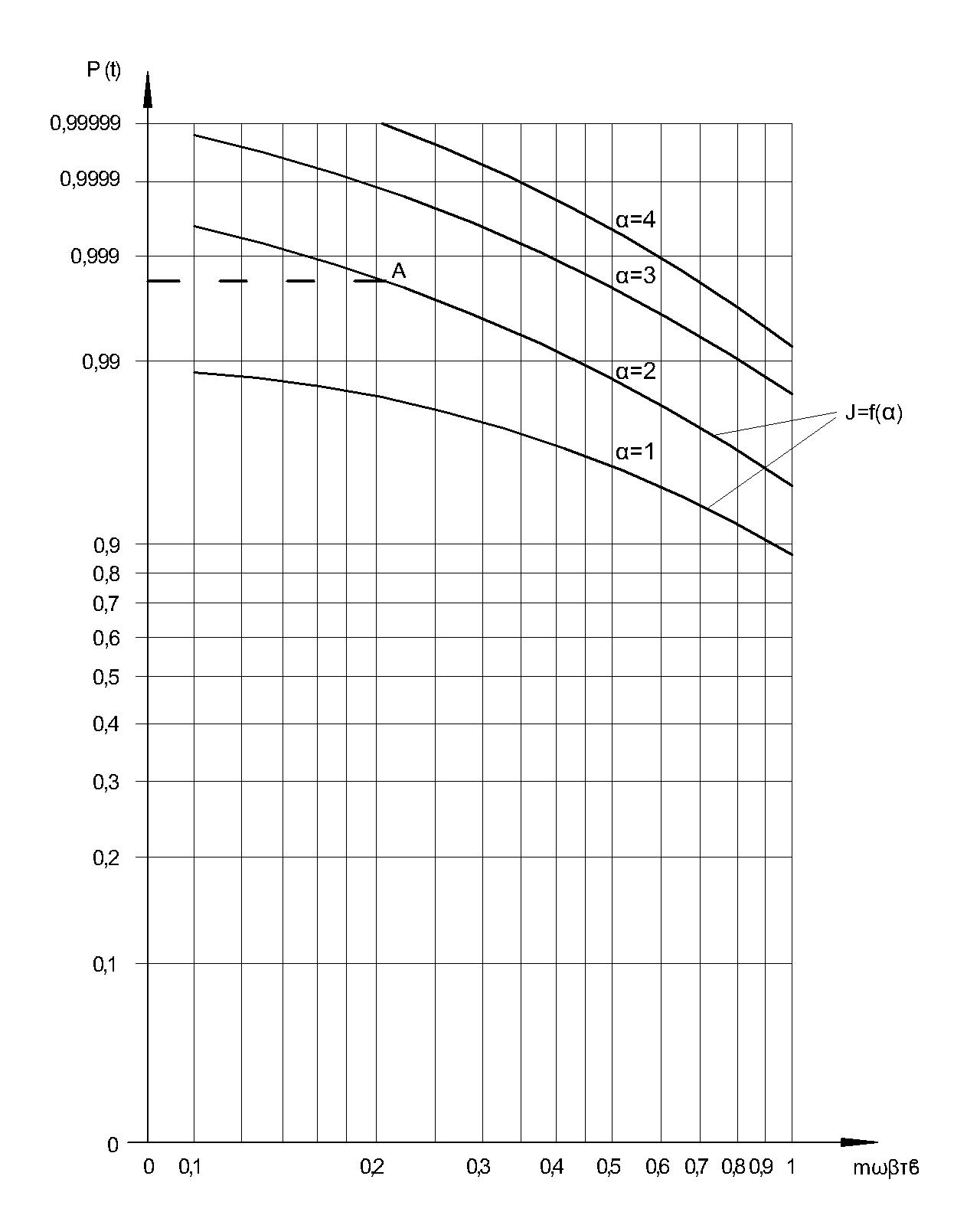
Рис. 6.24 . Номограмма для определения числа резервных насосных установок на насосной станции при заданных параметрах: m, ω, n, β, Tв и r=1
Для упрощения расчетов надежности системы ТСН по формулам предлагается номограмма, которая приведена на рис. 6.24 .
Номограмма имеет логарифмические шкалы: на оси ординат откладываются значения вероятности безотказной работы системы ТСН
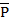 (t) (уровни надежности), а по оси абсцисс значения-вида m, ω, β, Tв. Восстанавливая перпендикуляр, например, из точки М до пересечения с кривой J=f (a) и проводя горизонталь через точку пересечения "А" (рис.6.24 ) на оси ординат находят значения
(t) (уровни надежности), а по оси абсцисс значения-вида m, ω, β, Tв. Восстанавливая перпендикуляр, например, из точки М до пересечения с кривой J=f (a) и проводя горизонталь через точку пересечения "А" (рис.6.24 ) на оси ординат находят значения 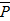 ( t ) . Если известны
( t ) . Если известны 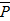 ( t ), m, ω, β, Tв, а неизвестно значение n , то операции выполняются в обратном порядке.
( t ), m, ω, β, Tв, а неизвестно значение n , то операции выполняются в обратном порядке.
Литература
1.Абрамов Н.Н. Надежность систем водоснабжения. // Стройиздат. М. 1979
2.Барлоу Р., Прошан Ф. Математическая теория надежности. // "Советское радио" М.,1969
3. Базовский И. Надежность. Теория и практика. // "Мир". М., 1965.
4. Волков П.Н. Элементы теории вероятностей и математической статистики. //МАДИ. М. , 1970.
5. Вентцель Е.С. Теория Вероятностей. //"Наука". М., 1969.
6. ГОСТ 27.002-89. "Надежность в технике. Термины и определения" М., 1989
7. ГОСТ Р 53480-2009. "Надежность в технике. Термины и определения" М., 2009
8. ГОСТ 27.003-83. Выбор и нормирование показателей надежности. М., 2009
9. ГОСТ 11.007-75. Правила определения оценок т доверительных границ для параметров распределения Вейбулла. М., 1976.
10. Гнеденко Б.В., Беляев Ю.К., Соловьев А.Д. Математические методы в теории надежности. //"Наука". М. , 1965.
11. Груничев А.С, Михайлов А.И., Шор Я.Б. Таблицы для расчетов надежности при распределении Вейбулла. //Издательство стандартов. М., 1974.
12. Дерюшев Л.Г. Оценка надежности технологических систем водопроводных насосных станций. //Диссер. на соискание уч. ст. канд. техн. наук. М.,1979
13. Дерюшев Л.Г. Показатели надежности трубопроводных систем водоснабжения и водоотведения. //Водоснабжение и сан. техника. 2000. №12
14. Д ерю ш ев JI. Г., Минаев А. В. О вопросах оценки надежности трубопроводных систем водоснабжения. // Надежность водопроводных систем: Тезисы докладов. МДНТП М., 1988.
15. Дунин-Барковский И.В., Смирнов Н.В. Теория вероятностей и математическая статистика в технике (общая часть). // Технико-теоретическая литература. М. , 1955
16. Ильин Ю.А. Расчет надежности подачи воды. // Стройиздат. М., 1987.
17. Нормы амортизационных отчислений. // Госплан СССР . М.., 1977.
18. Методические указания. Методика выбора номенктлатуры нормируемых показателей надежности технических устройств. МУ 3-69. М.,1970.
19. Положение о составе разделов проектной документации и требования к их содержанию. (Постановление Правительства РФ от 18.05.2009 № 427)
20. Проблемы надежности систем водоснабжения: Тез. докл. Всесоюз. конф. по надежности систем водоснабжения. // М., МИСИ, 1973.
21. СП 31.13330.2012 Водоснабжение. Наружные сети и сооружения. М., 2012.
22. СНиП 2.01.14-83. Определение расчетных гидрологических характеристик. М., 1985.
23. Соловьев А.Д. в. Основы математической теории надежности. // Государственный комитет стандартов Совета министров СССР. М.,1975. Вып.1,2,3.
24. X е р ц Р. К. Процесс старения и необходимость восстановления водопроводных сетей // АКВА. 1996. № 5.
25. Хевиленд Р. Инженерная надежность и расчет на доловечность. // М., Энергия, 1966.
26. Ястребенецкий М.А. Соляник В.Л. Определение надежности аппаратуры промышленной автоматики в условиях эксплуатации. // М., Энергия., 1968
ПРИЛОЖЕНИЕ 1
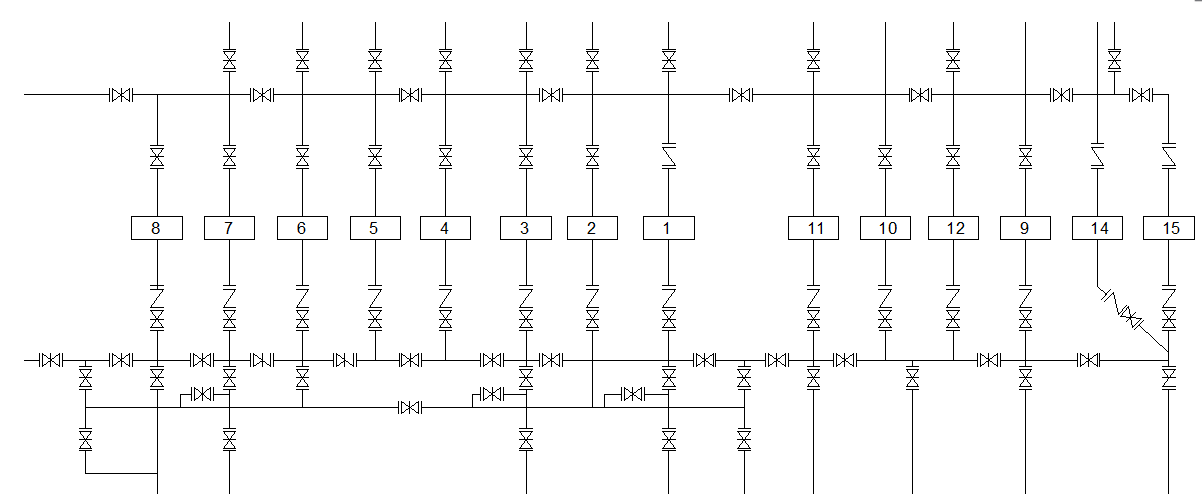
Рис 1. Технологическая схема насосной станции №1 г.1
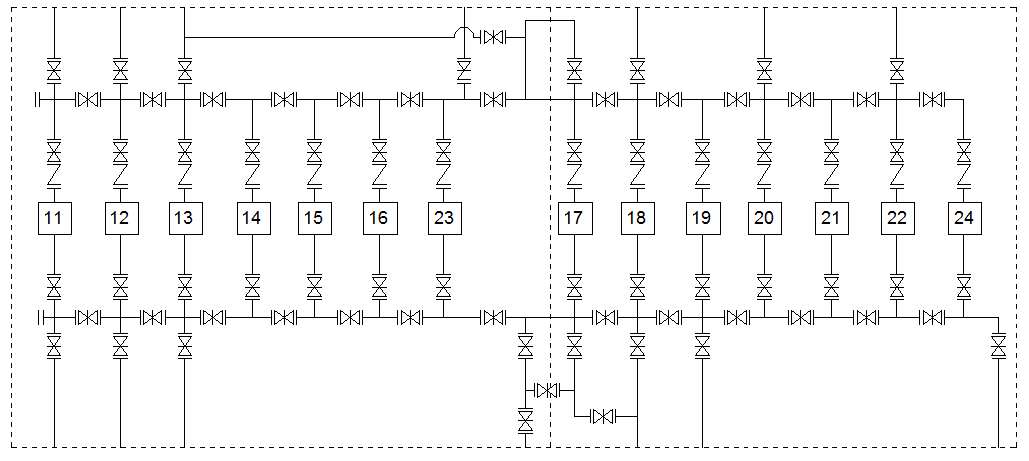
Рис 2. Технологическая схема насосной станции №2 г.2
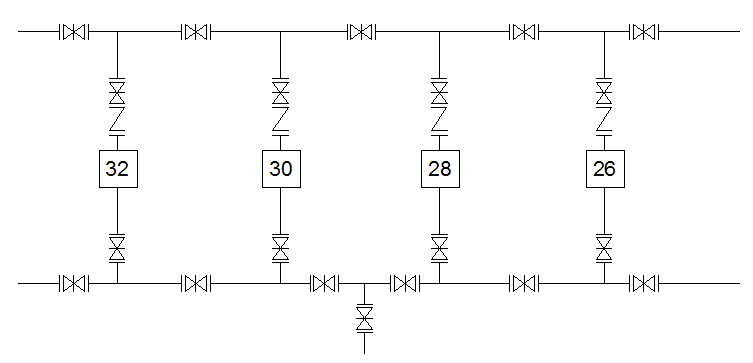
Рис 3. Технологическая схема насосной станции №3 г.1
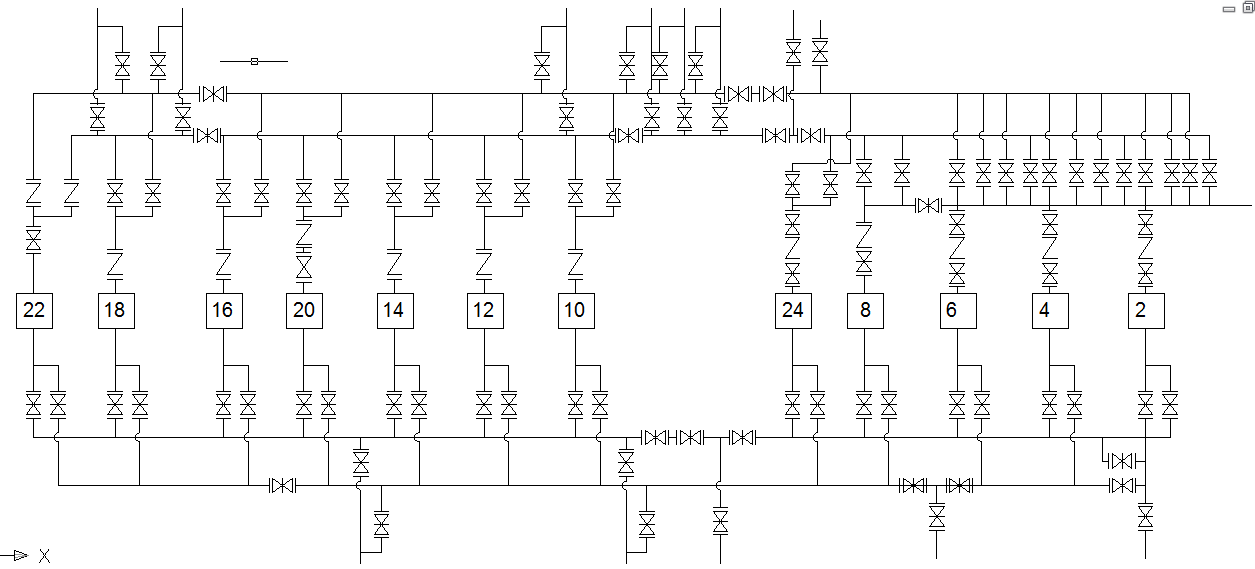
Рис 4. Технологическая схема насосной станции №4 г.1
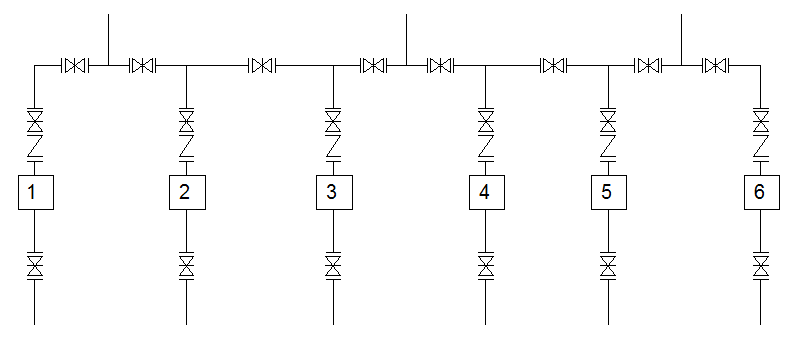
Рис 5. Технологическая схема насосной станции №2 г.2
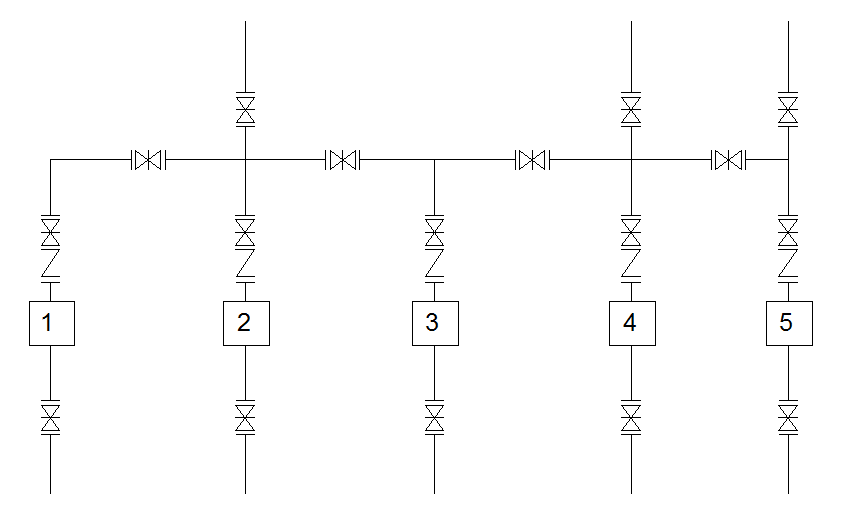
Рис 6. Технологическая схема насосной станции №1 г.3
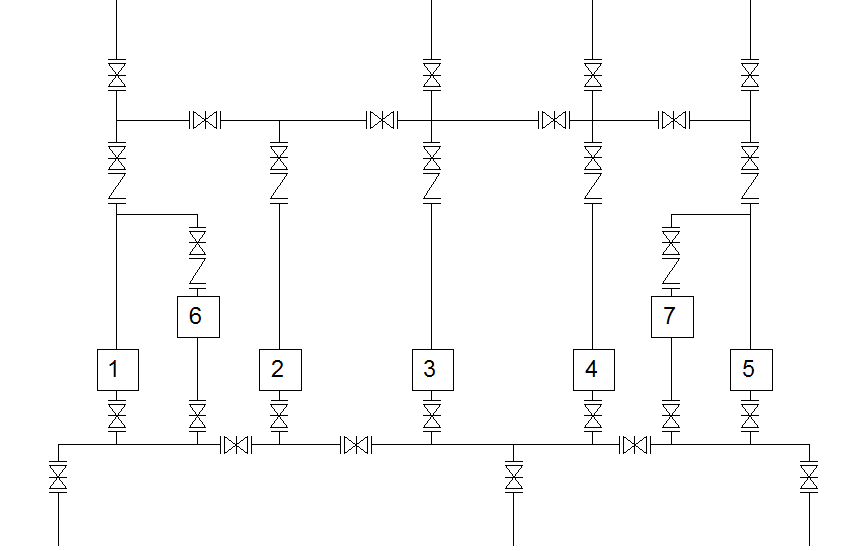
Рис 7. Технологическая схема насосной станции №2 г. 3
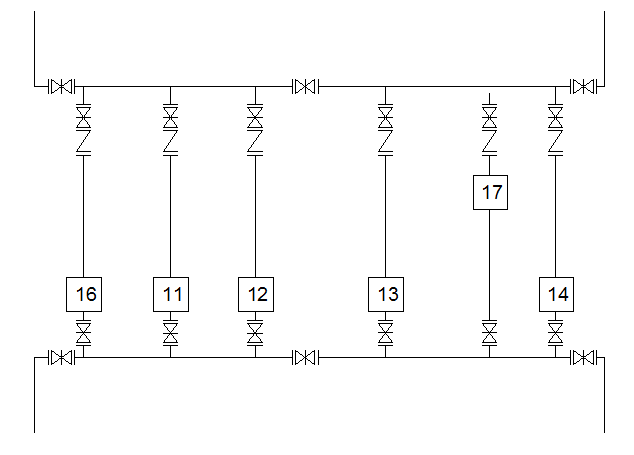
Рис 8. Технологическая схема насосной станции №3 г.3
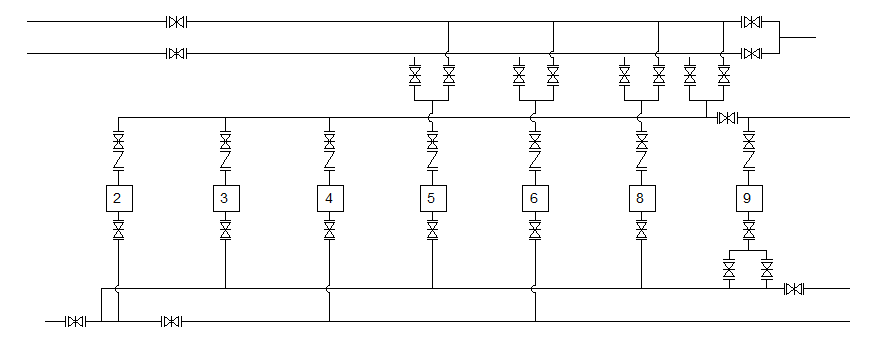
Рис 9. Технологическая схема насосной станции №4 г.3
ПРИЛОЖЕНИЕ 2
Таблица 1
Плотность вероятности нормированного нормального распределения 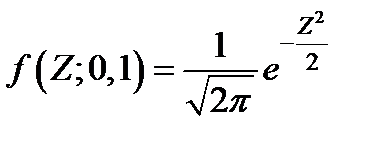
| Z |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0.0 | 0 | 3989 | 3989 | 3989 | 3988 | 3986 | 3984 | 3982 | 3980 | 3977 | 3973 |
| 0.1 | 0 | 3970 | 3965 | 3967 | 3956 | 3951 | 3945 | 3933 | 3932 | 3925 | 3918 |
| 0.2 | 0 | 3910 | 3902 | 3824 | 3885 | 3876 | 3867 | 3857 | 3847 | 3835 | 3825 |
| 0.3 | 0 | 3874 | 3802 | 3790 | 3778 | 3765 | 3752 | 3733 | 3725 | 3712 | 3697 |
| 0.4 | 0 | 3633 | 3668 | 3653 | 3637 | 3621 | 5505 | 3589 | 3572 | 3555 | 3538 |
| 0.5 | 0 | 3521 | 3503 | 3485 | 3467 | 3448 | 3429 | 3410 | 3391 | 3372 | 3352 |
| 0.6 | 0 | 3332 | 3312 | 3292 | 3271 | 3251 | 3230 | 3209 | 3187 | 3166 | 3144 |
| 0.7 | 0 | 3123 | 3101 | 3075 | 3055 | 3034 | 3011 | 2989 | 2555 | 2943 | 2926 |
| 0.8 | 0 | 2897 | 2874 | 2850 | 2827 | 2803 | 2720 | 2755 | 2732 | 2705 | 2585 |
| 0.9 | 0 | 2661 | 2537 | 2513 | 2589 | 2565 | 2541 | 2516 | 2492 | 2458 | 2444 |
| 1.0 | 0 | 2420 | 2396 | 2371 | 2347 | 2323 | 2299 | 2275 | 2251 | 2227 | 2263 |
| 1.1 | 0 | 2179 | 2155 | 2131 | 2107 | 2083 | 2059 | 2036 | 2012 | 1989 | 1955 |
| 1.2 | 0 | 1942 | 1919 | 1895 | 1872 | 1849 | 1826 | 1804 | 1781 | 1758 | 1736 |
| 1.3 | 0 | 1714 | 1691 | 1669 | 1647 | 1626 | 1604 | 1582 | 1561 | 1539 | 1518 |
| 1.4 | 0 | 1497 | 1476 | 1456 | 1435 | 1415 | 1594 | 1374 | 1354 | 1334 | 1315 |
| 1.5 | 0 | 1295 | 1276 | 1257 | 1238 | 1219 | 1200 | 1182 | 1163 | 1145 | 1127 |
| 1.6 | 0 | 1109 | 1092 | 1074 | 1057 | 1040 | 1023 | 1006 | 989 | 973 | 957 |
| 1.7 | 0.0 | 9405 | 9246 | 9089 | 8933 | 8780 | 8628 | 8478 | 8329 | 8183 | 8038 |
| 1.8 | 0.0 | 7895 | 7754 | 7614 | 7477 | 7341 | 7256 | 7074 | 6943 | 6814 | 6687 |
| 1.9 | 0.0 | 6562 | 6438 | 6316 | 6195 | 6077 | 5959 | 5844 | 5730 | 5618 | 5508 |
| 2.0 | 0.0 | 5399 | 5292 | 5186 | 5082 | 4980 | 4879 | 4780 | 4582 | 4586 | 4491 |
| 2.1 | 0.0 | 4398 | 4307 | 4217 | 4128 | 4041 | 3955 | 3871 | 3788 | 3705 | 3626 |
| 2.2 | 0.0 | 3547 | 3470 | 3394 | 3319 | 3245 | 3174 | 3103 | 3034 | 2965 | 2398 |
| 2.3 | 0.0 | 2833 | 2768 | 2705 | 2643 | 2582 | 2522 | 2463 | 2406 | 2349 | 2294 |
| 2.4 | 0.0 | 2239 | 2186 | 2134 | 2083 | 2033 | 1984 | 1936 | 1888 | 1842 | 1797 |
| 2.5 | 0.0 | 1753 | 1709 | 1667 | 1625 | 1585 | 1545 | 1505 | 1468 | 1431 | 1394 |
| 2.6 | 0.0 | 1358 | 1324 | 1289 | 1256 | 1223 | 1191 | 1160 | 1130 | 1100 | 1071 |
| 2.7 | 0.0 | 1042 | 1014 | 987 | 951 | 935 | 909 | 885 | 861 | 837 | 814 |
| 2.8 | 0.00 | 7915 | 7696 | 7483 | 7274 | 7071 | 6873 | 6679 | 8491 | 6357 | 6127 |
| 2.9 | 0.00 | 5952 | 5782 | 5616 | 5454 | 5295 | 5143 | 4993 | 4847 | 4705 | 4567 |
| 3.0 | 0.00 | 4432 | 4301 | 4173 | 4049 | 3928 | 3810 | 5625 | 3584 | 3475 | 3370 |
| 3.0 | 0.00 | 4432 | 3267 | 2384 | 1723 | 1232 | 873 | 6612 | 425 | 292 | 199 |
| 4.0 | 0.003 | 1338 | 893 | 539 | 385 | 249 | 160 | 101 | 64 | 40 | 24 |
| 5.0 | 0.005 | 1487 | 897 | 536 | 317 | 186 | 108 | 62 | 35 | 20 | 11 |
Таблица 2
Нормированная функция Лапласа 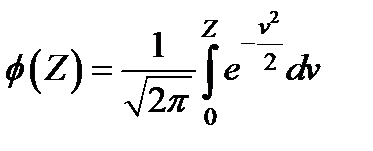
| Z | Сотые дали для Z | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0.0 | 0.0000 | 040 | 080 | 120 | 160 | 199 | 239 | 279 | 319 | 359 |
| 0.1 | 398 | 438 | 478 | 517 | 557 | 596 | 636 | 675 | 714 | 753 |
| 0.2 | 793 | 832 | 871 | 910 | 948 | 987 | 026 | 064 | 103 | 141 |
| 0.3 | 0.1179 | 217 | 255 | 293 | 331 | 368 | 406 | 443 | 480 | 517 |
| 0.4 | 554 | 591 | 628 | 664 | 700 | 736 | 772 | 808 | 844 | 879 |
| 0.5 | 915 | 950 | 985 | 019 | 054 | 088 | 123 | 157 | 190 | 224 |
| 0.6 | 0.2257 | 291 | 324 | 357 | 389 | 422 | 454 | 486 | 517 | 549 |
| 0.7 | 580 | 611 | 642 | 673 | 703 | 734 | 764 | 794 | 823 | 852 |
| 0.8 | 881 | 910 | 939 | 967 | 995 | 023 | 051 | 078 | 106 | 133 |
| 0.9 | 0.3159 | 186 | 212 | 238 | 264 | 289 | 315 | 340 | 365 | 389 |
| 1.0 | 413 | 437 | 461 | 485 | 508 | 583 | 554 | 577 | 599 | 621 |
| 1.1 | 643 | 665 | 686 | 708 | 729 | 749 | 770 | 790 | 810 | 830 |
| 1.2 | 849 | 869 | 888 | 907 | 925 | 944 | 962 | 980 | 997 | 015 |
| 1.3 | 0.4032 | 049 | 066 | 082 | 099 | 115 | 131 | 147 | 162 | 177 |
| 1.4 | 192 | 207 | 222 | 236 | 251 | 265 | 279 | 292 | 306 | 319 |
| 1.5 | 332 | 345 | 357 | 370 | 382 | 394 | 406 | 418 | 429 | 441 |
| 1.6 | 452 | 463 | 474 | 484 | 495 | 505 | 515 | 525 | 535 | 545 |
| 1.7 | 554 | 564 | 573 | 582 | 591 | 599 | 608 | 616 | 625 | 633 |
| 1.8 | 641 | 649 | 656 | 664 | 671 | 678 | 686 | 693 | 699 | 706 |
| 1.9 | 713 | 719 | 726 | 732 | 738 | 744 | 750 | 756 | 761 | 767 |
| 2.0 | 772 | 778 | 783 | 788 | 793 | 798 | 803 | 808 | 812 | 817 |
| 2.1 | 821 | 826 | 830 | 834 | 838 | 842 | 846 | 850 | 854 | 857 |
| 2.2 | 860 966 | 864 474 | 867 906 | 871 263 | 874 545 | 877 755 | 880 894 | 883 962 | 886 962 | 889 893 |
| 2.3 | 892 759 | 895 559 | 898 296 | 900 969 | 903 581 | 906 133 | 908 625 | 911 060 | 913 437 | 915 758 |
| 2.4 | 918 025 | 920 237 | 922 397 | 924 506 | 926 564 | 928 572 | 930 531 | 932 493 | 934 309 | 936 128 |
| 2.5 | 937 903 | 939 634 | 941 323 | 942 969 | 944 574 | 946 139 | 947 664 | 949 151 | 950 600 | 952 012 |
| 2.6 | 953 388 | 954 729 | 956 035 | 957 308 | 958 547 | 959 754 | 960 930 | 962 074 | 963 189 | 964 274 |
| 2.7 | 965 330 | 966 358 | 967 359 | 968 333 | 969 280 | 970 202 | 971 099 | 971 972 | 972 821 | 973 946 |
| 2.8 | 0.4974 449 | 975 229 | 975 988 | 976 726 | 977 443 | 978 140 | 978 818 | 979 476 | 980 116 | 980 730 |
| 2.9 | 981 342 | 981 929 | 982 498 | 983 052 | 983 589 | 984 111 | 984 618 | 985 110 | 985 588 | 986 051 |
| 3.0 | 986 501 | 986 938 | 987 361 | 987 772 | 988 171 | 988 558 | 988 933 | 989 297 | 989 650 | 989 992 |
| 3.1 | 990 324 | 990 646 | 990 957 | 991 260 | 991 553 | 991 836 | 992 112 | 992 378 | 992 636 | 992 886 |
| 3.2 | 993 129 | 993 363 | 993 590 | 993 810 | 994 024 | 994 230 | 994 429 | 994 623 | 994 810 | 996 991 |
| 3.3 | 995 166 | 995 335 | 995 499 | 995 658 | 995 811 | 995 959 | 996 103 | 996 242 | 996 376 | 996 505 |
| 3.4 | 996 631 | 996 752 | 996 869 | 996 982 | 997 091 | 997 197 | 997 299 | 997 398 | 997 493 | 997 585 |
| 3.5 | 997 674 | 997 759 | 997 842 | 997 922 | 997 999 | 998 074 | 998 146 | 998 215 | 998 282 | 998 347 |
| 3.6 | 998 409 | 998 469 | 998 527 | 998 583 | 998 637 | 998 689 | 998 739 | 998 787 | 998 834 | 998 879 |
| 3.7 | 998 922 | 998 964 | 999 004 | 999 043 | 999 080 | 999 116 | 999 150 | 999 184 | 999 216 | 999 247 |
| 3.8 | 999 274 | 999 305 | 995 333 | 999 359 | 999 385 | 999 409 | 999 433 | 999 456 | 999 478 | 999 499 |
| 3.9 | 999 519 | 999 539 | 999 557 | 999 575 | 999 593 | 999 609 | 999 625 | 999 641 | 999 655 | 999 670 |
| 4.0 | 999 683 | 993 696 | 999 709 | 999 721 | 999 733 | 999 744 | 999 755 | 999 765 | 999 775 | 999 784 |
| 4.1 | 999 793 | 999 802 | 999 811 | 999 819 | 999 826 | 999 834 | 999 841 | 999 848 | 999 854 | 999 861 |
| 4.2 | 999 867 | 999 872 | 999 878 | 999 883 | 999 888 | 999 893 | 999 898 | 999 902 | 999 907 | 999 911 |
| 4.3 | 999 915 | 999 918 | 999 922 | 999 925 | 999 929 | 999 932 | 999 935 | 999 938 | 999 941 | 999 943 |
| 4.4 | 999 946 | 999 948 | 999 951 | 999 953 | 999 955 | 999 957 | 999 959 | 999 961 | 999 963 | 999 964 |
| 4.5 | 999 966 | 999 968 | 999 969 | 999 971 | 999 972 | 999 973 | 999 974 | 999 976 | 999 971 | 999 978 |
| 5.0 | 999 997 |
|
|
|
|
|
|
|
|
|
Таблица 3
Значения квантилей Z a нормированного нормального распредления F( Z ; 0,1) = a (обратной функции Лапласа)
| a | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0.00 | -¥ | -3.09 | -2.88 | -2.75 | -2.65 | -2.58 | -2.51 | -2.46 | -2.41 | -2.37 |
| 0,01 | -2.33 | -2.29 | -2.26 | -2.23 | -2.20 | -2.17 | -2.14 | -2.12 | -2.10 | -2.07 |
| 0.02 | -2.05 | -2.03 | -2.01 | -0.200 | -1.98 | -1.96 | -1.94 | -1.93 | -1.91 | -1.90 |
| 0.03 | -1.88 | -1.87 | -1.85 | -1.84 | -1.83 | -1.81 | -1.80 | -1.79 | -1.77 | -1.76 |
| 0.04 | -1.75 | -1.74 | -1.73 | -1.72 | -1.71 | -1.70 | -1.68 | -1.67 | -1.66 | -1.65 |
| 0.05 | -1.64 | -1.64 | -1.63 | -1.62 | -1.61 | -1.60 | -1.59 | -1.58 | -1.57 | -1.56 |
| 0.06 | -1.55 | -1.55 | -1.54 | -1.53 | -1.52 | -1.51 | -1.51 | -1.50 | -1.49 | -1.48 |
| 0.07 | -1.48 | -1.47 | -1.46 | -1.45 | -1.45 | -1.44 | -1.43 | -1.43 | -1.42 | -1.41 |
| 0.08 | -1.41 | -1.40 | -1.39 | -1.39 | -1.38 | -1.37 | -1.37 | -1.36 | -1.35 | -1.35 |
| 0.09 | -1.34 | -1.33 | -1.33 | -1.32 | -1.32 | -1.31 | -1.30 | -1.30 | -1.29 | -1.29 |
| 0.10 | -1.28 | -1.28 | -1.27 | -1.26 | -1.26 | -1.25 | -1.25 | -1.24 | -1.24 | -1.23 |
| 0.11 | -1.23 | -1.22 | -1.22 | -1.21 | -1.21 | -1.20 | -1.20 | -1.19 | -1.19 | -1.18 |
| 0.12 | -1.18 | -1.17 | -1.17 | -1.16 | -1.16 | -1.15 | -1.15 | -1.14 | -1.14 | -1.13 |
| 0.13 | -1.13 | -1.12 | -1.12 | -1.11 | -1.11 | -1.10 | -1.10 | -1.09 | -1.09 | -1.09 |
| 0.14 | -1.08 | -1.08 | -1.07 | -1.07 | -1.06 | -1.06 | -1.05 | -1.05 | -1.05 | -1.04 |
| 0.15 | -1.04 | -1.03 | -1.03 | -1.02 | -1.02 | -1.02 | -1.01 | -1.01 | -1.00 | -1.00 |
| 0.16 | -0.99 | -0.99 | -0.99 | -0.98 | -0.98 | -0.97 | -0.97 | -0.97 | -0.96 | -0.96 |
| 0.17 | -0.95 | -0.95 | -0.95 | -0.94 | -0.94 | -0.93 | -0.93 | -0.93 | -0.92 | -0.92 |
| 0.18 | -0.92 | -0.91 | -0.91 | -0.90 | -0.90 | -0.90 | -0.89 | -0.89 | -0.89 | -0.88 |
| 0.19 | -0.88 | -0.87 | -0.87 | -0.87 | -0.86 | -0.86 | -0.86 | -0.85 | -0.85 | -0.85 |
| 0.20 | -0.84 | -0.84 | -0.83 | -0.83 | -0.83 | -0.82 | -0.82 | -0.82 | -0.81 | -0.81 |
| 0.21 | -0.81 | -0.80 | -0.80 | -0.80 | -0.79 | -0.79 | -0.79 | -0.78 | -0.78 | -0.78 |
| 0.22 | -0.77 | -0.77 | -0.77 | -0.76 | -0.76 | -0.76 | -0.75 | -0.75 | -0.75 | -0.74 |
| 0.23 | -0.74 | -0.74 | -0.73 | -0.73 | -0.72 | -0.72 | -0.72 | -0.72 | -0.71 | -0.71 |
| 0.24 | -0.71 | -0.70 | -0.70 | -0.70 | -0.69 | -0.69 | -0.69 | -0.68 | -0.68 | -0.68 |
| 0.25 | -0.67 | -0.67 | -0.67 | -0.67 | -0.66 | -0.66 | -0.66 | -0.65 | -0.65 | -0.65 |
| 0.26 | -0.64 | -0.64 | -0.64 | -0.63 | -0.63 | -0.63 | -0.63 | -0.62 | -0.62 | -0.62 |
| 0.27 | -0.61 | -0.61 | -0.61 | -0.60 | -0.60 | -0.60 | -0.59 | -0.59 | -0.59 | -0.59 |
| 0.28 | -0.58 | -0.58 | -0.58 | -0.57 | -0.57 | -0.57 | -0.57 | -0.56 | -0.56 | -0.56 |
| 0.29 | -0.55 | -0.55 | -0.55 | -0.54 | -0.54 | -0.54 | -0.54 | -0.53 | -0.53 | -0.53 |
| 0.30 | -0.52 | -0.52 | -0.52 | -0.52 | -0.51 | -0.51 | -0.51 | -0.50 | -0.50 | -0.50 |
| 0.31 | -0.50 | -0.49 | -0.49 | -0.49 | -0.48 | -0.48 | -0.48 | -0.48 | -0.47 | -0.47 |
| 0.32 | -0.47 | -0.46 | -0.46 | -0.46 | -0.46 | -0.45 | -0.45 | -0.45 | -0.45 | -0.44 |
| 0.33 | -0.44 | -0.44 | -0.43 | -0.43 | -0.43 | -0.43 | -0.42 | -0.42 | -0.42 | -0.42 |
| 0.34 | -0.41 | -0.41 | -0.41 | -0.40 | -0.40 | -0.40 | -0.40 | -0.39 | -0.39 | -0.39 |
| 0.35 | -0.39 | -0.38 | -0.38 | -0.38 | -0.37 | -0.37 | -0.37 | -0.37 | -0.36 | -0.36 |
| 0.36 | -0.36 | -0.36 | -0..35 | -0.35 | -0.35 | -0.35 | -0.34 | -0.34 | -0.34 | -0.33 |
| 0.37 | -0.33 | -0.33 | -0.33 | -0.32 | -0.32 | -0.32 | -0.32 | -0.31 | -0.31 | -0.31 |
| 0.38 | -0.31 | -0.30 | -0.30 | -0.30 | -0.30 | -0.29 | -0.29 | -0.29 | -0.28 | -0.28 |
| 0.39 | -0.28 | -0.28 | -0.27 | -0.27 | -0.27 | -0.27 | -0.26 | -0.26 | -0.26 | -0.26 |
| 0.40 | -0.25 | -0.25 | -0.25 | -0.25 | -0.24 | -0.24 | -0.24 | -0.24 | -0.23 | -0.23 |
| 0.41 | -0.23 | -0.23 | -0.22 | -0.22 | -0.22 | -0.21 | -0.21 | -0.21 | -0.21 | -0.20 |
| 0.42 | -0.20 | -0.20 | -0.20 | -0.19 | -0.19 | -019 | -0.19 | -0.18 | -0.18 | -0.18 |
| 0.43 | -0.18 | -0.17 | -0.17 | -0.17 | -0.17 | -0.16 | -0.16 | -0.16 | -0.16 | -0.15 |
| 0.44 | -0.15 | -0.15 | -0.15 | -0.14 | -0.14 | -0.14 | -0.13 | -0.13 | -0.13 | -0.13 |
| 0.45 | -0.13 | -0.12 | -0.12 | -0.12 | -0.12 | -0.11 | -0.11 | -0.11 | -0.11 | -0.10 |
| 0.46 | -0.10 | -0.10 | -0.10 | -0.09 | -0.09 | -0.09 | -0.09 | -0.08 | -0.08 | -0.88 |
| 0.47 | -0.08 | -0.07 | -0.07 | -0.07 | -0.07 | -0.06 | -0.06 | -0.06 | -0.06 | -0.05 |
Продолжение таблицы 3
| a | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0.48 | -0.05 | -0.05 | -0.05 | -0.04 | -0.04 | -0.04 | -0.04 | -0.03 | -0.03 | -0.03 |
| 0.49 | -0.03 | -0.02 | -0.02 | -0.02 | -0.02 | -0.01 | -0.01 | -0.01 | -0.01 | -0.00 |
| 0.50 | 0.00 | 0.00 | 0.01 | 0.01 | 0.01 | 0.01 | 0.02 | 0.02 | 0.02 | 0.02 |
| 0.51 | 0.03 | 0.03 | 0.03 | 0.03 | 0.04 | 0.04 | 0.04 | 0.04 | 0.05 | 0.05 |
| 0.52 | 0.05 | 0.05 | 0.06 | 0.06 | 0.06 | 0.06 | 0.07 | 0.07 | 0.07 | 0.07 |
| 0.53 | 0.08 | 0.08 | 0.08 | 0.08 | 0.09 | 0.09 | 0.09 | 0.09 | 0.10 | 0.10 |
| 0.54 | 0.10 | 0.10 | 0.11 | 0.11 | 0.11 | 0.11 | 0.12 | 0.12 | 0.12 | 0.12 |
| 0.55 | 0.13 | 0.13 | 0.13 | 0.13 | 0.14 | 0.14 | 0.14 | 0.14 | 0.15 | 0.15 |
| 0.56 | 0.15 | 0.15 | 0.16 | 0.16 | 0.16 | 0.16 | 0.17 | 0.17 | 0.17 | 0.17 |
| 0.57 | 0.18 | 0.18 | 0.18 | 0.18 | 0.18 | 0.19 | 0.19 | 0.19 | 0.20 | 0.20 |
| 0.58 | 0.20 | 0.20 | 0.21 | 0.21 | 0.21 | 0.21 | 0.22 | 0.22 | 0.22 | 0.23 |
| 0.59 | 0.23 | 0.23 | 0.23 | 0.24 | 0.24 | 0.24 | 0.24 | 0.25 | 0.25 | 0.25 |
| 0.60 | 0.25 | 0.26 | 0.26 | 0.26 | 0.26 | 0.27 | 0.27 | 0.27 | 0.27 | 0.28 |
| 0.61 | 0.28 | 0.28 | 0.28 | 0.29 | 0.29 | 0.29 | 0.30 | 0.30 | 0.30 | 0.30 |
| 0.62 | 0.31 | 0.31 | 0.31 | 0.31 | 0.32 | 0.32 | 0.32 | 0.32 | 0.33 | 0.33 |
| 0.63 | 0.33 | 0.33 | 0.34 | 0.34 | 0.34 | 0.35 | 0.35 | 0.35 | 0.35 | 0.36 |
| 0.64 | 0.36 | 0.36 | 0.36 | 0.37 | 0.37 | 0.37 | 0.37 | 0.38 | 0.38 | 0.38 |
| 0.65 | 0.39 | 0.39 | 0.39 | 0.39 | 0.40 | 0.40 | 0.40 | 0.40 | 0.41 | 0.41 |
| 0.66 | 0.41 | 0.42 | 0.42 | 0.42 | 0.42 | 0.43 | 0.43 | 0.43 | 0.43 | 0.44 |
| 0.67 | 0.44 | 0.44 | 0.45 | 0.45 | 0.45 | 0.45 | 0.46 | 0.46 | 0.46 | 0.46 |
| 0.68 | 0.47 | 0.47 | 0.47 | 0.48 | 0.48 | 0.48 | 0.48 | 0.49 | 0.49 | 0.49 |
| 0.69 | 0.50 | 0.50 | 0.50 | 0.50 | 0.51 | 0.51 | 0.51 | 0.52 | 0.52 | 0.52 |
| 0.70 | 0.52 | 0.53 | 0.53 | 0.53 | 0.54 | 0.54 | 0.54 | 0.54 | 0.55 | 0.55 |
| 0.71 | 0.55 | 0.56 | 0.56 | 0.56 | 0.57 | 0.57 | 0.57 | 0.57 | 0.58 | 0.58 |
| 0.72 | 0.58 | 0.59 | 0.59 | 0.59 | 0.59 | 0.60 | 0.60 | 0.60 | 0.61 | 0.61 |
| 0.73 | 0.61 | 0.62 | 0.62 | 0.62 | 0.63 | 0.63 | 0.63 | 0.63 | 0.64 | 0.64 |
| 0.74 | 0.64 | 0.65 | 0.65 | 0.65 | 0.66 | 0.66 | 0.66 | 0.67 | 0.67 | 0.67 |
| 0.75 | 0.67 | 0.68 | 0.68 | 0.68 | 0.69 | 0.69 | 0.69 | 0.70 | 0.70 | 0.70 |
| 0.76 | 0.71 | 0.71 | 0.71 | 0.72 | 0.72 | 0.72 | 0.73 | 0.73 | 0.73 | 0.74 |
| 0.77 | 0.74 | 0.74 | 0.75 | 0.75 | 0.75 | 0.76 | 0.76 | 0.76 | 0.77 | 0.77 |
| 0.78 | 0.77 | 0.78 | 0.78 | 0.78 | 0.79 | 0.79 | 0.79 | 0.80 | 0.80 | 0.80 |
| 0.79 | 0.81 | 0.81 | 0.81 | 0.82 | 0.82 | 0.82 | 0.83 | 0.83 | 0.83 | 0.84 |
| 0.80 | 0.84 | 0.85 | 0.85 | 0.85 | 0.86 | 0.86 | 0.86 | 0.87 | 0.87 | 0.87 |
| 0.81 | 0.88 | 0.88 | 0.89 | 0.89 | 0.89 | 0.90 | 0.90 | 0.90 | 0.91 | 0.91 |
| 0.82 | 0.92 | 0.92 | 0.92 | 0.93 | 0.93 | 0.93 | 0.94 | 0.94 | 0.95 | 0.95 |
| 0.83 | 0.95 | 0.96 | 0.96 | 0.97 | 0.97 | 0.97 | 0.98 | 0.98 | 0.99 | 0.99 |
| 0.84 | 0.99 | 1.00 | 1.00 | 1.01 | 1.01 | 1.02 | 1.02 | 1.02 | 1.03 | 1.03 |
| 0.85 | 1.04 | 1.04 | 1.05 | 1.05 | 1.05 | 1.06 | 1.06 | 1.07 | 1.07 | 1.08 |
| 0.86 | 1.08 | 1.09 | 1.09 | 1.09 | 1.10 | 1.10 | 1.11 | 1.11 | 1.12 | 1.12 |
| 0.87 | 1.13 | 1.13 | 1.14 | 1.14 | 1.15 | 1.15 | 1.16 | 1.16 | 1.17 | 1.17 |
| 0.88 | 1.18 | 1.18 | 1.19 | 1.19 | 1.20 | 1.20 | 1.21 | 1.21 | 1.22 | 1.22 |
| 0.89 | 1.23 | 1.23 | 1.24 | 1.24 | 1.25 | 1.25 | 1.26 | 1.26 | 1.27 | 1.27 |
| 0.90 | 1.28 | 1.29 | 1.29 | 1.30 | 1.30 | 1.31 | 1.32 | 1.32 | 1.33 | 1.33 |
| 0.91 | 1.34 | 1.35 | 1.35 | 1.36 | 1.37 | 1.37 | 1.38 | 1.39 | 1.39 | 1.40 |
| 0.92 | 1.41 | 1.41 | 1.42 | 1.43 | 1.43 | 1.44 | 1.45 | 1.45 | 1.46 | 1.47 |
| 0.93 | 1.48 | 1.48 | 1.49 | 1.50 | 1.51 | 1.51 | 1.52 | 1.53 | 1.54 | 1.54 |
| 0.94 | 1.55 | 1.56 | 1.57 | 1.58 | 1.59 | 1.60 | 1.61 | 1.62 | 1.63 | 1.64 |
| 0.95 | 1.64 | 1.65 | 1.66 | 1.67 | 1.68 | 1.70 | 1.71 | 1.72 | 1.73 | 1.74 |
| 0.96 | 1.75 | 1.76 | 1.77 | 1.79 | 1.80 | 1.81 | 1.83 | 1.84 | 1.85 | 1.87 |
| 0.97 | 1.88 | 1.90 | 1.91 | 1.93 | 1.94 | 1.96 | 1.98 | 2.00 | 2.01 | 2.03 |
| 0.98 | 2.05 | 2.07 | 2.10 | 2.12 | 2.14 | 2.17 | 2.20 | 2.23 | 2.26 | 2.29 |
| 0.99 | 2.33 | 2.37 | 2.41 | 2.46 | 2.51 | 2.58 | 2.65 | 2.75 | 2.88 | 3.09 |
| α |
| f(Z) |
Таблица 4
Значения вероятности F(x) экспоненциального распределения 
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0.0 | 0, | - | 9900 | 9802 | 9704 | 9608 | 9512 | 9418 | 9324 | 9231 | 9139 |
| 0.1 | 0, | 9048 | 8958 | 8869 | 8781 | 8694 | 8607 | 8521 | 8437 | 8353 | 8270 |
| 0.2 | 0, | 8187 | 8106 | 8025 | 7945 | 7866 | 7788 | 7710 | 7634 | 7558 | 7483 |
| 0.3 | 0, | 7408 | 7334 | 7261 | 7189 | 7118 | 7047 | 6977 | 6907 | 6839 | 6771 |
| 0.4 | 0, | 6703 | 6636 | 6570 | 6505 | 6440 | 6376 | 6313 | 6250 | 6188 | 6126 |
| 0.5 | 0, | 6065 | 6005 | 5945 | 5886 | 5827 | 5770 | 5712 | 5655 | 5599 | 5543 |
| 0.6 | 0, | 5488 | 5433 | 5379 | 5325 | 5273 | 5220 | 5468 | 5117 | 5066 | 5016 |
| 0.7 | 0, | 4966 | 4916 | 4867 | 4819 | 4771 | 4724 | 4677 | 4630 | 4584 | 4538 |
| 0.8 | 0, | 4493 | 4449 | 4404 | 4360 | 4317 | 4274 | 4232 | 4189 | 4148 | 4107 |
| 0.9 | 0, | 4066 | 4025 | 3985 | 3945 | 3906 | 3867 | 3829 | 3791 | 3753 | 3716 |
| 1.0 | 0, | 3679 | 3642 | 3606 | 3570 | 3534 | 3499 | 3465 | 3430 | 3395 | 3362 |
| 1.1 | 0, | 3329 | 3296 | 3263 | 3230 | 3198 | 3166 | 3135 | 3104 | 3073 | 3042 |
| 1.2 | 0, | 3012 | 2982 | 2952 | 2923 | 2894 | 2865 | 2836 | 2808 | 2780 | 2753 |
| 1.3 | 0, | 2725 | 2698 | 2671 | 2645 | 2618 | 2592 | 2567 | 2541 | 2516 | 2491 |
| 1.4 | 0, | 2466 | 2441 | 2417 | 2393 | 2369 | 2346 | 2322 | 2299 | 2276 | 2254 |
| 1.5 | 0, | 2231 | 2209 | 2187 | 2165 | 2144 | 2122 | 2101 | 2080 | 2060 | 2039 |
| 1.6 | 0, | 2019 | 1999 | 1979 | 1959 | 1940 | 1920 | 1901 | 1882 | 1864 | 1845 |
| 1.7 | 0, | 1827 | 1809 | 1791 | 1773 | 1755 | 1738 | 1720 | 1703 | 1686 | 1670 |
| 1.8 | 0, | 1653 | 1636 | 1620 | 1604 | 1588 | 1572 | 1557 | 1541 | 1526 | 1511 |
| 1.9 | 0, | 1496 | 1481 | 1466 | 1451 | 1437 | 1423 | 1409 | 1395 | 1381 | 1367 |
| 2.0 | 0, | 1353 | 1340 | 1327 | 1313 | 1300 | 1287 | 1275 | 1262 | 1249 | 1237 |
| 2.1 | 0, | 1225 | 1212 | 1200 | 1188 | 1177 | 1165 | 1153 | 1142 | 1130 | 1119 |
| 2.2 | 0, | 1108 | 1097 | 1086 | 1075 | 1065 | 1054 | 1043 | 1033 | 1023 | 1013 |
| 2.3 | 0, | 1003 | 993 | 983 | 973 | 963 | 954 | 944 | 935 | 926 | 916 |
| 2.4 | 0,0 | 9072 | 8981 | 8892 | 8804 | 8716 | 8629 | 8544 | 8458 | 8374 | 8291 |
| 2.5 | 0,0 | 8208 | 8127 | 8046 | 7966 | 7887 | 7808 | 7730 | 7654 | 7577 | 7502 |
| 2.6 | 0,0 | 7427 | 7354 | 7280 | 7208 | 7136 | 7065 | 6995 | 6825 | 6856 | 6788 |
| 2.7 | 0,0 | 6721 | 6654 | 6581 | 6522 | 6457 | 6393 | 6329 | 6266 | 6204 | 6142 |
| 2.8 | 0,0 | 6081 | 6020 | 5961 | 4901 | 5843 | 5784 | 5727 | 5670 | 4514 | 5558 |
| 2.9 | 0,0 | 5502 | 5448 | 5393 | 5340 | 5287 | 5234 | 5182 | 5130 | 5079 | 5029 |
| 3.0 | 0,0 | 4979 | 4929 | 4880 | 4832 | 4784 | 4736 | 4689 | 4642 | 4596 | 4550 |
| 3.1 | 0,0 | 4505 | 4460 | 4416 | 4372 | 4328 | 4285 | 4243 | 4200 | 4159 | 4117 |
| 3.2 | 0,0 | 4076 | 4036 | 3995 | 3956 | 3916 | 3877 | 3839 | 3801 | 3163 | 3725 |
| 3.3 | 0,0 | 3688 | 3652 | 3615 | 3519 | 3544 | 3508 | 3474 | 3439 | 3405 | 3371 |
| 3.4 | 0,0 | 3337 | 3304 | 3271 | 3239 | 3206 | 3175 | 3143 | 3112 | 3081 | 3050 |
| 3.5 | 0,0 | 3020 | 2990 | 2960 | 2930 | 2901 | 2872 | 2844 | 2816 | 2788 | 2760 |
| 3.6 | 0,0 | 2732 | 2705 | 2578 | 2652 | 2625 | 2399 | 2573 | 2548 | 2522 | 2497 |
Таблица 4
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 3.7 | 0,0 | 2472 | 2448 | 2423 | 2399 | 2375 | 2352 | 2328 | 2305 | 2282 | 2260 |
| 3.8 | 0,0 | 2237 | 2215 | 2193 | 2171 | 2149 | 2128 | 2107 | 2086 | 2065 | 2044 |
| 3.9 | 0,0 | 2024 | 2004 | 1984 | 1964 | 1945 | 1925 | 1906 | 1887 | 1869 | 1850 |
| 4.0 | 0,0 | 1832 | 1813 | 1795 | 1777 | 1760 | 1742 | 1725 | 1708 | 1691 | 1674 |
| 4.1 | 0,0 | 1657 | 1641 | 1624 | 1608 | 1592 | 1576 | 1561 | 1545 | 1530 | 1515 |
| 4.2 | 0,0 | 1500 | 1485 | 1470 | 1455 | 1441 | 1426 | 1412 | 1398 | 1384 | 1370 |
| 4.3 | 0,0 | 1357 | 1343 | 1330 | 1317 | 1304 | 1291 | 1278 | 1265 | 1253 | 1241 |
| 4.4 | 0,0 | 1228 | 1216 | 1203 | 1191 | 1180 | 1168 | 1156 | 1145 | 1133 | 1122 |
| 4.5 | 0,0 | 1111 | 1100 | 1089 | 1078 | 1067 | 1057 | 1046 | 1035 | 1025 | 1015 |
| 4.6 | 0,0 | 1005 | 995 | 985 | 975 | 966 | 956 | 947 | 937 | 928 | 919 |
| 4.7 | 0,00 | 9095 | 9005 | 8915 | 8826 | 8739 | 8652 | 8566 | 8480 | 8356 | 8312 |
| 4.8 | 0,00 | 8230 | 8148 | 8067 | 7985 | 7907 | 7828 | 7760 | 7573 | 7897 | 7521 |
| 4.9 | 0,00 | 7447 | 7372 | 7299 | 7226 | 7155 | 7083 | 7013 | 6943 | 6874 | 6806 |
| 5.0 | 0,00 | 6738 | 6671 | 6604 | 6639 | 6474 | 6409 | 6346 | 6282 | 6220 | 6158 |
| x | a | b | x | a | b | x | a | b | x | a | b |
| 1.0 | 3.679 | 1 | 6 | 2.479 | 3 | 20 | 2.061 | 9 | 70 | 3.975 | 31 |
| 2.0 | 1.353 | 1 | 7 | 9.119 | 4 | 30 | 9.358 | 14 | 80 | 1.805 | 35 |
| 3.0 | 4.979 | 2 | 8 | 3.355 | 4 | 40 | 4.248 | 18 | 90 | 8.194 | 40 |
| 4.0 | 1.832 | 2 | 9 | 1.234 | 4 | 50 | 1.929 | 22 | 100 | 3.72 | 44 |
| 5.0 | 6.738 | 3 | 10 | 4.54 | 5 | 60 | 8.757 | 27 |
Таблица 5
Значения натуральных логарифмов 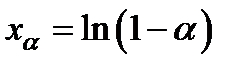
|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0.01 | 4.6052 | 4.5099 | 4.4229 | 4.3428 | 4.2687 | 4.1997 | 4.1352 | 4.0746 | 4.0174 | 3.9633 | |
| 0.02 | 3.9120 | 3.8633 | 3.8167 | 3.7623 | 3.7297 | 3.6889 | 3.6497 | 3.6019 | 3.5756 | 3.5305 | |
| 0.03 | 3.5066 | 3.4638 | 3.5970 | 3.4013 | 3.3714 | 3.3444 | 3.3143 | 3.2969 | 3.2602 | 2.2342 | |
| 0.04 | 3.2189 | 3.1942 | 3.1701 | 3.1501 | 3.2136 | 3.1011 | 3.0791 | 3.0576 | 3.0366 | 3.016 | |
| 0.05 | 2.9957 | 2.976 | 2.9565 | 2.9375 | 2.9188 | 2.9005 | 2.8824 | 2.8647 | 2.8473 | 2.8202 | |
| 0.06 | 2.8134 | 2.7968 | 2.7807 | 2.7647 | 2.7489 | 2.7334 | 2.7181 | 2.7031 | 2.6883 | 2.6737 | |
| 0.07 | 2.6593 | 2.6451 | 2.6301 | 2.6173 | 2.6037 | 2.5903 | 2.5771 | 2.5640 | 2.5501 | 2.5383 | |
| 0.08 | 2.5257 | 2.5133 | 2.5011 | 2.4189 | 2.4770 | 2.4651 | 2.4434 | 2.4419 | 2.4304 | 2.4191 | |
| 0.09 | 2.4079 | 2.3969 | 2.3860 | 2.3652 | 2.3645 | 2.3539 | 2.3434 | 2.3331 | 2.3228 | 2.3127 | |
| 0.1 | 2.3026 | 2.2073 | 2.2103 | 2.0402 | 1.9661 | 1.8971 | 1.8326 | 1.7720 | 1.7148 | 1.6607 | |
| 0.2 | 1.6094 | 1.5601 | 1.5141 | 1.4697 | 1.4271 | 1.3863 | 1.3471 | 1.3093 | 1.2730 | 1.2379 | |
| 0.3 | 1.2040 | 1.1712 | 1.1394 | 1.1077 | 1.0788 | 1.0498 | 1.0217 | 0.9943 | 0.9676 | 0.9416 | |
| 0.4 | 0.9163 | 0.8916 | 0.8775 | 0.8440 | 0.8210 | 0.7985 | 0.7765 | 0.7550 | 0.7340 | 0.7134 | |
| 0.5 | 0.6931 | 0.6734 | 0.6539 | 0.6349 | 0.6162 | 0.5979 | 0.5798 | 0.5621 | 0.5447 | 0.5276 | |
| 0.6 | 0.5108 | 0.4943 | 0.4781 | 0.4521 | 0.4413 | 0.4208 | 0.4155 | 0.4005 | 0.3857 | 0.3711 | |
| 0.7 | 0.3567 | 0.3425 | 0.3285 | 0.3147 | 0.3011 | 0.2877 | 0.2745 | 0.2614 | 0.2485 | 0.2357 | |
| 0.8 | 0.2231 | 0.2107 | 0.1985 | 0.1863 | 0.1744 | 0.1625 | 0.1508 | 0.1393 | 0.1278 | 0.1165 | |
| 0.9 | 0.1054 | 0.0943 | 0.0834 | 0.0726 | 0.0619 | 0.0513 | 0.0408 | 0.0305 | 0.0202 | 0.0101 | |
| 0.91 | 0.0943 | 0.0932 | 0.0921 | 0.0910 | 0.0899 | 0.0888 | 0.0877 | 0.0866 | 0.0856 | 0.0845 | |
| 0.92 | 0.0834 | 0.0823 | 0.0812 | 0.0801 | 0.0790 | 0.0780 | 0.0769 | 0.0758 | 0.0747 | 0.0736 | |
| 0.93 | 0.0726 | 0.0715 | 0.0704 | 0.0694 | 0.0683 | 0.0672 | 0.0661 | 0.0651 | 0.0640 | 0.0629 | |
| 0.94 | 0.0619 | 0.0608 | 0.0598 | 0.0587 | 0.0576 | 0.0566 | 0.0555 | 0.0545 | 0.0534 | 0.0523 | |
| 0.95 | 0.0513 | 0.0503 | 0.0492 | 0.0481 | 0.0471 | 0.0460 | 0.0450 | 0.0440 | 0.0429 | 0.0419 | |
| 0.96 | 0.0408 | 0.0398 | 0.0387 | 0.0377 | 0.0367 | 0.0356 | 0.0346 | 0.0336 | 0.0325 | 0.0315 | |
| 0.97 | 0.0305 | 0.0294 | 0.0284 | 0.0274 | 0.0263 | 0.0253 | 0.0243 | 0.0233 | 0.0222 | 0.0212 | |
| 0.98 | 0.0202 | 0.0192 | 0.0182 | 0.0171 | 0.0161 | 0.0151 | 0.0141 | 0.0131 | 0.0121 | 0.0111 | |
| 0.99 | 0.0101 | 0.0091 | 0.0080 | 0.0070 | 0.0060 | 0.0050 | 0.0040 | 0.0030 | 0.0020 | 0.0010 | |
Таблица 6
| P m P m |
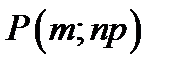 биномиального распределения
биномиального распределения 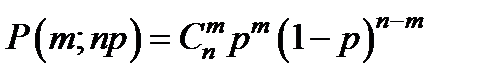
| n | 0.01 | 0.02 | 0.04 | 0.06 | 0.08 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | |||
| 5 | 0 | 0.95099 | 0.90392 | 0.81537 | 0.73390 | 0.65908 | 0.59049 | 0.32768 | 0.16807 | 0.07776 | 0.03125 | 5 | 5 |
| 1 | 0.04803 | 0.09224 | 0.16987 | 0.23422 | 0.28656 | 0.32805 | 0.40960 | 0.36015 | 0.25920 | 0.15625 | 4 | ||
| 2 | 0.00097 | 0.00376 | 0.01416 | 0.02990 | 0.04984 | 0.07290 | 0.20480 | 0.30870 | 0.34560 | 0.31250 | 3 | ||
| 3 | 0.00001 | 0.00008 | 0.00059 | 0.00191 | 0.00433 | 0.00810 | 0.05120 | 0.13230 | 0.23040 | 0.31250 | 2 | ||
| 4 | 0.00001 | 0.00006 | 0.00019 | 0.00045 | 0.00640 | 0.02835 | 0.07680 | 0.15625 | 1 | ||||
| 5 | 0.00001 | 0.00032 | 0.00243 | 0.01024 | 0.03125 | 0 | |||||||
| 10 | 0 | 0.90438 | 0.81707 | 0.66483 | 0.53862 | 0.43439 | 0.34868 | 0.10737 | 0.02825 | 0.00605 | 0.00098 | 10 | 10 |
| 1 | 0.09135 | 0.16675 | 0.27701 | 0.34380 | 0.37773 | 0.38742 | 0.26844 | 0.12106 | 0.04031 | 0.00977 | 9 | ||
| 2 | 0.00415 | 0.01531 | 0.05194 | 0.09875 | 0.14781 | 0.19371 | 0.30199 | 0.23347 | 0.12093 | 0.04395 | 8 | ||
| 3 | 0.00011 | 0.00083 | 0.00577 | 0.01681 | 0.03427 | 0.05740 | 0.20133 | 0.26683 | 0.21499 | 0.11719 | 7 | ||
| 4 | 0.00003 | 0.00042 | 0.00188 | 0.00522 | 0.01116 | 0.08808 | 0.20012 | 0.25082 | 0.20508 | 6 | |||
| 5 | 0.00002 | 0.00014 | 0.00054 | 0.00149 | 0.02642 | 0.10292 | 0.20066 | 0.24609 | 5 | ||||
| 6 | 0.00001 | 0.00004 | 0.00014 | 0.00551 | 0.03676 | 0.11148 | 0.20508 | 4 | |||||
| 7 | 0.00001 | 0.00079 | 0.00900 | 0.04247 | 0.11719 | 3 | |||||||
| 8 | 0.00007 | 0.00145 | 0.01062 | 0.04395 | 2 | ||||||||
| 9 | 0.00014 | 0.00157 | 0.00977 | 1 | |||||||||
| 10 | 0.00001 | 0.00010 | 0.00098 | 0 | |||||||||
| 15 | 0 | 0.86006 | 0.73857 | 0.54209 | 0.39529 | 0.28630 | 0.20589 | 0.03518 | 0.00475 | 0.00047 | 0.00003 | 15 | 15 |
| 1 | 0.13031 | 0.22609 | 0.33880 | 0.37847 | 0.37343 | 0.34315 | 0.13194 | 0.03052 | 0.00470 | 0.00046 | 14 | ||
| 2 | 0.00921 | 0.03230 | 0.09882 | 0.16910 | 0.22731 | 0.26690 | 0.23090 | 0.09156 | 0.02194 | 0.00320 | 13 | ||
| 3 | 0.00040 | 0.00286 | 0.01784 | 0.04677 | 0.08565 | 0.12851 | 0.25014 | 0.17004 | 0.06339 | 0.01389 | 12 | ||
| 4 | 0.00001 | 0.00017 | 0.00223 | 0.00896 | 0.02234 | 0.04284 | 0.18760 | 0.21862 | 0.12678 | 0.04166 | 11 | ||
| 5 | 0.00001 | 0.00020 | 0.00126 | 0.00427 | 0.01047 | 0.10318 | 0.20613 | 0.18594 | 0.09164 | 10 | |||
| 6 | 0.00001 | 0.00013 | 0.00062 | 0.00194 | 0.04299 | 0.14724 | 0.20660 | 0.15274 | 9 | ||||
| 7 | 0.00001 | 0.00007 | 0.00028 | 0.01382 | 0.08113 | 0.17708 | 0.19638 | 8 | |||||
| 8 | 0.00001 | 0.00003 | 0.00345 | 0.03477 | 0.11806 | 0.19638 | 7 | ||||||
| 9 | 0.00067 | 0.01159 | 0.06121 | 0.15274 | 6 | ||||||||
| 10 | 0.00010 | 0.00298 | 0.02449 | 0.09164 | 5 | ||||||||
| 11 | 0.00001 | 0.00058 | 0.00742 | 0.04166 | 4 | ||||||||
| 12 | 0.00008 | 0.00165 | 0.01389 | 3 | |||||||||
| 13 | 0.00001 | 0.00025 | 0.00320 | 2 | |||||||||
| 14 | 0.00002 | 0.00046 | 1 | ||||||||||
| 15 | 0.00003 | 0 | |||||||||||
| 20 | 0 | 0.81791 | 0.66761 | 0.44200 | 0.29011 | 0.18869 | 0.12158 | 0.01153 | 0.00080 | 0.00004 | 20 | 20 | |
| 1 | 0.16523 | 0.27249 | 0.36834 | 0.37035 | 0.32816 | 0.27017 | 0.05765 | 0.00684 | 0.00049 | 0.00002 | 19 | ||
| 2 | 0.01586 | 0.05283 | 0.14580 | 0.22457 | 0.27109 | 0.28518 | 0.13691 | 0.02785 | 0.00309 | 0.00018 | 18 | ||
| 3 | 0.00096 | 0.00647 | 0.03645 | 0.08601 | 0.14144 | 0.19012 | 0.20536 | 0.07160 | 0.01235 | 0.00109 | 17 | ||
| 4 | 0.00004 | 0.00056 | 0.00645 | 0.02333 | 0.05227 | 0.08978 | 0.21820 | 0.13042 | 0.03499 | 0.00462 | 16 | ||
| 5 | 0.00004 | 0.00086 | 0.00477 | 0.01454 | 0.03192 | 0.17456 | 0.17886 | 0.07465 | 0.01479 | 15 | |||
| 6 | 0.00009 | 0.00076 | 0.00316 | 0.00887 | 0.10910 | 0.19164 | 0.12441 | 0.03696 | 14 | ||||
| 7 | 0.00001 | 0.00010 | 0.00055 | 0.00197 | 0.05455 | 0.16426 | 0.16588 | 0.07393 | 13 | ||||
| 8 | 0.00001 | 0.00008 | 0.00036 | 0.02216 | 0.11440 | 0.17971 | 0.12013 | 12 | |||||
| 9 | 0.00001 | 0.00005 | 0.00739 | 0.06537 | 0.15974 | 0.16018 | 11 | ||||||
| 10 | 0.00001 | 0.00203 | 0.03082 | 0.11714 | 0.17620 | 10 | |||||||
| 11 | 0.00046 | 0.01201 | 0.07099 | 0.16018 | 9 | ||||||||
| 12 | 0.00009 | 0.00386 | 0.03550 | 0.12013 | 8 | ||||||||
| 13 | 0.00001 | 0.00102 | 0.01456 | 0.07393 | 7 | ||||||||
| 14 | 0.00022 | 0.00485 | 0.03696 | 6 | |||||||||
| 15 | 0.00004 | 0.00129 | 0.01479 | 5 | |||||||||
| 16 | 0.00001 | 0.00027 | 0.00462 | 4 | |||||||||
| 17 | 0.00004 | 0.00109 | 3 | ||||||||||
| 18 | 0.00018 | 2 | |||||||||||
| 19 | 0.00002 | 1 | |||||||||||
| 20 |
| 0 | |||||||||||
| 0.99 | 0.98 | 0.96 | 0.94 | 0.92 | 0.9 | 0.8 | 0.7 | 0.6 | 0.5 | n |
продолжение табл. 6
| n |
P m | 0.01 | 0.02 | 0.04 | 0.06 | 0.08 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 |
| |
| 25 | 0 | 0.77782 | 0.60346 | 0.36040 | 0.21291 | 0.12436 | 0.07179 | 0.00378 | 0.00013 | 0.00000 | 0.00000 | 25 | 25 |
| 1 | 0.19642 | 0.30789 | 0.37541 | 0.33975 | 0.27036 | 0.19942 | 0.02361 | 0.00144 | 0.00005 | 0.00000 | 24 | ||
| 2 | 0.02381 | 0.07540 | 0.18771 | 0.26023 | 0.28211 | 0.26589 | 0.07084 | 0.00739 | 0.00038 | 0.00001 | 23 | ||
| 3 | 0.00184 | 0.01180 | 0.05996 | 0.12735 | 0.18807 | 0.22650 | 0.13577 | 0.02428 | 0.00194 | 0.00007 | 22 | ||
| 4 | 0.00010 | 0.00132 | 0.01374 | 0.04471 | 0.08995 | 0.13842 | 0.18668 | 0.05723 | 0.00710 | 0.00038 | 21 | ||
| 5 | 0.00011 | 0.00240 | 0.01199 | 0.03285 | 0.06459 | 0.19602 | 0.10302 | 0.01989 | 0.00158 | 20 | |||
| 6 | 0.00001 | 0.00033 | 0.00255 | 0.00952 | 0.02392 | 0.16335 | 0.14717 | 0.04420 | 0.00528 | 19 | |||
| 7 | 0.00004 | 0.00044 | 0.00225 | 0.00722 | 0.11084 | 0.17119 | 0.07999 | 0.01433 | 18 | ||||
| 8 | 0.00006 | 0.00044 | 0.00180 | 0.06235 | 0.16508 | 0.11998 | 0.03223 | 17 | |||||
| 9 | 0.00001 | 0.00007 | 0.00038 | 0.02944 | 0.13364 | 0.15109 | 0.06089 | 16 | |||||
| 10 | 0.00001 | 0.00007 | 0.01178 | 0.09164 | 0.16116 | 0.09742 | 15 | ||||||
| 11 | 0.00001 | 0.00401 | 0.05355 | 0.14651 | 0.13284 | 14 | |||||||
| 12 | 0.00117 | 0.02678 | 0.11395 | 0.15498 | 13 | ||||||||
| 13 | 0.00029 | 0.01148 | 0.07597 | 0.15498 | 12 | ||||||||
| 14 | 0.00006 | 0.00422 | 0.04341 | 0.13284 | 11 | ||||||||
| 15 | 0.00001 | 0.00132 | 0.02122 | 0.09742 | 10 | ||||||||
| 16 | 0.00035 | 0.00884 | 0.06089 | 9 | |||||||||
| 17 | 0.00008 | 0.00312 | 0.03223 | 8 | |||||||||
| 18 | 0.00002 | 0.00092 | 0.01433 | 7 | |||||||||
| 19 | 0.00023 | 0.00528 | 6 | ||||||||||
| 20 | 0.00005 | 0.00158 | 5 | ||||||||||
| 21 | 0.00001 | 0.00038 | 4 | ||||||||||
| 22 | 0.00007 | 3 | |||||||||||
| 23 | 0.00001 | 2 | |||||||||||
| 30 | 0 | 0.73970 | 0.54548 | 0.29386 | 0.15626 | 0.08197 | 0.04239 | 0.00124 | 0.00002 | 30 | 30 | ||
| 1 | 0.22415 | 0.33397 | 0.36732 | 0.29921 | 0.21382 | 0.14130 | 0.00928 | 0.00029 | 29 | ||||
| 2 | 0.03283 | 0.09883 | 0.22192 | 0.27693 | 0.26961 | 0.22766 | 0.03366 | 0.00180 | 0.00004 | 28 | |||
| 3 | 0.00310 | 0.01882 | 0.08630 | 0.16498 | 0.21881 | 0.23609 | 0.07853 | 0.00720 | 0.00027 | 27 | |||
| 4 | 0.00021 | 0.00259 | 0.02427 | 0.07108 | 0.12843 | 0.17707 | 0.13252 | 0.02084 | 0.00120 | 0.00003 | 26 | ||
| 5 | 0.00001 | 0.00028 | 0.00526 | 0.02359 | 0.05807 | 0.10230 | 0.17228 | 0.04644 | 0.00415 | 0.00013 | 25 | ||
| 6 | 0.00002 | 0.00091 | 0.00627 | 0.02104 | 0.04736 | 0.17946 | 0.08293 | 0.01152 | 0.00055 | 24 | |||
| 7 | 0.00013 | 0.00137 | 0.00627 | 0.01804 | 0.15382 | 0.12185 | 0.02634 | 0.00190 | 23 | ||||
| 8 | 0.00002 | 0.00025 | 0.00157 | 0.00576 | 0.11056 | 0.15014 | 0.05049 | 0.00545 | 22 | ||||
| 9 | 0.00004 | 0.00033 | 0.00157 | 0.06756 | 0.15729 | 0.08228 | 0.01332 | 21 | |||||
| 10 | 0.00001 | 0.00006 | 0.00037 | 0.03547 | 0.14156 | 0.11519 | 0.02798 | 20 | |||||
| 11 | 0.00001 | 0.00007 | 0.01612 | 0.11031 | 0.13962 | 0.05088 | 19 | ||||||
| 12 | 0.00001 | 0.00638 | 0.07485 | 0.14738 | 0.08055 | 18 | |||||||
| 13 | 0.00221 | 0.04442 | 0.13604 | 0.11154 | 17 | ||||||||
| 14 | 0.00067 | 0.02312 | 0.11013 | 0.13544 | 16 | ||||||||
| 15 | 0.00018 | 0.01057 | 0.07831 | 0.14446 | 15 | ||||||||
| 16 | 0.00004 | 0.00425 | 0.04895 | 0.13544 | 14 | ||||||||
| 17 | 0.00001 | 0.00150 | 0.02687 | 0.11154 | 13 | ||||||||
| 18 | 0.00046 | 0.01294 | 0.08055 | 12 | |||||||||
| 19 | 0.00013 | 0.00545 | 0.05088 | 11 | |||||||||
| 20 | 0.00003 | 0.00200 | 0.02798 | 10 | |||||||||
| 21 | 0.00001 | 0.00063 | 0.01332 | 9 | |||||||||
| 22 | 0.00017 | 0.00545 | 8 | ||||||||||
| 23 | 0.00004 | 0.00190 | 7 | ||||||||||
| 24 | 0.00001 | 0.00055 | 6 | ||||||||||
| 25 | 0.00013 | 5 | |||||||||||
| 26 | 0.00003 | 4 | |||||||||||
|
| 0.99 | 0.98 | 0.96 | 0.94 | 0.92 | 0.9 | 0.8 | 0.7 | 0.6 | 0.5 | n |
Таблица 7
Значения функции F(t)=α распределения Стьюдента 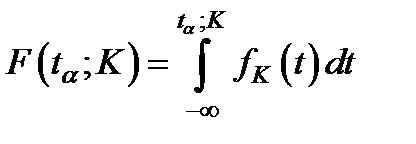
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 0.0 | 0.50000 | 0.50000 | 0.50000 | 0.50000 | 0.50000 | 0.50000 | 0.50000 | 0.50000 | 0.50000 | 0.50000 | |
| 0.1 | 0.53173 | 0.53527 | 0.53667 | 0.53742 | 0.53788 | 0.53820 | 0.53843 | 0.53860 | 0.53873 | 0.53884 | |
| 0.2 | 0.56283 | 0.57001 | 0.57286 | 0.57438 | 0.57532 | 0.57596 | 0.57642 | 0.57676 | 0.57704 | 0.57726 | |
| 0.3 | 0.59277 | 0.60376 | 0.60812 | 0.61044 | 0.61188 | 0.61285 | 0.61355 | 0.61409 | 0.61450 | 0.61484 | |
| 0.4 | 0.62112 | 0.63608 | 0.64203 | 0.64520 | 0.64716 | 0.64850 | 0.64946 | 0.65019 | 0.65076 | 0.65122 | |
| 0.5 | 0.64758 | 0.66667 | 0.67428 | 0.67834 | 0.68085 | 0.68256 | 0.68380 | 0.68473 | 0.68546 | 0.68605 | |
| 0.6 | 0.67202 | 0.69528 | 0.70460 | 0.70958 | 0.71267 | 0.71477 | 0.71629 | 0.71744 | 0.71835 | 0.71907 | |
| 0.7 | 0.69440 | 0.72180 | 0.73284 | 0.73875 | 0.74243 | 0.74493 | 0.74674 | 0.74811 | 0.74919 | 0.75006 | |
| 0.8 | 0.71478 | 0.74618 | 0.75890 | 0.76574 | 0.76999 | 0.77289 | 0.77500 | 0.77659 | 0.77784 | 0.77885 | |
| 0.9 | 0.73326 | 0.76845 | 0.78277 | 0.79050 | 0.79531 | 0.79860 | 0.80099 | 0.80280 | 0.80422 | 0.80536 | |
| 1.0 | 0.75000 | 0.78868 | 0.80450 | 0.81305 | 0.81839 | 0.82204 | 0.82469 | 0.82670 | 0.82828 | 0.82955 | |
| 1.1 | 0.76515 | 0.80698 | 0.82416 | 0.83346 | 0.83927 | 0.84325 | 0.84614 | 0.84834 | 0.85006 | 0.85145 | |
| 1.2 | 0.77886 | 0.82350 | 0.84187 | 0.85182 | 0.85805 | 0.86232 | 0.86541 | 0.86777 | 0.86961 | 0.87110 | |
| 1.3 | 0.79129 | 0.83838 | 0.85777 | 0.86827 | 0.87485 | 0.87935 | 0.88262 | 0.88510 | 0.88705 | 0.88862 | |
| 1.4 | 0.80257 | 0.85176 | 0.87200 | 0.88295 | 0.88980 | 0.89448 | 0.89788 | 0.90046 | 0.90249 | 0.90412 | |
| 1.5 | 0.81283 | 0.86380 | 0.88471 | 0.89600 | 0.90305 | 0.90786 | 0.91135 | 0.91400 | 0.91607 | 0.91775 | |
| 1.6 | 0.82219 | 0.87463 | 0.89605 | 0.90758 | 0.91475 | 0.91964 | 0.92318 | 0.92587 | 0.92797 | 0.92966 | |
| 1.7 | 0.83075 | 0.88438 | 0.90615 | 0.91782 | 0.92506 | 0.92998 | 0.93354 | 0.93622 | 0.93833 | 0.94002 | |
| 1.8 | 0.83859 | 0.89317 | 0.91516 | 0.92688 | 0.93412 | 0.93902 | 0.94256 | 0.94522 | 0.94730 | 0.94897 | |
| 1.9 | 0.84579 | 0.90109 | 0.92318 | 0.93488 | 0.94207 | 0.94692 | 0.95040 | 0.95302 | 0.95506 | 0.95669 | |
| 2.0 | 0.85242 | 0.90825 | 0.93034 | 0.94194 | 0.94903 | 0.95379 | 0.95719 | 0.95974 | 0.96172 | 0.96331 | |
| 2.1 | 0.85854 | 0.91473 | 0.93672 | 0.94817 | 0.95512 | 0.95976 | 0.96306 | 0.96553 | 0.96744 | 0.96896 | |
| 2.2 | 0.86420 | 0.92060 | 0.94241 | 0.95367 | 0.96045 | 0.96495 | 0.96813 | 0.97050 | 0.97233 | 0.97378 | |
| 2.3 | 0.86945 | 0.92593 | 0.94751 | 0.95853 | 0.96511 | 0.96945 | 0.97250 | 0.97476 | 0.97650 | 0.97787 | |
| 2.4 | 0.87433 | 0.93077 | 0.95206 | 0.96282 | 0.96919 | 0.97335 | 0.97627 | 0.97841 | 0.98005 | 0.98134 | |
| 2.5 | 0.87888 | 0.93519 | 0.95615 | 0.96662 | 0.97275 | 0.97674 | 0.97950 | 0.98153 | 0.98307 | 0.98428 | |
| 2.6 | 0.88312 | 0.93923 | 0.95981 | 0.96998 | 0.97588 | 0.97967 | 0.98229 | 0.98419 | 0.98563 | 0.98675 | |
| 2.7 | 0.88709 | 0.94292 | 0.96311 | 0.97295 | 0.97861 | 0.98221 | 0.98468 | 0.98646 | 0.98780 | 0.98884 | |
| 2.8 | 0.89081 | 0.94630 | 0.96607 | 0.97559 | 0.98100 | 0.98442 | 0.98674 | 0.98840 | 0.98964 | 0.99060 | |
| 2.9 | 0.89430 | 0.94941 | 0.96875 | 0.97794 | 0.98310 | 0.98633 | 0.98851 | 0.99005 | 0.99120 | 0.99208 | |
| 3.0 | 0.89758 | 0.95227 | 0.97117 | 0.98003 | 0.98495 | 0.98800 | 0.99003 | 0.99146 | 0.99252 | 0.99333 | |
| 3.1 | 0.90067 | 0.95490 | 0.97335 | 0.98189 | 0.98657 | 0.98944 | 0.99134 | 0.99267 | 0.99364 | 0.99437 | |
| 3.2 | 0.90359 | 0.95733 | 0.97533 | 0.98355 | 0.98800 | 0.99070 | 0.99247 | 0.99369 | 0.99458 | 0.99525 | |
| 3.3 | 0.90634 | 0.95958 | 0.97713 | 0.98503 | 0.98926 | 0.99180 | 0.99344 | 0.99457 | 0.99539 | 0.99599 | |
| 3.4 | 0.90895 | 0.96166 | 0.97877 | 0.98636 | 0.99037 | 0.99275 | 0.99428 | 0.99532 | 0.99606 | 0.99661 | |
| 3.5 | 0.91141 | 0.96359 | 0.98026 | 0.98755 | 0.99136 | 0.99359 | 0.99500 | 0.99596 | 0.99664 | 0.99714 | |
| 3.6 | 0.91375 | 0.96538 | 0.98162 | 0.98862 | 0.99223 | 0.99432 | 0.99563 | 0.99651 | 0.99713 | 0.99758 | |
| 3.7 | 0.91598 | 0.96705 | 0.98286 | 0.98958 | 0.99300 | 0.99496 | 0.99617 | 0.99698 | 0.99754 | 0.99795 | |
| 3.8 | 0.91809 | 0.96860 | 0.98400 | 0.99045 | 0.99369 | 0.99552 | 0.99664 | 0.99738 | 0.99789 | 0.99826 | |
| 3.9 | 0.92010 | 0.97005 | 0.98504 | 0.99123 | 0.99430 | 0.99601 | 0.99705 | 0.99773 | 0.99819 | 0.99852 | |
| 4.0 | 0.92202 | 0.97140 | 0.98600 | 0.99193 | 0.99484 | 0.99644 | 0.99741 | 0.99803 | 0.99844 | 0.99874 | |
| 4.2 | 0.92560 | 0.97386 | 0.98768 | 0.99315 | 0.99576 | 0.99716 | 0.99798 | 0.99850 | 0.99885 | 0.99909 | |
| 4.4 | 0.92887 | 0.97602 | 0.98912 | 0.99415 | 0.99649 | 0.99772 | 0.99842 | 0.99886 | 0.99914 | 0.99933 | |
| 4.6 | 0.93186 | 0.97792 | 0.99034 | 0.99498 | 0.99708 | 0.99815 | 0.99876 | 0.99912 | 0.99935 | 0.99951 | |
| 4.8 | 0.93462 | 0.97962 | 0.99140 | 0.99568 | 0.99756 | 0.99850 | 0.99902 | 0.99932 | 0.99951 | 0.99964 | |
| 5.0 | 0.93717 | 0.98113 | 0.99230 | 0.99625 | 0.99795 | 0.99877 | 0.99922 | 0.99947 | 0.99963 | 0.99973 | |
| 5.2 | 0.93952 | 0.98248 | 0.99309 | 0.99674 | 0.99827 | 0.99899 | 0.99937 | 0.99959 | 0.99972 | 0.99980 | |
| 5.4 | 0.94171 | 0.98369 | 0.99378 | 0.99715 | 0.99853 | 0.99917 | 0.99950 | 0.99968 | 0.99978 | 0.99985 | |
| 5.6 | 0.94375 | 0.98478 | 0.99437 | 0.99750 | 0.99875 | 0.99931 | 0.99959 | 0.99974 | 0.99983 | 0.99989 | |
| 5.8 | 0.94565 | 0.98577 | 0.99490 | 0.99780 | 0.99893 | 0.99942 | 0.99967 | 0.99980 | 0.99987 | 0.99991 | |
| 6.0 | 0.94743 | 0.98666 | 0.99536 | 0.99806 | 0.99908 | 0.99952 | 0.99973 | 0.99984 | 0.99990 | 0.99993 | |
| 6.2 | 0.94910 | 0.98748 | 0.99577 | 0.99828 | 0.99920 | 0.99959 | 0.99978 | 0.99987 | 0.99992 | 0.99995 | |
| 6.4 | 0.95066 | 0.98822 | 0.99614 | 0.99847 | 0.99931 | 0.99966 | 0.99982 | 0.99990 | 0.99994 | 0.99996 | |
| 6.6 | 0.95214 | 0.98890 | 0.99646 | 0.99863 | 0.99940 | 0.99971 | 0.99985 | 0.99992 | 0.99995 | 0.99997 | |
| 6.8 | 0.95352 | 0.98953 | 0.99675 | 0.99878 | 0.99948 | 0.99975 | 0.99987 | 0.99993 | 0.99996 | 0.99998 | |
| 7.0 | 0.95483 | 0.99010 | 0.99701 | 0.99890 | 0.99954 | 0.99979 | 0.99989 | 0.99994 | 0.99997 | 0.99998 | |
| 7.2 | 0.95607 | 0.99063 | 0.99724 | 0.99901 | 0.99960 | 0.99982 | 0.99991 | 0.99995 | 0.99997 | 0.99999 | |
| 7.4 | 0.95724 | 0.99111 | 0.99745 | 0.99911 | 0.99965 | 0.99984 | 0.99993 | 0.99996 | 0.99998 | 0.99999 | |
| 7.6 | 0.95836 | 0.99156 | 0.99764 | 0.99920 | 0.99969 | 0.99986 | 0.99994 | 0.99997 | 0.99998 | 0.99999 | |
| 7.8 | 0.95941 | 0.99198 | 0.99781 | 0.99927 | 0.99972 | 0.99988 | 0.99995 | 0.99997 | 0.99999 | 0.99999 | |
| 8.0 | 0.96042 | 0.99237 | 0.99796 | 0.99934 | 0.99975 | 0.99990 | 0.99995 | 0.99998 | 0.99999 | 0.99999 |
Продолжение таблицы 7
| K t |
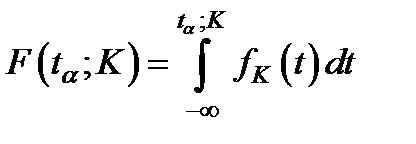
|
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 0.0 | 0.50000 | 0.50000 | 0.50000 | 0.50000 | 0.50000 | 0.50000 | 0.50000 | 0.50000 | 0.50000 | 0.50000 |
| 0.1 | 0.53893 | 0.53900 | 0.53906 | 0.53912 | 0.53917 | 0.53921 | 0.53924 | 0.53928 | 0.53930 | 0.53933 |
| 0.2 | 0.57743 | 0.57759 | 0.57771 | 0.57782 | 0.57792 | 0.57800 | 0.57807 | 0.57814 | 0.57820 | 0.57825 |
| 0.3 | 0.61511 | 0.61534 | 0.61554 | 0.61571 | 0.61585 | 0.61598 | 0.61609 | 0.61619 | 0.61628 | 0.61636 |
| 0.4 | 0.65159 | 0.65191 | 0.65217 | 0.65240 | 0.65260 | 0.65278 | 0.65293 | 0.65307 | 0.65319 | 0.65330 |
| 0.5 | 0.68654 | 0.68694 | 0.68728 | 0.68758 | 0.68783 | 0.68806 | 0.68826 | 0.68843 | 0.68859 | 0.68873 |
| 0.6 | 0.71967 | 0.72017 | 0.72059 | 0.72095 | 0.72127 | 0.72155 | 0.72179 | 0.72201 | 0.72220 | 0.72238 |
| 0.7 | 0.75077 | 0.75136 | 0.75187 | 0.75230 | 0.75268 | 0.75301 | 0.75330 | 0.75356 | 0.75379 | 0.75400 |
| 0.8 | 0.77968 | 0.78037 | 0.78096 | 0.78146 | 0.78190 | 0.78229 | 0.78263 | 0.78293 | 0.78320 | 0.78344 |
| 0.9 | 0.80630 | 0.80709 | 0.80776 | 0.80833 | 0.80883 | 0.80927 | 0.80965 | 0.81000 | 0.81031 | 0.81059 |
| 1.0 | 0.83060 | 0.83148 | 0.83222 | 0.83286 | 0.83341 | 0.83390 | 0.83433 | 0.83472 | 0.83506 | 0.83537 |
| 1.1 | 0.85259 | 0.85355 | 0.85436 | 0.85506 | 0.85566 | 0.85620 | 0.85667 | 0.85709 | 0.85746 | 0.85780 |
| 1.2 | 0.87233 | 0.87335 | 0.87422 | 0.87497 | 0.87563 | 0.87620 | 0.87670 | 0.87715 | 0.87756 | 0.87792 |
| 1.3 | 0.88991 | 0.89099 | 0.89191 | 0.89270 | 0.89339 | 0.89399 | 0.89452 | 0.89500 | 0.89542 | 0.89581 |
| 1.4 | 0.90546 | 0.90658 | 0.90754 | 0.90836 | 0.90907 | 0.90970 | 0.91025 | 0.91074 | 0.91118 | 0.91158 |
| 1.5 | 0.91912 | 0.92027 | 0.92125 | 0.92209 | 0.92282 | 0.92346 | 0.92402 | 0.92452 | 0.92498 | 0.92538 |
| 1.6 | 0.93105 | 0.93221 | 0.93320 | 0.93404 | 0.93478 | 0.93542 | 0.93599 | 0.93650 | 0.93695 | 0.93736 |
| 1.7 | 0.94140 | 0.94256 | 0.94354 | 0.94439 | 0.94512 | 0.94576 | 0.94632 | 0.94683 | 0.94728 | 0.94768 |
| 1.8 | 0.95034 | 0.95148 | 0.95245 | 0.95328 | 0.95400 | 0.95463 | 0.95518 | 0.95568 | 0.95612 | 0.95652 |
| 1.9 | 0.95802 | 0.95914 | 0.96008 | 0.96089 | 0.96158 | 0.96220 | 0.96273 | 0.96321 | 0.96364 | 0.96403 |
| 2.0 | 0.96460 | 0.96567 | 0.96658 | 0.96736 | 0.96803 | 0.96861 | 0.96913 | 0.96959 | 0.97000 | 0.97037 |
| 2.1 | 0.97020 | 0.97123 | 0.97209 | 0.97283 | 0.97347 | 0.97403 | 0.97452 | 0.97495 | 0.97534 | 0.97569 |
| 2.2 | 0.97496 | 0.97593 | 0.97675 | 0.97745 | 0.97805 | 0.97858 | 0.97904 | 0.97945 | 0.97981 | 0.98014 |
| 2.3 | 0.97898 | 0.97990 | 0.98067 | 0.98132 | 0.98189 | 0.98238 | 0.98281 | 0.98319 | 0.98352 | 0.98383 |
| 2.4 | 0.98238 | 0.98324 | 0.98396 | 0.98457 | 0.98509 | 0.98554 | 0.98594 | 0.98629 | 0.98660 | 0.98688 |
| 2.5 | 0.98525 | 0.98604 | 0.98671 | 0.98727 | 0.98775 | 0.98816 | 0.98853 | 0.98885 | 0.98913 | 0.98938 |
| 2.6 | 0.98765 | 0.98839 | 0.98900 | 0.98951 | 0.98995 | 0.99033 | 0.99066 | 0.99095 | 0.99121 | 0.99144 |
| 2.7 | 0.98967 | 0.99035 | 0.99090 | 0.99137 | 0.99177 | 0.99211 | 0.99241 | 0.99267 | 0.99291 | 0.99311 |
| 2.8 | 0.99136 | 0.99198 | 0.99249 | 0.99291 | 0.99327 | 0.99358 | 0.99385 | 0.99408 | 0.99429 | 0.99447 |
| 2.9 | 0.99278 | 0.99334 | 0.99380 | 0.99418 | 0.99450 | 0.99478 | 0.99502 | 0.99523 | 0.99541 | 0.99557 |
| 3.0 | 0.99396 | 0.99447 | 0.99488 | 0.99522 | 0.99551 | 0.99576 | 0.99597 | 0.99616 | 0.99632 | 0.99646 |
| 3.1 | 0.99495 | 0.99541 | 0.99578 | 0.99608 | 0.99634 | 0.99656 | 0.99675 | 0.99691 | 0.99705 | 0.99718 |
| 3.2 | 0.99577 | 0.99618 | 0.99652 | 0.99679 | 0.99702 | 0.99721 | 0.99738 | 0.99752 | 0.99764 | 0.99775 |
| 3.3 | 0.99646 | 0.99683 | 0.99713 | 0.99737 | 0.99757 | 0.99774 | 0.99788 | 0.99801 | 0.99812 | 0.99821 |
| 3.4 | 0.99704 | 0.99737 | 0.99763 | 0.99784 | 0.99802 | 0.99817 | 0.99830 | 0.99840 | 0.99850 | 0.99858 |
| 3.5 | 0.99751 | 0.99781 | 0.99804 | 0.99823 | 0.99839 | 0.99852 | 0.99863 | 0.99872 | 0.99880 | 0.99887 |
| 3.6 | 0.99792 | 0.99818 | 0.99838 | 0.99855 | 0.99869 | 0.99880 | 0.99890 | 0.99898 | 0.99905 | 0.99911 |
| 3.7 | 0.99825 | 0.99848 | 0.99866 | 0.99881 | 0.99893 | 0.99903 | 0.99911 | 0.99918 | 0.99924 | 0.99929 |
| 3.8 | 0.99853 | 0.99874 | 0.99890 | 0.99902 | 0.99913 | 0.99921 | 0.99928 | 0.99934 | 0.99940 | 0.99944 |
| 3.9 | 0.99876 | 0.99894 | 0.99909 | 0.99920 | 0.99929 | 0.99936 | 0.99942 | 0.99948 | 0.99952 | 0.99956 |
| 4.0 | 0.99896 | 0.99912 | 0.99924 | 0.99934 | 0.99942 | 0.99948 | 0.99954 | 0.99958 | 0.99962 | 0.99965 |
| 4.2 | 0.99926 | 0.99938 | 0.99948 | 0.99955 | 0.99961 | 0.99966 | 0.99970 | 0.99973 | 0.99976 | 0.99978 |
| 4.4 | 0.99947 | 0.99957 | 0.99964 | 0.99970 | 0.99974 | 0.99978 | 0.99980 | 0.99983 | 0.99985 | 0.99986 |
| 4.6 | 0.99962 | 0.99969 | 0.99975 | 0.99979 | 0.99983 | 0.99985 | 0.99987 | 0.99989 | 0.99990 | 0.99991 |
| 4.8 | 0.99972 | 0.99978 | 0.99983 | 0.99986 | 0.99988 | 0.99990 | 0.99992 | 0.99993 | 0.99994 | 0.99995 |
| 5.0 | 0.99980 | 0.99985 | 0.99988 | 0.99990 | 0.99992 | 0.99993 | 0.99995 | 0.99995 | 0.99996 | 0.99997 |
| 5.2 | 0.99985 | 0.99989 | 0.99991 | 0.99993 | 0.99995 | 0.99996 | 0.99996 | 0.99997 | 0.99997 | 0.99998 |
| 5.4 | 0.99989 | 0.99992 | 0.99994 | 0.99995 | 0.99996 | 0.99997 | 0.99998 | 0.99998 | 0.99998 | 0.99999 |
| 5.6 | 0.99992 | 0.99994 | 0.99996 | 0.99997 | 0.99997 | 0.99998 | 0.99998 | 0.99999 | 0.99999 | 0.99999 |
| 5.8 | 0.99994 | 0.99996 | 0.99997 | 0.99998 | 0.99998 | 0.99999 | 0.99999 | 0.99999 | 0.99999 | 0.99999 |
| 6.0 | 0.99996 | 0.99997 | 0.99998 | 0.99998 | 0.99999 | 0.99999 | 0.99999 | 0.99999 | ||
| 6.2 | 0.99997 | 0.99998 | 0.99998 | 0.99999 | 0.99999 | 0.99999 |
|
| ||
| 6.4 | 0.99997 | 0.99998 | 0.99999 | 0.99999 | 0.99999 |
|
| |||
| 6.6 | 0.99998 | 0.99999 | 0.99999 | 0.99999 |
|
| ||||
| 6.8 | 0.99999 | 0.99999 | 0.99999 |
|
| |||||
| 7.0 | 0.99999 | 0.99999 |
|
|
Дата: 2018-12-21, просмотров: 378.