тригонометрической и показательной формах
Пусть даны комплексныt числа 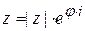 ,
, 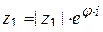 ,
, 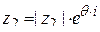 .
.
В показательной и тригонометрической формах записи их можно сравнивать, умножать на число, сопрягать, перемножать, делить, возводить в степень и извлекать из них корни. Рассмотрим эти действия подробнее.
11.3.1 Два комплексных числа равны, когда их модули равны и аргументы
отличаются на число, кратное 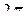 .
.
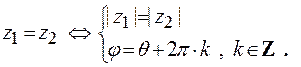
В противном случае комплексные числа различные;
11.3.2 При умножении комплексного числа на действительное число 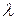 получается число, модуль которого равен |
получается число, модуль которого равен | 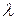 |×|z| и аргумент при
|×|z| и аргумент при 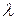 >0 не изменяется либо при
>0 не изменяется либо при 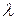 <0 увеличивается на
<0 увеличивается на 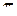 ,
,
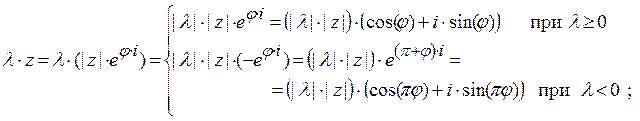
11.3.3 При сопряжении комплексного числа получится число с тем же модулем , но с аргументом противоположного знака,
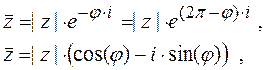
т.е его модуль не меняется, а аргумент изменит знак
(либо вычитается из 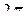 );
);
11.3.4 При умножении числа комплексного числа 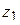 на число
на число 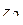 получается число, модуль которого получается умножением модуля числа
получается число, модуль которого получается умножением модуля числа 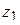 на модуль числа
на модуль числа 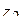 , аргумент получается сложением аргумента числа
, аргумент получается сложением аргумента числа 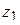 с аргументом числа
с аргументом числа 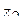 ,
,
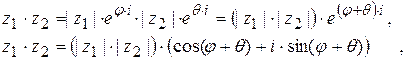
т.е. при умножении двух комплексных чисел их модули перемножаются
а аргументы складываются;
11.3.5 При делении числа 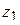 на ненулевое число
на ненулевое число 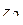 получается число, модуль которого получается делением модуля числа
получается число, модуль которого получается делением модуля числа 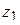 на модуль числа
на модуль числа 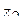 , аргумент получается вычитанием из аргумента числа
, аргумент получается вычитанием из аргумента числа 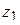 аргумента числа
аргумента числа 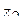 ,
,
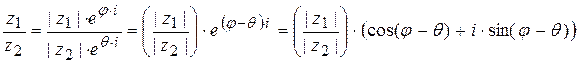 ,
,
т.е. при делении двух комплексных чисел их модули делятся а аргументы вычитаются;
11.3.6 При возведении в натуральную степень n комплексного числа
получается комплексное число, модуль которого является n –й степенью
модуля числа z и аргумент получается умножением аргумента числа z
на натуральное число n ,
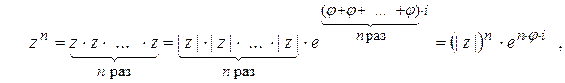
(23) 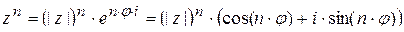 - Формула Муавра ;
- Формула Муавра ;
11.3.7 При извлечении корня степени 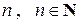 , из комплексного числа
, из комплексного числа
получается множество комплексных чисел, модули которых являются
корнем степени n из модуля числа z, аргумент каждого получается
подстановкой целого числа k в выражение 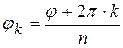 ,
,
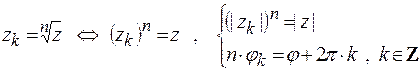 ,
,
(24) 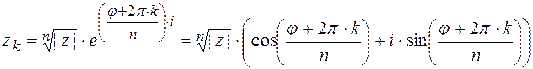
– Формула Муавра – Лапласа.
Среди корней степени 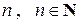 , из комплексного числа z, различных чисел ровно n штук. Они получаются подстановкой последовательно n целых чисел (например к =0, 1, 2, … , n-1 ) в формулу (24). Такие комплексные числа лежат на одной окружности радиуса
, из комплексного числа z, различных чисел ровно n штук. Они получаются подстановкой последовательно n целых чисел (например к =0, 1, 2, … , n-1 ) в формулу (24). Такие комплексные числа лежат на одной окружности радиуса 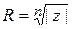 с центром в начале координат и являются вершинами вписанного в такую окружность правильного n- угольника с поворотом начальной вершины на угол
с центром в начале координат и являются вершинами вписанного в такую окружность правильного n- угольника с поворотом начальной вершины на угол 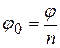 (при к=0), остальные получаются каждый раз поворотом на угол
(при к=0), остальные получаются каждый раз поворотом на угол 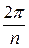 .
.
Пример 15
Даны комплексные числа 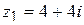 ,
, 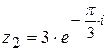 и
и 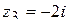 .
.
Найти модули и аргументы чисел 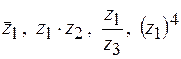 .
.
Найти и изобразить на комплексной плоскости все корни уравнения 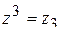 .
.
Решение:
1) Для числа 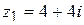 найдём его модуль и аргумент:
найдём его модуль и аргумент:
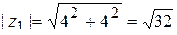 ,
, 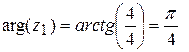 ,
, 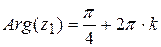 .
.
Тогда  ,
,
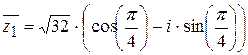 ;
;
2) 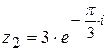 , при этом
, при этом 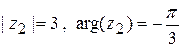 .
.
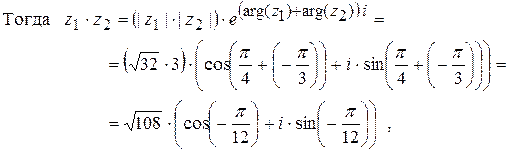
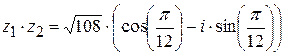 ;
;
3) 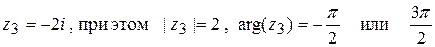 .
.
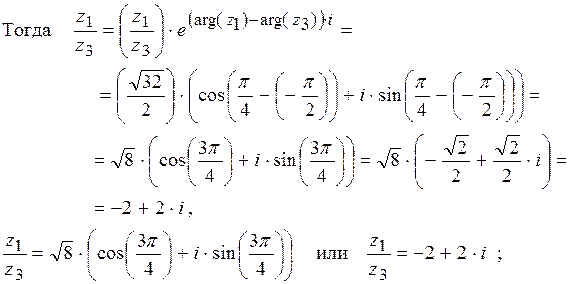
4) 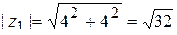 ,
, 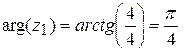 ,
, 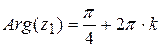 ,
,
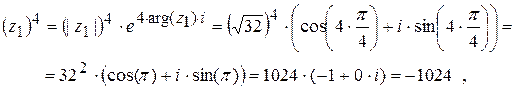
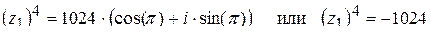 ;
;
5) 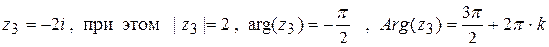 .
.
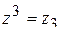
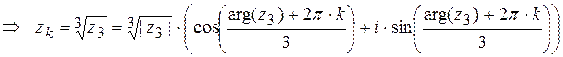 .
.
Подставим последовательно к=0, к=1, к=2:
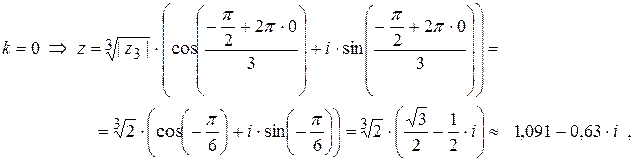
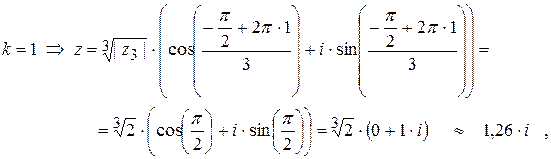
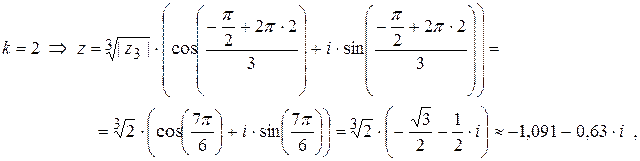
Изобразим найденные решения уравнения 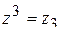 на комплексной плоскости:
на комплексной плоскости:
все три найденных решения лежат на окружности с центром в начале координат и радиусом 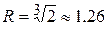 . Три соответствующих точки комплексной плоскости являются вершинами правильного треугольника с поворотом начальной вершины на угол
. Три соответствующих точки комплексной плоскости являются вершинами правильного треугольника с поворотом начальной вершины на угол 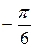 , угол между ними
, угол между ними 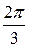 или 1200 .
или 1200 .
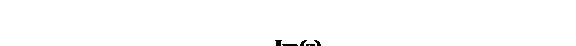
Упражнения
12.1 В треугольнике АВС проведена медиана AD, D – середина стороны ВС.
Доказать, что  .
.
12.2 Дан параллелепипед ABCDA1B1C1D1 , найти суммы векторов:
1) 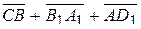 ; 2)
; 2) 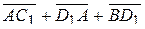 ;
;
3) 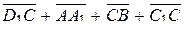 ; 4)
; 4) 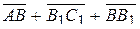 .
.
Ответ:1) 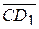 ; 2)
; 2) 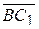 ; 3)
; 3) 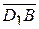 ; 4)
; 4) 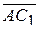 .
.
12.3 Дан тетраэдр ABCD. Найти суммы векторов:
1) 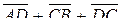 ; 2)
; 2) 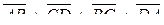 .
.
Ответ:1) 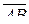 ; 2)
; 2) 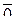 .
.
12.4 Даны три компланарных единичных вектора вектора 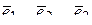 ,
,
причем 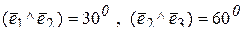 .
.
Построить вектор 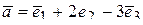 и вычислить его модуль.
и вычислить его модуль.
Ответ: 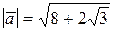 .
.
12.5 Составляющие для скорости направлены под углом 600 друг к другу
и равны соответственно 6 и 4 м/с. Найти скорость результирующего
движения.
Ответ: 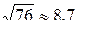 м/с.
м/с.
12.6 В параллелограмме ABCD  , О – точка пересечения
, О – точка пересечения
диагоналей. Выразить векторы 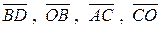 через векторы
через векторы 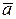 и
и 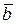 .
.
Ответ:  .
.
12.7 Найти скалярное произведение векторов, модули которых 5 и 6 и угол
между ними равен
1) 450 ; 2) 600 ; 3) 900 ; 4) 1200 ; 5) 1800.
Ответ: 1) 15 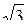 ; 2) 15; 3) 0; 4) -15; 5) -30.
; 2) 15; 3) 0; 4) -15; 5) -30.
12.8 Дано 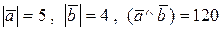 0.
0.
1) 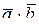 ; 2)
; 2) 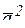 ;
;
3) 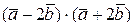 ; 4)
; 4) 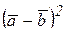 ;
;
5) 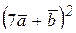 .
.
Ответ: 1)-10; 2) 25; 3) -39; 4) 61; 5) 1101.
12.9 Дано 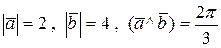 . Найти модуль вектора
. Найти модуль вектора 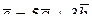 .
.
Ответ: 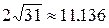 .
.
12.10 Даны три некомпланарных вектора 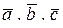 , причем известно, что
, причем известно, что
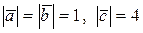 ,
, 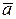 ^
^ 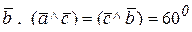 .
.
Найти 1) 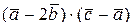 ; 2)
; 2) 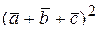 .
.
Ответ: 1) -3; 2) 26.
12.11 Определить длины диагоналей параллелограмма, построенного на
векторах 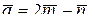 и
и 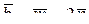 , где
, где  и
и 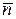 – единичные векторы,
– единичные векторы,
угол между которыми равен 600.
Ответ: 3 и 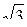 .
.
12.12 Найти скалярное произведение векторов
1) 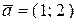 и
и 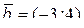 ;
;
2) 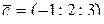 и
и 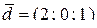 ;
;
3) 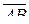 и
и 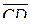 , если А(1; 2; 0), В(0; -1; 3), С(4; -1; 3) и D(2; 0; -2).
, если А(1; 2; 0), В(0; -1; 3), С(4; -1; 3) и D(2; 0; -2).
Ответ: 1) 5; 2) -3; 3) -16.
12.13 При каком значении m векторы 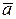 =(4; m; -6) и
=(4; m; -6) и 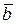 =(m; 2; -7) взаимно
=(m; 2; -7) взаимно
перпендикулярны?
Ответ: -7.
12.14 Найти площадь треугольника АВС, если А(1; 2: 3), В(-1; 3; 1) и С(0; -1; 4).
Ответ: 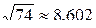 .
.
12.14 Найти объем тетраэдра АBCD, если его вершины A(1; 2; 1), B(3; -1; 2),
C(0; 5; -4) и D(5; 1; 1).
Ответ: 13,5 .
12.15 Записать полярные координаты точек А(0; 3), В(-5; 0), С(2; -4).
Ответ: А(3; 0) , В(5;  ) , С(
) , С( 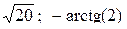 ).
).
12.16 Найти решения уравнения 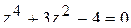 .
.
Ответ: z1=-1, z2=1, z3= – 2i, z4=2i.
12.17 Изобразить на комплексной плоскости решения уравнения
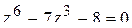 .
.
Ответ: 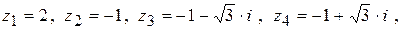

13 Вопросы для самоконтроля
13.1 В чём разница между скалярными и векторными величины? Привести насколько примеров величин обоих видов.
13.2 Перечислите способы построения суммы векторов, чем они отличаются и могут ли получиться разные результаты для одинаковых слагаемых.
13.3 Как построить разность двух векторов, как связана разность векторов с суммой таких векторов?
13.4 Перечислить свойства линейных операций над векторами (сложения, вычитания, умножения на число).
13.5 Будут ли линейно зависимыми противоположные векторы?
13.6 Можно ли взять базисом два ненулевых вектора с углом между ними 600?
13.7 Какие векторы задают аффинные координаты (-1; 0) , (0; 1) , (0; -1) ?
13.8 Что можно сказать о взаимном расположении двух векторов, скалярное произведение которых нулевое, отрицательное, положительное?
13.9 Как найти модуль вектора, заданного своим разложением по аффинному базису с известными модулями базисных векторов и углами между ними?
13.10 Как графически найти координаты точки пространства после введения декартовой системы координат этого пространства?
13.11 Как сложить, вычесть два вектора декартовых координатах и умножить их на число? Перечислить свойства этих операций.
13.12 Перечислить способы нахождения результатов скалярного и векторного произведений двух векторов, заданных координатами. Чем существенно отличаются такие результаты?
13.13 Как разделить отрезок, заданный координатами начала и конца в отношении 3:2 ?
13.14 Перечислить последовательность действий для нахождения площади треугольника, заданного координатами вершин в пространстве.
13.15 Перечислить способ вычисления смешанного произведения трёх векторов и его основные свойства с геометрическим смыслом.
13.16 Как проверить некомпланарность трёх векторов с известными координатами?
13.17 Как найти координаты вектора в аффинном базисе, заданном своими координатами в декартовом базисе?
13.18 Что необходимо задать, чтобы получить полярную систему координат на фиксированной плоскости? Что и как нужно будет измерять, чтобы получать полярные координаты точек плоскости?
13.19 Указать связь между декартовыми и полярными координатами точек плоскости. Каково должно быть взаимное расположение декартовой и полярной систем координат при этом?
14.20 Как перевести комплексное число из алгебраической формы записи в тригонометрическую и показательную. Как выполнить обратное преобразование?
14.21 Записать формулы возведения в степень и извлечения корня из комплексного числа.
14 Контрольное задание
14.1 В базисе 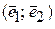 с модулями
с модулями 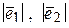 и углом между ними
и углом между ними 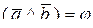
заданы векторы 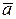 и
и 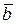 (см. таблицу).
(см. таблицу).
Найти  .
.
|
Вариант | Условия | ||||
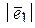
| 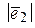
| 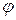
| 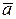
| 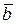
| |
| 1 |  4 4
|  7 7
| j=30о |  =2 =2  -3 -3 
|  =5 =5  + + 
|
| 2 |  4 4
|  5 5
| j=60о |  =2 =2  + + 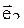
|  =3 =3  + + 
|
| 3 |  5 5
|  3 3
| j=30о |  =2 =2  +3 +3 
|  =4 =4  +6 +6 
|
| 4 |  1 1
| 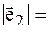 5 5
| j=90о |  =2 =2  - - 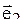
|  =4 =4  + + 
|
| 5 |  3 3
|  5 5
| j=150о |  =3 =3  - - 
|  = =  +2 +2 
|
| 6 |  2 2
|  5 5
| j=45о |  =5 =5  - - 
|  = =  +3 +3 
|
| 7 | 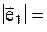 2 2
|  3 3
| j=90о |  =2 =2  - - 
|  =5 =5  +2 +2 
|
| 8 |  4 4
|  3 3
| j=30о |  =2 =2  -3 -3 
|  = =  +3 +3 
|
| 9 |  4 4
|  7 7
| j=135о |  = =  -3 -3 
|  =2 =2  + + 
|
| 10 |  4 4
|  1 1
| j=120о |  =2 =2  - - 
|  =3 =3  -2 -2 
|
| 11 |  5 5
|  2 2
| j=30о |  =2 =2 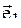 -3 -3 
|  =2 =2  + + 
|
| 12 |  4 4
|  7 7
| j=30о |  =2 =2  -3 -3 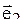
|  =5 =5  + + 
|
| 13 |  4 4
|  2 2
| j=30о |  =2 =2  - - 
|  =3 =3  + + 
|
| 14 |  3 3
|  5 5
| j=150о |  =3 =3  - - 
|  =3 =3  +2 +2 
|
| 15 |  6 6
|  7 7
| j=30о |  =2 =2  - - 
|  = =  +3 +3 
|
| 16 |  4 4
|  3 3
| j=30о |  =3 =3  -2 -2 
|  =3 =3  + + 
|
| 17 |  2 2
|  5 5
| j=90о |  =2 =2  -3 -3 
|  = =  + + 
|
| 18 |  3 3
|  4 4
| j=150о |  =2 =2  -3 -3 
|  = =  +3 +3 
|
| 19 |  2 2
|  3 3
| j=60о |  =2 =2  - - 
|  =5 =5  +2 +2 
|
| 20 |  3 3
|  4 4
| j=150о |  = =  +3 +3 
|  =2 =2  + + 
|
| 21 |  1 1
|  5 5
| j=120о |  =4 =4  -3 -3 
|  = =  + + 
|
| 22 |  3 3
|  4 4
| j=30о |  =2 =2  +4 +4 
|  = =  + + 
|
| Вариант | 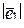
| 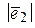
| 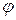
| 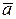
| 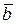
|
| 23 |  4 4
|  2 2
| j=60о |  =2 =2  - - 
|  =2 =2 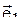 
|
| 24 |  5 5
|  3 3
| j=30о |  =2 =2  - - 
|  = = 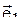 +3 +3 
|
| 25 |  4 4
|  3 3
| j=90о |  =4 =4  -2 -2 
|  = = 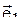 +2 +2 
|
| 26 |  4 4
|  5 5
| j=30о | 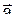 =2 =2 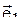 -3 -3 
|  =5 =5 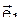 + + 
|
| 27 |  3 3
|  2 2
| j=60о |  = = 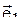 -2 -2 
|  =4 =4 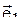 +5 +5 
|
| 28 |  4 4
|  1 1
| j=30о |  =3 =3 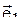 - - 
|  =4 =4 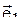 +3 +3 
|
| 29 |  4 4
|  2 2
| j=45о |  = = 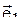 -5 -5 
|  = = 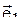 +2 +2 
|
| 30 |  4 4
|  5 5
| j=60о |  =6 =6 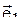 +2 +2 
|  =4 =4 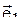 -3 -3 
|
| 31 |  4 4
|  7 7
| j=150о |  = = 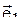 -2 -2 
|  =2 =2 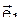 + + 
|
| 32 |  3 3
|  4 4
| j=60о |  =3 =3 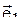 -2 -2 
|  =4 =4 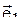 +5 +5 
|
| 33 |  4 4
|  5 5
| j=120о |  =4 =4 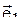 -2 -2 
|  =3 =3 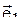 +3 +3 
|
| 34 |  4 4
|  2 2
| j=30о |  =3 =3 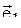 -5 -5 
|  =4 =4 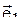 + + 
|
14.2 Даны векторы  ,
,  ,
,  ,
,  (см. таблицу).
(см. таблицу).
Найти для них
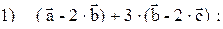
2) 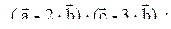
3) Косинусы углов и углы между
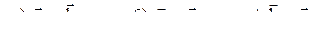
4) 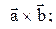
5) Площадь треугольника построенного на векторах 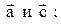
6) Смешанное произведение 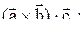
7) Объём пирамиды построенной на 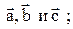
8) Разложение вектора 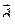 по векторам
по векторам 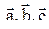 , если они образуют базис.
, если они образуют базис.
| Вариант | 
| 
| 
| 
|
| 1 |  =(1;-5;-1) =(1;-5;-1)
|  =(5;-4;2) =(5;-4;2)
|  =(2;3;4) =(2;3;4)
|  =(3;18;23) =(3;18;23)
|
| 2 |  =(1;-1;1) =(1;-1;1)
|  =(1;2;2) =(1;2;2)
|  =(2;3;-2) =(2;3;-2)
|  =(1;0;5) =(1;0;5)
|
| 3 |  =(1;-2;-1) =(1;-2;-1)
|  =(2;1;2) =(2;1;2)
|  =(2;3;-1) =(2;3;-1)
|  =(6;0;-1) =(6;0;-1)
|
| 4 |  =(1;1;-1) =(1;1;-1)
|  =(-1;3;2) =(-1;3;2)
|  =(2;3;-3) =(2;3;-3)
|  =(-12;-4;19) =(-12;-4;19)
|
| 5 |  =(1;-3;-1) =(1;-3;-1)
|  =(3;2;2) =(3;2;2)
|  =(2;3;-2) =(2;3;-2)
|  =(11;-2;-1) =(11;-2;-1)
|
| 6 |  =(1;-2;-1) =(1;-2;-1)
|  =(2;-2;2) =(2;-2;2)
|  =(2;3;2) =(2;3;2)
|  =(6;12;2) =(6;12;2)
|
| 7 |  =(1;1;-1) =(1;1;-1)
|  =(-1;-1;2) =(-1;-1;2)
|  =(2;3;1) =(2;3;1)
|  =(0;0;-1) =(0;0;-1)
|
| 8 |  =(1;-2;-1) =(1;-2;-1)
|  =(2;5;2) =(2;5;2)
|  =(2;3;-5) =(2;3;-5)
|  =(6;12;23) =(6;12;23)
|
| 9 |  =(1;3;-1) =(1;3;-1)
|  =(-3;-2;2) =(-3;-2;2)
|  =(2;3;2) =(2;3;2)
|  =(1;-8;-3) =(1;-8;-3)
|
| 10 |  =(1;-4;-1) =(1;-4;-1)
|  =(4;3;2) =(4;3;2)
|  =(2;3;-3) =(2;3;-3)
|  =(18;-4;-1) =(18;-4;-1)
|
| 11 |  =(1;3;-1) =(1;3;-1)
|  =(-3;3;2) =(-3;3;2)
|  =(2;3;-3) =(2;3;-3)
|  =(-24;-18;27) =(-24;-18;27)
|
| 12 |  =(1;1;-1) =(1;1;-1)
|  =(-1;4;2) =(-1;4;2)
|  =(2;3;-4) =(2;3;-4)
|  =(15;0;29) =(15;0;29)
|
| 13 |  =(1;-2;-1) =(1;-2;-1)
|  =(2;-3;2) =(2;-3;2)
|  =(2;3;3) =(2;3;3)
|  =(6;20;7) =(6;20;7)
|
| 14 |  =(5;-2;-1) =(5;-2;-1)
|  =(2;-3;0) =(2;-3;0)
|  =(1;3;3) =(1;3;3)
|  =(2;-4;4) =(2;-4;4)
|
| 15 |  =(1;0;-1) =(1;0;-1)
|  =(0;-2;2) =(0;-2;2)
|  =(2;3;2) =(2;3;2)
|  =(4;10;0) =(4;10;0)
|
| 16 |  =(1;-1;-1) =(1;-1;-1)
|  =(1;2;2) =(1;2;2)
|  =(2;3;-2) =(2;3;-2)
|  =(1;0;5) =(1;0;5)
|
| 17 | 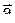 =(1;3;-1) =(1;3;-1)
|  =(-3;0;2) =(-3;0;2)
|  =(2;3;0) =(2;3;0)
|  =(-9;-18;3) =(-9;-18;3)
|
| 18 |  =(1;-2;-1) =(1;-2;-1)
|  =(2;0;2) =(2;0;2)
|  =(2;3;0) =(2;3;0)
|  =(6;2;-2) =(6;2;-2)
|
| 19 |  =(1;0;-1) =(1;0;-1)
|  =(0;3;2) =(0;3;2)
|  =(2;3;-3) =(2;3;-3)
|  =(-6;0;15) =(-6;0;15)
|
| 20 |  =(1;-1;-1) =(1;-1;-1)
|  =(1;-3;2) =(1;-3;2)
|  =(2;3;3) =(2;3;3)
|  =(6;20;5) =(6;20;5)
|
| 21 |  =(1;-2;-1) =(1;-2;-1)
|  =(2;0;2) =(2;0;2)
|  =(2;3;0) =(2;3;0)
|  =(6;2;-2) =(6;2;-2)
|
| Вариант | 
| 
| 
| 
|
| 22 |  =(1;3;-1) =(1;3;-1)
|  =(-3;2;2) =(-3;2;2)
|  =(2;3;-2) =(2;3;-2)
|  =(-19;-20; 17) =(-19;-20; 17)
|
| 23 |  =(1;2;-1) =(1;2;-1)
|  =(-2;4;2) =(-2;4;2)
|  =(2;3;-4) =(2;3;-4)
|  =(-22;-6; 34) =(-22;-6; 34)
|
| 24 |  =(1;3;-1) =(1;3;-1)
|  =(-3;-3;2) =(-3;-3;2)
|  =(2;3;3) =(2;3;3)
|  =(6;0;-3) =(6;0;-3)
|
| 25 |  =(1;-2;-1) =(1;-2;-1)
|  =(2;-4;2) =(2;-4;2)
|  =(2;3;4) =(2;3;4)
|  =(6;30;14) =(6;30;14)
|
| 26 |  =(1;-2;-1) =(1;-2;-1)
|  =(2;-4;2) =(2;-4;2)
| 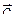 =(2;3;4) =(2;3;4)
|  =(6;30;14) =(6;30;14)
|
| 27 |  =(1;-2;-1) =(1;-2;-1)
|  =(2;2;2) =(2;2;2)
|  =(2;3;-2) =(2;3;-2)
|  =(6;0;2) =(6;0;2)
|
| 28 | 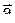 =(1;3;-1) =(1;3;-1)
|  =(-3;-3;2) =(-3;-3;2)
|  =(2;3;3) =(2;3;3)
|  =(6;0;-3) =(6;0;-3)
|
| 29 |  =(1;0;-1) =(1;0;-1)
|  =(0;-5;2) =(0;-5;2)
|  =(2;3;5) =(2;3;5)
|  =(10;40;15) =(10;40;15)
|
| 30 |  =(1;-5;-1) =(1;-5;-1)
|  =(5;-5;2) =(5;-5;2)
|  =(2;3;5) =(2;3;5)
|  =(0;30;25) =(0;30;25)
|
| 31 | 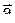 =(1;-5;-1) =(1;-5;-1)
|  =(5;-4;2) =(5;-4;2)
|  =(2;3;4) =(2;3;4)
|  =(3;18;23) =(3;18;23)
|
| 32 |  =(1;-1;1) =(1;-1;1)
|  =(1;2;2) =(1;2;2)
|  =(2;3;-2) =(2;3;-2)
|  =(1;0;5) =(1;0;5)
|
| 33 |  =(1;-2;-1) =(1;-2;-1)
|  =(2;-1;2) =(2;-1;2)
|  =(2;3;1) =(2;3;1)
|  =(6;6;-1) =(6;6;-1)
|
| 34 |  =(1;1;-1) =(1;1;-1)
|  =(-1;3;2) =(-1;3;2)
|  =(2;3;-3) =(2;3;-3)
|  =(-12;-4;19) =(-12;-4;19)
|
14.3 Точка А(х; у ) задана декартовыми координатами найти её полярные
координаты. Точка В( 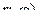 задана полярными координатами найти её
задана полярными координатами найти её
декартовы координаты.
| Вариант | А(х; у ) | В( 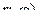
|
| 1 | (-1; 2) | (5; 1) |
| 2 | (-3; -3) | (3; 3) |
| 3 | (4; -2) | (4; 2) |
| 4 | (-4; 0) | (3;-2 ) |
| 5 | (3; -4) | (8; -3) |
| 6 | (-1; -1) | (2; 6) |
| 7 | (-3; -2) | (5; 3) |
| 8 | (3; -3) | (10; 2) |
| 9 | (4; -1) | (3; -1,5) |
| 10 | (5; 2) | (2; 2,5) |
| 11 | (1; 3) | (3; -3) |
| 12 | (2; -4) | (5; 0,5) |
| 13 | (-2; -2) | (4; -5) |
| 14 | (-4; 3) | (3; 2) |
| 15 | (2; -1) | (1; -2) |
| 16 | (0; -6) | (2; 3) |
| 17 | (3; -1) | (2; 3,2) |
| 18 | (-1; 3) | (4; -3) |
| 19 | (-6; 0) | (8; -6) |
| 20 | (3; 1) | (3; 6) |
| 21 | (2; 5) | (2; -4,2) |
| 22 | (-2; 6) | (3; 3,2) |
| 23 | (-5; -5) | (5; 0,4) |
| 24 | (-3; -1) | (4; -3) |
| 25 | (-2; 6) | (10; -1) |
| 26 | (3; -1) | (2; -5,2) |
| 27 | (-4; 0) | (2; 4,1) |
| 28 | (3; 0) | (3,2; -1) |
| 29 | (5; -5) | (5,4; 1) |
| 30 | (4; 6) | (3; -1,8) |
| 31 | (2; -6) | (4,2; -7) |
| 32 | (-4; 4) | (10; 3,1) |
| 33 | (2; 3) | (2,4; -2) |
| 34 | (0; 6) | (5; 0) |
14.4 Даны комплексные числа
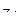 = a1+b1× i ,
= a1+b1× i , 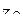 = a2+b2×i ,
= a2+b2×i , 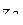 = a3+b3× i ,
= a3+b3× i , 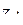 = a4+b4× i (см. таблицу).
= a4+b4× i (см. таблицу).
Для них
1) Найти 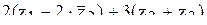 ;
;
2) Найти 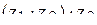 и
и 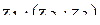 ;
;
3) Найти  ;
;
4) Найти произведение матриц с комплексными элементами
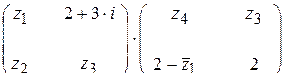 ;
;
5) Изобразить на комплексной плоскости числа 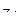 ,
, 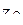 ,
, 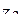 .
.
Найти их модули и аргументы, записать в тригонометрической и
показательной формах;
6) Найти решения уравнений
а) 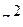 + b×z + c =0 (см. таблицу);
+ b×z + c =0 (см. таблицу);
б) z= 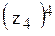 ;
;
в) 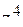 =
= 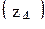 .
.
(Все вычисления производить с округлением до двух знаков после запятой, все углы находить в градусах (либо в радианах)).
| Вар. | Числа |
| |||
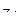
| 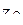
| 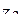
| 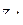
| ||
| 1 | 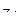 =-1-i =-1-i
| 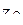 =1-4i =1-4i
| 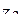 = -2 = -2
| 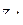 =2-3i =2-3i
|  +4z+13=0 +4z+13=0
|
| 2 | 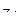 =3+2i =3+2i
| 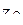 =-1-2i =-1-2i
| 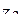 = -1-5i = -1-5i
| 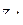 =3-5i =3-5i
|  -10z+29=0 -10z+29=0
|
| 3 | 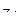 =3-3i =3-3i
| 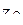 =-1-4i =-1-4i
| 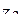 =-1-5i =-1-5i
|  =3-5i =3-5i
|  -6z+25=0 -6z+25=0
|
| 4 | 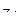 =-3i =-3i
| 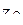 =1-4i =1-4i
| 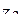 =-2i =-2i
|  =2-2i =2-2i
|  +12z+40=0 +12z+40=0
|
| 5 | 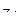 =-1-4i =-1-4i
| 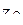 =-3-4i =-3-4i
| 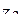 =1+i =1+i
|  =4-4i =4-4i
|  +6z+45=0 +6z+45=0
|
| 6 | 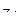 =-4i =-4i
| 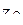 =3-4i =3-4i
|  =3+i =3+i
|  =4-4i =4-4i
|  -8z+41=0 -8z+41=0
|
| 7 | 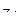 =-3i =-3i
| 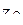 =-1-4i =-1-4i
|  =-2-4i =-2-4i
|  =2-6i =2-6i
|  +8z+41=0 +8z+41=0
|
| 8 | 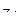 =3-2i =3-2i
| 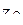 =-3-2i =-3-2i
|  =-2-i =-2-i
|  =3-3i =3-3i
|  +4z+13=0 +4z+13=0
|
| 9 | 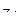 =-1-2i =-1-2i
|  =-3-4i =-3-4i
|  =1-i =1-i
|  =3-3i =3-3i
|  -4z+68=0 -4z+68=0
|
| 10 | 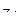 =-3i =-3i
|  =-1-4i =-1-4i
|  =-1-6i =-1-6i
|  =2-5i =2-5i
|  +2z+26=0 +2z+26=0
|
| 11 | 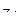 =-4i =-4i
|  =1-4i =1-4i
|  =-3-3i =-3-3i
|  =4-2i =4-2i
|  +2z+17=0 +2z+17=0
|
| 12 | 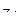 =-4i =-4i
|  =3-4i =3-4i
|  =-1-3i =-1-3i
|  =3-2i =3-2i
|  -16z+65=0 -16z+65=0
|
| Вар. | Числа |
| |||
| 
| 
| 
| ||
| 13 | 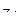 =1-4i =1-4i
|  =-1-4i =-1-4i
|  =i =i
|  =5-4i =5-4i
|  -10z+34=0 -10z+34=0
|
| 14 | 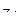 =3-2i =3-2i
|  =-3-2i =-3-2i
|  =2-5i =2-5i
|  =2-6i =2-6i
|  +10z+50=0 +10z+50=0
|
| 15 | 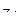 =-2i =-2i
|  =-3-4i =-3-4i
|  =-2-5i =-2-5i
|  =2-6i =2-6i
|  +16z+53=0 +16z+53=0
|
| 16 | 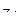 =-3i =-3i
|  =-1-4i =-1-4i
|  =-1-2i =-1-2i
|  =4-3i =4-3i
|  +6z+58=0 +6z+58=0
|
| 17 | 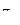 =1-3i =1-3i
|  =-1-4i =-1-4i
|  =-1+i =-1+i
|  =4-5i =4-5i
|  +16z+68=0 +16z+68=0
|
| 18 | 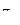 =-4i =-4i
|  =1-4i =1-4i
|  =2+i =2+i
|  =3-5i =3-5i
|  -20z+125=0 -20z+125=0
|
| 19 | 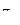 =2-i =2-i
|  =-3-4i =-3-4i
|  =1-4i =1-4i
|  =5-2i =5-2i
|  -6z+18=0 -6z+18=0
|
| 20 | 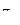 =3-4i =3-4i
|  =3-2i =3-2i
|  =1-i =1-i
|  =2-4i =2-4i
|  -14z+74=0 -14z+74=0
|
| 21 | 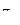 =1-4i =1-4i
|  =4-4i =4-4i
|  =-i =-i
|  =2-4i =2-4i
|  -4z+85=0 -4z+85=0
|
| 22 | 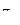 =-3i =-3i
|  =1-4i =1-4i
|  =-1-6i =-1-6i
|  =3-6i =3-6i
|  -18z+85 -18z+85
|
| 23 | 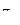 =2-4i =2-4i
|  =-1-4i =-1-4i
|  =-2-3i =-2-3i
|  =3-3i =3-3i
|  +6z+90=0 +6z+90=0
|
| 24 | 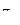 =-i =-i
|  =1-4i =1-4i
|  =-2-3i =-2-3i
|  =2-3i =2-3i
|  -18z+90=0 -18z+90=0
|
| 25 | 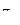 =3-3i =3-3i
|  =-3-4i =-3-4i
|  =-2-3i =-2-3i
|  =4-5i =4-5i
|  -12z+61=0 -12z+61=0
|
| 26 | 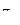 =3-4i =3-4i
|  =3-2i =3-2i
|  =-5i =-5i
|  =4-2i =4-2i
|  -16z+65=0 -16z+65=0
|
| 27 | 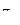 =2-4i =2-4i
|  =-1-4i =-1-4i
|  =2-5i =2-5i
|  =2-2i =2-2i
|  +12z+45=0 +12z+45=0
|
| 28 | 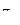 =-3i =-3i
|  =-3-4i =-3-4i
|  =-2-2i =-2-2i
|  =3-4i =3-4i
|  +14z+85=0 +14z+85=0
|
| 29 | 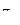 =3-4i =3-4i
|  =-3-4i =-3-4i
|  =2+i =2+i
|  =3-6i =3-6i
|  +18z+117=0 +18z+117=0
|
| 30 | 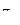 =-3 =-3
|  =-1-4i =-1-4i
|  =1+i =1+i
|  =2-6i =2-6i
|  +18z+106=0 +18z+106=0
|
| 31 | 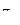 =-1-i =-1-i
|  =1-4i =1-4i
|  =-4i =-4i
|  =4-3i =4-3i
|  +10z+86=0 +10z+86=0
|
| 32 | 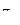 =3-4i =3-4i
|  =3-2i =3-2i
|  =-1-i =-1-i
|  =3-5i =3-5i
|  +20z+136=0 +20z+136=0
|
| 33 | 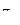 =3-4i =3-4i
|  =-1-4i =-1-4i
|  =-1-i =-1-i
|  =5-5i =5-5i
|  -16z+82=0 -16z+82=0
|
| 34 | 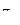 =-4i =-4i
|  =-3-4i =-3-4i
|  =-2-6i =-2-6i
|  =2-2i =2-2i
|  -14z+98=0 -14z+98=0
|
Шпаргалка
· Скалярное произведение  ×
× 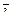 =|
=|  |×|
|×|  |×cos(j);
|×cos(j);
· Проекция вектора на ось прl  =|
=|  |×cos(
|×cos(  ^ l);
^ l);
· Декартов базис если 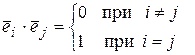 ;
;
· Если даны векторы 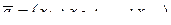 и
и 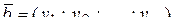 ,
,
то для них:
1) равенство 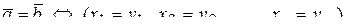 ;
;
2) сумма 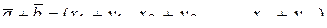 ;
;
3) умножение на число 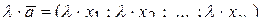 ;
;
4) скалярное произведение 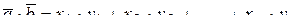 ;
;
5) модули 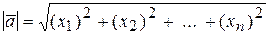
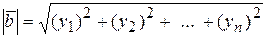 ;
;
6) ортогональность: Если  ¹0
¹0 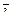 ¹0 и
¹0 и 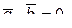 то
то 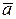 ^
^ 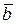 ;
;
7) косинус угла 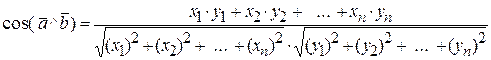 ; 8)
; 8) 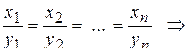 векторы
векторы  и
и 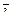 коллинеарны.
коллинеарны.
· Для точек 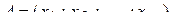 и
и 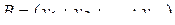
1) вектор 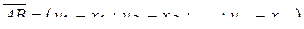
2) расстояние |АB|= 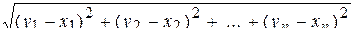
3) середина 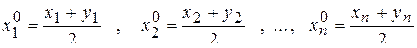 .
.
· Модуль векторного произведения 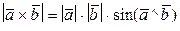 ;
;
· Векторное произведение базисных векторов декартова базиса ( 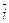 ;
; 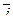 ;
; 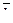 )
)
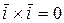
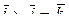
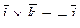
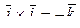
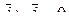
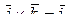
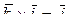
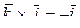
 ;
;
· Площадь треугольника АВС 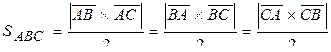 ;
;
· Векторное произведение в координатной форме 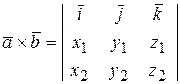 ;
;
· sin (  ^
^ 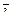 )=
)= 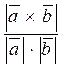 =
= 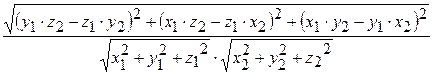 ;
;
· Двойное векторное произведение 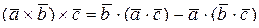 ;
;
· Смешанное произведение 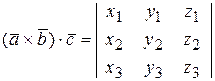 ;
;
· 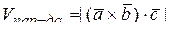
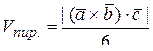 ;
;
· Декартовы координаты по полярным 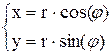 ;
;
· Полярные координаты по декартовым r = 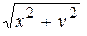 ,
, 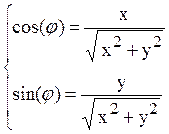 ;
;
· Действия над комплексными числами в алгебраической форме  :
:
1) 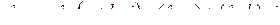 ;
;
2)  ;
;
3) 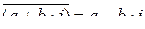 ;
;
4) 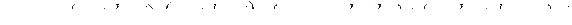 ;
;
5) 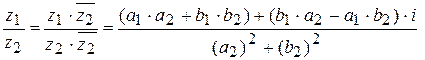 ;
;
· z = |z|× ( cos( 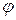 ) + i×sin(
) + i×sin( 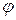 )) – тригонометрическая форма записи
)) – тригонометрическая форма записи
комплексного числа;
· 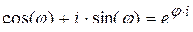 – Формула Эйлера;
– Формула Эйлера;
· 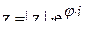 – показательная форма записи комплексного числа,
– показательная форма записи комплексного числа,
где 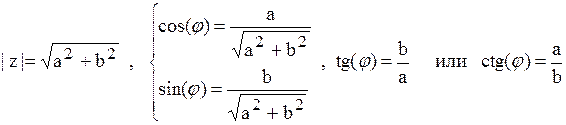 ;
;
· Действия над комплексными числами в тригонометрической (показательной) формах :
1) 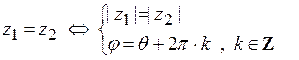 ;
; 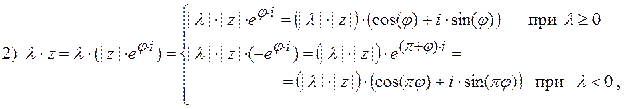
3) 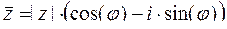 ;
;
4) 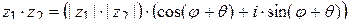 ;
;
5) 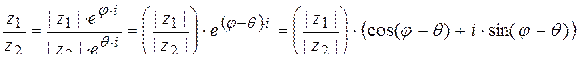 ;
;
6) 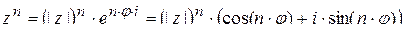 - Формула Муавра ;
- Формула Муавра ;
7) 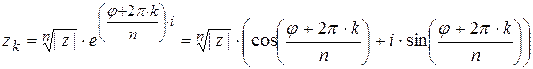
– Формула Муавра – Лапласа.
13 Рекомендуемая литература
13.1 Бугров Я.С., Никольский С.М. Элементы линейной алгебры и
аналитической геометрии. – М.: Наука, 1980 – 176с.
13.2 Фролов С.В., Шостак Р.Я. Курс высшей математики. Т.1
– М.: Высшая школа, 1973 – 480с.
13.3 Шнейдер В.Е., Слуцкий А.И., Шумов А.С. Краткий курс высшей
математики Т.1 – М.: Высшая школа, 1978.
13.4 Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в
примерах и задачах. Ч. 1 – М.: Высшая школа, 1986 – 304, 416 с.
13.5 Шипачев В.С. Высшая математика: Учебное пособие для ВУЗов.
– М.: Высшая школа, 1996 – 479с.
13.6 Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры.
– М.: Наука, 1971 – 320с.
13.7 Власов В.Г. Конспект лекций по высшей математике. –
–М.: Айрис, 1998 – 288с.
13.8 Курош А.Г. Курс высшей алгебры. – М.: 1963 – 431с.
13.9 Орлов Ю.В. Линейная алгебра и аналитическая геометрия
часть 1 «Матричное исчисление. Решение систем линейных уравнений»
Учебно-методическое пособие по курсу «Высшая математика»
для бакалавров направления 080200.62 «Менеджмент».
–Новоуральск, НГТИ 2012 - 72 с.
Орлов Юрий Владимирович
Линейная алгебра и аналитическая геометрия
Часть 2 «Векторное исчисление»
Учебное-методическое пособие по курсу «ВЫСШАЯ МАТЕМАТИКА» для бакалавров направления 210100 «Электроника и наноэлектроника»
Новоуральск изд. НГТИ, 2012. −72 с.
Макет подготовлен на кафедре ВМ НТИ НИЯУ МИФИ
Подписано в печать _______________ Формат А5 Гарнитура
Печать плоская. Усл-печ. л. ________ Тираж _______ экз. Заказ _______
Отпечатано на ризографе НТИ
Издательство Новоуральского технологического института НИЯУ МИФИ,
624130, г.Новоуральск, ул. Ленина 85, НГТИ
Дата: 2018-12-21, просмотров: 439.