В математике выполняются действия с числами, которые берутся из некоторых числовых множеств. Основными числовыми множествами являются множества натуральных, целых, рациональных, иррациональных и действительных чисел:
N – множество натуральных чисел, N={1, 2, 3, … , n , n+1, … };
Z – множество целых чисел, Z={0, 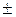 1,
1, 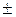 2,
2, 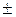 3, … };
3, … };
Q – множество рациональных чисел, Q={ x | 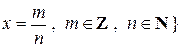 .
.
Всякое рациональное число записывается в виде бесконечной
десятичной периодической дроби,
например 1 = 1,0000(0)… , 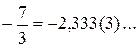 ,
,
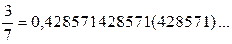 ;
;
I – множество иррациональных чисел,
элементы которого – бесконечные десятичные непериодические
дроби, 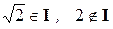 ,
, 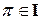 ;
;
R – множество действительных чисел, 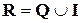
( 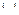 - знак объединения множеств).
- знак объединения множеств).
Все перечисленные числовые множества являются подмножествами множества действительных чисел, N 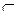 R, Z
R, Z 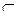 R, Q
R, Q 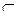 R, I
R, I 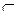 R .
R .
В результате сложения, вычитания, произведения и частного (при ненулевом знаменателе) для действительных чисел результат также принадлежит множеству действительных чисел. Применение же некоторых функций к действительным числам требует сужения множества R :
квадратный корень определён только для неотрицательных чисел, логарифм определён только для положительных чисел и т.д. Не всякий многочлен на множестве действительных чисел имеет действительные корни,
например 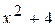 действительных корней не имеет.
действительных корней не имеет.
Всязи с этим потребовалось расширить и множество действительных чисел, как введение нуля и отрицательных чисел исторически расширило множество натуральных чисел до множества целых чисел, которое в свою очередь расширилось до множества рациональных чисел.
Опр.26 Мнимой единицей назовем число, квадрат которого равен – 1 , обозначим такое число буквой i .
На множестве действительных чисел нет чисел, квадрат которых равен отрицательному числу, следовательно 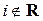 т.е. получили число, не принадлежащее множеству действительных чисел. Мнимую единицу можно записывать
т.е. получили число, не принадлежащее множеству действительных чисел. Мнимую единицу можно записывать 
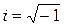 (один из корней, аналог арифметического корня).
(один из корней, аналог арифметического корня).
11.2 Алгебраическая форма комплексного числа
Опр.27 Комплексным числом называется число z вида (20) z = a + b × i ,
где а 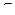 R, а – действительная часть числа z, a=Re (z),
R, а – действительная часть числа z, a=Re (z),
b 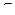 R, b – мнимая часть числа z , b = Im (z),
R, b – мнимая часть числа z , b = Im (z),
i – мнимая единица.
Такая форма записи комплексного числа называется алгебраической.
Комплексные числа можно обозначать и парой действительных чисел, из
которых первое является действительной частью, а второе является
мнимой частью такого числа: z = (a; b).
Множество комплексных чисел будем обозначать С.
Пример 11
Найти решения уравнения 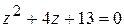 .
.
Решение:
На множестве действительных чисел уравнение 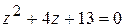 решений не имеет, т.к. его дискриминант
решений не имеет, т.к. его дискриминант 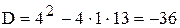 , D < 0.
, D < 0.
На множестве комплексных чисел найдем решение данного уравнения, воспользовавшись формулой нахождения корней квадратного уравнения :
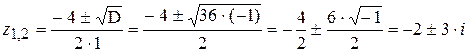 .
.
Ответ: 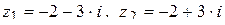 .
.
Замечание: Если мнимая часть комплексного числа равна нулю, то z = a является действительным числом т.е. все действительные числа являются при этом и комплексными (с нулевой мнимой частью). Множество действительных чисел вкладывается в множество комплексных чисел, 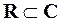 .
.
Если действительная и мнимая части комплексного числа нулевые, то число называется нулём и записывают это z = 0 .
Дата: 2018-12-21, просмотров: 371.