Если 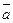 =( x 1 ; y 1 ; z 1 ) и
=( x 1 ; y 1 ; z 1 ) и 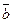 =( x 2 ; y 2 ; z 2 ) , то
=( x 2 ; y 2 ; z 2 ) , то
(11.1) 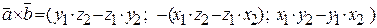 .
.
Выведем эту формулу:
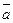
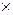
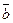 =( x 1 ×
=( x 1 × 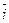 + y 1 ×
+ y 1 × 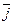 + z ×
+ z × 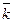 )
) 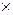 ( x 2 ×
( x 2 × 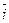 + y 2 ×
+ y 2 × 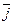 + z ×
+ z × 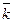 )=
)=
= х 1 x2 × ( 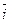
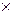
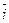 ) + x1y2 × (
) + x1y2 × ( 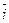
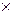
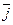 ) + x1z2 × (
) + x1z2 × ( 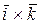 )+
)+
+ y1x2 × ( 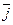
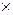
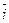 ) + y1y2 × (
) + y1y2 × ( 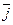
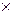
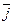 ) + y1z2 × (
) + y1z2 × ( 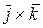 )+
)+
+ z 1 x 2 × ( 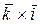 )+ z 1 y 2 × (
)+ z 1 y 2 × ( 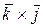 ) + z 1 z 2 × (
) + z 1 z 2 × ( 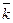
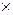
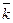 ).
).
Векторы 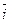 ,
, 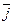 ,
, 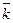 ортонормированны, тройка (
ортонормированны, тройка ( 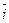 ,
, 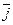 ,
, 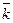 ) – правая,
) – правая,
тогда при учете свойства 8.5 получим
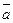
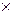
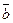 = х1 x 2 × 0 + x 1 y 2 ×
= х1 x 2 × 0 + x 1 y 2 × 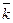 + x 1 z 2 × (-
+ x 1 z 2 × (- 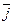 ) +
) +
+ y1x2 × (- 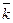 ) + y1y2 × 0 + y1z2 ×
) + y1y2 × 0 + y1z2 × 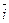 +
+
+ z1x2 × 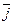 + z1y2 × (-
+ z1y2 × (- 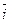 ) + z1z2 × 0 =
) + z1z2 × 0 =
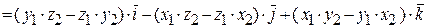 .
.
Если дополнительно заменить каждую скобку соответствующим определителем второго порядка
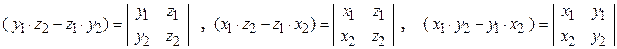 ,
,
то получим правило раскрытия определителя третьего порядка по первой строке (не вдаваясь в смысл 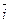 ,
, 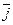 ,
, 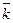 считаем их элементами первой строки).
считаем их элементами первой строки).
Получили правило, по которому легко запомнить правило нахождения векторного произведения векторов в координатной форме:
(11.2) 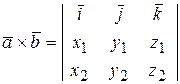 ;
;
Если векторы двумерные, то можно считать их третью координату нулевой,
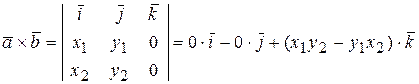 .
.
8.5 Синус угла между векторами, заданными в координатной форме
(12) sin ( 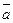 ^
^ 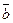 )=
)= 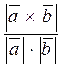 =
= 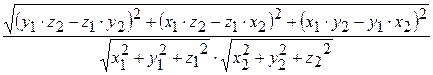 ;
;
8.6 Двойное векторное произведение 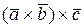 или
или 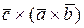 - вектор,
- вектор,
компланарный с 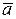 и
и  , он может быть найден по правилу
, он может быть найден по правилу
(13) 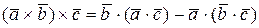 .
.
Двойное векторное произведение не обладает ни коммутативностью, ни
дистрибутивностью.
Пример 6
Базисом являются векторы 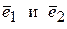 ,
, 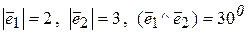 .
.
В этом базисе заданы векторы 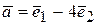 ,
, 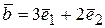 .
.
Найти модуль векторного произведения векторов 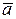 и
и  .
.
Решение:
Составим векторное произведение векторов 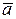 и
и  :
:
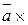
 =(
=( 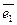 – 4
– 4 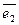 )
) 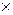 (3
(3 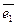 +2
+2 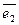 )=
)=
= 
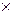 3
3 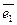 +
+ 
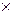 2
2 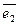 +(-4
+(-4 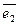 )
) 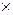 3
3 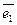 +(-4
+(-4 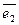 )
) 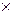 2
2 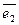 =
=
= 3×( 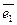
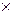
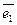 ) + 2×(
) + 2×( 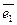
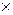
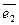 ) – 12×(
) – 12×( 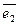
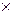
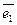 ) – 8×(
) – 8×( 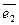
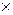
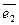 )=
)=
= 3×( 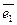
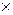
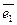 ) + 2×(
) + 2×( 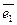
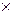
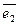 ) + 12×(
) + 12×( 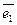
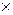
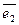 ) – 8×(
) – 8×( 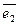
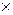
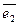 )=
)=
= 3×0 +14( 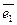
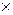
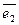 )– 8×0= 14×(
)– 8×0= 14×( 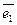
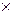
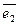 ).
).
Получили 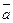
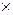
 = 14×(
= 14×( 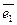
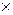
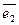 ), |
), | 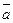
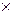
 |= 14×|
|= 14×| 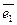
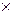
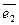 |.
|.
По определению 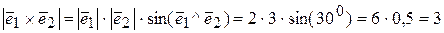 ,
,
| 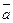
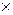
 |= 14×|
|= 14×| 
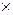
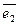 |= 14×3 = 42.
|= 14×3 = 42.
Ответ: | 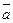
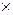
 |= 42.
|= 42.
Пример 7
Найти площадь треугольника АВС с вершинами в точках пространства А(2; 4; -1), В(3; 1; 1), С(0; 4; 2). Найти внутренний угол треугольника при вершине А и синус этого угла.
Решение:
1) Найдем векторы 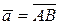 и
и 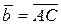 , образующие данный треугольник.
, образующие данный треугольник.
Координаты вектора находятся вычитанием из координат конечной точки соответствующих координат начальной точки:
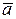 =(3 – 2; 1 – 4; 1 – (-1)) = (1; -3; 2),
=(3 – 2; 1 – 4; 1 – (-1)) = (1; -3; 2),  =(0 – 2; 4 – 4; 2 – (-1))= (-2; 0; 3). Треугольник АВС образован векторами
=(0 – 2; 4 – 4; 2 – (-1))= (-2; 0; 3). Треугольник АВС образован векторами 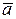 =(1; -3; 2) и
=(1; -3; 2) и  =(-2; 0; 3);
=(-2; 0; 3);
2) Площадь треугольника равна половине модуля векторного произведения
образующих треугольник векторов, т.е. 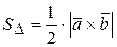 .
.
Векторное произведение векторов 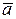 и
и  в координатной форме имеет вид:
в координатной форме имеет вид:
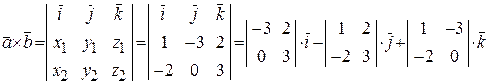 =
=
= 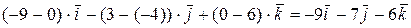 ,
,
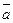
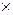
 =(-9; -7; -6).
=(-9; -7; -6).
Модуль векторного произведения 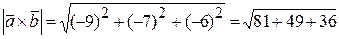 =
= 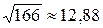 ,
,
следовательно 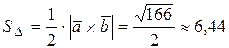 ;
;
3) Угол при вершине А равен углу между отрезками АВ и АС, следовательно и между соответствующими векторами 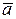 и
и  .
.
Угол между векторами можно найти по его косинусу, используя скалярное произведение векторов:
cos( 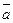 ^
^ 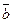 )=
)= 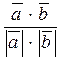 =
= 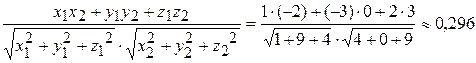 .
.
При этом синус угла можно найти из основного тригонометрического тождества 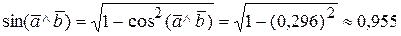 .
.
В данном случае синус угла между векторами вычислим непосредственно, используя модуль векторного произведения (который уже найден):
sin( 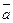 ^
^ 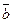 )=
)= 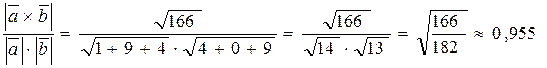 .
.
Найдём угол между векторами : ( 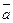 ^
^ 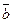 )= arcsin(0,955 )
)= arcsin(0,955 ) 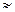 730.
730.
Ответ: S=6,44 , sin(ВАС)=0,883 , (ВА^ВС)  730.
730.
9 Смешанное произведение векторов
Опр.24 Произведение трёх векторов называется смешанным, если результат векторного произведения двух таких векторов скалярно умножается на третий вектор, если оно имеет вид 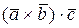 или
или 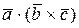 . Результатом смешанного произведения трёх векторов является число.
. Результатом смешанного произведения трёх векторов является число.
9.1 Свойства смешанного произведения
9.1.1 В координатной форме смешанное произведение трёх векторов трёхмерного пространства равно определителю матрицы, для которой векторы являются строками (столбцами),
(14) 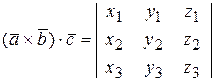 .
.
В самом деле, 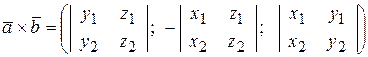 ,
,
тогда 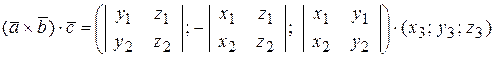 =
=
= 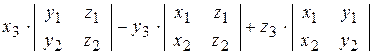 =
= 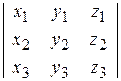
т.к является раскрытием определителя по третьей строке;
9.1.2 Результат смешанного произведения не зависит от последовательности
скалярного и векторного произведений, 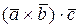 =
= 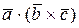 .
.
В 9.1.1 выведено, что 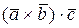 =
= 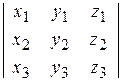 .
.
Выполним аналогичные преобразования для 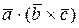 :
:
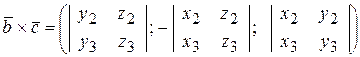 ,
,
тогда 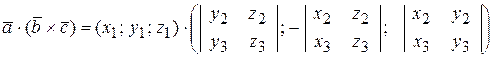 =
=
= 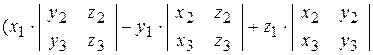 =
= 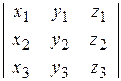 ,
,
т.к. получили раскрытие определителя по первой строке;
Получили, что можно не указывать последовательность действий и смешанное произведение иногда обозначают 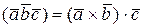 =
= 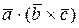 ;
;
9.1.3 При перестановке двух сомножителей в смешанном произведении
результат изменит знак, 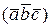 =
= 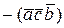 .
.
Все шесть возможных комбинаций смешанных произведений трёх
векторов разбились на две части:
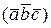 =
= 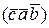 =
= 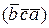 =
= 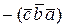 =
= 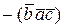 =
= 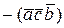 .
.
9.1.4 Постоянную можно выносить из смешанного произведения ,
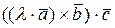 =
= 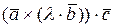 =
= 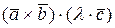 =
= 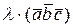 ;
;
9.1.5 Смешанное произведение компланарных векторов равно нулю.
Свойства 9.1.3 , 9.1.4 и 9.1.5 вытекают из того, что смешанное произведение трёх векторов равно определителю, т.е. обладает свойствами определителя: при перестановке двух строк (столбцов) определитель изменяет знак, множитель строки (столбца) выносится за знак определителя, определитель линейно зависимых строк (столбцов) равен нулю. По утв.5 три и более компланарных вектора линейно зависимы.
Справедливо и обратное: равенство нулю смешанного произведения трёх векторов говорит о их компланарности;
Дата: 2018-12-21, просмотров: 445.