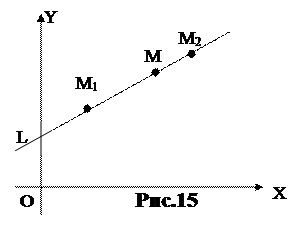
Пусть на плоскости Оxy заданы две различные точки M1(x 1 ; y 1) и М2(x 2 ; y 2).
Проведем через эти точки прямую L, пусть М (х; у) - некоторая точка прямой L, не совпадающая с М2 (рис.15).
Точка М делит отрезок М1М2 в отношении l , если (13) 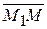 =l×
=l× 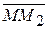 .
.
 |
Очевидно, что:
1) l>0 лишь в случае, когда точка М
лежит между точками М1 и М2;
2) l=0, если точки М и М1 совпадают;
3) l< 0 в случае, если точка М лежит вне
отрезка М1М2;
4) Если М отлична от М1, то
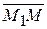 ¹-
¹- 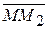 , следовательно, l¹-1 .
, следовательно, l¹-1 .
Наша задача заключается в том, чтобы найти координаты (x ; y) точки М, делящей отрезок М1М2 в заданном отношении l¹-1, если известны координаты (х1, у1) и (x 2 ; y 2) точек М1 и М2 .
Перепишем равенство (13) в координатной форме:
(х-х1; у-у1)=l(х2-х; y 2 -у), т.е. 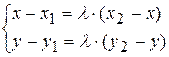 .
.
Решая первое уравнение относительно х, второе уравнение относительно у, получим (14) x = 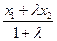 , y =
, y = 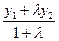 – координаты искомой точки М.
– координаты искомой точки М.
Формулы (14) называются формулами деления отрезка в данном отношении.
В частности, если l=1, т. е. если 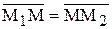 , точка М(х; у) является серединой отрезка М1М2. Формулы (14) примут вид x=
, точка М(х; у) является серединой отрезка М1М2. Формулы (14) примут вид x= 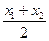 , y=
, y= 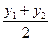 .
.
Следовательно, каждая координата середины отрезка равна полусумме соответствующих координат его концов.
Для нахождения координат точки М(х; у; z), делящей отрезок прямой пространства, определенного точками M1(x 1 ; y 1 ; z 1) и M2(x 2 ; y 2 ; z 2), в заданном отношении l, аналогичными рассуждениями получаем формулы
(15) x = 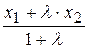 , y =
, y =  , z =
, z = 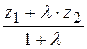 .
.
В частности, если точка М (х; у; z) делит отрезок М1М2 пополам, то l=1 и формулы (15) примут вид x = 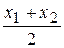 , y =
, y = 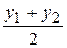 , z =
, z = 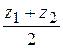 .
.
7.11 Перечисленные операции обобщаются и для векторов
с любым конечным числом переменных n :
пусть даны векторы 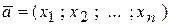 ,
, 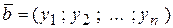 ,
,
тогда для них
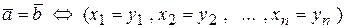 ,
,
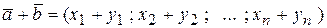 ,
,
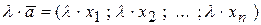 ,
,
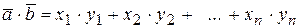 ,
,
Если 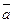 ¹0,
¹0, 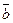 ¹0 и
¹0 и 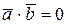 , то
, то  ^
^  ,
,
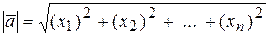 ,
, 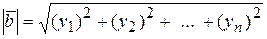 ,
,
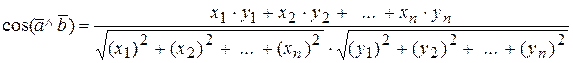 ,
, 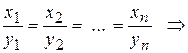 векторы
векторы 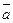 и
и 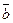 коллинеарны.
коллинеарны.
Для точек 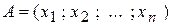 и
и 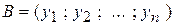
вектор 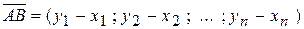 ,
,
расстояние |АB|= 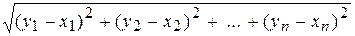 ,
,
середина 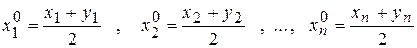 .
.
Все свойства перечисленных действий, рассмотренные ранее (не в координатной форме), сохраняются.
Пример 5
Даны векторы  = (1; 2; 3 ), =(1; -2; 0 ),
= (1; 2; 3 ), =(1; -2; 0 ), 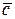 =(1; 2 ),
=(1; 2 ), 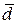 =(1; 2; 3),
=(1; 2; 3), 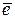 =(3; 2; 1) .
=(3; 2; 1) .
Для них 1) Перечислить равные векторы;
2) Найти 2×  –3
–3  +
+ 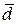 ;
;
3) Вычислить скалярное произведение векторов 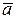 и
и 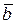 ;
;
4) Вычислить 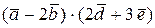 ;
;
5) Найти модули векторов  ,
,  ,
, 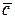 ;
;
6) Найти угол между  и
и  (в градусах и радианах).
(в градусах и радианах).
Решение:
1) Среди перечисленных векторов только одна пара совпадающих векторов:
 =
= 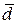 т.к. совпадают все соответствующие координаты ( 1=1, 2=2, 3=3),
т.к. совпадают все соответствующие координаты ( 1=1, 2=2, 3=3),
 ¹
¹  т.к. различны их вторые и третьи координаты (2¹-2, 3¹0 ),
т.к. различны их вторые и третьи координаты (2¹-2, 3¹0 ),
 ¹
¹ 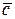 т.к. векторы имеют различные размерности и несравнимы;
т.к. векторы имеют различные размерности и несравнимы;
2) 2×  –3
–3  +
+ 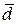 =2×(1; 2; 3) –3×(1; -2; 0) + (1; 2; 3 )=(2; 4; 6) – (3; -6; 0) +(1; 2; 3)=
=2×(1; 2; 3) –3×(1; -2; 0) + (1; 2; 3 )=(2; 4; 6) – (3; -6; 0) +(1; 2; 3)=
=(2 –3 + 1 ; 4 – (-6) +2; 6 – 0 +3)= (0; 12; 9),
2×  –3
–3  +
+ 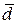 =(0; 12; 9);
=(0; 12; 9);
3)  ×
×  =(1; 2; 3)×(1; -2; 0)=1×1 + 2×(-2) + 3×0 =1 – 4 +0 = -3,
=(1; 2; 3)×(1; -2; 0)=1×1 + 2×(-2) + 3×0 =1 – 4 +0 = -3,
 ×
×  =3;
=3;
4) 1 способ:
 –2
–2  = (1; 2; 3) –2×(1; -2; 0) =(1–2; 2 + 4; 3–0)=(-1; 6; 3),
= (1; 2; 3) –2×(1; -2; 0) =(1–2; 2 + 4; 3–0)=(-1; 6; 3),
2 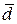 +3
+3 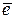 =2×(1; 2; 3)+3×(3; 2; 1)= (2+9; 4+6; 6+3)=(11; 10; 9),
=2×(1; 2; 3)+3×(3; 2; 1)= (2+9; 4+6; 6+3)=(11; 10; 9),
(  –2
–2  )×( 2
)×( 2 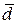 +3
+3 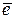 ) = (-1; 6; 3)×(11; 10; 9) = -1×11 + 6×10 + 3×9 = 76 ;
) = (-1; 6; 3)×(11; 10; 9) = -1×11 + 6×10 + 3×9 = 76 ;
2 способ:
(  –2
–2  )×( 2
)×( 2 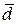 +3
+3 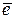 )=
)=  ×2
×2 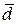 +
+  ×3
×3 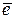 +(-2
+(-2  )×2
)×2 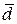 +(-2
+(-2  )×3
)×3 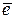 =
=
= 2×  ×
× 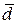 +3×
+3×  ×
× 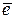 – 4×
– 4×  ×
× 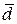 – 6×
– 6×  ×
× 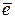 ,
,
 ×
× 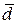 = (1; 2; 3)×(1; 2; 3) = 1×1 + 2×2 + 3×3 = 14,
= (1; 2; 3)×(1; 2; 3) = 1×1 + 2×2 + 3×3 = 14,
 ×
× 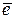 = (1; 2; 3)×(3; 2; 1) = 1×3 + 2×2 + 3×1 = 10,
= (1; 2; 3)×(3; 2; 1) = 1×3 + 2×2 + 3×1 = 10,
 ×
× 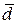 = (1; -2; 0)×(1; 2; 3) = 1×1 + (-2)×2 + 0×3= -3,
= (1; -2; 0)×(1; 2; 3) = 1×1 + (-2)×2 + 0×3= -3,
 ×
× 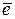 = (1; -2; 0)×(3; 2; 1) = 1×3 + (-2)×2 +0×1 = -1,
= (1; -2; 0)×(3; 2; 1) = 1×3 + (-2)×2 +0×1 = -1,
(  –2
–2  )×( 2
)×( 2 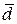 +3
+3 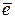 )= 2×14 + 3×10 –4×(-3) –6×(-1) = 28 + 30 +12 + 6 = 76 .
)= 2×14 + 3×10 –4×(-3) –6×(-1) = 28 + 30 +12 + 6 = 76 .
(  –2
–2  )×( 2
)×( 2 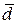 +3
+3 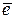 )=76 ;
)=76 ;
5) Модули векторов:
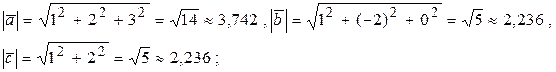
6) Косинус угла между векторами
cos ( 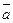 ^
^ 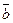 )=
)= 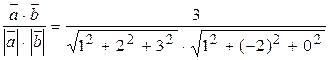 =
= 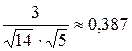 ,
,
( 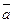 ^
^ 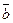 )= arccos(0,387)
)= arccos(0,387) 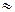 670 , в радианах (
670 , в радианах ( 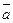 ^
^ 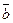 )=670
)=670 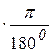
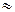 1,169.
1,169.
Пример 6
Даны точки пространства А(1; 2; 3) и В(4; -2; 1).
Найти координаты точек М1 – делящей отрезок АВ в отношении 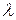 =0,4
=0,4
и М2 – середины отрезка АВ.
Решение:
Для нахождения координат точки М1 воспользуемся формулами (15)
x = 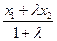 , y =
, y = 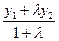 , z =
, z = 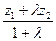 , которые при
, которые при 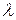 =0,4 примут вид
=0,4 примут вид
x = 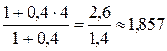 , y =
, y = 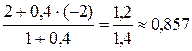 , z =
, z = 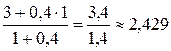 .
.
Получили точку М1(1,857; 0,857; 2,429).
Если точка М2 делит отрезок АВ пополам, то ее координаты найдутся как полусумма координат концов отрезка:
x= 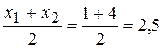 , y=
, y= 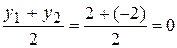 , z=
, z= 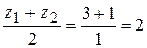 .
.
Получили точку М2(2,5; 0; 2).
Ответ: М1(1,857; 0,857; 2,429), М2 (2,5; 0; 2).
Векторное произведение
Дата: 2018-12-21, просмотров: 435.