11.2.7.1 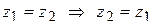 ;
;
11.2.7.2 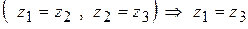 ;
;
11.2.7.3 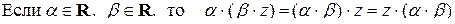 ;
;
11.2.7.4 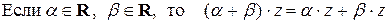 ;
;
11.2.7.5 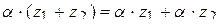 ;
;
11.2.7.6 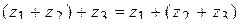 ;
;
11.2.7.7 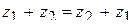 ;
;
11.2.7.8 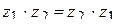 ;
;
11.2.7.9 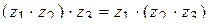 ;
;
11.2.7.10 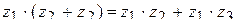 ,
,
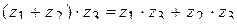 ;
;
11.2.7.11 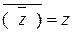 ;
;
11.2.7.12 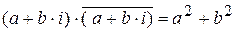 .
.
Доказательства перечисленных свойств вытекают из свойств операций с действительными числами и определений, доказывать не будем. Рекомендуем читателю попробывать свои силы в их доказательствах.
Пример 12
Выполнить действия:
1) Для 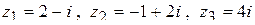 найти
найти 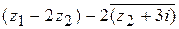 ;
;
2) Найти произведение (2-3i)×(-1+4i);
3) Найти произведение матриц с комплексными элементами
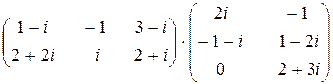 .
.
Решение:
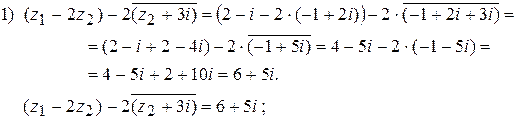
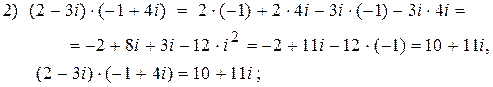
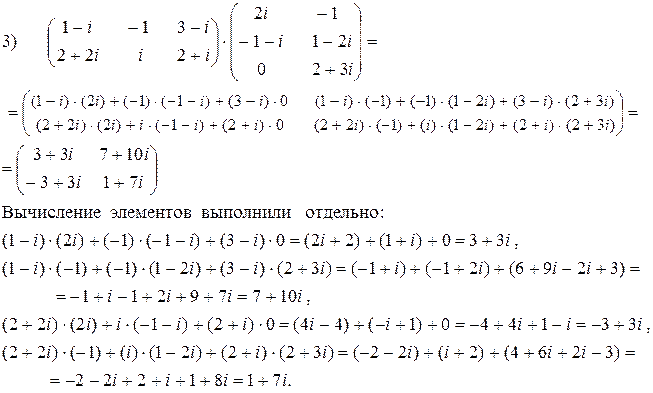 Пример 13
Пример 13
Найти 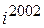 .
.
Решение: 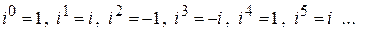 с периодом 4 порядка.
с периодом 4 порядка.
Тогда 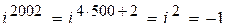 .
.
Ответ: -1.
11.3 Тригонометрическая и показательная формы
записи комплексного числа
Каждому действительному числу взаимооднозначно соответствует точка числовой прямой, множество действительных чисел одномерное.
Если мнимая часть комплексного числа ненулевая, то для его взаимооднозначного изображения недостаточно точек числовой прямой.
Для изображения комплексных чисел используется комплексная плоскость с декартовой системой координат: по оси абсцисс откладывают действительную часть Re(z) комплексного числа, по оси ординат откладывают мнимую часть Im(z) комплексного числа. Комплексное число однозначно задаёт точку плоскости и всякая точка плоскости с декартовыми координатами однозначно задаёт комплексное число.
На Рис.20 комплексные числа z1 =6+3i , z2 = –2+6i , z3= – 4i изображены точками комплексной плоскости.
Точка на плоскости может считаться также и конечной точкой радиус-вектора. Помимо декартовых координат точки (х; у) можно рассмотреть и её полярные координаты  , связь между ними описывается формулами (17), (18), (19).
, связь между ними описывается формулами (17), (18), (19).
Опр.28 Расстояние от начала координат до точки z=(a; b) называется модулем комплексного числа z и обозначается |z|. Угол между положительным направлением оси Re(z) и радиус-вектором, заданным точкой z=(a; b) (в направлении , противоположном движению часовой стрелки), называется аргументом числа z и обозначается Arg(z) или 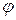 .
.
Модуль комплексного числа находится однозначно, но аргумент находится с точностью до угла, кратного 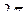 . Для удобства рассматривают основной аргумент arg(z), который отвечает условию
. Для удобства рассматривают основной аргумент arg(z), который отвечает условию 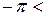 arg(z)
arg(z) 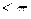 ,
,
тогда 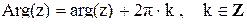 .
.
Пара чисел |z| и Arg(z) являются полярными координатами точки на комплексной плоскости, r = |z| и 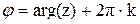 . Алгебраическая форма записи задаёт декартовы координаты той же точки.
. Алгебраическая форма записи задаёт декартовы координаты той же точки.
Получаем связь между декартовыми и полярными координатами:
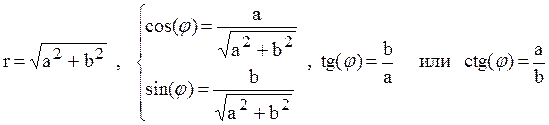 ,
,
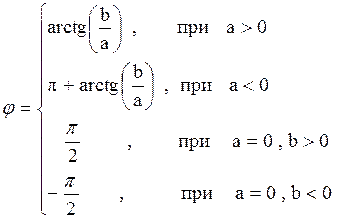 ,
,
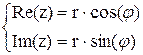 ,
,
z = a + b×i = r×cos( 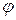 ) +r×sin(
) +r×sin( 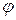 )× i .
)× i .
С учётом перечисленных формул получим
(21) z = |z|× ( cos( 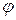 ) + i×sin(
) + i×sin( 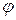 )) – тригонометрическая форма записи
)) – тригонометрическая форма записи
комплексного числа.
Эйлер вывел формулу, носящую его имя : 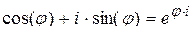 ,
,
применяя которую получим (22) 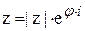 – показательная форма записи
– показательная форма записи
комплексного числа.
Пример 14
Записать в тригонометрической и показательной формах комплексные числа 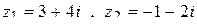 .
.
Записать в алгебраической форме 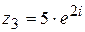 .
.
Изобразить  на комплексной плоскости.
на комплексной плоскости.
Решение:
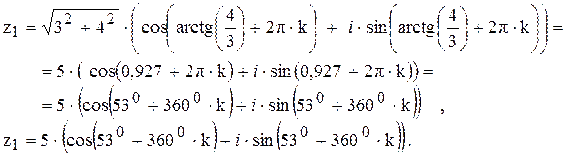
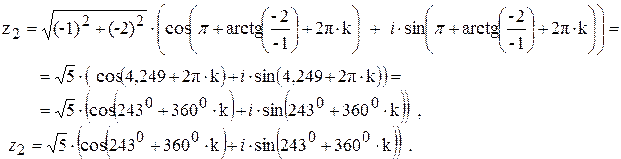
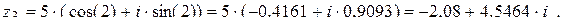
Дата: 2018-12-21, просмотров: 380.