1. В рамках Excel подготовим модель решения. Пусть N = 5. Разместим исходные данные задачи в первых трех строках электронной таблицы: ряд 0 1 2 3 4 5 в интервале ячеек В2: G2, ряд процентных ставок: 10% 20% 30% 40% 50% в интервале В3: G3.
| A | B | C | D | Е | F | G | |
| 1 | Последовательность процентных ставок | ||||||
| 2 | Срок | 0 | 1 | 2 | 3 | 4 | 5 |
| 3 | Процент | 0% | 10% | 20% | 30% | 40% | 50% |
Построим вычислительную схему. Объединим ячейки А4: G4 в одну и введем в нее текст Рекуррентная вычислительная схема решения, в ячейку А5 — текст Исходная сумма, в ячейку А6 — текст Доп. вклад, в ячейку А7 — текст Срок, в ячейку А8 — текст Проц. ставка, в ячейку А9 — текст Будущая стоимость. Скопируем интервал ячеек В2: G2 в интервал В7: G7, а интервал В3: G3 в интервал В8: G8.
Реализуем рекуррентное определение функции (3.2). В ячейку В9 введем формулу: =В5, в ячейку С9 — формулу:
=B9+($ B$5+$В$6*(В7-1))*B8+$В$6. Последнюю скопируем в интервал D9: G9.
Получим следующую модель решения.
| A | B | C | D | Е | F | G | |
| 4 | Рекуррентная вычислительная схема решения | ||||||
| 5 | Исходная сумма | ||||||
| 6 | Доп. вклад | ||||||
| 7 | Срок | 0 | 1 | 2 | 3 | 4 | 5 |
| 8 | Процентная ставка | 0% | 10% | 20% | 30% | 40% | 50% |
| 9 | Будущая стоимость | <Формула> | <Формула> | —"— | —"— | —"— | —"— |


2. Введем конкретные значения остальных параметров задачи. В ячейку В5 введем P0 = 1000, ячейку В6 — значение дополнительного вклада (значение A = 40).
В результате получим решение задачи в следующем виде.
| A | B | C | D | Е | F | G | |
| 4 | Рекуррентная вычислительная схема решения | ||||||
| 5 | Исходная сумма | 1000 | |||||
| 6 | Доп. вклад | 40 | |||||
| 7 | Срок | 0 | 1 | 2 | 3 | 4 | 5 |
| 8 | Проц. ставка | 0% | 10% | 20% | 30% | 40% | 50% |
| 9 | Будущая стоимость | 1000 | 1140 | 1388 | 1752 | 2240 | 2860 |
Второй способ решения
1. В рамках Excel подготовим модель решения. Обычным образом введем текстовые данные, скопируем ряды 0 1 2 3 4 5 и 0% 10% 20% 30% 40% 50%. В интервал А8:А13 последний ряд вставим с использованием команды Специальная вставка (см. п. 3.1.7 "Копирование рядов"). Ряд из одинаковых значений 40 построим так: выделим интервал В9:В13, введем 40, нажмем Ctrl + Enter. В ячейку В8 введем формулу: =В5, в ячейку С8 — формулу: =$B8*(1+СУММ($С$7:С$7)--СУММ($А$8:$А8)). Завершив формирование модели решения аналогично рассмотренному выше (см. задача 1, второй способ), получим следующую модель решения.
| A | B | C | D | Е | F | G | H | |
| 4 | Вычислительная схема решения специального вида | |||||||
| 5 | Исходная сумма | |||||||
| 6 | Срок | 0 | 1 | 2 | 3 | 4 | 5 | |
| 7 | Процентная ставка | Вклады | 0% | 10% | 20% | 30% | 40% | 50% |
| 8 | 0% | —"— | —"— | —"— | —"— | —"— | ||
| 9 | 10% | 40 | —"— | —"— | —"— | —"— | —"— | |
| 10 | 20% | 40 | —"— | —"— | —"— | —"— | ||
| 11 | 30% | 40 | —"— | —"— | —"— | |||
| 12 | 40% | 40 | —"— | —"— | ||||
| 13 | 50% | 40 | —"— | |||||
| 14 | Буд. стоимость | |||||||


2. Введем конкретные значения остальных параметров задачи. В ячейку В5 введем P0 = 1000.
| A | B | C | D | Е | F | G | H | |
| 4 | Вычислительная схема решения специального вида | |||||||
| 5 | Исходная сумма | 1000 | ||||||
| 6 | Срок | 0 | 1 | 2 | 3 | 4 | 5 | |
| 7 | Процентная ставка | Вклады | 0% | 10% | 20% | 30% | 40% | 50% |
| 8 | 0% | 1000 | 1000 | 1100 | 1300 | 1600 | 2000 | 2500 |
| 9 | 10% | 40 | 40 | 48 | 60 | 76 | 96 | |
| 10 | 20% | 40 | 40 | 52 | 68 | 88 | ||
| 11 | 30% | 40 | 40 | 56 | 76 | |||
| 12 | 40% | 40 | 40 | 60 | ||||
| 13 | 50% | 40 | 40 | |||||
| 14 | Буд. стоимость | 1000 | 1140 | 1388 | 1752 | 2240 | 2860 | |
Задача 3. Определить ряд сумм, образующихся на депозитном счете в банке, на конец каждого из N месяцев при условиях: 1) в начале первого месяца на счет была положена сумма P0, а в конце каждого из N месяцев — соответственно суммы A1, ..., AN, 2) месячная процентная ставка нефиксированная и составляет pi% в i-ом месяце.
Требуется:
1. Разработать компьютерную модель решения задачи.
2. Ввести конкретные значения параметров и решить задачу.
Первый способ решения
Математические основы решения задачи. Рассматриваемая задача представляет собой общий случай подобных задач. В общем случае имеем следующее выражения для будущей стоимости (cм. задачу 2 текущей лабораторной работы):
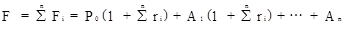
Непосредственное построение такой формулы в рамках Excel затруднительно, поэтому удобнее пользоваться рекуррентным определением:
(3.3)
Дата: 2018-11-18, просмотров: 380.