Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

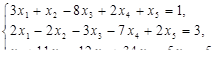
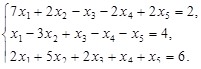
Решить задачи линейного программирования

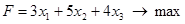, при ограничениях

   

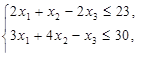
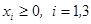
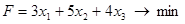, при ограничениях

     

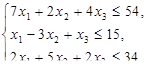
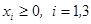
Вариант 2

Решить уравнения

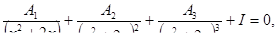
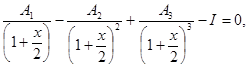
Решить системы линейных уравнений

        

 

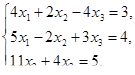
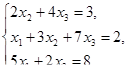
Решить задачи линейного программирования

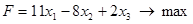, при ограничениях

    

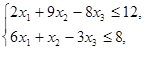
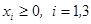
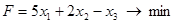, при ограничениях

   

 

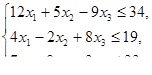
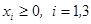
Вариант 3

Решить уравнения

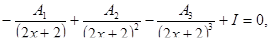
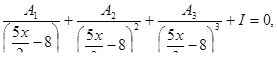
Решить системы линейных уравнений

        

 

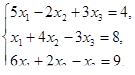
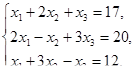
Решить задачи линейного программирования

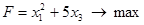, при ограничениях

     

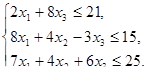
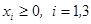
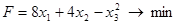, при ограничениях

     

 

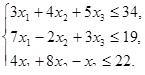
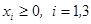
Вариант 4

Решить уравнения

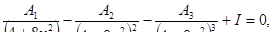
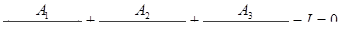
Решить системы линейных уравнений

    

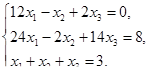
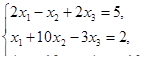
Решить задачи линейного программирования

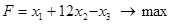, при ограничениях

     

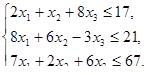
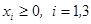
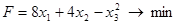, при ограничениях

           

 

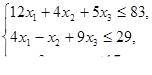
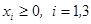
Вариант 5

Решить уравнения

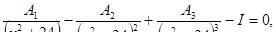
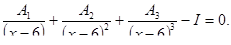
Решить системы линейных уравнений

 

 

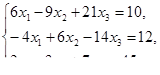
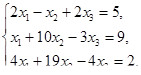
Решить задачи линейного программирования

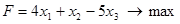, при ограничениях

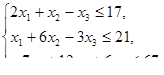
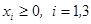
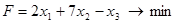, при ограничениях

 

 

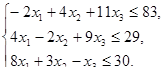
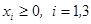
Вариант 6

Решить уравнения

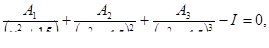
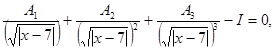
Решить системы линейных уравнений

      

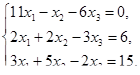
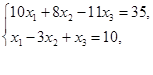
Решить задачи линейного программирования

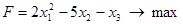, при ограничениях

      

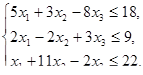
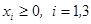
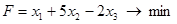, при ограничениях

      

 

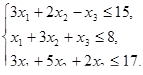
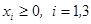
Вариант 7

Решить уравнения

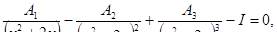
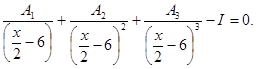
Решить системы линейных уравнений

     

 

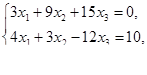
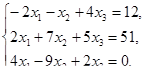
Решить задачи линейного программирования

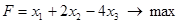, при ограничениях

   

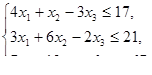
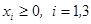
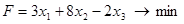, при ограничениях

  

 

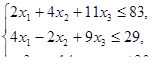
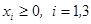
Вариант 8

Решить уравнения

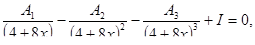
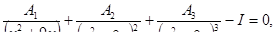
Решить системы линейных уравнений

    

 

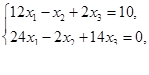
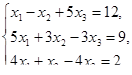
Решить задачи линейного программирования

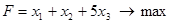, при ограничениях

     

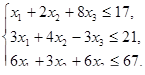
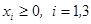
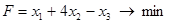, при ограничениях

    

 

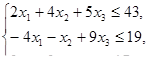
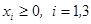
Вариант 9

Решить уравнения

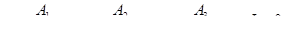
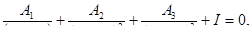
Решить системы линейных уравнений

      

 

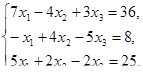
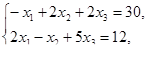
Решить задачи линейного программирования

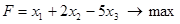, при ограничениях

      

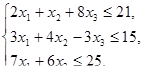
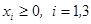
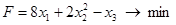, при ограничениях           

       

 

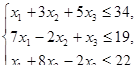
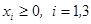
Вариант 10

Решить уравнения

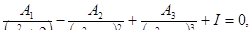
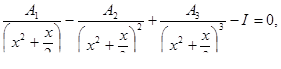
Решить системы линейных уравнений

      

 

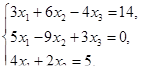
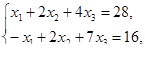
Решить задачи линейного программирования

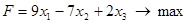, при ограничениях

   

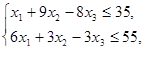
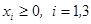
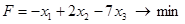, при ограничениях

     

 

 

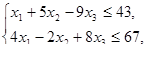
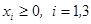
Лабораторная работа №14

Специальные приемы решение задач (рекурсия и построение
вычислительных схем специального вида)

Цель работы. Изучение технологии построения компьютерных моделей с использованием рекуррентного определения функции и приобретение практических навыков построения специфических вычислительных схем.

Содержание

Изучаются вопросы:

1. Понятие рекуррентного определения функции

2. Технология построения компьютерных моделей с использованием рекуррентного определения функции.

Выполняется вариант задания.

Указания

Пусть требуется решить следующие задачи.

Задача 1. Определить ряд сумм, образующихся на депозитном счете в банке, на конец каждого из N месяцев при условиях: 1) в начале первого месяца на счет была положена сумма P₀, а в конце каждого из N месяцев — соответственно суммы A₁, ..., A_N, 2) месячная процентная ставка фиксированная и составляет p%, 3) начисление идет по схеме простых процентов.

Требуется:

1. Разработать компьютерные модели решения задачи.

2. Ввести конкретные значения параметров и решить задачу.

Первый способ решения

Математические основы решения задачи. Математическая модель наращения по простому проценту при фиксированной процентной ставке и однократном вложении средств общеизвестна и представляет собой выражение вида:

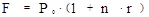.                                               (3.1)

Исходя из условия задачи, имеем следующие равенства:

,

,

..............…………………………...

,

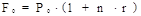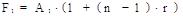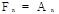где F₀ — будущая стоимость начальной суммы P₀, F_k — будущая стоимость суммы A_k на конец n–го интервала начисления процентов.

Следовательно,

.

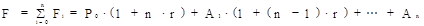Реализовать такую функцию в Excel непосредственно затруднительно, поскольку с увеличением N (срока) увеличивается количество слагаемых, т.е. для каждого следующего значения N требуется добавлять в формулу еще одно слагаемое. Автоматизировать такой процесс можно только с помощью рекуррентного определения функции.

Рекуррентное определение функции F имеет вид:

 

 

(3.2)