1. В рамках Excel подготовим модель решения. В ячейку А1 введем текст Исходная сумма, в ячейку А2 — текст Проц. ставка, в ячейку А3 — текст Срок, в ячейку А4 — Доп. вклады, в ячейку А5 — Буд. стоимость. Построим последовательность 0 1 2 3 4 5 в интервале В3: G3 и последовательность вкладов 40 50 60 70 80 в интервале С4: G4. Реализуем рекуррентную схему определения функции (3.2), задающую будущую стоимость: в ячейку В5 введем формулу =В1, в ячейку С5 — формулу вида:=В5 + ($В$1 + СУММ($В$4:В4))*$ B$2 + С4. Последнюю формулу скопируем в интервал D5: G5.
В результате получим следующую модель решения.
| A | B | C | D | Е | F | G | |
| 1 | Исходная сумма | ||||||
| 2 | Проц. ставка | ||||||
| 3 | Срок | 0 | 1 | 2 | 3 | 4 | 5 |
| 4 | Доп. вклады | 40 | 50 | 60 | 70 | 80 | |
| 5 | Буд. стоимость | —"— | —"— | —"— | —"— |


2. Введем конкретные значения параметров задачи. В ячейку В1 введем значение Р0 = 1000, в ячейку В2 — значение р = 10%.
В результате получим решение задачи в следующем виде.
| A | B | C | D | Е | F | G | |
| 1 | Исходная сумма | 1000 | |||||
| 2 | Проц. ставка | 10% | |||||
| 3 | Срок | 0 | 1 | 2 | 3 | 4 | 5 |
| 4 | Доп. вклады | 1000 | 40 | 50 | 60 | 70 | 80 |
| 5 | Буд. стоимость | 1000 | 1140 | 1294 | 1463 | 1648 | 1850 |
Второй способ решения
1. В рамках Excel подготовим модель решения. Положим N = 4, P0 = 1000 и значения дополнительных вкладов в виде последовательности: 30 40 50 60. Объединим ячейки А1: G1 в одну и введем в нее текст Вычислительная схема решения специального вида, в ячейку А2 — текст Проц. ставка, в ячейку А3 — текст Срок, в ячейку А9 — текст Буд. стоимость. Построим в интервалах ячеек С3: G3 и А4:А8 последовательность: 0 1 2 3 4, в интервале ячеек В4:В8 последовательность: 1000 30 40 50 60.
В ячейку С4 введем формулу вида (3.1) в алфавите языка формул Excel специального вида: =$B4*(1+(С$3-$А4)*$B$2) и скопируем ее последовательно в ячейки D5, E6, F7 и G8.
Скопируем формулы, полученные в ячейках С4, D5, E6, F7 и G8, с использованием Автозаполнителя соответственно в интервалы ячеек: D4: G4; E5: G5; F6: G6, G7: G7.
Построим в ячейке C9 формулу суммирования содержимого интервала ячеек С4:С8 вида: =СУММ(С4:С8), затем скопируем ее в интервал D9: G9.
Получим следующую модель решения.
| A | B | C | D | Е | F | G | |
| 1 | Вычислительная схема решения специального вида | ||||||
| 2 | Проц. ставка | ||||||
| 3 | Срок | 0 | 1 | 2 | 3 | 4 | |
| 4 | 0 | 1000 | <Формула> | —"— | —"— | —"— | —"— |
| 5 | 1 | 30 | —"— | —"— | —"— | —"— | |
| 6 | 2 | 40 | —"— | —"— | —"— | ||
| 7 | 3 | 50 | —"— | —"— | |||
| 8 | 4 | 60 | —"— | ||||
 9 9
| Буд. стоимость | <Формула> | —"— | —"— | —"— | —"— | |

2. Введем конкретные значения параметров задачи. В ячейку В2 — значение р = 10%.
В результате получим решение задачи в следующем виде.
| A | B | C | D | Е | F | G | |
| 1 | Вычислительная схема решения специального вида | ||||||
| 2 | Проц. ставка | 10% | |||||
| 3 | Срок | 0 | 1 | 2 | 3 | 4 | |
| 4 | 0 | 1000 | 1000 | 1100 | 1200 | 1300 | 1400 |
| 5 | 1 | 30 | 30 | 33 | 36 | 39 | |
| 6 | 2 | 40 | 40 | 44 | 48 | ||
| 7 | 3 | 50 | 50 | 55 | |||
| 8 | 4 | 60 | 60 | ||||
| 9 | Буд. стоимость | 1000 | 1130 | 1273 | 1430 | 1602 | |
Задача 2. Определить ряд сумм, образующихся на депозитном счете в банке, на конец каждого из N месяцев при условиях: 1) в начале первого месяца на счет была положена сумма P0, а в конце каждого из N месяцев — одна и та же сумма, равная А, 2) месячная процентная ставка нефиксированная и составляет pi% в i-ом месяце, 3) начисление идет по схеме простых процентов.
Первый способ решения
Математические основы решения задачи. Исходя из условия задачи, в общем случае имеем следующие соотношения:
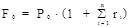 ,
,
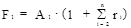 ,
,
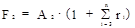 ,
,
.....................
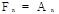 .
.
Отсюда получаем:
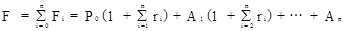 .
.
При условии A1 = A2 =...= An = А имеем:
 .
.
Непосредственное построение такой формулы в рамках Excel затрудненно, поэтому удобнее пользоваться рекуррентным определением:

(3.2)
Дата: 2018-11-18, просмотров: 393.