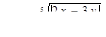для 6 значений x: x1 = 0,2; шаг h = 0,7.
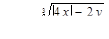для 7 значений у: у1 = 1,5; шаг h = 0,3.
Табулировать функции по двум аргументам
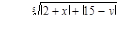для 5 значений x: x 1 = 2,2; шаг h = 0,8 и 5 значений y: y1 = 1,5; шаг h = 0,4.
Вычислить значения выражений
, 
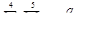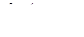
Вариант 2
Табулировать функции по одному аргументу
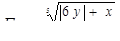для 5 значений x: x1 = 2,1; шаг h = 0,3.
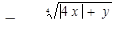для 6 значений у: у1 = 2,1; шаг h = 0,3.
Табулировать функции по двум аргументам
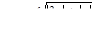для 5 значений x: x 1 = 1,7; шаг h = 0,5 и 5 значений y: y1 = 4; шаг h = 0,2.
Вычислить значения выражений
, 
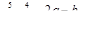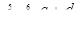
Вариант 3
Табулировать функции по одному аргументу
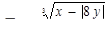для 5 значений x: x1 = 0,3; шаг h = 0,5.
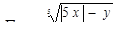для 5 значений у: у1 = 1,2; шаг h = 0,2.
Табулировать функции по двум аргументам
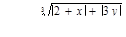для 4 значений x: x 1 = 2,3; шаг h = 0,5 и 5 значений y: y1 = 1; шаг h = 0,3.
Вычислить значения выражений
, 
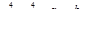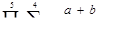
Вариант 4
Табулировать функции по одному аргументу
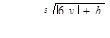для 7 значений x: x1 = 2,6; шаг h = 0,4.
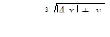для 5 значений у: у1 = 1,3; шаг h = 0,3.
Табулировать функции по двум аргументам
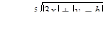для 4 значений x: x 1 = 1,4; шаг h = 0,5 и 5 значений y: y1 = 1,2; шаг h = 0,7.
Вычислить значения выражений
, 
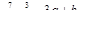Вариант 5
Табулировать функции по одному аргументу
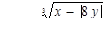для 5 значений x: x1 = 0,3; шаг h = 0,5.
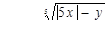для 5 значений у: у1 = 1,2; шаг h = 0,2.
Табулировать функции по двум аргументам
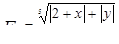для 4 значений x: x 1 = 1,2; шаг h = 0,7 и 5 значений y: y1 = 1; шаг h = 0,2.
Вычислить значения выражений
, 
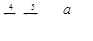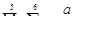
Вариант 6
Табулировать функции по одному аргументу
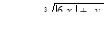для 4 значений x: x1 = 2,3; шаг h = 0,4.
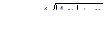для 5 значений у: у1 = 1,7; шаг h = 0,3.
Табулировать функции по двум аргументам
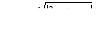для 5 значений x: x 1 = 1,4; шаг h = 0,7 и 6 значений y: y1 = 2; шаг h = 0,4.
Вычислить значения выражений
, 
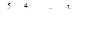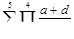
Вариант 7
Табулировать функции по одному аргументу
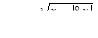для 4 значений x: x1 = 0,5; шаг h = 0,5.
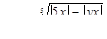для 5 значений у: у1 = 2,2; шаг h = 0,4.
Табулировать функции по двум аргументам
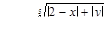для 6 значений x: x 1 = 1,8; шаг h = 0,8 и 5 значений y: y1 = 3; шаг h = 0,2.
Вычислить значения выражений
, 
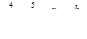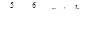
Вариант 8
Табулировать функции по одному аргументу
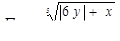для 5 значений x: x1 = 1,3; шаг h = 0,6.
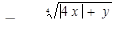для 6 значений у: у1 = 1,2; шаг h = 0,2.
Табулировать функции по двум аргументам
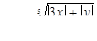для 4 значений x: x 1 = 1,3; шаг h = 0,6 и 5 значений y: y1 = 1; шаг h = 0,5.
Вычислить значения выражений
, 
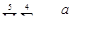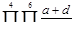
Вариант 9
Табулировать функции по одному аргументу
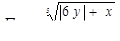для 5 значений x: x1 = 1,3; шаг h = 0,6.
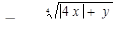для 6 значений у: у1 = 1,2; шаг h = 0,2.
Табулировать функции по двум аргументам
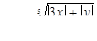для 4 значений x: x 1 = 1,3; шаг h = 0,6 и 5 значений y: y1 = 1; шаг h = 0,5.
Вычислить значения выражений
, 
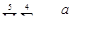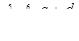
Вариант 10
Табулировать функции по одному аргументу
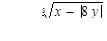для 5 значений x: x1 = 0,3; шаг h = 0,5.
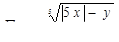для 5 значений у: у1 = 1,2; шаг h = 0,2.
Табулировать функции по двум аргументам
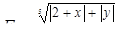для 4 значений x: x 1 = 1,3; шаг h = 0,6 и 5 значений y: y1 = 1; шаг h = 0,5.
Вычислить значения выражений
, 
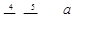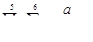
Лабораторная работа №13
Методы решения задач "Подбор параметра" и "Поиск решения"
Цель работы. Изучение технологии построения компьютерных моделей с использованием методов "Подбор параметра", "Поиск решения" и приобретение практических навыков построения вычислительных схем.
Содержание
Изучаются вопросы:
1. Метод решения задач "Подбор параметра".
2. Метод решения задач "Поиск решения".
Выполняется вариант задания.
Указания
Использование средства "Подбор параметра"
При решении задач часто возникает необходимость определить, какими должны быть исходные данные, чтобы получить известный результат. Например, требуется определить, каким должен быть размер первоначального вклада в банк, чтобы через известное время получить на счете заданную сумму при неизменной процентной ставке и начислении по схеме простых процентов.
Для решения подобных задач Excel располагает средством, называемым Подбор параметра.
Общая постановка задач, решаемых указанным средством, может заключаться в следующем. Требуется определить неизвестное X из соотношения F ( A , X , Y , Z ) = B , при известных значениях A , Y , Z и B .
Вычислительная схема решения этого уравнения рассматриваемым методом имеет вид.
| A | B | C | D | |
| 1 | Значение A | <число> | ||
| 2 | Значение X | |||
| 3 | Значение Y | <число> | ||
| 4 | Значение Z | <число> | ||
| 5 | Значение В | <число> | ||
| 6 | Значение функции | <Формула> |
Построение этой схемы решения заключается в следующем. Резервируются две ячейки для ввода значений параметров уравнения A (ячейка В1) и B (ячейка В5) , три ячейки для значений аргументов X,Y,Z (соответственно ячейки В2, В3, В4) и одна ячейка для ввода собственно левой части уравнения (ячейка В6).
Следует заметить, что ячейка для значения X (ячейка В2) оставляется пустой, поскольку именно в нее Excel будет помещать результат, т.е. решение заданного уравнения.
Затем выполняется следующая последовательность действий: меню Сервис Þ команда Подбор параметра. В окне диалога Подбор параметра в поле ввода Установить в ячейке вводится ссылка на ячейку В6, в поле ввода Значение вводится значение В (число, а не ссылка), в поле ввода Изменяя ячейку вводится ссылка на ячейку В2.
Аналогично можно решать уравнения относительно другой переменной Y, Z (но только одной) — изменяются лишь ссылки на ячейки в поле ввода Изменяя ячейку.
Отметим некоторые особенности решения задач с использованием средства Подбор параметра. Как правило, оно выдает точные ответы. Однако в некоторых, даже простых, ситуациях это средство может не дать желаемого результата. Причина этого заключается в том, что по умолчанию средство Подбор параметра производит 100 попыток найти ответ, причем поиск прекращается, когда найден ответ с точностью до 0,001. Для получения точного результата в этом случае требуется изменить количество итераций или уменьшить относительную погрешность вычислений (меню Сервис Þ команда Параметры вкладка Вычисления).
Использование средства "Поиск решения"
Средство Поиск решения представляет собой мощный инструмент решения таких задач, которые удовлетворяют следующим критериям:
§ цель (результат) задачи определяется как достижение определенного, максимального или минимального значения для некоторой функции, т.е. решение задач вида F(A,X,Y,Z) = В или F(A,X,Y,Z) ® extr(min,max);
§ на аргументы и параметры функции накладываются определенные ограничения в виде системы линейных или нелинейных равенств (неравенств).
 |
Рассмотрим применение указанного средства для решения системы линейных уравнений.
Пусть задана система линейных уравнений вида:
Примем первое уравнение за функцию цели, которую для данной задачи требуется установить равной значению b1. Остальные уравнения системы примем за систему ограничений.
Таким образом, задача сформулирована для решения средством Поиск решения.
Подготовим вычислительную схему решения. Зарезервируем три ячейки для решения системы (интервал В1:В3) и для их интерпретаций (интервал А1:А3). В ячейку В4 введем левую часть первого уравнения: = a 11 * B 1+ a 12 * B 2+ + a 13 * B 3; в ячейку В5 — левую часть второго уравнения: = a 21 * B 1+ a 22 * B 2+ a 23 * B 3; в ячейку В6 — левую часть третьего уравнения: = a 21 * B 1+ a 22 * B 2+ a 23 * B 3. Здесь аij — числа, используемые непосредственно в формулах, хотя для обеспечения большей гибкости вычислительной схемы для них можно было бы зарезервировать ячейки; B 1, B 2, B 3 — ссылки на ячейки, зарезервированные для x1, x2, x3.
Окончательно вычислительная схема принимает следующий вид:
| A | B | C | D | |
| 1 | Значение x1 | |||
| 2 | Значение x2 | |||
| 3 | Значение x3 | |||
| 4 | Первое уравнение | <Формула> | ||
| 5 | Второе уравнение | <Формула> | ||
| 6 | Третье уравнение | <Формула> |
Завершив формирование схемы вычисления, запускаем средство Поиск решения последовательностью действий: меню Сервис Þ команда Поиск решения. В появляющемся диалоговом окне Поиск решения (Рис.3.2) необходимо сделать следующие установки.
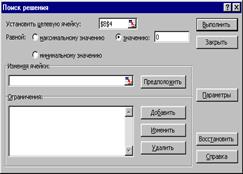
Рис. 3.2. Диалоговое окно Поиск решения.
В поле Установить целевую ячейку ввести ссылку на ячейку В4, в разделе Равной в поле Значению ввести значение b1, в поле Изменяя ячейки ввести ссылки на ячейки В1:В3 (ячейки, зарезервированные для значений неизвестных). Для того чтобы сформировать ограничения, в разделе Ограничения нажимается кнопка Добавить…, в появляющемся диалоговом окне Добавить ограничение (Рис. 3.3) формулируются ограничения следующим образом: в поле Ссылка на ячейку вносится ссылка на ячейку, в которой расположено второе уравнение системы (ячейка В5), в поле Ограничение, состоящее из двух элементов вначале выбирается из списка знак отношения ‘= ‘, затем вводится значение b2. В окне Добавить ограничение нажимается кнопка Добавить. Аналогичным образом строится второе ограничение.
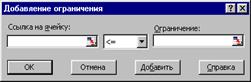
Рис. 3.2. Диалоговое окно Добавить ограничения.
После ввода ограничений диалоговое окно Добавить ограничение закрывается кнопкой ОК и происходит возврат к окну Поиск решения.
При этом в поле ввода раздела Ограничение появляются сформированные ограничения. Воспользовавшись кнопками Изменить и Удалить, можно скорректировать либо удалить любое ограничение.
Теперь все параметры средства Поиск решения заданы, и его можно запустить в работу. Для этого необходимо в диалоговом окне Поиск решения нажать кнопку Выполнить.
После завершения работы средства Поиск решения в ячейках, зарезервированных для значений неизвестных, сформируется решение системы линейных уравнений, а на экране появится диалоговое окно Результаты поиска решения, содержащее информацию об окончании процесса поиска решения. Для того, чтобы найденные решения занеслись в зарезервированные для них ячейки, необходимо установить флажок Сохранить найденное решение. Кроме того, по результатам решения можно создать отчет и сценарий из найденных значений неизвестных.
Решение задачи линейного программирования. Задача линейного программирования формулируется следующим образом: найти такие значения неизвестных x1, x2, x3, которые максимизируют линейную форму F при заданных линейных ограничениях.
Рассмотрим пример. Пусть требуется решить следующую задачу линейного программирования:
,
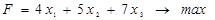при линейных ограничениях:
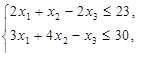
Подготовим вычислительную схему решения. Зарезервируем три ячейки для решения задачи (интервал В1:В3) и для их интерпретаций (интервал А1:А3). В ячейку В4 введем формулу, определяющую линейную форму, которую требуется максимизировать: =4* B 1 + 5* B 2 + 7* B 3; в ячейку В5 — левую часть первого ограничения: =2* B 1 + B 2 -- 2* B 3; в ячейку В6 — левую часть второго ограничения: =3* B 1 + 4* B 2 - B 3, в ячейку В7 — левую часть третьего ограничения: =2* B 1 + 11* B 2 + 2* B 3.
В ячейки А4:А7 введем соответствующие интерпретации для ограничений системы.
Окончательно вычислительная схема решения принимает следующий вид:
| A | B | C | D | |
| 1 | Значение x1 | |||
| 2 | Значение x2 | |||
| 3 | Значение x3 | |||
| 4 | Линейная форма F | <Формула> | ||
| 5 | Первое ограничение | <Формула> | ||
| 6 | Второе ограничение | <Формула> | ||
| 7 | Третье ограничение | <Формула> |
 |  |
Завершив формирование схемы вычисления, запускаем средство Поиск решения. В появляющемся диалоговом окне Поиск решения (Рис.3.2) производятся установки.
В поле Установить целевую ячейку требуется ввести ссылку на ячейку В4, в разделе Равной установить флажок максимальному значению, в поле Изменяя ячейки ввести ссылки на ячейки В1:В3 (ячейки, зарезервированные для значений неизвестных).
Формирование системы линейных ограничений проводят аналогично изложенному выше.
Задав все параметры средства Поиск решения, требуется нажать кнопку Выполнить для того, чтобы запустить его в работу.
После завершения работы средства Поиск решения в ячейках, зарезервированных для значений неизвестных, сформируется решение задачи линейного программирования.
Задания
Вариант 1
Решить уравнения
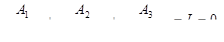
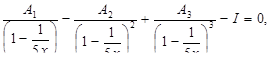
Дата: 2018-11-18, просмотров: 414.
