Дифференциальные уравнения второго порядка в общем случае имеют вид:  .
.
Дифференциальные уравнения вида y ″ = f ( x ) решаются двукратным интегрированием.
Полагая y ′ = z, имеем y ″ = z ′ или z ′ = f ( x ) , 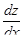 = f ( x ), dz = f ( x ) dx .
= f ( x ), dz = f ( x ) dx .
Интегрируя 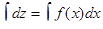 , получим z = F ( x ) + C 1.
, получим z = F ( x ) + C 1.
Возвращаясь к функции y , имеем 
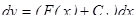 ,
,  .
.
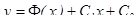 - это есть общее решение уравнения
- это есть общее решение уравнения
y ″ = f ( x ).
Пример 1: Найти общее решение уравнения 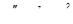 .
.
Решение: Пусть 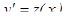 , тогда
, тогда  .
.
После подстановки имеем 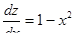 или
или 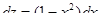 .
.
Интегрируя обе части равенства, получим 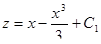 .
.
Вернувшись к функции y , получаем уравнение  .
.
Интегрируя его 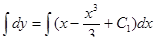 , получим
, получим 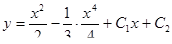 -это есть общее решение уравнения.
-это есть общее решение уравнения.
Ответ: 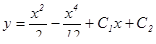 .
.
Линейные однородные дифференциальные уравнения
Второго порядка с постоянными коэффициентами
Определение: Уравнения вида 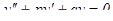 , где p и q– постоянные величины, называются линейными однородными дифференциальными уравнениями второго порядка с постоянными коэффициентами.
, где p и q– постоянные величины, называются линейными однородными дифференциальными уравнениями второго порядка с постоянными коэффициентами.
Для отыскания общего решения такого уравнения составляется характеристическое уравнение 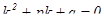 ,
,
которое решается как квадратное уравнение. При его составлении в исходном уравнении производные функции y заменяются соответствующей степенью переменной k, причем сама функция y заменяется единицей.
Общее решение исходного дифференциального уравнения строится в зависимости от характера корней 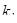 и
и  .
.
Возможны три случая:
1) 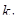 и
и  – действительные и различные, тогда
– действительные и различные, тогда
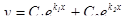 ;
;
2) 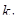 и
и  – действительные и равные, тогда
– действительные и равные, тогда 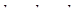 и
и
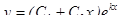 ;
;
3) 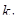 и
и  – комплексно-сопряженные:
– комплексно-сопряженные:  ,
,  ,
,
тогда 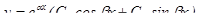 .
.
Пример1: Решить дифференциальное уравнение
y˝- 5y΄- 6y = 0.
Решение: Заменим данное уравнение характеристическим:
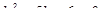 .
.
решаем его, получаем  .
.
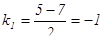 ,
, 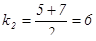 .
.
Как видно, корни действительные и различные , поэтому
общее решение можно записать в виде 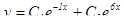 .
.
Ответ: 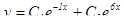 .
.
Пример 2: Решить дифференциальное уравнение  .
.
Решение: Заменим данное уравнение характеристическим
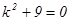 , найдем корни ,
, найдем корни ,  , значит
, значит 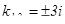 .
.
Отсюда действительная частькомплексного числа 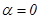 , мнимая часть
, мнимая часть 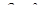 , следовательно общее решение имеет вид:
, следовательно общее решение имеет вид:
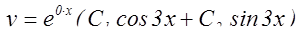 .
.
Ответ: 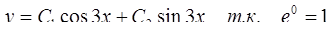
Пример 3: Решить дифференциальное уравнение
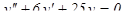 .
.
Решение: Заменим данное уравнение характеристическим:
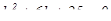 .
.
Решая его, получаем 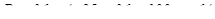 ;
;
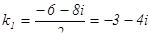 ,
, 
получили комплексно - сопряженные корни, где  и
и  . Тогда общее решение запишется в виде
. Тогда общее решение запишется в виде 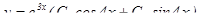 .
.
Ответ: 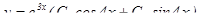
Пример 4: Решить дифференциальное уравнение
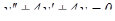 .
.
Решение: Заменим данное уравнение характеристическим:
 .
.
Решая его, получаем  ;
;
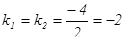 ,
,
получили два одинаковых действительных корня, тогда
общее решение уравнения запишется в виде 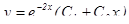 .
.
Ответ: 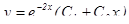 .
.
Линейные однородные
Определение.Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида
y″ + py′ + qy = f ( x ),
где p и q – постоянные величины, а f(x) – непрерывная функция x.
Если правая часть уравнения равна нулю, т.е.
y″ + py′ + qy = 0,
то оно называется однородным уравнением.
Для практического использования алгоритм решениядифференциальных уравнений второго порядка с постоянными коэффициентамиудобно оформить в виде таблицы:
| Дифференциальное уравнение |
y″ + py′ + qy = 0 | ||
| Характеристическое уравнение |
k2 + pk + q = 0
| ||
| Дискриминант D = p2 – 4q | D > 0 | D = 0 | D < 0 |
| Корни характеристического уравнения | k1 ≠ k2 | k1 = k2 | k1 = a + bi k2 = a - bi |
| Множества решений |
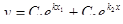
|
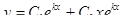
|

|
Пример.Решить уравнение y″ + 2y′ – 8y = 0.
Решение.
Составим характеристическое уравнение k2 + 2k - 8 = 0.
Найдем дискриминант D = p2 – 4q = 22 -4(-8) = 4 + 32 = 36 > 0.
Следовательно, характеристическое уравнение имеет два различных действительных корня. Определим их: k1 = - 4, k2 = 2.
Находим частные решения данного дифференциального уравнения:
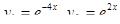 .
.
Общее решение данного уравнения имеет вид
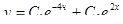 .
.
ЗАДАНИЯ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ
Вариант 1
Найти общее решение дифференциального уравнения
1. y′ = 6x3;
2. y′′ + y′ – 6y = 0
3. 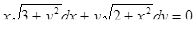 4.
4. 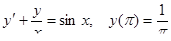 5.
5. 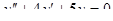
|
Вариант 2
Найти общее решение дифференциального уравнения
1. y′ = 8x2 ;
2. y′′ – 6y + 9 = 0
3. 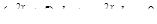 4.
4. 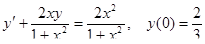 5.
5. 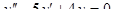
|
Вариант 3
Найти общее решение дифференциального уравнения
1. y′ = 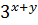 ;
2. y′′ – 2y′ – 8y = 0.
3. ;
2. y′′ – 2y′ – 8y = 0.
3.  4.
4. 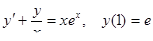 5.
5. 
|
Вариант 4
Найти общее решение дифференциального уравнения
1. yy′ + x = 0;
2. y′′ – 8y + 16 = 0
3. 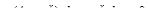 4.
4. 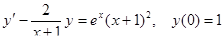 5.
5. 
|
Вариант 5
Найти общее решение дифференциального уравнения
1. 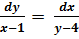 ;
2. ;
2. 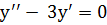 3.
3. 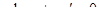 4.
4. 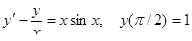 5.
5. 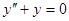
|
Вариант 6
Найти общее решение дифференциального уравнения
1. y′ = 5x;
2. y′′ – 3y′ + 2y = 0
3. 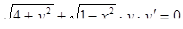 4.
4. 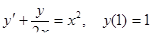 5.
5. 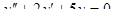
|
Вариант 7
Найти общее решение дифференциального уравнения
1. y′ = x2 + x;
2. y′’ + 4y = 0
3. 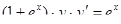 4.
4. 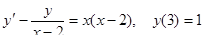 5.
5. 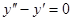
|
Вариант 8
Найти общее решение дифференциального уравнения
1. y′ = x3 + 1;
2. y′′ – 8y + 15y = 0
3. 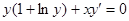 4.
4. 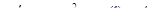 5.
5. 
|
Вариант 9
Найти общее решение дифференциального уравнения
1. y′ = 8x3;
2. y′′ – 6y′ + 5y = 0;
3. 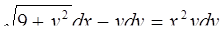 4.
4. 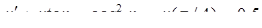 5.
5. 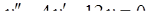
|
Вариант 10
Найти общее решение дифференциального уравнения
1. 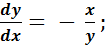 2. y′′ – 4y′ + 13y = 0.
3.
2. y′′ – 4y′ + 13y = 0.
3. 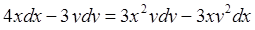 4.
4. 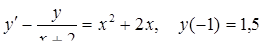 5.
5. 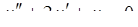
|
Дата: 2018-11-18, просмотров: 518.