у
+ +
0 a - bx
Известно, что определенный интеграл на отрезке представляет собой площадь криволинейной трапеции, ограниченной графиком функции f(x). Если график расположен ниже оси Ох, т.е. f(x) < 0, то площадь имеет знак “-“, если график расположен выше оси Ох, т.е. f(x) > 0, то площадь имеет знак “+”.
Для нахождения суммарной площади используется формула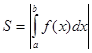 
.
Площадь фигуры, ограниченной некоторыми линиями может быть найдена с помощью определенных интегралов, если известны уравнения этих линий.
Пример. Найти площадь фигуры, ограниченной линиями y = x, y = x2, x = 2.
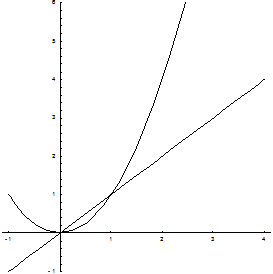
Искомая площадь (заштрихована на рисунке) может быть найдена по формуле:
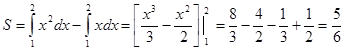(ед2)
Пример.
Вычислить площадь области, ограниченной кривыми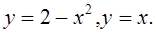 
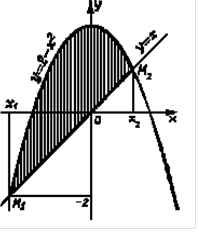
Р е ш е н и е.
Определим точки пересечения данных кривых. В точке пересечения ординаты равны, т. е.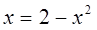 
, отсюда 
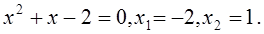Мы получили две точки пересечения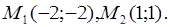 
Следовательно, искомая площадь
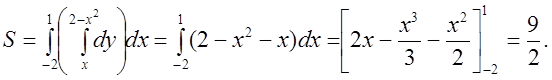(ед2)
ЗАДАНИЯ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ
Вариант 1:
Найти неопределенные интегралы и вычислить определенный интеграл:
а)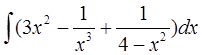 
б) 
в) 
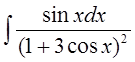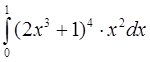
Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж.
Вариант 2:
Найти неопределенные интегралы и вычислить определенный интеграл:
а)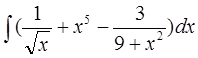 
б) 
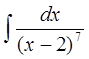в)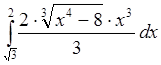 
Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж.
Вариант 3:
Найти неопределенные интегралы и вычислить определенный интеграл:
а)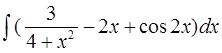 
б) 
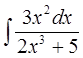в)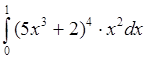 
Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж.
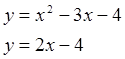
Вариант 4:
Найти неопределенные интегралы и вычислить определенный интеграл:
а)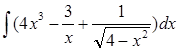 
б) 
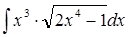в)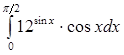 
Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж.
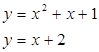
Вариант 5:
Найти неопределенные интегралы и вычислить определенный интеграл:
а)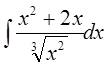 
б) 
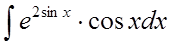в)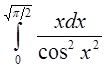 
Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж.
Вариант 6:
Найти неопределенные интегралы и вычислить определенный интеграл:
а)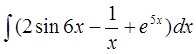 
б) 
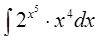в)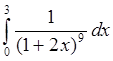 
Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж.
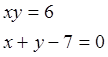
Вариант 7:
Найти неопределенные интегралы и вычислить определенный интеграл:
а)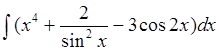 
б) 
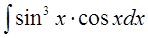в)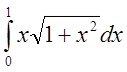 
Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж.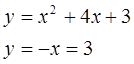 
Вариант 8:
Найти неопределенные интегралы и вычислить определенный интеграл:
а)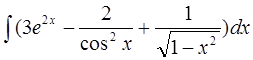 
б) 
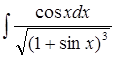в)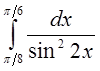 
Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж.
Вариант 9:
Найти неопределенные интегралы и вычислить определенный интеграл:
а)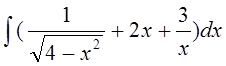 
б) 
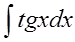в)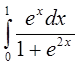 
Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж.
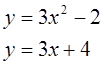
Вариант 10:
Найти неопределенные интегралы и вычислить определенный интеграл:
а)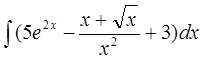 
б) 
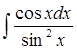в)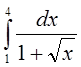 
Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж.
ТЕМА 5. ТЕОРИЯ ПРЕДЕЛОВ
| Предел функции в точке | знать: определение предела, свойства пределов уметь: вычислять пределы функции |
| Второй замечательный предел | знать: второй замечательный предел уметь: использовать второй замечательный предел при вычислении пределов |
| Способы задания числовых последовательностей | знать: способы задания числовых последовательностей уметь: вычислять члены последовательности |
| Раскрытие неопределенности вида «бесконечность на бесконечность» | знать: способы раскрытия неопределенностей вида «бесконечность на бесконечность» уметь: вычислять пределы, имеющие неопределенности вида «бесконечность на бесконечность» |
| Раскрытие неопределенности вида «ноль на ноль» | знать: способы раскрытия неопределенностей вида «ноль на ноль» уметь: вычислять пределы, имеющие неопределенности вида «ноль на ноль» |
| Первый замечательный предел | знать: первый замечательный предел уметь: использовать первый замечательный предел при вычислении пределов |
Дата: 2018-11-18, просмотров: 250.
