Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Определение: Дифференциальное уравнение с разделяющи-мися переменными имеет вид  

M₁(x)·N₁(y))dx + M₂(x)·N₂(y)dy=0.

Алгоритм решения:

1) Поделим все члены уравнения наN ₁ ( y ) ·M ₂ ( x ), получим:

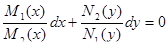, здесь переменные разделены.

2) Интегрируем обе части равенства:

,

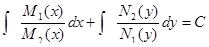после чего находим общее решение данного дифференциального уравнения в виде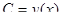

Пример: Найти общее решение дифференциального уравнения:             со s ² y·ctgxdx + sin²x tgydy=0.

Решение: 

Разделим на cos ² y · sin ² y

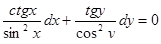, переменные разделены.

Проинтегрируем обе части полученного равенства.

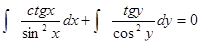
Интегралы находим методом подстановки.

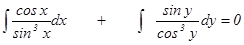
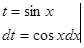
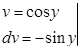
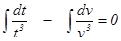
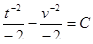или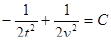

Произведя обратную подстановку, получим:

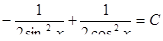или 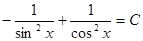                Отсюда,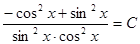 

Ответ: 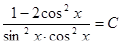- общее решение уравнения.

Однородные дифференциальные уравнения

Первого порядка

Определение: Однородной функцией переменных x и y называется функция, все члены которой имеют одинаковую степень.

Например, 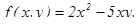 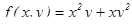- однородные функции второй и третьей степени соответственно.

 

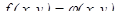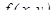Определение: Уравнение вида , где    и 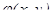 - однородные функции одной и той же степени, называетсяоднородным дифференциальным уравнением первого порядка.

Однородное уравнение приводится к уравнению с разделяющими переменными подстановкой, где 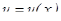– новая искомая функция.

Пример 1: Найти общее решение уравнения

.

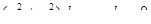Решение: Положим 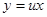. Дифференцируя равенство y = ux, получим 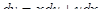. Подставляя выражения в уравнение, получим: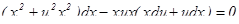  

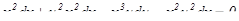
Разделим переменные в полученном уравнении.

;             

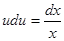
Интегрируем, 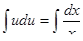. Отсюда, .

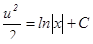Сделаем обратную замену: 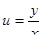  , получим .

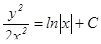Ответ: .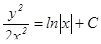

Линейные дифференциальные уравнения

Первого порядка

Определение: Уравнение вида 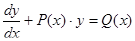 называется линейным дифференциальным уравнением первого порядка.

 

Уравнения такого вида сводятся к двум уравнениям с разделяющимися переменными с помощью подстановки 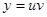, где 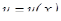,  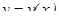- некоторые функции, зависящие от x.

 

Алгоритм решения:

1) Вводится подстановка 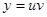, тогда .

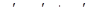2) Исходное уравнение принимает вид:         

.

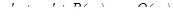3) Группируются слагаемые при u.

.

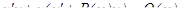4) Выражение в скобках приравнивается к нулю:

.

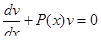Это уравнение с разделяющимися переменными, решая его, находим .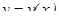

5) Полученное значение v подставляется в выражение:

.

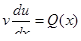Решив уравнение с разделяющимися переменными, получим функцию .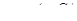

6) Общее решение уравнения запишется в виде:

.

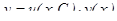Пример 1: Найти общее решение уравнения

.

 

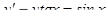Решение: Обозначим 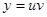, тогда .

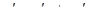Уравнение примет вид .

Вынесем во втором и третьем слагаемом общий множитель за скобки, получим      .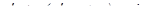

Выражение в скобках приравняем к нулюv ′ - vtgx = 0

Перепишем в виде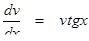

Умножая обе части уравнения на 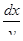, получим ,

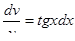интегрируем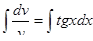                                                    

находим 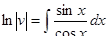, применим замену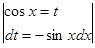

получим ,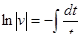

откуда 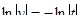или , .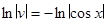

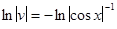Пропотенцируем обе части равенстваv =  .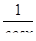

Найденную функцию 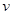 подставим в выражение  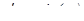и решим полученное уравнение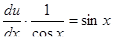

du = sinx ∙ cos ∙ xdxили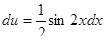

Интегрируем   ,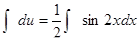

Получим          .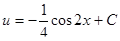

Зная функции u и v , можно записать ответ.

Ответ: Общее решение уравнения у = .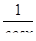

 

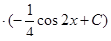Пример 2: Найти частное решение дифференциального уравнения 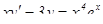, есл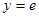и при .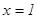

 

Решение: Пусть 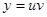, тогда .

Отсюда, .

Вынесем u за скобки: .

Приравняв скобку к 0 , получим: .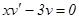

Отсюда, , .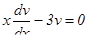

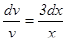Интегрируем ,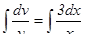

, , .

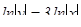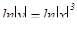Подставив   в выражение , получим уравнение относительно функции u и решим его.

, , , .

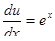Проинтегрируем 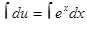. Функция .

Запишем общее решение уравнения : .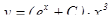

Частное решение найдем из условия 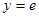при .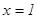

, ,     .

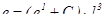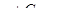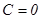Частное решение заданного уравнения имеет вид: .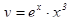

Ответ: 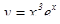 - частное решение уравнения.