Системой линейных уравнений с тремя неизвестными называется система вида:
Решить систему (1) – значит найти такие значения (x, y, z), при подстановке которых в систему уравнения становятся верными тождествами. Для решения таких систем существует много способов. Рассмотрим три основных: метод Гаусса, метод Крамера, метод обратной матрицы.
Рассмотрим систему уравнений:
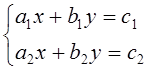
Данную систему можно решить традиционными методами – подстановки и сложения уравнений. Однако в ряде случаев оказывается легче применить определители (детерминанты)(метод Крамера):
Представим систему в виде квадратной матрицы: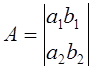 
число а1b2– а2b1 называют определителем системы и обозначаютdetA или D.
, 
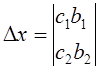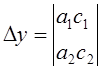
Определитель Dx получается изDзаменой элементов первого столбца свободными членами системы; аналогично Dy.
Возможны три случая
С л у ч а й 1: определитель системы не равен нулю: D ¹ 0. Тогда система имеет единственное решение: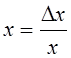 
x, 
.
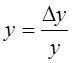С л у ч а й 2: определитель системы равен нулю: D = 0 (т. е. коэффициенты при неизвестных пропорциональны). Пусть при этом один из определителей Dx, Dy не равен нулю (т. е. свободные члены не пропорциональны коэффициентам при неизвестных). В этом случае системы не имеет решений.
С л у ч а й 3: D = 0, Dx = 0, Dy = 0 (т. е. коэффициенты и свободные члены пропорциональны). Тогда одно из уравнений есть следствие другого: система сводится к одному уравнению с двумя неизвестными и имеет бесчисленное множество решений.
Аналогично поступают и в случае системы трех уравнений с тремя неизвестными:
Пусть требуется решить систему уравнений:
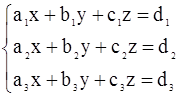
1. Вычисляем определитель системы: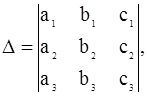 
если Δ ≠ 0, тогда система имеет единственное решение, в противном случае решений либо бесконечно много, либо не существует.
2. Вычисляем вспомогательные определители: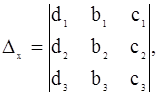 
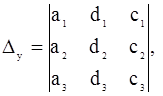
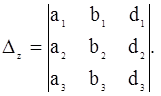
3. Находим x, y, z:
.
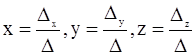ЗАДАНИЯ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ
Вариант 1
1. Решить систему линейных алгебраических уравнений методом Крамера
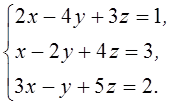
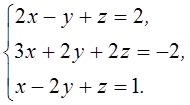
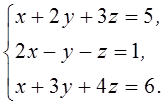
2. Даны матрицы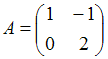 
и 
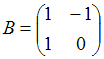. Найти матрицу С = 
.
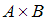3. Даны матрицы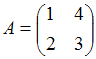 
и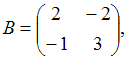 
Найти матрицуС = А + 2В
Вариант 2
1. Решить систему линейных алгебраических уравнений методом Крамера
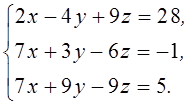
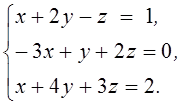
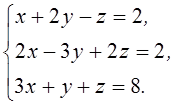
2. Даны матрицы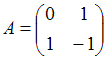 
и 
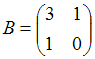. Найти матрицу С = .
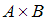3. Даны матрицы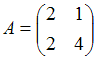 
и 
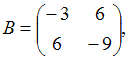найти матрицу
С = А- 
В
Вариант 3
1. Решить систему линейных алгебраических уравнений методом Крамера
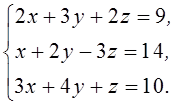
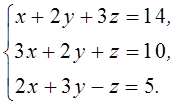
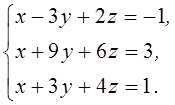
2. Даны матрицы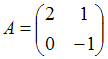 
и 
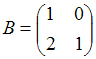.Найти матрицу С =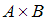
3. Даны матрицы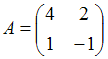 
и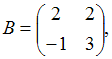 
найти матрицу С = А – 2В.
Вариант 4
1. Решить систему линейных алгебраических уравнений методом Крамера
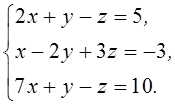
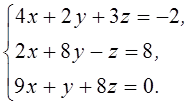
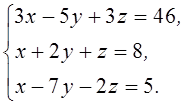
2. Даны матрицы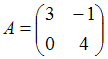 
и 
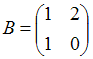. Найти матрицу С =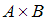
3. Даны матрицы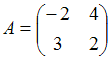 
и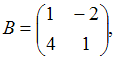 
найти матрицу С = 2А –В.
Вариант 5
1. Решить систему линейных алгебраических уравнений методом Крамера
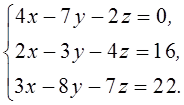
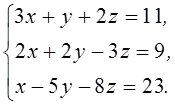
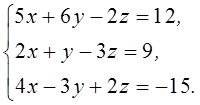
2. Даны матрицы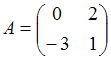 
и 
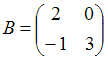. Найти матрицу С =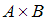
3. Даны матрицы 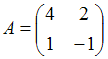и 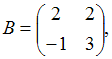найти матрицу С = А – 2В.
Вариант 6
1. Решить систему линейных алгебраических уравнений методом Крамера
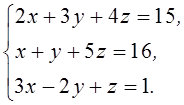
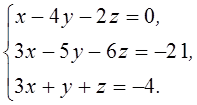
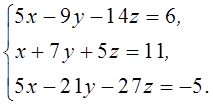
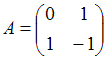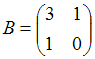2. Даны матрицы и . Найти матрицу С =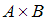
3. Даны матрицы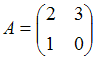 
и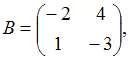 
найти матрицу С = 3А – В.
Вариант 7
1. Решить систему линейных алгебраических уравнений методом Крамера
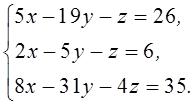
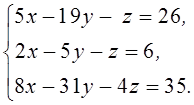
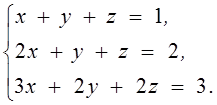
2. Даны матрицы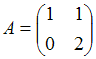 
и 
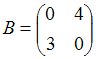. Найти матрицу С =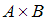
3. Даны матрицы 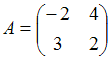и 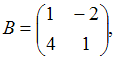найти матрицу С = А – 2В.
Вариант 8
1. Решить систему линейных алгебраических уравнений методом Крамера
2.
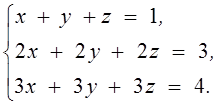
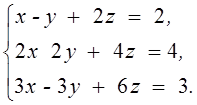
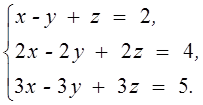
3. Даны матрицы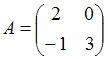 
и 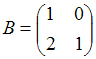. Найти матрицу С =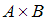
4. Даны матрицы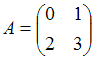 
и 
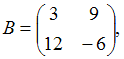найти матрицу С = А- 
В
Вариант 9
1. Решить систему линейных алгебраических уравнений методом Крамера
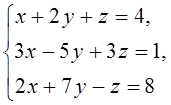
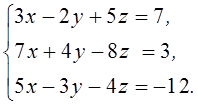
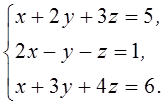
2. Даны матрицы 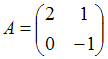и 
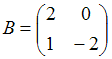Найти матрицу С =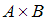
3. Даны матрицы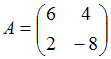 
и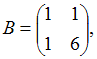 
найти матрицу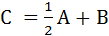 
Вариант 10
1. Решить систему линейных алгебраических уравнений методом Крамера
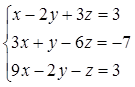
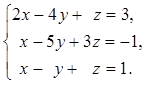
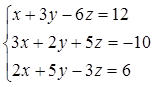
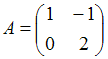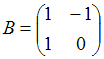2. Даны матрицы и . Найти матрицу С =
3. Даны матрицы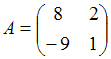 
и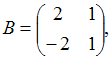 
найти матрицу С = 3А-В.
ПРИМЕРЫ РЕШЕНИЙ
1. Даны матрицы А =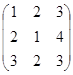 
; B =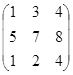 
, найти 2А + В.
Решение:
2А =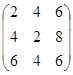 
, 2А + В = 
.
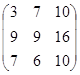2. Найти произведение матриц А=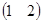 
, В = 
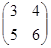
Решение:
АВ = × =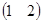 
= 
.
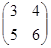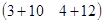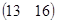3. Даны матрицы А =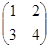 
, В =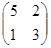 
. Найти матрицу С = A×B.
Решение:
С = AB =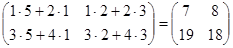 
.
4. Дана матрица А =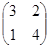 
, найти А3.
А2 = АА = =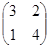 
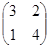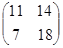; A3 = =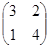 
.
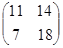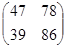5. Вычислить определитель матрицы А =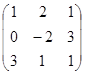 
Решение:
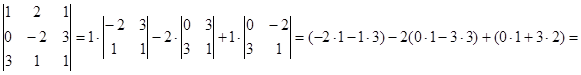
= -5 + 18 + 6 = 19.
Второй способ:
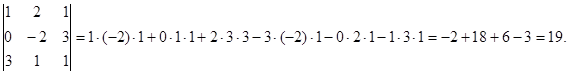
6. Найти решение системы уравнений: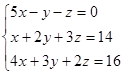 
Решение:
D =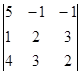 
= 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;
D1 =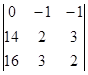 
= (28 – 48) – (42 – 32) = -20 – 10 = -30.
x1 = D1/D = 1;
D2 =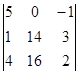 
= 5(28 – 48) – (16 – 56) = -100 + 40 = -60.
x2 = D2/D = 2;
D3 =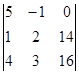 
= 5( 32 – 42) + (16 – 56) = -50 – 40 = -90.
x3 = D3/D = 3.
Ответ: (1; 2; 3)
Дата: 2018-11-18, просмотров: 264.
