Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

графика функции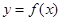

1. Найти вторую производную .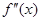

2. Найти критические точки II рода функции 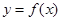, т.е. точки, в которой 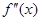обращается в нуль или терпит разрыв.

3. Исследовать знак второй производной 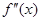впромежутка, на которые найденные критические точки делят область определения функции 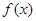. Если при этом критическая точка  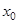разделяет промежутки выпуклости противоположных направлений, то  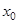является абсциссой точки перегиба графика функции.

4. Вычислить значения функции в точках перегиба.

 

Пример 1: Найти промежутки выпуклости и точки перегиба следующей кривой:        .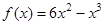

Решение: Находим , .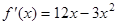

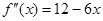Найдем критические точки по второй производной, решив уравнение         .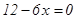

.

 

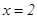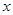
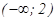
		2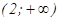
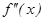
	+	0	-
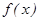
		точка перегиба 16

 

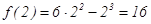
Ответ: Функция выпукла вверх при ;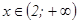

функция выпукла вниз при ;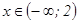

         точка перегиба .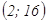

 

Общая схема для построения графиков функций

 

1. Найти область определения функции .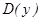

2. Найти точки пересечения графика функций с осями координат.

3. Исследовать функцию на четность или нечетность.

4. Исследовать функцию на периодичность.

5. Найти промежутки монотонности и точки экстремума функции.

6. Найти промежутки выпуклости и точки перегиба функции.

7. Найти асимптоты функции.

8. По результатам исследования построить график .

Пример: Исследовать функцию и построить ее график:

.

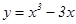Решение:

1) Функция определена на всей числовой оси, т. е. ее область определения .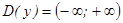

2) Найдем точки пересечения с осями координат:

с осью ОХ : решим уравнение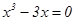

.

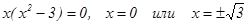с осью ОY: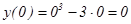

3) Выясним, не является ли функция четной или нечет

ной:

.

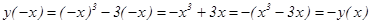Отсюда следует, что функция является нечетной.

4) Функция непериодична.

5) Найдем промежутки монотонности и точки экстремума функции: .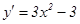

Критические точки: .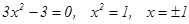

 

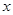
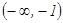
		-1		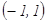1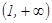
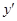
	+	0	-	0	+
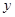
		т. max 2		т. min -2

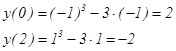
6) Найдем промежутки выпуклости и точки перегиба функции: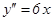               

Критические точки: .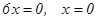

 

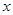
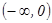
		0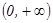
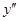
	-	0	+
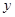
		точка перегиба 0

            

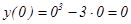
7) Функция непрерывна, асимптот у нее нет.

8) По результатам исследования построим график функции:

y

 

 

                                          2

 

 

1           x

                                         -2

 

ЗАДАНИЯ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ

Вариант 1

1. Найти производные функций

2. Исследовать функцию и построить ее график:

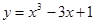
3. Вычислить приближенно значение функции у = 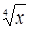в точке x = 17

 

 

Вариант 2

1. Найти производные функций

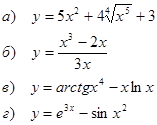
2. Исследовать функциюи построить ее график:

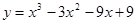
3.  Вычислить приближенно значение функции у =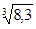

Вариант 3

1. Найти производные функций

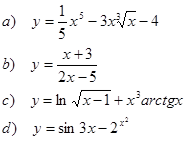
2. Исследовать функциюи построить ее график:

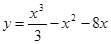
3.  Вычислить приближенно значение функции у =1,015²

Вариант 4

1. Найти производные функций

2. Исследовать функциюи построить ее график:

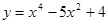
3.  Вычислить приближенно значение функции у = 1,004⁴

Вариант 5

1. Найти производные функций

 

                         
2. Исследовать функциюи построить ее график:

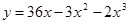
3.  Вычислить приближенно значение функции у =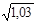

 

Вариант 6

1. Найти производные функций

 

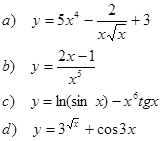
2. Исследовать функциюи построить ее график:

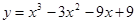
3.  Вычислить приближенно значение функции у =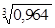

 

Вариант 7

1. Найти производные функций

 

 

2. Исследовать функцию и построить ее график:

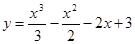
3. Вычислить приближенно значение функции у = 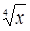в точке x = 80

Вариант 8

1. Найти производные функций

 

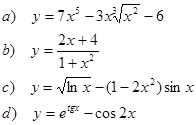
2. Исследовать функциюи построить ее график:

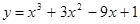
3.  Вычислить приближенно значение функции у =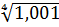

 

Вариант 9

1. Найти производные функций

 

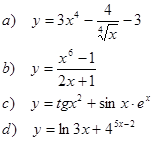
2. Исследовать функциюи построить ее график:

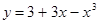
^3.  Вычислить приближенно значение функции у =1,002³

 

Вариант10

1. Найти производные функций

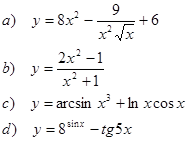
2. Исследовать функциюи построить ее график:

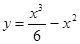
^3.  Вычислить приближенно значение функции у =0,97⁴