Вариант 1
1. Решить квадратное уравнение:
х2 + 2х + 5 = 0.
2. Найти действительные числа x и y из условия равенства двух комплексных чисел
5х – 2у + (х + у)i = 4 + 5i .
3. Выполнить действия:
a. 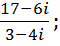
b. (1 - i)3;
c. i40 – i21.
4. Выполнить действия и записать результат в тригонометрической форме:
a. 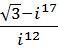
b. 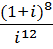
5. Изобразить решения, полученные в пункте 4, на комплексной плоскости
Вариант 2
1. Решить квадратное уравнение:
х2 + 2х + 4 = 0.
2. Найти действительные числа x и y из условия равенства двух комплексных чисел
5х i – 2+ 4у = 9i + 2x + 3yi .
3. Выполнить действия:
a. 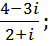
b. (1 + i)3;
c. i3 – i100.
4. Выполнить действия и записать результат в тригонометрической форме:
a. 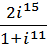
b. 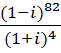
5. Изобразить решения, полученные в пункте 4, на комплексной плоскости
Вариант 3
1. Решить квадратное уравнение:
х2-6х + 18 = 0.
2. Найти действительные числа x и y из условия равенства двух комплексных чисел
9 + 2х i+4у i= 10i + 5x – 6y .
3. Выполнить действия:
a. 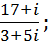
b. (1 - i)4;
c. i13 – i33.
4. Выполнить действия и записать результат в тригонометрической форме:
a. 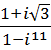
b. 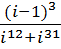
5. Изобразить решения, полученные в пункте 4, на комплексной плоскости
Вариант 4
1. Решить квадратное уравнение:
х2-4х + 5 = 0.
2. Найти действительные числа x и y из условия равенства двух комплексных чисел
2х i+3у i+ 17 = 3x + 2y + 18i .
3. Выполнить действия:
a. 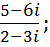
b. (1 - i)4;
c. i17 – i38.
4. Выполнить действия и записать результат в тригонометрической форме:
a. 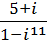
b. 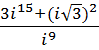
5. Изобразить решения, полученные в пункте 4, на комплексной плоскости
Вариант 5
1. Решить квадратное уравнение:
х2 + 6х + 10 = 0.
2. Найти действительные числа x и y из условия равенства двух комплексных чисел
4х+5у – 9 + 7 (3х-у)i = 10x + 14yi .
3. Выполнить действия:
a. 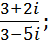
b. (3 - 4i)3;
c. i15 – i37.
4. Выполнить действия и записать результат в тригонометрической форме:
a. 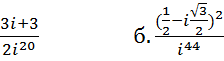
5. Изобразить решения, полученные в пункте 4, на комплексной плоскости
Вариант 6
1. Решить квадратное уравнение:
х2-10х + 41 = 0.
2. Найти действительные числа x и y из условия равенства двух комплексных чисел
3 + 4х i+5у i=12i + 5x – 2y .
3. Выполнить действия:
a. 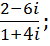
b. (2 + 5i)3;
c. i23 – i111.
4. Выполнить действия и записать результат в тригонометрической форме:
a. 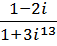
b. 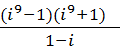
5. Изобразить решения, полученные в пункте 4, на комплексной плоскости
Вариант 7
1. Решить квадратное уравнение:
2х2- 2х + 5 = 0.
2. Найти действительные числа x и y из условия равенства двух комплексных чисел
х(2 + i) –у (1-i ) = 1 + 3i .
3. Выполнить действия:
a. 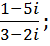
b. (1 + 7i)3;
c. i45 – i11.
4. Выполнить действия и записать результат в тригонометрической форме:
a. 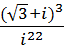
b. 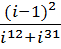
5. Изобразить решения, полученные в пункте 4, на комплексной плоскости
Вариант 8
1. Решить квадратное уравнение:
25х2- 20х + 13 = 0.
2. Найти действительные числа x и y из условия равенства двух комплексных чисел
х(1 + i) + y(2 – 3i) = 3i + 1.
3. Выполнить действия:
a. 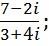
b. (1 - 5i)3;
c. i58 – i51.
4. Выполнить действия и записать результат в тригонометрической форме:
a. 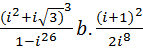
5. Изобразить решения, полученные в пункте 4, на комплексной плоскости
Вариант 9
1. Решить квадратное уравнение:
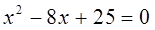 .
.
2. Найти действительные числа x и y из условия равенства двух комплексных чисел
9 + 2ix+4iy = 10i+5x-6y .
3. Выполнить действия:
a. 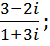
b. (3 - 2i)3;
c. i15 – i57.
4. Выполнить действия и записать результат в тригонометрической форме:
a. 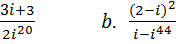
5. Изобразить решения, полученные в пункте 4, на комплексной плоскости
Вариант 10
1. Решить квадратное уравнение:
х2-6х + 18 = 0.
2. Найти действительные числа x и y из условия равенства двух комплексных чисел
2х i+3у i+ 17= 3x + 2y + 18 .
3. Выполнить действия:
a. 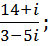
b. (1 - 2i)4;
c. i23 – i35.
4. Выполнить действия и записать результат в тригонометрической форме:
a. 
5. Изобразить решения, полученные в пункте 4, на комплексной плоскости.
ПРИМЕРЫ РЕШЕНИЙ
1. Решите во множестве комплексных чисел уравнение 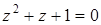 .
.
Решение:
Так как 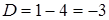 , тогда корни находятся по формуле
, тогда корни находятся по формуле 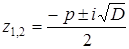
( 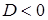 ).
).
Отсюда, 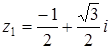 ,
, 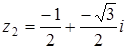 .
.
Ответ: 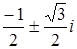 .
.
.
Решите уравнение 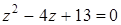
Решение:
По формуле 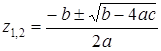 , находим:
, находим:
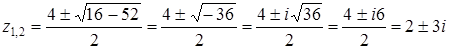 .
.
2. При каких действительных значениях x и y комплексные числа 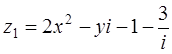 и
и 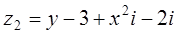 будут равными?
будут равными?
Решение:
Комплексные числа 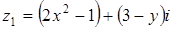 и
и 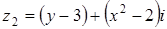 будут равными, если выполняются условия:
будут равными, если выполняются условия:
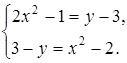
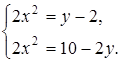
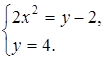
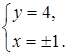
Ответ: 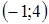 ;
; 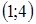 .
.
3. Вычислите 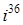 ;
; 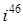 ;
; 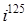 ;
; 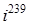 .
.
Решение:
С помощью формулы: 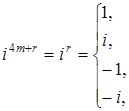
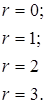
легко получаем:
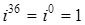 ;
;
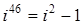 ;
;
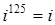 ;
;
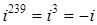 .
.
Ответ: 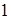 ;
; 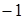 ;
; 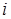 ;
; 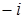 .
.
4. Выполнить все действия над комплексными числами 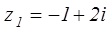 и
и 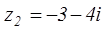 .
.
Решение
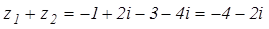
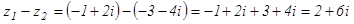
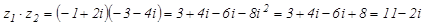
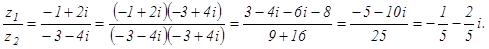
5. Выполните указанные действия: 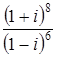 .
.
Решение
Вычислим значение дроби 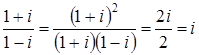 .
.
Следовательно, 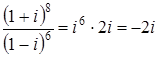
Ответ: 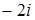 .
.
6. Изобразите на комплексной плоскости следующие комплексные числа:
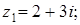
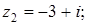
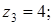
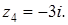
Решение
Данным комплексным числам соответствуют точки комплексной плоскости.
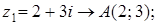
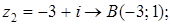
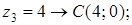
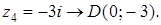
Покажем их.

7. Запишите комплексные числа в тригонометрической форме:
а) 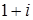 ; б)
; б) 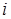 ; в)
; в) 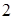 ; г)
; г) 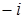 ; д)
; д) 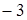 ; е)
; е) 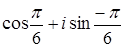 ; ж)
; ж) 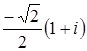 .
.
Решение
Так как тригонометрическая форма комплексного числа имеет вид 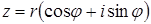 , тогда:
, тогда:
а) В комплексном числе 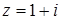 :
: 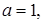
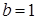 .
.
Тогда 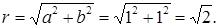
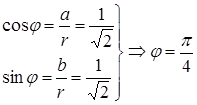 ,
,
Поэтому 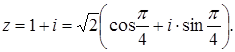
б) 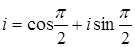 , где
, где 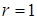 ,
, 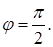
в) 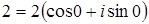 , где
, где 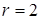 ,
, 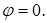
г) 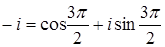 , где
, где 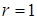 ,
, 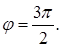
д) 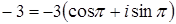 , где
, где 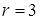 ,
, 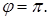
е) 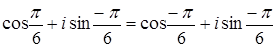 .
.
ж) 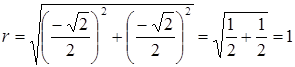 , а
, а 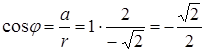 , то
, то 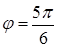 .
.
Поэтому 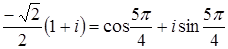
Ответ: 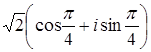 ;
; 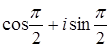 4;
4; 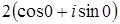 ;
; 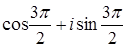 ;
; 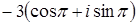 ;
; 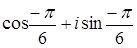 ;
; 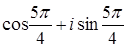 .
.
Действия с матрицами
1) Суммой двух матриц одинаковой размерности, называется матрица той же размерности, каждый элемент которой равен сумме соответствующих элементов слагаемых.
2) По определению, чтобы умножить матрицу на число, нужно умножить на это число все элементы матрицы.
3) Произведение матриц определяется следующим образом. Пусть заданы две матрицы A и B, причем число столбцов первой из них равно числу строк второй. Если
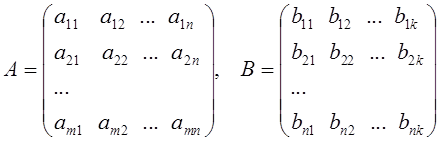 ,
,
то произведением матрицA и B, называется матрица
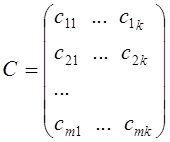 ,
,
элементы которой вычисляются по формуле
cij= a i1 b 1j + a i2 b 2j+ ... +a in bnj , i = 1, ..., m, j = 1, ..., k.
Произведение матриц A и B обозначается AB, т. е. C = AB.
Пусть даны матрицы 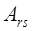 и
и 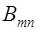 .
.
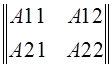 ·
· 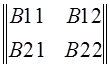 =
= 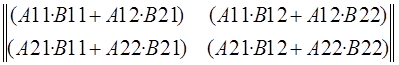
Получаем матрицуС, каждый элемент которой равен сумме произведений элементов i-ой строки матрицы А на соотв. элемент j-го столбца матрицы В.
ПроизведениеА · Вопределено, если s= m (число столбцов А равно числу строк В). Если 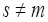 , то произведениеА · В найти нельзя.
, то произведениеА · В найти нельзя.
Определители
Определители (детерминанты) рассматриваются только для квадратных матриц.
Определитель n -го порядка это число, записываемое в виде таблицы
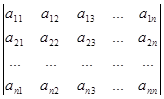
и может быть вычислено по элементам этой таблицы в соответствии с указанными ниже правилами.
Минором Mij элемента aij называется определитель ( n -1)-го порядка, полученный из определителя n-гопорядка вычеркиванием i-й строки и j-го столбца.
Алгебраическое дополнение Aij элемента aij определяется равенством:
Aij =(-1) i + j Mij.
Определитель D n ( det ) находится по правилу:
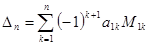 ,
,
а миноры M 1 k – являются определителем ( n -1)-го порядка, полученным из D n вычеркиванием 1-й строки и k-го столбца. Эта формула называется разложением по строке. Можно раскладывать по столбцу:
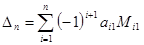 .
.
Определители первого, второго и третьего порядков
Определитель первого порядка 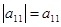 .
.
Определитель второго порядка:
D2= 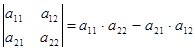 .
.
Определитель третьего порядка, вычисленный разложением по первой строке:
D3= 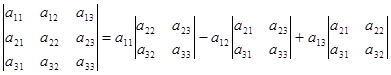 .
.
Правило вычисления определителя 3-го порядка равносильно правилу треугольников (правилу Саррюса):
D3=a11a22a33+ a12a23a31+ a21a32a13-(a13a22a31+ a12a21a33+ a23a32a11).
Чтобы запомнить, какие произведения в правой части равенства берутся со знаком «+», а какие со знаком «–», полезно использовать следующее правило треугольников (или правило Саррюса):
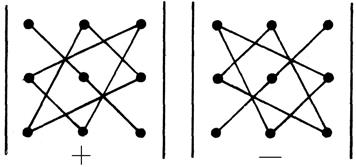
Это правило позволяет легко записать формулу вычисления определителя 3-го порядка и найти его.
ЗАДАНИЯ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ
Вариант 1
1. Решить систему линейных алгебраических уравнений методом Крамера
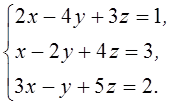
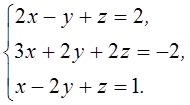
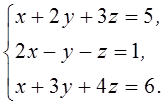
2. Даны матрицы 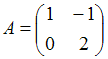 и
и 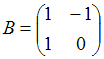 . Найти матрицу С =
. Найти матрицу С = 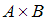 .
.
3. Даны матрицы 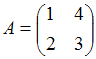 и
и 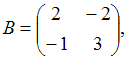 Найти матрицуС = А + 2В
Найти матрицуС = А + 2В
Вариант 2
1. Решить систему линейных алгебраических уравнений методом Крамера
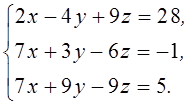
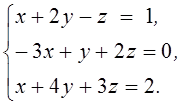
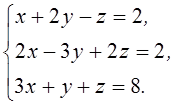
2. Даны матрицы 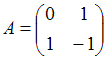 и
и 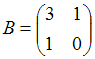 . Найти матрицу С =
. Найти матрицу С = 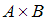 .
.
3. Даны матрицы 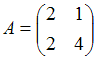 и
и 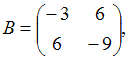 найти матрицу
найти матрицу
С = А-  В
В
Вариант 3
1. Решить систему линейных алгебраических уравнений методом Крамера
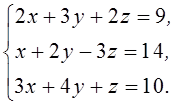
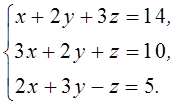
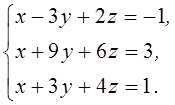
2. Даны матрицы 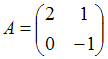 и
и 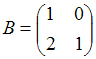 .Найти матрицу С =
.Найти матрицу С = 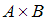
3. Даны матрицы 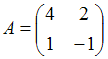 и
и 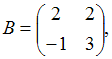 найти матрицу С = А – 2В.
найти матрицу С = А – 2В.
Вариант 4
1. Решить систему линейных алгебраических уравнений методом Крамера
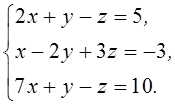
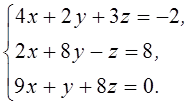
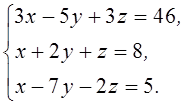
2. Даны матрицы 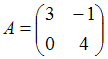 и
и 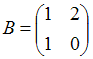 . Найти матрицу С =
. Найти матрицу С = 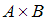
3. Даны матрицы 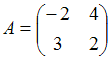 и
и 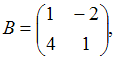 найти матрицу С = 2А –В.
найти матрицу С = 2А –В.
Вариант 5
1. Решить систему линейных алгебраических уравнений методом Крамера
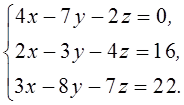
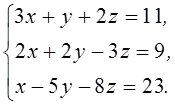
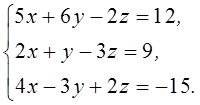
2. Даны матрицы 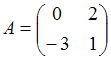 и
и 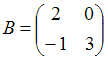 . Найти матрицу С =
. Найти матрицу С = 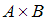
3. Даны матрицы 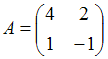 и
и 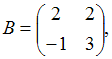 найти матрицу С = А – 2В.
найти матрицу С = А – 2В.
Вариант 6
1. Решить систему линейных алгебраических уравнений методом Крамера
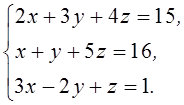
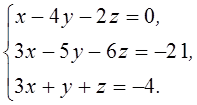
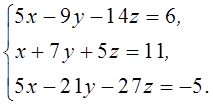
2. Даны матрицы 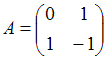 и
и 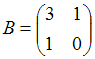 . Найти матрицу С =
. Найти матрицу С = 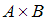
3. Даны матрицы 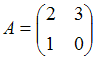 и
и 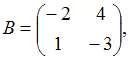 найти матрицу С = 3А – В.
найти матрицу С = 3А – В.
Вариант 7
1. Решить систему линейных алгебраических уравнений методом Крамера
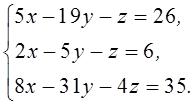
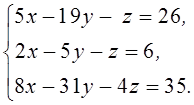
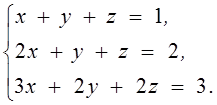
2. Даны матрицы 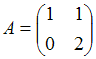 и
и 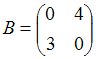 . Найти матрицу С =
. Найти матрицу С = 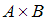
3. Даны матрицы 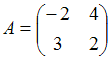 и
и 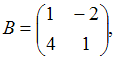 найти матрицу С = А – 2В.
найти матрицу С = А – 2В.
Вариант 8
1. Решить систему линейных алгебраических уравнений методом Крамера
2.
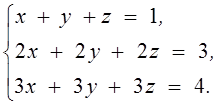
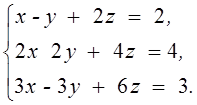
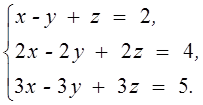
3. Даны матрицы 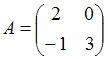 и
и 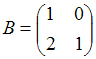 . Найти матрицу С =
. Найти матрицу С = 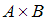
4. Даны матрицы 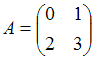 и
и 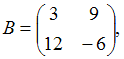 найти матрицу С = А-
найти матрицу С = А-  В
В
Вариант 9
1. Решить систему линейных алгебраических уравнений методом Крамера
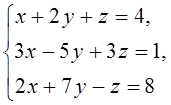
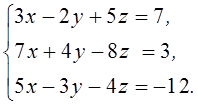
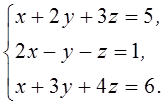
2. Даны матрицы 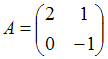 и
и 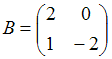 Найти матрицу С =
Найти матрицу С = 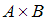
3. Даны матрицы 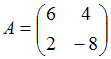 и
и 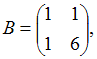 найти матрицу
найти матрицу 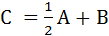
Вариант 10
1. Решить систему линейных алгебраических уравнений методом Крамера
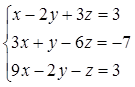
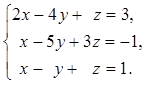
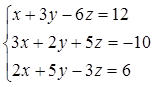
2. Даны матрицы 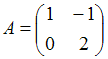 и
и 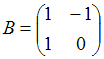 . Найти матрицу С =
. Найти матрицу С = 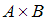
3. Даны матрицы 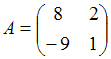 и
и 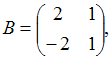 найти матрицу С = 3А-В.
найти матрицу С = 3А-В.
ПРИМЕРЫ РЕШЕНИЙ
1. Даны матрицы А = 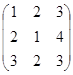 ; B =
; B = 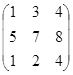 , найти 2А + В.
, найти 2А + В.
Решение:
2А = 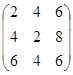 , 2А + В =
, 2А + В = 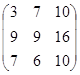 .
.
2. Найти произведение матриц А= 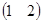 , В =
, В = 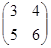
Решение:
АВ = 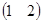 ×
× 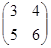 =
= 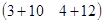 =
= 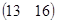 .
.
3. Даны матрицы А = 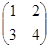 , В =
, В = 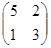 . Найти матрицу С = A×B.
. Найти матрицу С = A×B.
Решение:
С = AB = 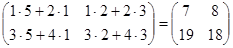 .
.
4. Дана матрица А = 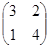 , найти А3.
, найти А3.
А2 = АА = 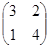
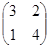 =
= 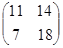 ; A3 =
; A3 = 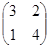
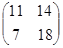 =
= 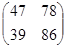 .
.
5. Вычислить определитель матрицы А = 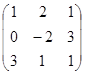
Решение:
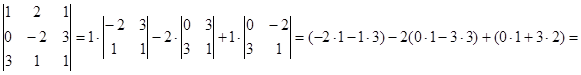
= -5 + 18 + 6 = 19.
Второй способ:
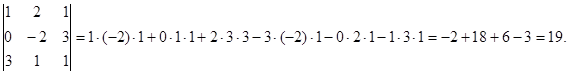
6. Найти решение системы уравнений: 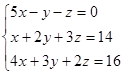
Решение:
D = 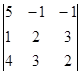 = 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;
= 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;
D1 = 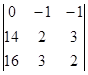 = (28 – 48) – (42 – 32) = -20 – 10 = -30.
= (28 – 48) – (42 – 32) = -20 – 10 = -30.
x1 = D1/D = 1;
D2 = 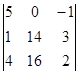 = 5(28 – 48) – (16 – 56) = -100 + 40 = -60.
= 5(28 – 48) – (16 – 56) = -100 + 40 = -60.
x2 = D2/D = 2;
D3 = 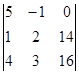 = 5( 32 – 42) + (16 – 56) = -50 – 40 = -90.
= 5( 32 – 42) + (16 – 56) = -50 – 40 = -90.
x3 = D3/D = 3.
Ответ: (1; 2; 3)
Понятие производной
Определение: Производной функции 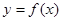 по аргументу x называется предел отношения ее приращения
по аргументу x называется предел отношения ее приращения 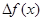 к приращению
к приращению 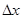 аргумента x, когда приращение аргумента стремится к нулю:
аргумента x, когда приращение аргумента стремится к нулю:
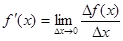 .
.
Если этот предел конечный, то функция y=f(x) называется дифференцируемой в точке x. Если же этотпредел есть ∞, то говорят, что функция y=f(x) имеет в точке x бесконечную производную.
Механический смысл производной: скорость есть первая производная пути по времени, т.е. 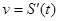 .
.
Геометрический смысл производной: тангенс угла наклона касательной к графику функции 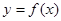 равен первой производной этой функции , вычисленной в точке касания, т.е.
равен первой производной этой функции , вычисленной в точке касания, т.е. 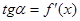
Уравнение касательнойк графику функции 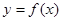 в точке
в точке 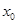 :
:
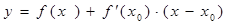
Уравнение нормали к графику функции 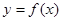 в точке
в точке 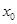 :
:
Таблица производных
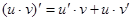
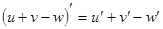
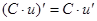
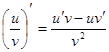
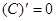
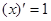
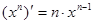
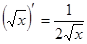
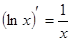

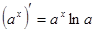
| 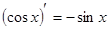
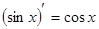
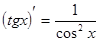
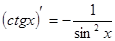
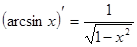
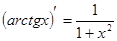
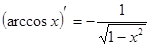
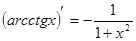
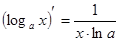
|
Процесс нахождения производных называется дифференцированием функции.
Рассмотрим примеры.
Найти производные функций:
Пример 1: 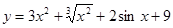
Решение: 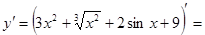
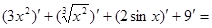
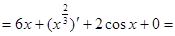
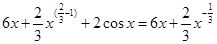 +
+
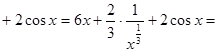
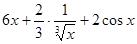
Пример2: 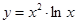
Решение: 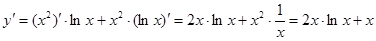
Пример 3: 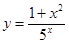
Решение: 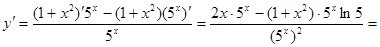
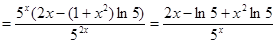
Дифференциал функции
Определение: Дифференциалом функции y = y ( x ) называется произведение ее производной на дифференциал независимой переменной:
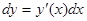 .
.
Для большей наглядности рассмотрим пример.
Пример 1: Найти дифференциал функции 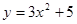
Решение: 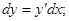
Так как 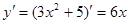 , то
, то 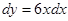 .
.
Для дифференцируемой в точке х0 функции f(x), у которой f¢(x0) ¹ 0, при достаточно малых ∆х справедливо приближенное равенство
∆f(x0) ~ df(x0) = f¢(x0)∆x
Т.к. ∆х = х – х0, ∆f(x0) = f(x0 + ∆x) – f(x0) = f(x) – f(x0),
то f(x) ~ f(x0) + f¢(x0) (x–x0)
Например, вычислим 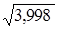 .
.
Рассмотрим функцию f(x) = 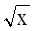 , х Î (0; +¥).
, х Î (0; +¥).
Для этой функции 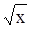 ~
~ 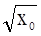 +
+ 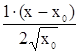
Подставляем х = 3,998 и х0= 4
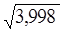 ~
~ 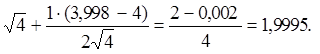
Производные высших порядков
Определение: Производная второго порядка (вторая производная) от функции y=f(x) есть производная от ее первой производной: 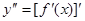 .
.
Определение:Производная n-ого порядка(n-я производная) от функции y = f ( x ) есть производная от ее (n -1)-й производной: 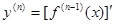 .
.
Рассмотрим примеры.
Пример 1: Найти производную второго порядка 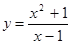 .
.
Решение: 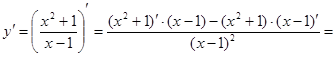
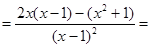
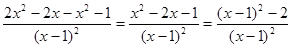
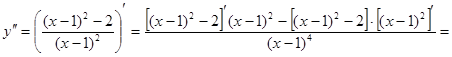
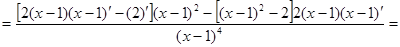
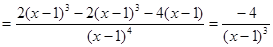
Пример2: Найти производную второго порядка функции 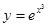 .
.
Решение: 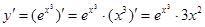
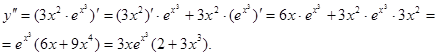
Исследование функции
С помощью производной
Определение: Точка х0 называется точкой локального максимума, если для любого х из окрестности точки х0 выполняется неравенство:
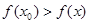 .
.
Определение: Точка х0 называется точкой локального минимума, если для любого х из окрестности точки х0 выполняется неравенство:
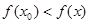 .
.
Точки минимума и максимума функции называются точками экстремума данной функции, а значения функции в этих точках – экстремумами функции.
Точками экстремума могут служить только критические точки I рода, т.е. точки, принадлежащие области определения функции, в которых производная 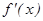 обращается в нуль или терпит разрыв.
обращается в нуль или терпит разрыв.
Правило нахождения экстремумов функции 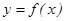
Точки перегиба
Определение: Кривая 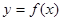 называется выпуклой вниз в промежутке
называется выпуклой вниз в промежутке 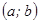 , если она лежит выше касательной в любой точке этого промежутка.
, если она лежит выше касательной в любой точке этого промежутка.
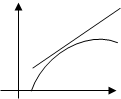 Определение: Кривая
Определение: Кривая 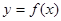 называется выпуклой вверх в промежутке
называется выпуклой вверх в промежутке 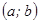 , если она лежит ниже касательной в любой точке этого промежутка.
, если она лежит ниже касательной в любой точке этого промежутка.
 yy
yy
xx
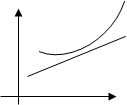
Определение: Промежутки, в которых график функции обращен выпуклостью вверх или вниз, называются промежутками выпуклости графика функции.
Выпуклость вниз или вверх кривой, являющейся графиком функции 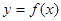 , характеризуется знаком ее второй производной: если в некотором промежутке
, характеризуется знаком ее второй производной: если в некотором промежутке 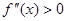 , то кривая выпукла вниз на этом промежутке; если же
, то кривая выпукла вниз на этом промежутке; если же 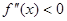 , то кривая выпукла вверх на этом промежутке.
, то кривая выпукла вверх на этом промежутке.
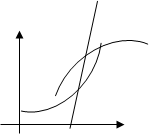
Определение: Точка графика функции 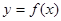 , разделяющая промежутки выпуклости противоположных направлений этого графика, называется точкой перегиба.
, разделяющая промежутки выпуклости противоположных направлений этого графика, называется точкой перегиба.
 |
y
x
Точками перегиба могут служить только критические точки II рода, т.е. точки, принадлежащие области определения функции 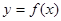 , в которых вторая производная
, в которых вторая производная 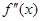 об-
об-
ращается в нуль или терпит разрыв.
ЗАДАНИЯ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ
Вариант 1
1. Найти производные функций

2. Исследовать функцию и построить ее график:
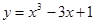
3. Вычислить приближенно значение функции у = 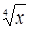 в точке x = 17
в точке x = 17
Вариант 2
1. Найти производные функций
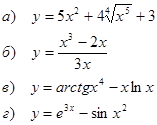
2. Исследовать функциюи построить ее график:
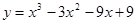
3. Вычислить приближенно значение функции у = 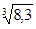
Вариант 3
1. Найти производные функций
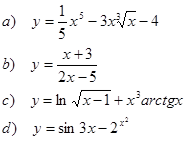
2. Исследовать функциюи построить ее график:
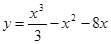
3. Вычислить приближенно значение функции у =1,0152
Вариант 4
1. Найти производные функций

2. Исследовать функциюи построить ее график:
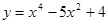
3. Вычислить приближенно значение функции у = 1,0044
Вариант 5
1. Найти производные функций

2. Исследовать функциюи построить ее график:
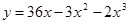
3. Вычислить приближенно значение функции у = 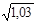
Вариант 6
1. Найти производные функций
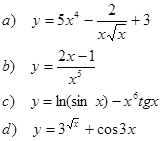
2. Исследовать функциюи построить ее график:
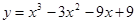
3. Вычислить приближенно значение функции у = 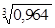
Вариант 7
1. Найти производные функций

2. Исследовать функцию и построить ее график:
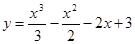
3. Вычислить приближенно значение функции у = 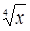 в точке x = 80
в точке x = 80
Вариант 8
1. Найти производные функций
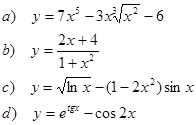
2. Исследовать функциюи построить ее график:
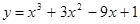
3. Вычислить приближенно значение функции у = 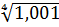
Вариант 9
1. Найти производные функций
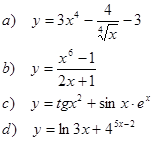
2. Исследовать функциюи построить ее график:
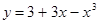
3. Вычислить приближенно значение функции у =1,0023
Вариант10
1. Найти производные функций
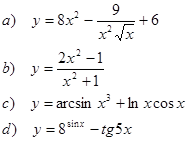
2. Исследовать функциюи построить ее график:
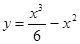
3. Вычислить приближенно значение функции у =0,974
Таблица интегралов
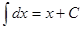
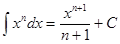
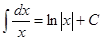
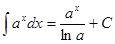
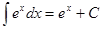
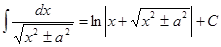
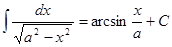
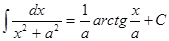 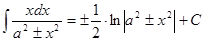
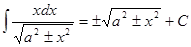
| 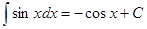
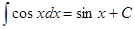
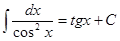
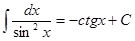
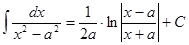
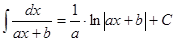
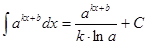
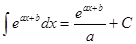 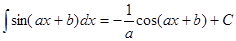 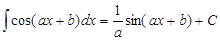
|
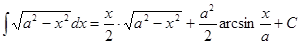
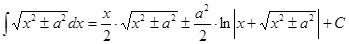
Рассмотрим нахождение интегралов непосредственным методом.
Пример 1: Найти неопределенный интеграл:
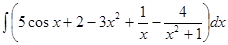 .
.
Решение: 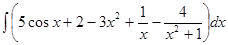 =
=
= 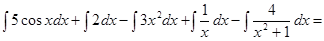
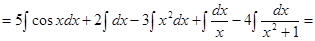

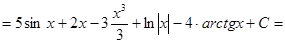
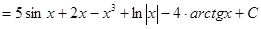 .
.
Пример 2: Найти неопределенный интеграл: 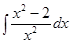 .
.
Решение: 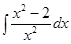 =
= 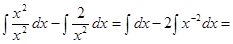

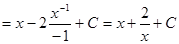 .
.
Пример 3: Найти неопределенный интеграл 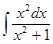
Решение: 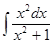 =
= 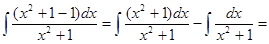
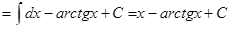
Методом замены переменной
При вычислении определенного интеграла методом замены переменной (способом подстановки) определенный интеграл 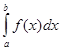 преобразуется с помощью подстановки
преобразуется с помощью подстановки 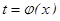 или
или 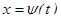 в определенный интеграл относительно новой переменной t. При этом старые пределы интегрирования a и b заменяются соответственно новыми пределами t1 и t2, которые находятся из исходной подстановки.
в определенный интеграл относительно новой переменной t. При этом старые пределы интегрирования a и b заменяются соответственно новыми пределами t1 и t2, которые находятся из исходной подстановки.
Из первой подстановки новые пределы интегрирования вычисляются непосредственно: 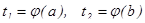 .
.
Из второй подстановки новые пределы интегрирования находятся путем решения уравнений 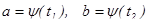 .
.
Таким образом, имеем
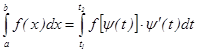
Пример 1: Вычислить определенный интеграл методом замены переменной 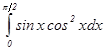
Решение: 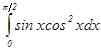 =
= 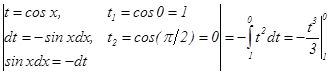
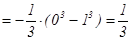 .
.
Пример 2: Вычислить определенный интеграл: 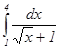 .
.
Решение: 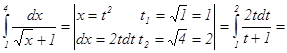
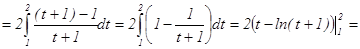
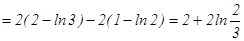 .
.
Пример.
Вычислить площадь области, ограниченной кривыми 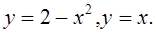
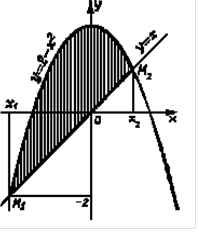
Р е ш е н и е.
Определим точки пересечения данных кривых. В точке пересечения ординаты равны, т. е. 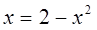 , отсюда
, отсюда 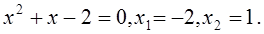 Мы получили две точки пересечения
Мы получили две точки пересечения 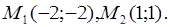
Следовательно, искомая площадь
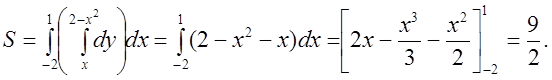 (ед2)
(ед2)
ЗАДАНИЯ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ
Вариант 1:
Найти неопределенные интегралы и вычислить определенный интеграл:
а) 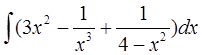 б)
б) 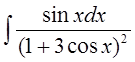 в)
в) 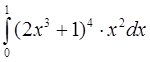
 Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж.
Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж.
Вариант 2:
Найти неопределенные интегралы и вычислить определенный интеграл:
а) 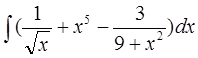 б)
б) 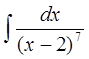 в)
в) 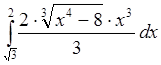
Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж.

Вариант 3:
Найти неопределенные интегралы и вычислить определенный интеграл:
а) 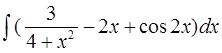 б)
б) 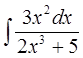 в)
в) 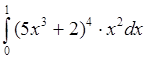
Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж.
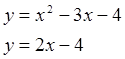
Вариант 4:
Найти неопределенные интегралы и вычислить определенный интеграл:
а) 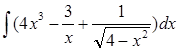 б)
б) 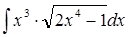 в)
в) 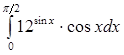
Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж.
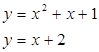
Вариант 5:
Найти неопределенные интегралы и вычислить определенный интеграл:
а) 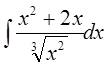 б)
б) 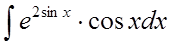 в)
в) 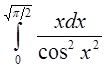
Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж.

Вариант 6:
Найти неопределенные интегралы и вычислить определенный интеграл:
а) 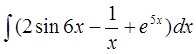 б)
б) 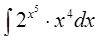 в)
в) 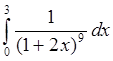
Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж.
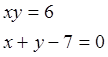
Вариант 7:
Найти неопределенные интегралы и вычислить определенный интеграл:
а) 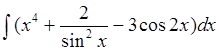 б)
б) 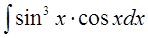 в)
в) 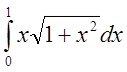
Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж. 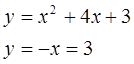
Вариант 8:
Найти неопределенные интегралы и вычислить определенный интеграл:
а) 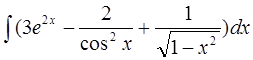 б)
б) 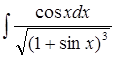 в)
в) 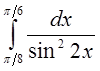
Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж.

Вариант 9:
Найти неопределенные интегралы и вычислить определенный интеграл:
а) 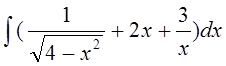 б)
б) 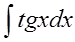 в)
в) 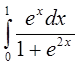
Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж.
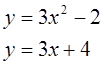
Вариант 10:
Найти неопределенные интегралы и вычислить определенный интеграл:
а) 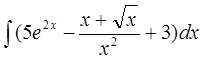 б)
б) 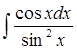 в)
в) 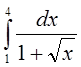
Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж.

ТЕМА 5. ТЕОРИЯ ПРЕДЕЛОВ
| Предел функции в точке | знать: определение предела, свойства пределов уметь: вычислять пределы функции |
| Второй замечательный предел | знать: второй замечательный предел уметь: использовать второй замечательный предел при вычислении пределов |
| Способы задания числовых последовательностей | знать: способы задания числовых последовательностей уметь: вычислять члены последовательности |
| Раскрытие неопределенности вида «бесконечность на бесконечность» | знать: способы раскрытия неопределенностей вида «бесконечность на бесконечность» уметь: вычислять пределы, имеющие неопределенности вида «бесконечность на бесконечность» |
| Раскрытие неопределенности вида «ноль на ноль» | знать: способы раскрытия неопределенностей вида «ноль на ноль» уметь: вычислять пределы, имеющие неопределенности вида «ноль на ноль» |
| Первый замечательный предел | знать: первый замечательный предел уметь: использовать первый замечательный предел при вычислении пределов |
ЗАДАНИЯ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ
Вариант 1.
Вычислить пределы функции y = f ( x ), при указанном поведении аргумента x.
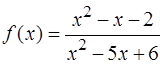 ;
;
а) 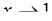 ; б )
; б ) 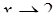 ; в)
; в) 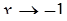 ; г)
; г) 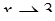 ; д)
; д) 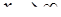 .
.
Вариант 2.
Вычислить пределы функции y = f ( x ), при указанном поведении аргумента x.
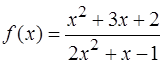 ;
;
а) 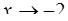 ; б )
; б ) 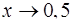 ; в)
; в) 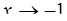 ; г)
; г) 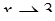 ; д)
; д) 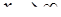 .
.
Вариант 3.
Вычислить пределы функции y = f ( x ), при указанном поведении аргумента x.
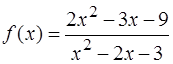 ;
;
а) 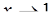 ; б)
; б) 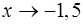 ; в)
; в) 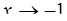 ; г)
; г) 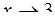 ; д)
; д) 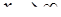 .
.
Вариант 4.
Вычислить пределы функции y = f ( x ), при указанном поведении аргумента x.
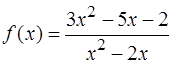 ;
;
а) 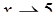 ; б)
; б) 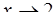 ; в)
; в) 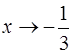 ; г)
; г) 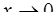 ; д)
; д) 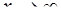 .
.
Вариант 5.
Вычислить пределы функции y = f ( x ), при указанном поведении аргумента x.
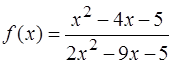 ;
;
а) 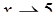 ; б)
; б) 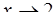 ; в)
; в) 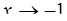 ; г)
; г) 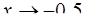 ; д)
; д) 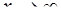 .
.
Вариант 6.
Вычислить пределы функции y = f ( x ), при указанном поведении аргумента x.
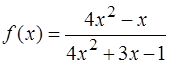 ;
;
а) 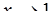 ; б)
; б) 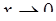 ; в)
; в) 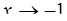 ; г)
; г) 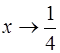 ; д)
; д) 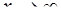 .
.
Вариант 7.
Вычислить пределы функции y = f ( x ), при указанном поведении аргумента x.
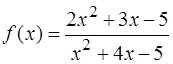 ;
;
а) 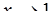 ; б)
; б) 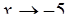 ; в)
; в) 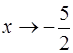 ; г)
; г) 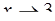 ; д)
; д) 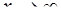 .
.
Вариант 8.
Вычислить пределы функции y = f ( x ), при указанном поведении аргумента x.
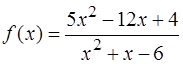 ;
;
а) 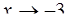 ; б)
; б) 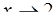 ; в)
; в) 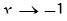 ; г)
; г) 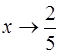 ; д)
; д) 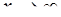 .
.
Вариант 9.
Вычислить пределы функции y = f ( x ), при указанном поведении аргумента x.
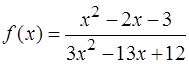 ;
;
а) 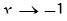 ; б)
; б) 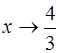 ; в)
; в) 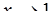 ; г)
; г) 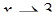 ; д)
; д) 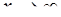 .
.
Вариант 10.
Вычислить пределы функции y = f ( x ), при указанном поведении аргумента x.
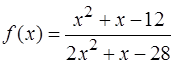 ;
;
а) 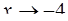 ; б)
; б) 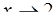 ; в)
; в) 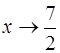 ; г)
; г) 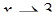 ; д)
; д) 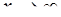 .
.
ПРИМЕРЫ РЕШЕНИЙ
Задача. Вычислить пределы функции 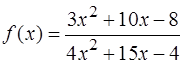 при
при
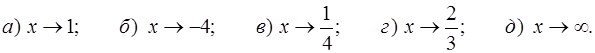
Решение. В задаче следует найти предел частного. С этой целью необходимо вычислить пределы числителя и знаменателя дроби, подставив в них предельное значение аргумента.
а) 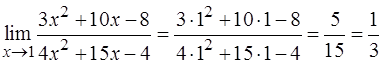 .
.
Здесь применима теорема о пределе частного.
б) 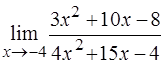 .
.
При подстановке 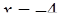 в числитель и знаменатель дроби убеждаемся, что их значения равны нулю, поэтому теорема о пределе частного здесь не применима. В данном случае говорят, что имеется неопределенность вида
в числитель и знаменатель дроби убеждаемся, что их значения равны нулю, поэтому теорема о пределе частного здесь не применима. В данном случае говорят, что имеется неопределенность вида 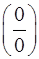 .
.
Неопределенность вида 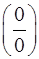 при
при 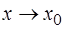 может быть раскрыта сокращением дроби на множитель вида(х–х0), который обращает числитель и знаменатель дроби в нуль, в данном случае на(х+4). Поэтому, следует разложить на множители числитель и знаменатель дроби (п.2 и п.3 прил.1).
может быть раскрыта сокращением дроби на множитель вида(х–х0), который обращает числитель и знаменатель дроби в нуль, в данном случае на(х+4). Поэтому, следует разложить на множители числитель и знаменатель дроби (п.2 и п.3 прил.1).
| 3х2+10х – 8 = 0; | 4х2+15х– 4 = 0; |
D= 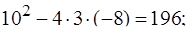
| D= 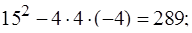
|
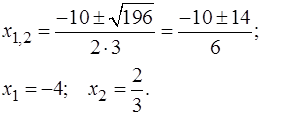
| 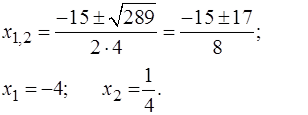
|
| 3х2+10х–8 = 3(х+4)(х–2/3) = | 4х2+15х – 4 = 4(х+4)(х–1/4 ) = |
| = (х+4)(3х–2). | = (х+4)(4х–1). |
Таким образом,
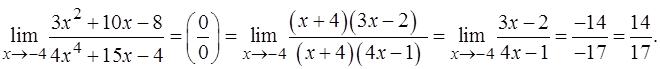
в ) 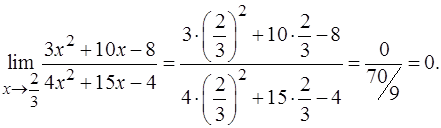
Здесь применима теорема о пределе частного, так как существуют конечные пределы числителя и знаменателя, и предел знаменателя не равен нулю.
г ) 
Здесь использована теорема о связи бесконечно малой и бесконечно большой функций.
д ) 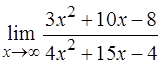 .
.
Пределы числителя и знаменателя дроби равны 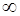 . В этом случае говорят, что имеется неопределенность вида «бесконечность на бесконечность». Теорема о пределе частного здесь не применима.
. В этом случае говорят, что имеется неопределенность вида «бесконечность на бесконечность». Теорема о пределе частного здесь не применима.
Чтобы раскрыть неопределенность вида 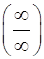 при
при 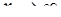 , каждый член числителя и знаменателя дроби делят на x в наивысшей степени (в нашем примере на х2), отчего величина дроби не изменится, но исчезнет неопределенность.
, каждый член числителя и знаменателя дроби делят на x в наивысшей степени (в нашем примере на х2), отчего величина дроби не изменится, но исчезнет неопределенность.
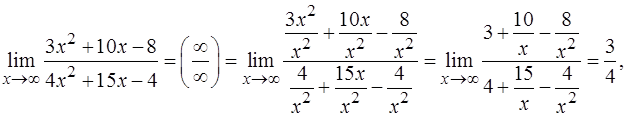
так как 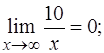
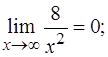
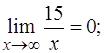
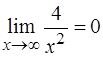
(по теореме о связи бесконечно большой и бесконечно малой функций).
Замечание. Полезно запомнить, что при 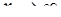 предел отношения многочленов c одинаковыми наивысшими степенями равен отношению коэффициентов при этих степенях.
предел отношения многочленов c одинаковыми наивысшими степенями равен отношению коэффициентов при этих степенях.
В нашем примере, коэффициенты при наивысшей степени х2многочленов равны 3 и 4, поэтому и предел дроби равен 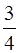 .
.
Ответы. 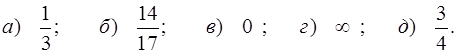
Теоретический материал
Определение: Уравнение, связывающее независимую переменную, неизвестную функцию и ее производные или дифференциалы различных порядков, называется дифференциальным уравнением.
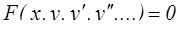 .
.
Определение:Порядком дифференциального уравнения называется порядок старшей производной, входящей в это уравнение.
(Например, y΄sinx + ytgx = 1 - первого порядка;
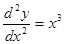 - второго порядка.
- второго порядка.
Определение: Функция y = φ ( x ), удовлетворяющая дифференциальному уравнению, называется решением этого уравнения. Решение дифференциального уравнения, содержащее столько независимых произвольных постоянных, каков порядок уравнения, называется общим решением этого уравнения.
Для уравнения 1-го порядка: y = φ(x, C)
2-го порядка: y = φ(x, C1, C2)
Определение: Функции, получаемые из общего решения при различных числовых значениях произвольнх постоянных, называются частными решениями этого уравнения.
Определение: Задача на нахождение частного решения дифференциального уравнения при заданных начальных условиях называется задачей Коши.
Первого порядка
Определение: Однородной функцией переменных x и y называется функция, все члены которой имеют одинаковую степень.
Например, 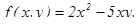
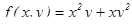 - однородные функции второй и третьей степени соответственно.
- однородные функции второй и третьей степени соответственно.
Определение: Уравнение вида 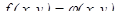 , где
, где 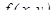 и
и 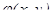 - однородные функции одной и той же степени, называетсяоднородным дифференциальным уравнением первого порядка.
- однородные функции одной и той же степени, называетсяоднородным дифференциальным уравнением первого порядка.
Однородное уравнение приводится к уравнению с разделяющими переменными подстановкой, где 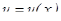 – новая искомая функция.
– новая искомая функция.
Пример 1: Найти общее решение уравнения
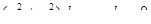 .
.
Решение: Положим 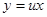 . Дифференцируя равенство y = ux, получим
. Дифференцируя равенство y = ux, получим 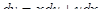 . Подставляя выражения в уравнение, получим:
. Подставляя выражения в уравнение, получим: 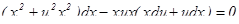
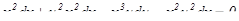
Разделим переменные в полученном уравнении.
 ;
; 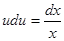
Интегрируем, 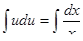 . Отсюда,
. Отсюда, 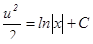 .
.
Сделаем обратную замену: 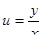 , получим
, получим 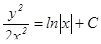 .
.
Ответ: 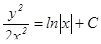 .
.
Первого порядка
Определение: Уравнение вида 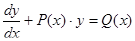 называется линейным дифференциальным уравнением первого порядка.
называется линейным дифференциальным уравнением первого порядка.
Уравнения такого вида сводятся к двум уравнениям с разделяющимися переменными с помощью подстановки 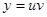 , где
, где 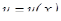 ,
, 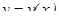 - некоторые функции, зависящие от x.
- некоторые функции, зависящие от x.
Алгоритм решения:
1) Вводится подстановка 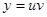 , тогда
, тогда 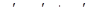 .
.
2) Исходное уравнение принимает вид:
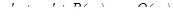 .
.
3) Группируются слагаемые при u.
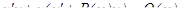 .
.
4) Выражение в скобках приравнивается к нулю:
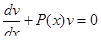 .
.
Это уравнение с разделяющимися переменными, решая его, находим 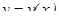 .
.
5) Полученное значение v подставляется в выражение:
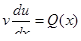 .
.
Решив уравнение с разделяющимися переменными, получим функцию 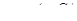 .
.
6) Общее решение уравнения запишется в виде:
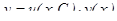 .
.
Пример 1: Найти общее решение уравнения
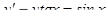 .
.
Решение: Обозначим 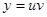 , тогда
, тогда 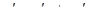 .
.
Уравнение примет вид  .
.
Вынесем во втором и третьем слагаемом общий множитель за скобки, получим 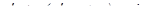 .
.
Выражение в скобках приравняем к нулюv ′ - vtgx = 0
Перепишем в виде 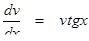
Умножая обе части уравнения на 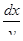 , получим
, получим 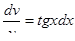 ,
,
интегрируем 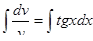
находим 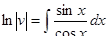 , применим замену
, применим замену 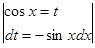
получим 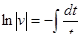 ,
,
откуда 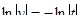 или
или 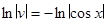 ,
, 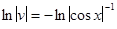 .
.
Пропотенцируем обе части равенстваv = 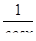 .
.
Найденную функцию 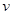 подставим в выражение
подставим в выражение 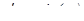 и решим полученное уравнение
и решим полученное уравнение 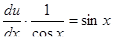
du = sinx ∙ cos ∙ xdxили 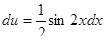
Интегрируем 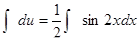 ,
,
Получим 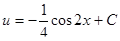 .
.
Зная функции u и v , можно записать ответ.
Ответ: Общее решение уравнения у = 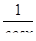
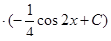 .
.
Пример 2: Найти частное решение дифференциального уравнения 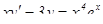 , если
, если 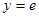 при
при 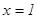 .
.
Решение: Пусть 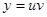 , тогда
, тогда 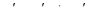 .
.
Отсюда,  .
.
Вынесем u за скобки: 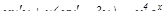 .
.
Приравняв скобку к 0 , получим: 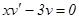 .
.
Отсюда, 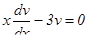 ,
, 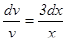 .
.
Интегрируем 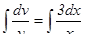 ,
,
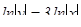 ,
, 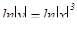 ,
,  .
.
Подставив  в выражение
в выражение  , получим уравнение относительно функции u и решим его.
, получим уравнение относительно функции u и решим его.
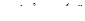 ,
, 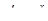 ,
, 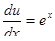 , .
, .
Проинтегрируем 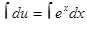 . Функция
. Функция  .
.
Запишем общее решение уравнения : 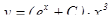 .
.
Частное решение найдем из условия 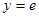 при
при 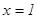 .
.
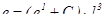 ,
, 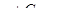 ,
, 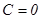 .
.
Частное решение заданного уравнения имеет вид: 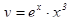 .
.
Ответ: 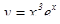 - частное решение уравнения.
- частное решение уравнения.
Линейные однородные
Определение.Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида
y″ + py′ + qy = f ( x ),
где p и q – постоянные величины, а f(x) – непрерывная функция x.
Если правая часть уравнения равна нулю, т.е.
y″ + py′ + qy = 0,
то оно называется однородным уравнением.
Для практического использования алгоритм решениядифференциальных уравнений второго порядка с постоянными коэффициентамиудобно оформить в виде таблицы:
| Дифференциальное уравнение |
y″ + py′ + qy = 0 | ||
| Характеристическое уравнение |
k2 + pk + q = 0
| ||
| Дискриминант D = p2 – 4q | D > 0 | D = 0 | D < 0 |
| Корни характеристического уравнения | k1 ≠ k2 | k1 = k2 | k1 = a + bi k2 = a - bi |
| Множества решений |
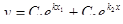
|
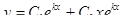
|

|
Пример.Решить уравнение y″ + 2y′ – 8y = 0.
Решение.
Составим характеристическое уравнение k2 + 2k - 8 = 0.
Найдем дискриминант D = p2 – 4q = 22 -4(-8) = 4 + 32 = 36 > 0.
Следовательно, характеристическое уравнение имеет два различных действительных корня. Определим их: k1 = - 4, k2 = 2.
Находим частные решения данного дифференциального уравнения:
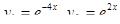 .
.
Общее решение данного уравнения имеет вид
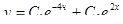 .
.
ЗАДАНИЯ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ
Вариант 1
Найти общее решение дифференциального уравнения
1. y′ = 6x3;
2. y′′ + y′ – 6y = 0
3. 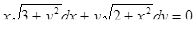 4.
4. 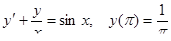 5.
5. 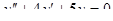
|
Вариант 2
Найти общее решение дифференциального уравнения
1. y′ = 8x2 ;
2. y′′ – 6y + 9 = 0
3. 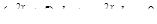 4.
4. 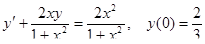 5.
5. 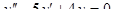
|
Вариант 3
Найти общее решение дифференциального уравнения
1. y′ = 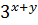 ;
2. y′′ – 2y′ – 8y = 0.
3. ;
2. y′′ – 2y′ – 8y = 0.
3.  4.
4. 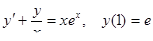 5.
5. 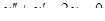
|
Вариант 4
Найти общее решение дифференциального уравнения
1. yy′ + x = 0;
2. y′′ – 8y + 16 = 0
3. 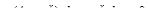 4.
4. 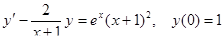 5.
5. 
|
Вариант 5
Найти общее решение дифференциального уравнения
1. 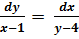 ;
2. ;
2. 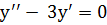 3.
3. 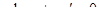 4.
4. 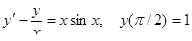 5.
5. 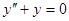
|
Вариант 6
Найти общее решение дифференциального уравнения
1. y′ = 5x;
2. y′′ – 3y′ + 2y = 0
3. 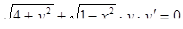 4.
4. 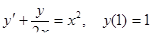 5.
5. 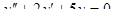
|
Вариант 7
Найти общее решение дифференциального уравнения
1. y′ = x2 + x;
2. y′’ + 4y = 0
3. 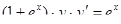 4.
4. 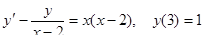 5.
5. 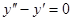
|
Вариант 8
Найти общее решение дифференциального уравнения
1. y′ = x3 + 1;
2. y′′ – 8y + 15y = 0
3. 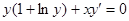 4.
4.  5.
5. 
|
Вариант 9
Найти общее решение дифференциального уравнения
1. y′ = 8x3;
2. y′′ – 6y′ + 5y = 0;
3. 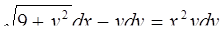 4.
4. 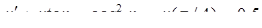 5.
5. 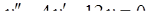
|
Вариант 10
Найти общее решение дифференциального уравнения
1. 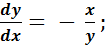 2. y′′ – 4y′ + 13y = 0.
3.
2. y′′ – 4y′ + 13y = 0.
3. 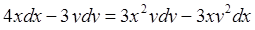 4.
4. 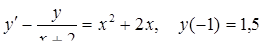 5.
5. 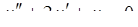
|
ТЕМА 1. КОМПЛЕКСНЫЕ ЧИСЛА. ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ В РАЗНЫХ ФОРМАХ ЗАПИСИ
| Элементы содержания | Требования к знаниям и умениям |
| Действия над комплексными числами, заданными в алгебраической форме | знать: правила выполнения действий с комплексными числами в алгебраической форме уметь: выполнять действия над комплексными числами в алгебраической форме |
| Тригонометрическая форма комплексного числа | знать: формулы перехода от алгебраической формы к тригонометрической форме комплексного числа; правила выполнения действий над комплексными числами, заданными в тригонометрической форме уметь: находить тригонометрическую форму комплексного числа; выполнять действия над комплексными числами, заданными в тригонометрической форме |
| Решение уравнений | знать: определение комплексного числа уметь: находить корни квадратного уравнения с отрицательным дискриминантом |
| Сопряженные комплексные числа | знать: понятие сопряженных комплексных чисел уметь: записывать число, сопряженное заданному комплексному числу |
| Модуль комплексного числа | знать: понятие модуля комплексного числа уметь: вычислять модуль комплексного числа |
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ:
1. Определение комплексного числа.
Число 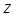 вида
вида 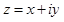 , где
, где 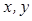 - любые действительные числа, а
- любые действительные числа, а 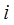 - так называемая мнимая единица, называется комплексным числом.
- так называемая мнимая единица, называется комплексным числом.
 или
или 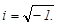
Действительные числа x и y называются соответственно действительной и мнимой частями комплексного числа z и обозначаются 
Рассмотрим частные случаи комплексных чисел.
· Пусть y=0, x- любое действительное число. Тогда 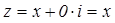 становится действительным числом.
становится действительным числом.
· Пусть 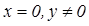 . Тогда
. Тогда 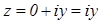 - чисто мнимое число.
- чисто мнимое число.
Таким образом, все действительные числа и все чисто мнимые числа входят в множество комплексных чисел.
Два комплексных числа 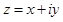 и
и 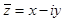 называются сопряженнымикомплексными числами.
называются сопряженнымикомплексными числами.
Сравнение комплексных чисел осуществляется по правилам:
1. Два комплексных числа 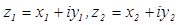 считаются равными, если
считаются равными, если 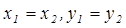 .
.
2. Комплексное число 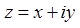 равно нулю только тогда, когда
равно нулю только тогда, когда 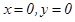 одновременно.
одновременно.
3. Операции <, > не имеют смысла на множестве комплексных чисел.
2. Геометрическое изображение комплексных чисел.
Рассмотрим декартову прямоугольную систему координат ХОУ на плоскости. Каждой точке плоскости при этом соответствуют вполне определенные координаты 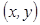 , а следовательно, и вполне определенное комплексное число
, а следовательно, и вполне определенное комплексное число 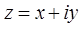 . Обратно, каждому к
. Обратно, каждому к 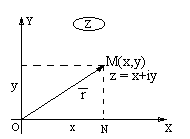 омплексному числу
омплексному числу 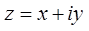 соответствует вполне определенная пара действительных чисел
соответствует вполне определенная пара действительных чисел 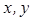 , а следовательно, и вполне определенная точка плоскости
, а следовательно, и вполне определенная точка плоскости 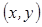 . Таким образом установили связь между множеством точек на плоскости и множеством комплексных чисел. Плоскость, точки которой изображают комплексные числа
. Таким образом установили связь между множеством точек на плоскости и множеством комплексных чисел. Плоскость, точки которой изображают комплексные числа 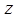 , называется комплексной плоскостью. Ось ОХ называется действительной осью, ось ОУ – мнимой осью. Очевидно, что изображением комплексного числа
, называется комплексной плоскостью. Ось ОХ называется действительной осью, ось ОУ – мнимой осью. Очевидно, что изображением комплексного числа 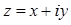 можно считать также и вектор
можно считать также и вектор 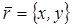 .
.
3. Тригонометрическая форма записи комплексного числа.
Длина вектора, изображающего комплексное число 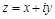 ,
, 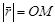 называется модулем комплексного числа.
называется модулем комплексного числа.
Угол j, образуемый этим вектором с положительным направлением действительной оси (ÐMON) , называется аргументом комплексного числа.
Обозначение: модуль 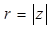 ,
,
аргумент 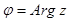 .
.
Из прямоугольного треугольника OMN

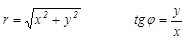 .
.
В качестве главного значения аргумента комплексного числа обычно выбирают значение 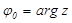 , определенное неравенствами
, определенное неравенствами
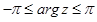 ,
,
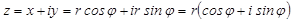 .
.
Итак, 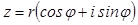 называется тригонометрической формойзаписи комплексногочисла.
называется тригонометрической формойзаписи комплексногочисла.
Пример.Записать в тригонометрической форме комплексные числа:
1. 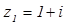
2. 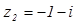
3. 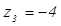
4. 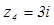 .
.
Решение:
1. 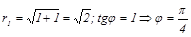
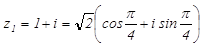 .
.
2. 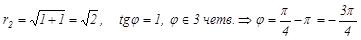 .
.
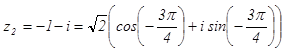 .
.
3. 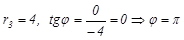
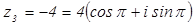 .
.
4. 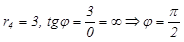
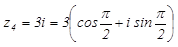 .
.
4. Действия над комплексными числами.
1. Сложение.
Суммой двух комплексных чисел 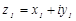 и
и 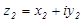 называется комплексное число
называется комплексное число 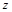 , определяемое равенством
, определяемое равенством
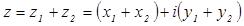 .
.
Из определения вытекают следующие законы сложения:
- Переместительный : 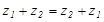
- Сочетательный: 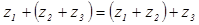
2. Вычитание.
Вычитание комплексных чисел определяется как действие, обратное сложению. Вычесть из числа 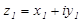 число
число 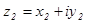 значит найти такое число
значит найти такое число 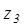 , чтобы имело место равенство:
, чтобы имело место равенство: 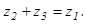 Число
Число 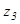 называется разностью чисел
называется разностью чисел 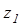 и
и 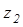 и обозначается
и обозначается 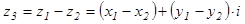 .
.
Вычитаниевсегдавыполнимо.
3. Умножение.
Произведением 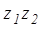 двух комплексных чисел
двух комплексных чисел 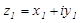 и
и 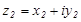 называется комплексное число, определяемое равенством
называется комплексное число, определяемое равенством 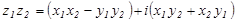 .
.
Из определения следуют законы:
· Переместительный 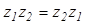
· Сочетательный 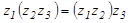
· Распределительный 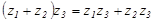 .
.
4. Деление.
Деление – действие, обратное умножению. Разделить комплексное число 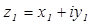 на комплексное число
на комплексное число 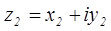 значит найти такое число
значит найти такое число 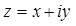 , чтобы имело место равенство
, чтобы имело место равенство 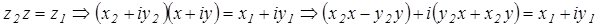 .
.
Тогда получаем систему для определения 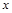 и
и 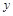 :
:
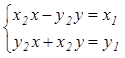
Система всегда разрешима, т.к. определитель
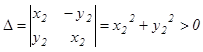 .
.
Число 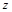 называется частным.
называется частным.
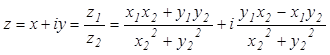 .
.
Итак, чтобы разделить одно комплексное число на другое, надо числитель и знаменатель дроби умножить на комплексное число, сопряженное числу, стоящему в знаменателе.
5. Умножение и деление комплексных чисел, заданных в тригонометрической форме.
Пусть 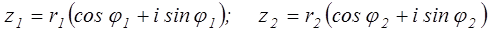 .
.
Тогда 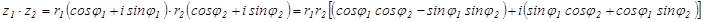
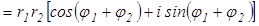 .
.
Следовательно, при умножении комплексных чисел их модули умножаются , а аргументы складываются: 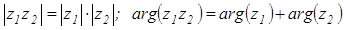 .
.
Деление комплексных чисел, записанных в тригонометрической форме, приводит к формуле:
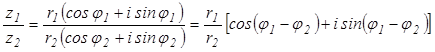 .
.
ЗАДАНИЯ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ:
Вариант 1
1. Решить квадратное уравнение:
х2 + 2х + 5 = 0.
2. Найти действительные числа x и y из условия равенства двух комплексных чисел
5х – 2у + (х + у)i = 4 + 5i .
3. Выполнить действия:
a. 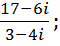
b. (1 - i)3;
c. i40 – i21.
4. Выполнить действия и записать результат в тригонометрической форме:
a. 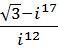
b. 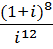
5. Изобразить решения, полученные в пункте 4, на комплексной плоскости
Вариант 2
1. Решить квадратное уравнение:
х2 + 2х + 4 = 0.
2. Найти действительные числа x и y из условия равенства двух комплексных чисел
5х i – 2+ 4у = 9i + 2x + 3yi .
3. Выполнить действия:
a. 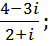
b. (1 + i)3;
c. i3 – i100.
4. Выполнить действия и записать результат в тригонометрической форме:
a. 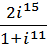
b. 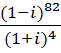
5. Изобразить решения, полученные в пункте 4, на комплексной плоскости
Вариант 3
1. Решить квадратное уравнение:
х2-6х + 18 = 0.
2. Найти действительные числа x и y из условия равенства двух комплексных чисел
9 + 2х i+4у i= 10i + 5x – 6y .
3. Выполнить действия:
a. 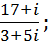
b. (1 - i)4;
c. i13 – i33.
4. Выполнить действия и записать результат в тригонометрической форме:
a. 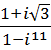
b. 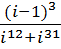
5. Изобразить решения, полученные в пункте 4, на комплексной плоскости
Вариант 4
1. Решить квадратное уравнение:
х2-4х + 5 = 0.
2. Найти действительные числа x и y из условия равенства двух комплексных чисел
2х i+3у i+ 17 = 3x + 2y + 18i .
3. Выполнить действия:
a. 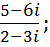
b. (1 - i)4;
c. i17 – i38.
4. Выполнить действия и записать результат в тригонометрической форме:
a. 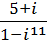
b. 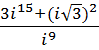
5. Изобразить решения, полученные в пункте 4, на комплексной плоскости
Вариант 5
1. Решить квадратное уравнение:
х2 + 6х + 10 = 0.
2. Найти действительные числа x и y из условия равенства двух комплексных чисел
4х+5у – 9 + 7 (3х-у)i = 10x + 14yi .
3. Выполнить действия:
a. 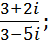
b. (3 - 4i)3;
c. i15 – i37.
4. Выполнить действия и записать результат в тригонометрической форме:
a. 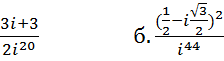
5. Изобразить решения, полученные в пункте 4, на комплексной плоскости
Вариант 6
1. Решить квадратное уравнение:
х2-10х + 41 = 0.
2. Найти действительные числа x и y из условия равенства двух комплексных чисел
3 + 4х i+5у i=12i + 5x – 2y .
3. Выполнить действия:
a. 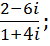
b. (2 + 5i)3;
c. i23 – i111.
4. Выполнить действия и записать результат в тригонометрической форме:
a. 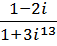
b. 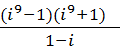
5. Изобразить решения, полученные в пункте 4, на комплексной плоскости
Вариант 7
1. Решить квадратное уравнение:
2х2- 2х + 5 = 0.
2. Найти действительные числа x и y из условия равенства двух комплексных чисел
х(2 + i) –у (1-i ) = 1 + 3i .
3. Выполнить действия:
a. 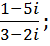
b. (1 + 7i)3;
c. i45 – i11.
4. Выполнить действия и записать результат в тригонометрической форме:
a. 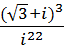
b. 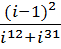
5. Изобразить решения, полученные в пункте 4, на комплексной плоскости
Вариант 8
1. Решить квадратное уравнение:
25х2- 20х + 13 = 0.
2. Найти действительные числа x и y из условия равенства двух комплексных чисел
х(1 + i) + y(2 – 3i) = 3i + 1.
3. Выполнить действия:
a. 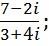
b. (1 - 5i)3;
c. i58 – i51.
4. Выполнить действия и записать результат в тригонометрической форме:
a. 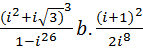
5. Изобразить решения, полученные в пункте 4, на комплексной плоскости
Вариант 9
1. Решить квадратное уравнение:
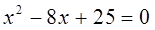 .
.
2. Найти действительные числа x и y из условия равенства двух комплексных чисел
9 + 2ix+4iy = 10i+5x-6y .
3. Выполнить действия:
a. 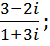
b. (3 - 2i)3;
c. i15 – i57.
4. Выполнить действия и записать результат в тригонометрической форме:
a. 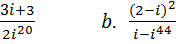
5. Изобразить решения, полученные в пункте 4, на комплексной плоскости
Вариант 10
1. Решить квадратное уравнение:
х2-6х + 18 = 0.
2. Найти действительные числа x и y из условия равенства двух комплексных чисел
2х i+3у i+ 17= 3x + 2y + 18 .
3. Выполнить действия:
a. 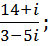
b. (1 - 2i)4;
c. i23 – i35.
4. Выполнить действия и записать результат в тригонометрической форме:
a. 
5. Изобразить решения, полученные в пункте 4, на комплексной плоскости.
ПРИМЕРЫ РЕШЕНИЙ
1. Решите во множестве комплексных чисел уравнение 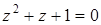 .
.
Решение:
Так как 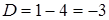 , тогда корни находятся по формуле
, тогда корни находятся по формуле 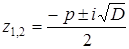
( 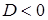 ).
).
Отсюда, 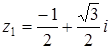 ,
, 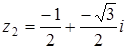 .
.
Ответ: 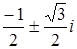 .
.
.
Решите уравнение 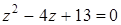
Решение:
По формуле 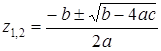 , находим:
, находим:
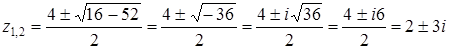 .
.
2. При каких действительных значениях x и y комплексные числа 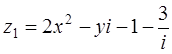 и
и 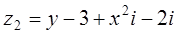 будут равными?
будут равными?
Решение:
Комплексные числа 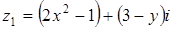 и
и 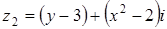 будут равными, если выполняются условия:
будут равными, если выполняются условия:
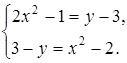
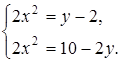
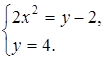
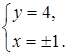
Ответ: 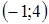 ;
; 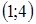 .
.
3. Вычислите 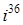 ;
; 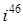 ;
; 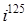 ;
; 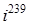 .
.
Решение:
С помощью формулы: 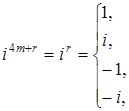
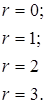
легко получаем:
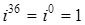 ;
;
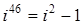 ;
;
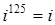 ;
;
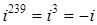 .
.
Ответ: 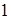 ;
; 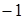 ;
; 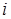 ;
; 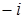 .
.
4. Выполнить все действия над комплексными числами 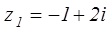 и
и 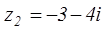 .
.
Решение
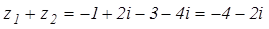
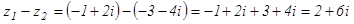
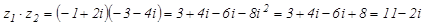
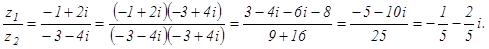
5. Выполните указанные действия: 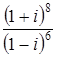 .
.
Решение
Вычислим значение дроби 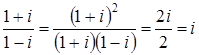 .
.
Следовательно, 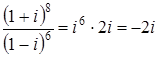
Ответ: 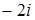 .
.
6. Изобразите на комплексной плоскости следующие комплексные числа:
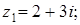
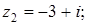
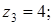
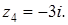
Решение
Данным комплексным числам соответствуют точки комплексной плоскости.
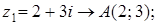
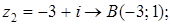
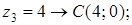
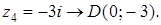
Покажем их.

7. Запишите комплексные числа в тригонометрической форме:
а) 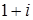 ; б)
; б) 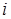 ; в)
; в) 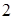 ; г)
; г) 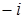 ; д)
; д) 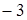 ; е)
; е) 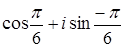 ; ж)
; ж) 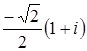 .
.
Решение
Так как тригонометрическая форма комплексного числа имеет вид 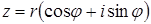 , тогда:
, тогда:
а) В комплексном числе 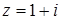 :
: 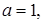
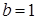 .
.
Тогда 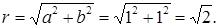
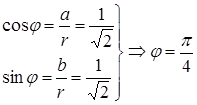 ,
,
Поэтому 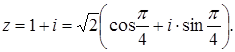
б) 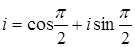 , где
, где 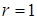 ,
, 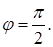
в) 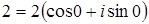 , где
, где 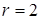 ,
, 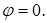
г) 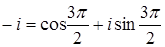 , где
, где 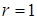 ,
, 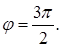
д) 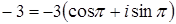 , где
, где 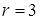 ,
, 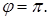
е) 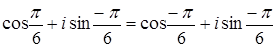 .
.
ж) 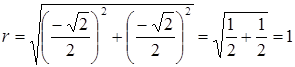 , а
, а 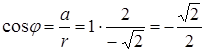 , то
, то 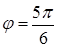 .
.
Поэтому 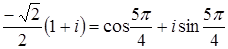
Ответ: 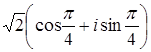 ;
; 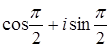 4;
4; 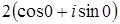 ;
; 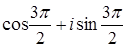 ;
; 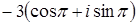 ;
; 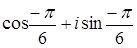 ;
; 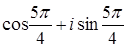 .
.
Дата: 2018-11-18, просмотров: 432.